Question 1.
What path will the moon take when the gravitational interaction between the moon and earth disappears? (AS 2)
Answer:
The force of attraction between moon and earth is given by F =GMm/R2
M = mass of the earth ; m = mass of the moon ; R = radius of the earth
Here the gravitational interaction between moon and earth disappears.
∴ G = 0 ⇒ F = 0
- Therefore the moon neither revolves around the earth nor fall into the earth.
- It takes a straight path away from the earth.
Question 2.
A Car moves with constant speed of 10 m/s in a circular path of radius 10 m. The mass of the car is 1000kg. Who or what is providing the required centripetal force for the car? How much is it? (AS 1)
Answer:
Speed of the car (v) = 10 m/s ; Radius of the path (r) = 10 m
Weight of the car (m) = 1000kg
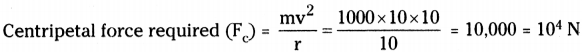
The required centripetal force is provided by the friction between the tyres of the car and the road.
Question 3.
A small metal washer is placed on the top of a hemisphere of radius R. What minimum horizontal velocity should be imparted to the washer to detach it from the hemisphere at the initial point of motion? (AS 1, AS 7)
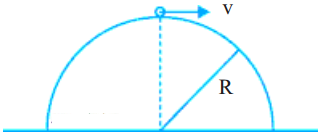
Answer:
Radius of hemisphere = R; Mass of hemisphere = M
Let the radius of washer = r and mass = m
Distance between hemisphere and washer = R + r
The centripetal force required to rotate the washer =mv2/r
The gravitational force of washer due to hemisphere is =GMm/R2
But the necessary centripetal force must be equal to the gravitational force

Question 4.
Explain why a long pole is more beneficial to the tight rope walker if the pole has slight bending. (AS 1, AS 7)
Answer:
- You must have noticed the circus artists doing rope walking.
- During this act, they carry a long bamboo pole in their hands.
- The reason for this is that the line joining the centre of gravity and centre of equilibrium must fall within the rope for achieving the stable equilibrium.
- Thus when an artist finds that he is falling towards left, he shifts bamboo pole towards right, so that his centre of gravity stay undisturbed.
- Thus he can balance himself on the rope.
Question 5.
Why is it easier to carry the same amount of water in two buckets, one in each hand rather than in a single bucket? (AS 7)
Answer:
It is because in the later case centre of gravity of our body shifts towards the bucket and there is a tendency that the line joining the centre of gravity and centre of equilibrium may fall outside our feet.
However in the former case the centre of gravity not only gets lowered, but also it is at such a point that line joining the C.G. and C.E. falls within our feet.
Hence one is a stable equilibrium.
Question 6.
What is the speed of an apple dropped from a tree after 1.5 second? What distance will it cover during this time? Take g = 10 m/s2. (AS 1)
Answer:
An apple is dropped from a tree.
∴ Initial velocity u = 0 ; Time t = 1.5 s
a = g = 10 m/s2 ; Final velocity v = ?
v = u + at = 0 + 10 x 1.5 = 0 + 15 = 15 m/s
Distance covered (s) = ut + 1/2 at2 = 0 × 1.5 + 1/2 × 10 × 1.5 × 1.5 = 0 + 5 × 2.25 = 11.25 m
Question 7.
A body is projected with a speed of 40 m/s vertically up from the ground. What is the maximum height reached by the body? What is the entrie time of motion? What is the velocity at 5 seconds after the projection? Take g = 10 m/s2 . (AS 1)
Answer:
Initial speed u = 40 m/s ; g = 10 m/s2
Maximum height reached (h) = u2/2 g=40×40/2×10 = 80 m
Entire time of motion (T) = 2u/g=2×40/10 = 8 s
Entire time of motion is 8 seconds.
∴ It starts to fall down after 4 seconds.
At 5 seconds the body is in downward direction.
u = 0 m/s, a = g = 10 m/s2, t = 5 - 4 = 1 sec.
v = u + at = 0 + 10 × 1 = 10 m/s
∴ The velocity at 5 seconds is 10 m/s downward.
Question 8.
A boy is throwing balls into the air one by one in such a way that when the first ball thrown reaches maximum height he starts to throw the second ball. He repeats this activity. To what height do the balls rise if he throws twice in a second? (AS 1, AS 7)
Answer:
The boy throws the second ball when the first ball reaches its maximum height. He throws twice in a second.
Time of ascent of first ball is 1/2 sec.
After 1/2 sec, the first ball starts to fall down and the second ball starts from ground.
Let the distance travelled = s meters.; Initial velocity = u m/s
Time of ascent (t1) = 1/2 sec.
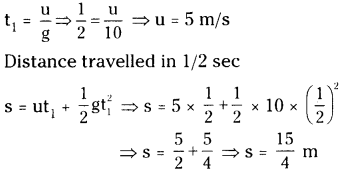
They reach a height of 15/4 meters.
Question 9.
A man is standing against a wall such that his right shoulder and right leg are in contact with the surface of the wall along his height. Can he raise his left leg at this position without moving his body away from the wall? Why? Explain. (AS 7)
Answer:
- When the right leg and right shoulder are in contact with the surface of the wall along the height of a man, his weight is towards the wall.
- The centre of gravity will be away from the foot. Just like in the case of carrying a bucket full of water with one hand.
- The line joins the centre of gravity and centre of equilibrium is not perpendicular to the horizontal.
- Hence he cannot lift his left leg without moving his body along the wall.
Question 10.
A ball is dropped from a height. If it takes 0.2 s to cross the last 6 m before hitting the ground, find the height from which it is dropped. Take g = 10 m/ s2. (AS 1)
Answer:
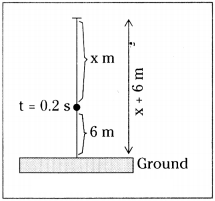
For last 6 m, distance travelled
s = 6 m ; u = ? ; t = 0.2 sec ; a = g = 10 m/s2
s = ut + 1/2 at2
6 = u (0.2) + 1/2 × 10 × (0.2)2
6 = (0.2) u + (5 × 0.04)
6 - 0.2 = 0.2 u
5.8 = 0.2 u ⇒ u = 5.8/0.2 = 29
∴ u = 29 m/s
This u will be the final velocity while travelling the distance x.
∴ s = x, v = 29 m/s, a = g = 10 m/s2, u = 0 m/s
v2 - u2 = 2as ⇒ 292 - 0 = 2 × 10 × x ⇒ x = 841/20 = 42.05 m
∴ Total distance = x + 6 = 42.05 + 6 = 48.05 m
∴ The ball is dropped from a height of 48.05 m.
Question 11.
A ball is dropped from a balloon going up at a speed of 5 m/s. If the balloon was at a height 60 m. At the time of dropping the ball, how long will the ball take to reach the ground? (AS 1, AS 7)
Answer:
At t = 0, the stone was going up with a velocity of 5 m/s. After that it moves as a freely falling body, with downward acceleration ‘g’.
If it reaches the ground at time t1,

Question 12.
A ball is projected vertically up with a speed of 50 m/s. Find the maximum height, the time to reach the maximum height, and the speed at of the maximum height. (g = 10 m/ s2) (AS 1)
Answer:
Initial speed u = 50 m/s ; g = 10 m/s2

After reaching maximum height, the velocity becomes ‘zero’.
Question 13.
Two cars having masses m1 and m2move in circles of radii r1and r2respectively. If they complete the circle in equal time. What is the ratio of their speeds and centripetal accelerations? (AS 1)
Answer:
Masses of cars : m1and m2; Radius of circles : r1and r2
Given that their time period is equal.

Question 14.
Two spherical balls of mass 10 kg each are placed with their centers 10 cm apart. Find the gravitational force of attraction between them. (AS 1)
Answer:
Masses of balls M1and M2= 10 kg each.; Distance d = 10 cm = 0.1 m
Gravitational force of attraction between them is
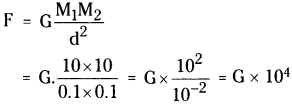
Question 15.
Find the free-fall acceleration of an object on the surface of the moon, if the radius of the moon and its mass are 1740 km and 7.4 × 1022kg respectively. Compare this value with free fall acceleration of a body on the surface of the earth. (AS 1)
Answer:
Radius of the moon = 1740 km = 1740 × 103 m
Mass of the moon = 7.4 × 1022kg ; G = 6.67 × 10-11Nm2 kg-2
Free fall acceleration of a body on the surface of the moon
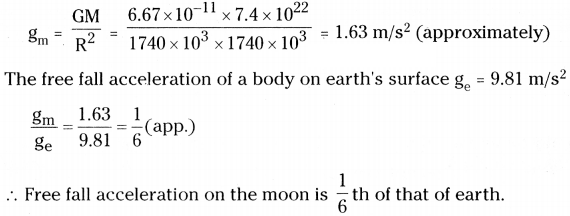
Question 16.
Can you think of two particles which do not exert gravitational force on each other? (AS 2)
Answer:
Two particles which do not exert gravitational force on each other will be mass less particles. But every particle has even a little mass. Hence we cannot find two particles which do not exert gravitational force on each other.
Question 17.
An apple falls from a tree. An insect in the apple finds that the earth is falling towards it with an acceleration g. Who exerts the force needed to accelerate the earth with this acceleration? (AS 7)
Answer:
- According to Newton’s third law, when an apple is freely falling, the force on the apple due to earth is equal to the force on the earth due to apple.
- The force is due to gravity, which causes acceleration in the body.
- As the insect is inside the freely falling apple, it feels that the earth is falling towards it with an acceleration ’g’.
- According to the insect, the acceleration is due to the force on the apple due to the earth.
- Actually the earth is not falling towards the apple.
Question 18.
A scooter weighing 150 kg together with its rider moving at 36 kin/hr is to take a turn of radius 30 in. What force on the scooter towards the center is needed to make the turn possible ? Who or what provides this? (AS 1)
Answer:
Weight of the scooter with rider = 150 kg
Speed = 36 km/hr = 36 × 518 = 10 m/sec.
Radius of the turning = 30 m
The force needed on the scooter towards the centre is centripetal force.
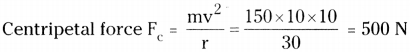
∴ A centripetal force of 500 N is required on the car.
This force is provided by the friction between the tyres of the car and road.
Question 19.
The bob of simple pendulum of length 1 m has mass 100 g and a speed of 1.4 m/s at the lowest point in its path. Find the tension in the string at this moment. (Take g = 9.8 m/sec2) (AS 1)
Answer:
Mass of the bob = 100 g = 0.1 kg ; Length of the string = 1 m
Speed of the bob v = 1.4 m/s ; Let the tension in the string be T.
The forces acting on the bob are
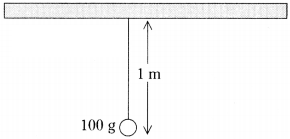
a) Weight of the bob mg, downwards
b) Tension in the string ‘T’ upward
Weight of bob =mv2/l
Tension in the string T = g cos θ
∴ According to Newton’s third law
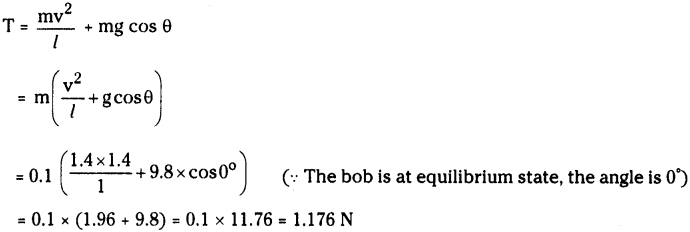
Question 20.
How can you find the centre of gravity of India map made with steel? Explain. (AS 3)
(OR)
Describe an activity to know the center of gravity of a India map.
Answer:
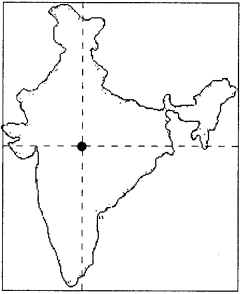
- Take an India map made of steel.
- Make holes at four different corners i.e., top, bottom, left, and right, and name them as A, B, C, and D as shown in figure.
- Suspend the map through a hole A, by means of a string to a nail ‘P’ as shown in figure.
- Suspend a plumb line from the nail P.
- Draw the line AX along the plumb line.
- Similarly suspend the map through other holes B, C and D and draw lines BY, CZ, DW along the plumb line.
- These lines (more than two) intersect at a point.
- This point (G) is the centre of gravity of the map.
Question 21.
Explain some situations where the center of gravity of man lies out side of the body. (AS 1)
Answer:
Centre of gravity of a human being is located interior to the second sacral vertebra.
Centre of gravity of man lies out side the body in the following situation :
a) While doing sit-ups.
b) While carrying a load like bucket full of water with one hand.
c) While walking on a narrow base like walking on a rope or pole or narrow wall, etc.
d) While walking with one leg.
e) As age increases its position changes.
Question 22.
Where does the centre of gravity of atmosphere of the earth lie? (AS 2)
Answer:
The earth’s atmosphere is about 10,000 km thick, but most of its bulk is contained in the first 11 km above the earth’s surface. Since the earth and its atmosphere are roughly spherical, the centre of the earth is also the centre of gravity of the earth’s atmosphere.
Question 23.
Where does the center of gravity lie, when a boy is doing sit-ups? Explain. (AS 7)
Answer:
- The centre of gravity of a boy when he start erect, falls in the foot.
- When he is doing sit-ups, the centre of gravity shifts from foot to his base.
- The weight vector also move from the base.
- Hence the boy stretches his hands or bends slightly towards the earth. While doing sit-ups, in order to make the weight vector pass through base, so that he acquire stability.