1st Lesson Real Numbers Class 10 Important Questions with Solutions
10th Class Maths Real Numbers 1 Mark Important Questions
Question 1.
Write the exponent of 2 in the prime factorization of 144.
Solution:
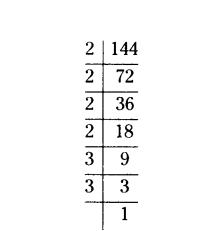
144 = 2 × 2 × 2 × 2 × 3 × 3
= 24 × 32
Therefore, exponent of 2 is 4.
Question 2.
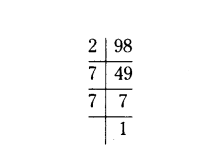
Write 98 as the product of its prime factors.
Solution:
98 = 2 × 7 × 7
Question 3.
State the Euclid’s Division Lemma.
Solution:
Let a and b are any two positive integers, then there exist unique integers q and r such that a = bq + r, 0 ≤ r < b.
If b divides a, then r = 0 otherwise r satisfies 0 < r < b.
Question 4.
State the Fundamental theorem of Arithmetic.
Solution:
Every composite number can be ex¬pressed as a product of primes, and this factorization is unique except for the order in which the prime factors occur.
Question 5.
Given H.C.F. (96, 404) is 4 find LCM (96, 404).
Solution:
LCM × HCF = product of numbers
LCM × 4 = 96 × 404
LCM = 96×404/4
∴ LCM = 24 × 404 = 9696
Question 6.
If a and b are coprimes, then find the HCF (a,b).
Solution:
a, b are coprimes
Let 2, 3 are coprimes
HCF (2, 3) = 1
∴ HCF (a, b) = 1.
Question 7.
What is the LCM of 23 × 32 and 22 × 33?
22 × 33 = 2 × 2 × 2 × 3 × 3
22 × 33 = 2 × 2 × 3 × 3 × 3
LCM = 2 × 2 × 3 × 3 × 2 × 3
LCM = 23 × 33
Question 8.
What is the greatest possible speed at which a man can walk 52 km and 91 km in an exact number of hours ?
Solution:
52 = 2 × 2 × 13
91 = 13 × 7
HCF = 13
∴ Greatest possible speed = 13 km/hour
Question 9.
Assertion (A) : If HCF of 510 and 92 is 2, then the LCM of 510 and 92 is 32460.
Reason (R) : As HCF (a, b) × LCM (a, b) = a × b
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Solution:
D) Assertion (A) is false but reason (R) is true.
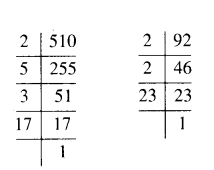
510 = 2 × 5 × 3 × 17; 92 = 2 × 2 × 23
HCF = 2
LCM = 2 × 2 × 3 × 5 × 17 × 23 ≠ 32460
Question 10.
If two positive integers a and b are written as a = x3y2 and b = xy3 where x, y are prime numbers, then find HCF (a, b).
Solution:
a = x3y2 = x . x . x . y . y
b = xy3 = x . y . y . y
HCF (a, b) = x . y . y = xy2
Question 11.
Find the LCM of smallest two digit composite number and smallest composite number.
Solution:
Smallest two digit composite number = 10
Smallest composite number = 4
10 = 2 × 5
4 = 2 × 2
∴ LCM = 2 × 5 × 2 = 20
Question 12.
Assertion (A) : The HCF of two numbers is 5 and their product is 150. Then their LCM is 40.
Reason (R) : For any two positive integers a and b, HCF (a, b) × LCM (a, b) = a × b.
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Solution:
D) LCM × HCF = product of numbers
40 × 5 = 200
Given product = 150
False.
Question 13.
The number (5 - 3√5 + √5) is ...... .
A) an integer
B) a rational number
C) an irrational number
D) a whole number
Solution:
C) an irrational number
5 - 3√5 + √5
= 5 - 2√5 , is an irrational number.
Question 14.
What is LCM of (23 × 3 × 5) and (24 × 5 × 7)?
Solution:
LCM of (23 × 3 × 5) and (24 × 5 × 7)
= 24 × 3 × 5 × 7
= 16 × 15 × 7
= 1680
Question 15.
If the HCF of 360 and 64 is 8 then their LCM is ...... .
A) 2480
B) 2780
C) 512
D) 2880
Solution:
D) 2880
LCM × HC = Product of numbers
LCM × 8 = 360 × 64
LCM = 360×64/8
= 45 × 64
= 2880
Question 16.
What is the ratio of HCF to LCM of the least composite number and the least prime number ?
Solution:
Least composite number = 4
Least prime number = 2
HCF of 2, 4 = 2
LCM of 2, 4 = 4
HCF : LCM = 2 : 4 = 1 : 2
Question 17.
Assertion (A) : The number 5n
cannot end with the digit ‘ 0’ where is in a natural number.
Reason (R) : Prime factorisation of 5 has only two factors 1 and 5.
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Solution:
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Question 18.
What is (HCF × LCM) for the number 30 and 70?
Solution:
30 = 2 × 3 × 5
70 = 2 × 5 × 7
LCM = 2 × 3 × 5 × 7 = 210
HCF = 2 × 5 = 10
∴ HCF × LCM = 10 × 210 = 2100
Question 19.
Statement A : √a is an irrational number where ‘a’ is a prime number
Statement B : The product of two irrational numbers is always irrational.
Identify the correct answer.
A) Statement A is true, statement B is true
B) Statement A is false, statement B is true
C) Statement A is true, statement B is false
D) Statement A is false, statement B is false
Solution:
A) Statement A is true, statement B is true
Question 20.
Three alarm clocks ring their alarms at regular intervals of 20 min, 25 min and 30 min respectively. If they first deep together at 12 noon, at what will they beep again for the first time?
Solution:

LCM = 2 × 5 × 2 × 5 × 3
= 300 min
= 300/60 hr = 5hr
∴ At 5 pm they beep again for the first time.
Question 21.
Write the decimal form of the rational number 7/22×5 .
Answer:
0.35
Question 22.
Which statement do you agree with ?
P : The product of two irrational numbers is always a rational number.
Q : The product of a rational and an irrational number is always an irrational number,
i) Only P
ii) Only Q
iii) Both P and Q
Answer:
ii) Only Q
Question 23.
Find the L.C.M. of 23 × 33 × 7, 2 × 33 × 5.
Solution:
L.C.M = 23 × 33 × 5 × 7
Question 24.
Express 725 in decimal form.
Solution:
7/25 = 7/5×5 - 7/52
Decimal form of ⇒ 7/25 = 0.28
Question 25.
Express 0.75 in p/q form.
Solution:
0.75 = 75/100 = 34
Question 26.
How many numbers in the following list are irrational ?
√11, 227, √36, π,
A) 3
B) 4
C) 5
D) 2
Answer:
A) 3
Question 27.
Find the LCM of 10, 15, 30.
Solution:
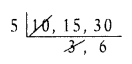
⇒ 6 × 5 = 30
Question 28.
State Fundamental Theorem of Arith¬metic.
Answer:
Statement of Fundamental Theorem of Arithmetic "Every composite number can be expressed as a product of primes, and this factorization is unique".
10th Class Maths Real Numbers 2 Marks Important Questions
Question 1.
Two positive integers a and b can be written as a = x3.y2 and b = x.y3. x and y are prime numbers. Find LCM of (a,b).
Solution:
Given positive integers are,
a = x
3.y
2 and b = x.y
3
a = x.x.x.y.y b = x.y.y.y
∴ LCM of (a, b) = x.x.x.y.y.y = x
3.y
3
Question 2.
If HCF (336, 54) = 6, find LCM (336,54).
Solution:
We know that,
HCF × LCM = Product of two numbers
6 × LCM = 336 × 54
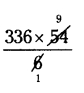
LCM
∴ LCM (336, 54) = 3024
Question 3.
Find the HCF of k, 2k, 3k, 4k and 5k, where k is a positive integer.
Solution:
k
2.k
3.k
2.2.k
5.k
∴ HCF is k.
Question 4.
Find the HCF of 1656 and 4025 by Euclid‘s division algorithm.
Solution:
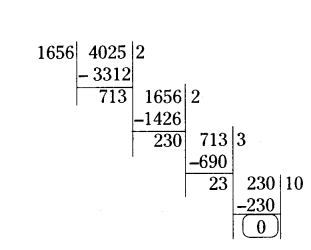
∴HCF of 1656 and 4025 is 23.
Question 5.
The HCF and LCM of two numbers are 9 and 360 respectively. If one number is 45, find the other number.
Solution:
HCF of two nurfibers = 9
LCM of two numbers = 360
One number a = 45
Other number b = ?
Product of two numbers = LCM × HCF
a × b = LCM × HCF
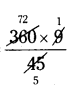
45 × b = 360 × 9 ⇒ b =
∴b = 72
Question 6.
Using Euclid’s algorithm, find HCF of 240 and 228.
Solution:
240 = 228 × 1 + 12
228= 12 × 19 + 0
∴ HCF of 240 and 228 is 12.
Question 7.
Find LCM of 576 and 512 by prime factorisation.
Solution:
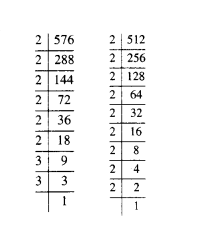
576 = 26 × 32;
512 = 29
LCM = 29 × 32 = 4608
Question 8.
Using prime factorization, find HCF and LCM of 96 and 120.
Solution:
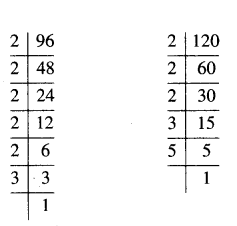
96 = 25 × 3
120 = 23 × 3 × 5
HCF = 23 × 3 = 8 × 3 = 24
LCM = 25 × 3 × 5 = 480.
Question 9.
Two numbers are in the ratio 2 : 3 and their LCM is 180. What is the HCF of these numbers?
Solution:
Let the two numbers are 2k and 3k.
LCM = 2 × 3 × k = 6k
∴ 6k = 180
k = 180/6
k = 30
2k = 2 × 30 = 60
3k = 3 × 30 = 90
60 = 2 × 2 × 3 × 5
90 = 2 × 3 × 3 × 5
HCF = 2 × 3 × 5 = 30
Question 10.
Find the HCF of the numbers 540 and 630 using prime factorisation method.
Solution:

Question 11.
Show that (15)n cannot end with the digit ‘O’ for any natural number ‘n’.
Solution:
(15)n = (3 × 5)n
= 3n × 5n
In the expansion of 3nand 5n, for any natural number ‘n’, there will not be any zero in the units place.
∴(15)n cannot end with the digit ‘O’ for any natural number ‘n’.
Question 12.
Find the LCM of 150 and 200.
Solution:
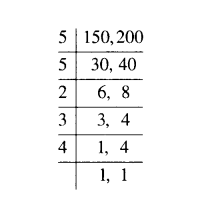
LCM = 5 × 5 × 2 × 3 × 4 = 600
Question 13.
Find the HCF and LCM of 72 and 120.
Solution:
72 = 2 × 2 × 2 × 3 × 3
120 = 2 × 2 × 2 × 3 × 5
LCM = 2 × 2 × 2 × 3 × 3 × 5 = 360
HCF = 2 × 2 × 2 × 3 = 24.
Question 14.
Express (15/4 + 5/40) as a decimal fraction without actual division.
Solution:
15/4 + 5/40 = 15/4 × 25/25 × 5/40 × 25/25
= 375/100 + 125/1000
= 3.75 + 0.125
= 3.875
Question 15.
If the prime factorization of a natural number (n) is 22 × 32 × 52 × 7.
How many consecutive zeroes will it have at the end of it ? Justify your answer.
Solution:
Given natural number (n) is 22 × 32 × 5 × 7 product of 23 × 32 × 52 × 7 is 12600, so the given number will have 2 consecutive zeroes at the end of it.
Question 16.
Find the HCF and LCM of 90, 144 by prime factorisation method.
Solution:
90 = 2 × 32 × 5
144 = 24 × 32
H.C.F = 2 × 32 = 18
L.C.M = 24 × 32 × 5 = 720
Question 17.
Is log3 81 rational or irrational ? Justify your answer.
Solution:
log3 81 = log334 = 4 log33 = 4
So log3 81 is a rational number.
Question 18.
Find the HCF of 24 and 33 by using division algorithm.
Solution:
33 = (24 × 1 ) + 9
24 = (9 × 2) + 6
9 = (6 × 1) + 3
6 = (3 × 2) + 0
H.C.F of 24 and 33 = 3.
Question 19.
Express 360 as a product of prime factors.
Solution:
360 = 2 × 2 × 2 × 3 × 3 × 5
= 23 × 32 × 51
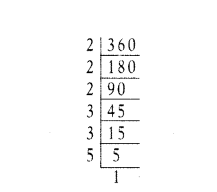
10th Class Maths Real Numbers 4 Marks Important Questions
Question 1.
If the HCF of 65 and 117 is express¬ible in the form 65m - 117, find the value of m.
Solution:
117 = 65 × 1 + 52
65 = 52 × 1 + 13
52 = 13 × 4 + 0
HCF is 13
So, 65m - 117 = 13
65m = 13 + 117
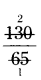
⇒ m =
∴ m = 2
Question 2.
The length, breadth and height of a room are 8 m 50 cm, 6 m 25 cm and 4 m 75 cm respectively. Find the length of the longest rod that can measure the dimensions of the room exactly.
Solution:
Given, length = 8 m 50 cm
= 850 cm
breadth = 6 m 25 cm
= 625 cm
height = 4 m 75 cm
= 475 cm
Length of the longest rod
= HCF of 850, 625, 475
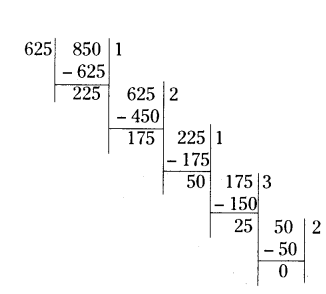
25 can divide 475.
∴ HCF of 850, 625, 475 is 25.
∴ The longest rod that can measure the dimensions of the room exactly is 25 cm.
Question 3.
Can two numbers have 15 as their HCF and 175 as their LCM ? Give reasons.
Solution:
15 cannot divide 175.
LCM of two numbers should not divide by HCF exactly.
∴ Two numbers cannot have their HCF as 15 and LCM as 175.
Question 4.
Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together ?
Solution:
The time to next together = LCM of (9, 12, 15)
9 = 3 × 3 = 32
12 = 2 × 2 × 3 = 22 × 31
15 = 3 × 5
LCM of (9, 12, 15) = 32 × 22 × 5
= 180 minutes.
∴Two bells will toll together after 180 minutes.
Question 5.
Given that √2 is irrational, prove that (5 + 3√2) is an irrational number.
Solution:
Given, √2 is irrational.
To prove 5 + 3√2 is irrational.
Let us assume 5 + 3√2 is rational.
So, it is in the form of a/b, a, b ∈ Z, b ≠ 0 and a, b are co-primes.
5 + 3√2 = a/b
⇒ 3√2 = a/b - 5
3√2 = a-5b/b
⇒ √2 = a-5b/3b
This shows the √2 is rational,
a - 5b and 3b are integers.
But we know that √2 is irrational.
This contradicts our assumption that 5 + 3√2 is rational.
Hence proved that 5 + 3√2 is irrational.
Question 6.
Express the number 0.3178 in the form of rational number a/b.
Solution:
Let x = 0.3178
x = 0.3178178178.
10000x = 10000 × 0.3178178178...
10000x = 3178.178178 .. → (1)
and 10x = 10 × 0.3178178178 ..
10x = 3.178178 .. → (2)
From (1) and (2)
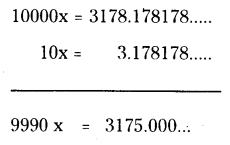
x = 31759990
⇒ x = 6351998
Question 7.
Given that √3 is an irrational number. Prove that (2 + √3) is an irrational number.
Solution:
Let 2 + √3 be a rational number.
2 + √3 = a/b, a, b ∈ Z and b ≠ 0
√3 = a/b - 2
√3 = a-2b/b
a-2b/b is rational = √3 is rational which is contradiction.
Thus 2 + √3 is irrational number.
Question 8.
Prove that 3 + 7√2 is an irrational number, given that √2 is an irrational number.
Solution:
Given √2 is an irrational.
Let if possible 3 + 7√2 is a rational number.
∴ 3 + 7√2 = a/b, b ≠ 0
7√2= a/b - 3
7√2 = a-3b/b
√2 = a-3b/7b
LHS is an irrational number.
RHS is a rational number as a and b are rational numbers.
LHS ≠ RHS
∴ Our assumption is wrong.
∴ 3 + 7√2 is an irrational number.
Question 9.
The traffic lights at three different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively. If they change simultaneously at 7 a.m. at what time will they change together next ?
Solution:
48 = 2 × 2 × 2 × 2 × 3 = 24 × 3
72 = 2 × 2 × 2 × 3 × 3 = 23 × 32
108 = 2 × 2 × 3 × 3 × 3 = 22 × 33
LCM = 24 × 33
= 432 seconds = 432/60 = 7.12 min
∴ They will change together next at 7 : 07 : 12 A.M.
Question 10.
Prove that (7 - 2√3) is an irrational number, given that √3 is an irrational number.
Solution:
Let 7 - 2√3 is a rational number.
7 - 2√3 = a/b, b ≠ 0 ⇒ 7 - a/b = 2√3
7b?a/b = 2√3 ? √3 = 7b?a/2b
LHS = √3 is an irrational number 7b - a
RHS = 7b?a/2b is a rational number as a 2b and b are rational numbers.
LHS ≠ RHS
∴ Our assumption is wrong,
∴ 7 - 2√3 is an irrational number.
Question 11.
Prove that 3 - 2√5 is an irrational number, given that J5 is an irrational number.
Solution:
Given √5 is an irrational number.
Let if possible 3 - 2√5 is a rational number.
3 - 2√5 = a/b, b ≠ 0 ⇒ 3 - a/b = 2√5
3b?a/b = 2√5 ⇒ √5 = 3b?a/2b
Given LHS is an irrational number.
RHS is a rational number as a and b are rational numbers.
∴ LHS ≠ RHS
∴ Our assumption is wrong.
∴ 3 - 2√5 is an irrational number.
Question 12.
Find the HCF and LCM of 26, 65 and 117 using prime factorisations.
Solution:
26 = 2 × 13
65 = 5 × 13
117 = 13 × 3 × 3
HCF = 13
LCM = 2 × 5 × 13 × 3 × 3 = 1170
Question 13.
Prove that √2 is an irrational number.
Solution:
Let if possible √2 is a rational number.
Let √2 = a/b, b ≠ 0 ⇒ (√2)2 = a2/b2
2 = a2/b2 ⇒ a2 = 2b2
a2 is a multiple of 2.
a2 is a multiple of 2.
Let a = 2c
(2c)2 = 2b2 ⇒ 4c2 = 2b2 ⇒ b2 = 2c2
b2 is a multiple of 2.
b is a multiple of 2.
∴ a and b have common factor 2.
which contradicts √2 is rational number.
∴ Our assumption is wrong.
∴ √2 is an irrational number
Question 14.
State Fundamental theorem of Arithmetic. Is it possible that HCF and LCM of two numbers be 24 and 540 respectively ? Justify your answer.
Solution:
Fundamental theorem of Arithmetic :
Every integer greater than one either is prime itself or is the product of prime numbers and that this factorization is unique. Apart from the order of the fac-tors.
Given HCF = 24, LCM = 540
Then LCM/HCF = 540/24
= 22.5 (not an integer).
Since, LCM is always multiple of HCF.
Hence, two rjumbers cannot have HCF and LCM as 24 and 540 respectively.
Question 15.
A fruit vendor has 990 apples and 945 oranges. He packs them into baskets. Each basket contains only one of the two fruits but in equal number. Find the number of fruits to be put in each basket in order to have minimum number of baskets.
Solution:
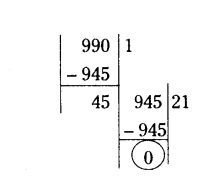
HCF of 990 and 945
990 = 1 × 945 + 45
945 = 45 × 21 + 0
Since. HCF of 900 and 945 is 45.
Thus, the fruit vendor should put 45 fruits in each basket to have minimum number of baskets.
Question 16.
An any contingent of 104 members is to march behind an army band of 96 members in a parade. The two groups are to march in the same number of columns. What is the maximum num¬ber of columns in which they can march ?
Solution:
Let x be the number of columns.
Then, x is the largest number which should divide both 104 and 96.
104 = 96 × 1 + 8
96 = 8 × 12 + 0
HCF of 104 and 96 is 8.
Hence 8 columns are required.
Question 17.
Prove that n2 - n is divisible by 2 for every positive integer n.
Solution:
Any positive integer is of the form 2q or 2q + 1, for some integer q.
If n = 2q
n2 - n = n(n - 1)
= 2q(2q - 1) [∵ q(2q - 1) = m]
= 2m
which is divisible by 2.
If n = 2q + 1
n(n - 1) = (2q + 1) (2q + 1 - 1)
= 2q(2q + 1)
= 2m [∵ q(2q + 1) = m]
which is divisible by 2.
So, n2 - n is divisible by 2 for every positive integer n.
Question 18.
Show that 7 - √5 is irrational, given that √5 is irrational.
Solution:
Let us assume to the contrary that 7 - √5 is rational.
7 - √5 = a/b, where a and b are co-primes and q ≠ 0.
√5 = 7 - a/b
√5 = 7b?a/b
7b-a/b is rational = √5 is rational.
which is contradictory.
∴ 7 - √5 is irrational.
Question 19.
Write any three numbers of two digits. Find the LCM and HCF for the above numbers by the Prime Factorization method.
Solution:
Take any three two digit numbers.
Say 8, 10 and 12.
Prime factorization of these numbers are
8 = 2 × 2 × 2
10 = 2 × 5
12 = 2 × 2 × 3
L.C.M. of 8, 10 and 12 is 2 × 22 × 5 × 3 = 120
H.C.F. of 8, 10 and 12 = 2.
Question 20.
Give an example tor each of the following :
i) The product of two irrational numbers is a rational number.
ii) The product of two irrational numbers is an irrational number.
Solution:
i) Let us consider two irrational numbers √2, √50.
Their product is
= (√2) (√50) = √100 = 10
which is a rational number,
ii) Again let us consider two irrational numbers = √3, √7
Their product = (√3) (√7) = 21??√
which is an irrational number.
Question 21.
i) Express the numbers 6825 and 3825
as a product of its prime factors.
ii) Find the H.C.F. and L.C.M. of the above numbers by using their products of prime factors.
iii) Justify your answer.
Solution:
i) Given numbers are 6825 and 3825 Prime factorisation of 6825 is 52 × 3 × 91
Prime factorisation of 3825 is 52 × 3 × 51
ii) HCF of 6825 and 3825 is = Product of the smallest power of each common prime factor of the number
= 3 × 52 = 25 × 3 = 75
LCM of 6825 and 3825 is = Product of the greatest power of each prime factors of the number.
= 52 × 3 × 91 × 51
iii) Product of two numbers
= 6825 × 3825 = 26105625
Product of LCM and HCF
= 75 × 52 × 3 × 91 × 51
= 26105625
∴ LCM × HCF = Product of two numbers.
Question 22.
Express 2016 as product of prime factors.
Solution:
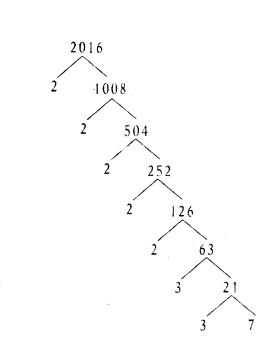
2016 = 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7
= 25 × 32 × 7
Question 23.
Write any two three digit numbers. Find their L.C.M. and G.C.D. by prime factorization method.
Solution:
Let the two three digit numbers be 100 and 200
100 = 22 × 52
200 = 23 × 52
L.C.M. = 23 × 52 = 200
G.C.D = 22 × 52 = 100
Question 24.
Lalitha says that HCF and LCM of the numbers 80 and 60 are 20 and 120 respectively. Do you agree with her ? Justify.
Solution:
We know that LCM × HCF = Product of the two numbers
Product of the two numbers = 80 × 60 = 4800
HCF × LCM = 20 × 120 = 2400
Since they a^e not equal, I don’t agree with her.
Question 25.
Find the HCF of 1260 and 1440 by using Euclid’s division lemma.
Solution:
Given numbers 1260 and 1440
1440 = 1260 × 1 + 180
1260 = 180 × 7 + 0
∴ HCF of 1260 and 1440 is 180.
Question 26.
Using the Euclid’s division lemma, find the HCF of 4830 and 759.
Solution:
Given numbers are 4830 and 759
4830 = 759 × 6 + 276
759 = 276 × 2 + 207
276 = 207 × 1 + 69
207 = 69 × 3 + 0
∴ HCF of 4830 and 759 = 69
Question 27.
Find the HCF and LCM of 12, 36 and 160 using the prime factorization method.
Solution:
12, 36 and 160
12 = 2 × 2 × 3 = 22 × 3
36 = 2 × 2 × 3 × 3 = 22 × 32
160 = 2 × 2 × 2 × 2 × 2 × 5 = 22 × 5
LCM = 25 × 32 × 5 = 1440
HCF = 2
10th Class Maths Real Numbers 8 Marks Important Questions
Question 1.
Find HCF of 81 and 237 and express it as a linear combination of 81 and 237 that is HCF (81, 237) = 81x + 237y for some x and y.
Solution:
Since 237 > 81
According to Euclid’s division algorithm
237 = 81 × 2 + 75
81 = 75 × 1 + 6
75 = 6 × 12 + 3
6 = 3 × 2 + 0
∴ HCF (81, 237) = 3
In order to write in the form of 81x + 237y
Now, 3 = 75 - 6 × 12
3 = 75 - (81 - 75 × 1) 12 [∵ 6 = 81 - 75 × 1]
= 75 - 81 × 12 + 75 × 12
= (75 + 75 × 12) - 81 × 12
= 75 × 13 - 81 × 12
= (237 - 81 × 2) × 13 - 81 × 12 [∵ 75 = 237 - 81 × 2]
= 237 × 13 - 81 × 2 × 13 - 81 × 12
= 237 × 13 - 81 × 26 - 81 × 12
= 237 × 13 - 81 × 38
= 81 × (-38) + 237 × (13)
= 81x + 237y
∴ x = -38 and y = 13
These values of x and y are not unique.
Question 2.
Show that √5 + √3 is an irrational number.
Solution:
To prove √5 + √3 is an irrational number.
Let √5 + √3 is a rational number.
Let √5 + √3 = a/b ,b ≠ 0
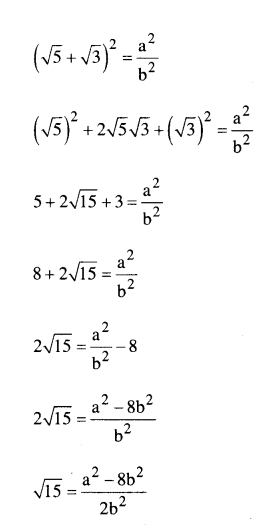
LHS 15√ is an irrational number.
RHS is a rational number as a, b are rational numbers.
∴ LHS ≠ RHS
∴ Our assumption is wrong.
∴ √5 + √3 is an irrational number.
Question 3.
Prove that √p + √q is an irrational number p, q are rational numbers.
Solution:
To prove √p + √q is an irrational number.
Let if possible √p + √q is a rational number.
Let √p + √q = ab ,b ≠ 0
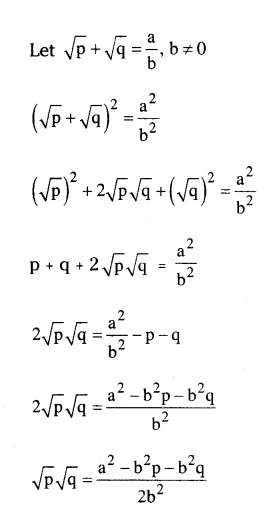
Question 4.
Let a, b, c and p be rational numbers such that p is not a perfect cube. If a + bp1/3 + cp2/3 = 0, then prove that a = b = c = 0.
Solution:
Given a + bp1/3 + cp2/3 = 0 .... (i)
Multiply both sides by p1/3, we get
ap1/3 + bp2/3 + cp = 0 .... (ii)
(i) × b ⇒ ab + b2 p1/3 + bcp2/3 = 0
(ii) × c ⇒ acp1/3 + bc p2/3 + c2p = 0
On subtraction
(ab + b2p1/3 + bcp2/3) - (acp1/3 + bcp2/3 + c2p) = 0
(b2 - ac) p1/3 + ab - c2p = 0
b2 - ac = 0 and ab - c2p = 0
b2 = ac and ab = c2p
b2 = ac and a2b2= c4 p2
a2(ac) = c4p2
a3c- p2c4 = 0
(a3 - p2c3) c = 0
a3 - p2c3 = 0 or c = 0
a3 - p2c3 = 0
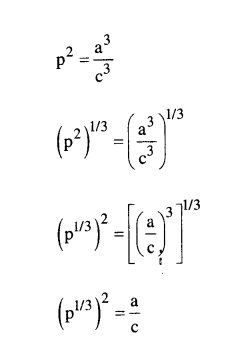
This is impossible as p1/3 is irrational a and a/c is rational, c
a3 - p2c3 ≠ 0
∴ c = 0
If c = 0, then b2 - ac = 0
b2 = 0
b = 0
Then a + bp1/3 + cp2/3 = 0
∴ a = 0
∴ a = b = c = 0.
Question 5.
Prove that √5 + √7 is irrational.
Solution:
To show that √5 + √7 is an irrational.
Let us prove this by contradiction.
So let us assume √5 + √7 = a
Where ‘a’ is a rational number.
⇒ √7 = a - √5 now squaring on both sides we get
(√7)2 = (a - √5)2
⇒ 7 = a2 + 5 - 2a√5
∴ 2a√5 = a2 + 5 - 7 = a2 - 2
⇒ √5 = a2-2/2a in which L.H.S part
√5 is an irrational and
RHS part(a2-2/2a) is a rational (∵ ‘a’is a rational)
So from the above a rational number and an irrational numbers are equal, which is impossible, which is wrong, So our assumption is wrong.
Hence given √5 + √7 won’t be a rational.
Therefore √5 + √7 is an irrational.
Question 6.
Show that 2 + 5√3 is irrational.
Solution:
Given that 2 + 5√3 is an irrational.
On the contrary. let us assume that 2 + 5√3 is a rational number
∴ 2 + 5√3 = p/q (q ≠ 0)
⇒ 5√3 = p/q - 2 = p-2q/q
⇒ √3 = (p-2q/5q)
Here p. q being integers we can say that p-2q/5q is a rational number. This contradicts the fact that √3 is an irrational number. This is due to our assumption "2 + 5√3 is a rational number’.
Hence our assumption is wrong.
∴ 2 + 5√3 is an irrational number.
Question 7.
Prove that √5 + √11 is irrational.
Solution:
Let us assume that √5 + √11 is rational number.
Let us √5 + √11 = ab where a, b are co - primes b ≠ 0
∴ √5 = a/b - √11
Squaring on both sides, we get
5 = a2/b2 + 11 - 2 a/b√11
Rearranging
2 a/b√11 = a2/b2 + 11 - 5 = a2/b2 + 6
√11 = a2+6b2/b2 × b/2a = a2+6b2/2ab
Since, a, b are integers a2+6b2/2ab is rational number.
So √11 is rational number.
This contradicts the fact that √11 is irrational number.
Hence √5 + √11 is irrational number.


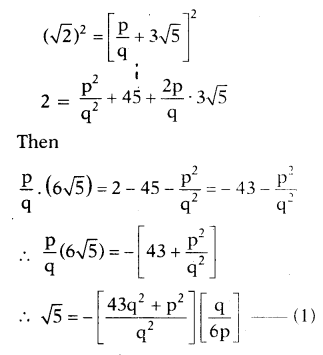
Since p and q are integers the RHS part of above equation (1) becomes a rational and LHS part √5 is an irrational one which is unfair.
So our assumption is wrong.
Then √2 - 3√5 is an irrational number.

An irrational number never be equal to a rational number.
So our supposition that √3 - √5 is not an irrationa! number is false.
∴ √3 - √5 is an irrational number.

(p2 - 8q2, 2q2 ∈ Z, 2q2 ≠ 0
but an irrational number can’t be equal to a rational number, so our supposition that √3 + √5 is not an irrational number is false.
∴ √ 3 + √5 is an irrational number.
Question 13.
Prove that √2 + √11 is an irrational number.
Solution:

but 15 is an irrational number.
An irrational number never be equal to a rational number.
So our supposition that √ 5 - √ 3 is not an irrational number is false.
∴ √ 5 - √ 3 is an irrational number.

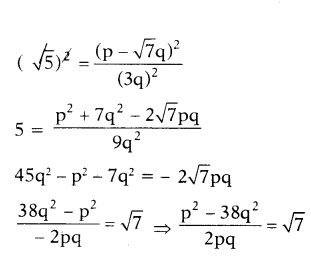
p2-38q2/2pq is a rational number but
√7 is an irrational number. This is a contradiction to the fact that √7 is an irrational number. So our assumption is wrong.
AP State Syllabus 10th Class Maths 1st Lesson Important Questions and Answers Real Numbers
Question 1.
Find the HCF of 60 and 100 by using Euclid division lemma.
Solution:
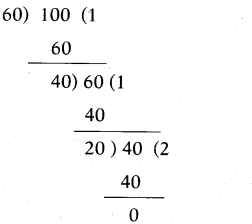
∴ HCF of 60 and 100 is 20

Question 5.
If x2 + y2 = 7xy, then prove that log(x+y/3)=1/2(logx+logy)
Sol.
Given x2 + y2 = 7xy now add (2xy) on both sides. We get
x2 + y2 + 2xy = 7xy + 2xy = 9xy
Considering square root on both sides we get
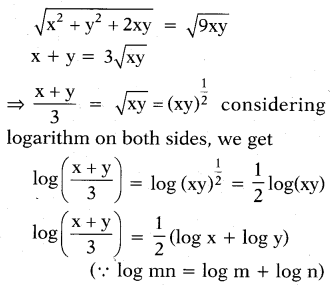
Question 6.
Find the HCF of 1260 and 1440 by us¬ing Euclid‘s division lemma.
Solution:
Given numbers 1260 and 1440
1440 - 1260 x 1 + 180
1260 = 180 x 7 + 0
∴ HCF of 1260 and 1440 is 180.
Question 7.
Using the Euclid’s division lemma, find the HCF of 4830 and 759.
Solution:
Given numbers are 4830 and 759
4830 = 759 x 6 + 276
759 = 276 x 2 + 207
276 = 207 x 1 + 69
207 = 69 x 3 + 0
∴ HCF of 4830 and 759 = 69
Question 10.
Express 1.2333333 In p/q form where p and q are co-primes.
Solution:
Let x = 1.2333333
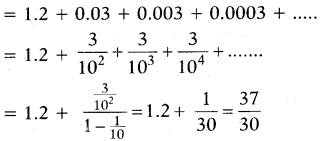

3 divides b2 ⇒ 3 divides b (2)
From (1) & (2)
3 is a common factor for a and b This contradicts the fact that a and b are coprimes
∴ Our assumption that ∴3 is rational is wrong.
∴ √ 3 is irrational.
Question 13.
Show that 2+5√3 is irrational.
Solution:
Given that 2+5√3 is an irrational. On the contrary, let us assume that 2+5√3 is a rational number.
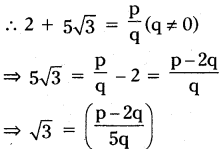
Here p, q being integers we can say that p?2q/5q is a rational number. This contradicts the fact that √3 is an irra-tional number. This is due to our as-sumption "2 + 5∴3 is a rational num-ber".
Hence our assumption is wrong.
∴ 2 + 5√3 is an irrational number.
Question 14.
Prove that √5+√11 is irrational.
Solution:

but 15 is an irrational number.
An irrational number never be equal to a rational number.
So our supposition that √5+√3 is not an irrational number is false.
∴ √5+√3 is an irrational number.

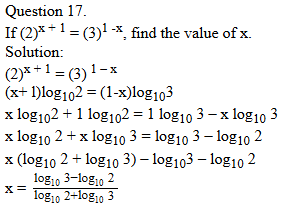
Fundamental Theorem of Arithmetic :
Question 18.
Support the Fundamental theorem of Arithmetic by considering some examples.
Solution:
Every composite number can be ex-pressed as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.
Ex: 1) Now let us consider a com¬posite number 186.
∴ 186 can be factorised 2 x 3 x 31 where 2, 3 and 31 are primes.
Ex: 2) Now consider another com¬posite number 384.
∴ 384 = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 3 = 27 x 3 where these 2 and 3 are primes.
Thus we can express any composite number as a product of some primes. Thus the theorem is valid.
Question 19.
Write 210 as product of prime factors.
Solution:
210 = 3 x 70
= 3 x 7 x 10
= 3 x 7 x 5 x 2
∴ way of 2 x 3 x 5 x 7.
So the composite number 210 can be written as product of primes 2, 3, 5 and 7 in the way of 2 x 3 x 5 x 7.
Question 20.
Is the units digit in the value of 6n where ‘n’ is a natural number is zero? Justify your answer.
Solution:
No, the units number in the value of 6n where ‘n’ is a natural number will not be zero.
Why because, if a (composite) number is written as product of prime factors having 2 and 5 then the units digit becomes zero.
In this case
6 = 2 x 3 that means 6 has only 2 in its factors but not 5.
Hence in the value of 6n, the units digit will not be equal to zero.
Question 21.
If the HCF of 306 and 657 is 9, then find their LCM.
Solution:
The given two numbers are 306, and 657.
HCF of given numbers = 9
From the formula
LCM x HCF = Product of given two numbers
(LCM) (9) = 657 x 306
∴ LCM = 657×306/9 = 22, 338
∴ LCM of 306 and 657 is 22,338.
Question 22.
Find the HCF of 45,75 from Euclid’s division lemma.
Solution:
Let us write 45 and 75 in the form of a = bq + r where a = 75, b = 45
∴ 75 = 45 (1) + 30
Again using lemma a = bq + r, where
a = 45, and b = 30,
we get, 45 = 30 (1) + 15
then 30 = 15 (2) + 0
Here we get remainder ‘0’ when we
divide it by 15.
So 15 is HCF of 45 and 75.
Question 23.
How do you say 7 x 11 x 13 + 13 and 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 are complex numbers ? Explain it.
Solution:
The given
7 x 11 x 13 + 13= 13 [(7 x 11) + 1] = 13 [77 + 1] =13 x 78
So we can express 7 x 11 x 13 + 13 as product of 13 and 78 that means 13 and 78 are factors of given 7 x 11 x 13 + 13. Hence it is a composite number.
Similarly
7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 = 5[(7 x 6 x 4 x 3 x 2 x 1) + 1]
= 5 [1008 + 1] = 5 x 1009
That means 7 x 6 x 5 x 4 x 3 x 2 x 1 + 5 can be written as product of two factors 5 and 1009. Hence (7 x 6 x 5 x 4 x 3 x 2 x 1) + 5 is a complex number because it has more than 2 factors.
Logarithms :
Question 24.
Express the following in log form,

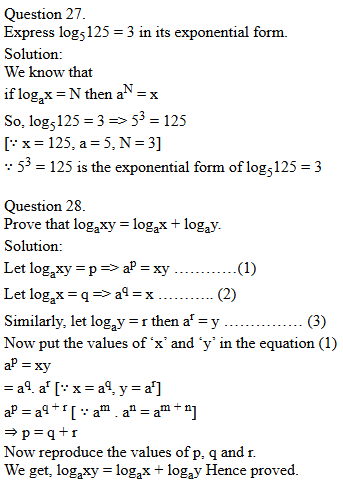

Question 32.
Write the differences between rational and irrational numbers.
Solution:

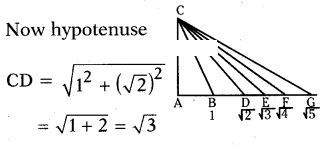
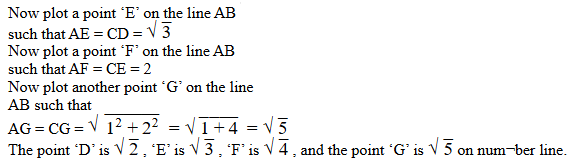
Question 34.
Find the value of √2 upto 4 decimals.
Solution:

Question 35.
Where do we use irrational numbers in our day to day life ?
Solution:
1. We use the value of ? in finding perimeter and area of a circle (n is an irrational).
2. To find the length of the diagonal of a square we use √2 which is an irrational one.
3. To find the T.S.A., curved surface area and volumes of solids viz cyl-inder, sphere, and cone etc. We use K in above case which is an irratio¬nal one.
4. For calculation of compound inter-est, E.M.I. (equal monthly install-ments) in Banks they use ‘e’ value which is an irrational one.
5. We use these numbers in space and economics related matters thor-oughly.
Question 36.
Establish the relation between diago-nal and side of a square.
Solution:
Let the side of square ABCD = a
Then its diagonal AC = Hypotenuse of ∆ABC.
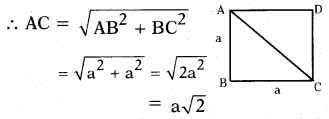
So the diagonal of a square is a √2 when its side is ‘a’.
Question 37.
Is π a rational or irrational ? Give reasons.
Solution:
π is an irrational number. The value of
π is approximately 22/7
But not exactly,
22/7 = 3.14285714286. eventhough 22
22/7 is in the form of p/q.
π is an irrational.