Motion

Improve Your Learning

Question 1.
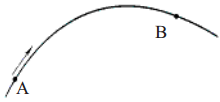
As shown in following figure, a point traverses the curved path.
Draw the displacement vector from given points A to B.

Answer

As the point traverses from A to B, the displacement is the shortest distance between A and B. Hence the displacement vector will be as follows.

Question 2.
“She moves at a constant speed in a constant direction.” Rephrase the same sentence in fewer words using concepts related to motion. (AS 1)

Answer:
“She moves with constant velocity”.

Reason :
Constant speed in a constant direction is nothing but ‘constant velocity’.

Question 3.
What is the average speed of a Cheetah that sprints 100 m in 4 sec? What if it sprints 50 m in 2 sec? (AS 1, AS7)

Answer:

Question 4.
Correct your friend who says, “The car rounded the curve at a constant velocity of 70 km/h”. (AS 1)

Answer:
“The car rounded the curve at a constant speed of 70 km/h”.

Reason :
In a circular motion, speed remains constant but velocity changes.

Question 5.
Suppose that the three balls shown in figure below start simultaneously from the top of the hills. Which one reaches the bottom first? Explain.

Answer:
Ball from first hill reaches the bottom first.
Reason :

1. In the first hill, the ball has uniform rectilinear motion.
2. So, the speed and velocity have same magnitude and direction.
3. In the second and third hills, the ball takes curved path.
4. So, the direction of velocity changes.

Question 6.
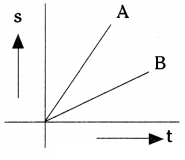
In the figure given below distance vs time graphs showing motion of two cars A and B are given. Which car moves fast? (AS 1)

Answer:
Car A moves fast.

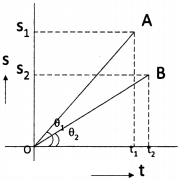
Reason :

1. If we draw perpendiculars to X and Y axes from A and B respectively, we can observe that A covers large distance (S₁) within a short time (t₁).
2. Find the slopes of the lines OA and OB at any instant. Slope of OA is high. Hence car A moves faster.

Question 7.
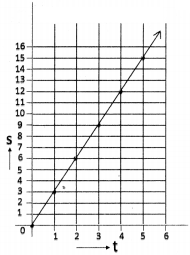
Draw the distance vs time graph when the speed of a body increases uniformly. (AS 5)

Answer:
Let us consider a car moves as shown in the table.

Time (t) sec	Distance in meters
0 sec	0 meters
1 sec	3 meters
2 sec	6 meters
3 sec	9 meters
4 sec	12 meters
5 sec	15 meters

Now draw a s-t graph.

Question 8.
Draw the distance-time graph when its speed decreases uniformly. (AS 5)

Answer:
Let us consider the movement of a car after applying brakes.

Time (t) sec	Distance in meters
0 sec	20 meters
1 sec	18 meters
2 sec	16 meters
3 sec	14 meters
4 sec	12 meters
5 sec	10 meters

Now draw distance-time graph.

Question 9.
A car travels at a speed of 80 km/h during the first half of its running time and at 40 km/h during the other half. Find the average speed of the car. (AS 1, AS 7)

Answer:
Let the total running time = x hrs

Question 10.
A car covers half the distance at a speed of 50 km/h and the other half at 40 km/h. Find the average speed of the car. (AS 1, AS 7)

Answer:
Let the total distance = x km.
First half is covered with a speed of 50 km/h.

Question 11.
Derive the equation for uniform accelerated motion for the displacement covered in its n^thsecond of its motion. (s_n= u + a ( n - 1/2) (AS 1)

Answer:
We know that distance travelled by an object in t seconds Is s = ut + 1/2 at²
∴ Distance travelled in ‘n’ seconds, s_{(n sec)}= un + 1/2 an² ………. (1)
Distance travelled in (n - 1) seconds, s_{(n - 1)}= u(n -1) + 1/2 a(n - 1)² …….. (2)

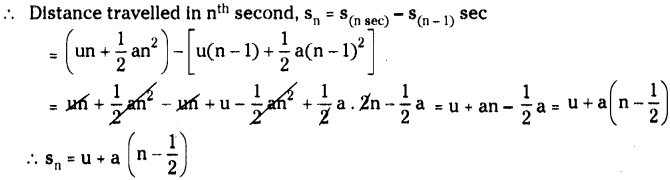
Question 12.
A particle covers 10m in first 5 sec and 10m in next 3 sec. Assuming constant acceleration. Find initial speed, acceleration and distance covered in next 2 sec. (AS 1, AS 7)

Answer:
Distance covered in first 5 sec = 10

To find the distance covered in next 2 sec, we have to find the initial speed after 8 sec
i.e., the final velocity after 8 sec.

Question 13.
A car starts from rest and travels with uniform acceleration ‘α’, for some time and then with uniform retardation ‘β’ and comes to rest. The time of motion is “t”. Find the maximum velocity attained by it. (αβt/(α+β)) (AS 1, AS 7)

Answer:
Acceleration a = a m/sec²
Initial speed u = 0 m/sec
Let the time be t₁sec.
From equation v = u + at
⇒ v = 0 + αt₁

Retardation a = - β m/sec²
Initial speed ‘u’ is equal to the final
velocity with acceleration ‘α’
= u = αt₁m/sec
Final velocity v = 0 m/sec
Let the time be t₂sec

Question 14.
A man is 48m behind a bus which is at rest. The bus starts accelerating at the rate of 1 m/s², at the same time the man starts running with uniform velocity of 10 m/s. What is the minimum time in which the man catches the bus? (AS 1, AS 7)

Answer:
Bus is at rest.
∴ u = 0; a = 1 m/sec²
Let the bus cover the distance ‘s’ in ‘n’ seconds.

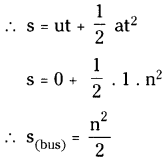
A man running with uniform velocity, v = 10 m/sec.
Distance covered by man in n seconds = 10 nm.
But after ‘n’ seconds the man catches the bus.

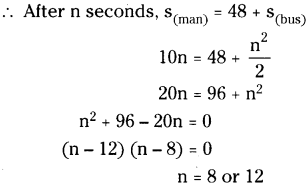
∴ The minimum time in which the man catches the bus is 8 sec.

Question 15.
A body leaving a certain point “O” moves with a constant acceleration. At the end of the fifth second, its velocity is 1.5 m/s. At the end of the sixth second, the body stops and then begins to move backwards. Find the distance traversed by the body before it stops. Determine the velocity with which the body returns to point “0”. (AS 1)

Answer:
Velocity in 5^thsec = 1.5 m/sec ; The body comes to rest in 6^thsec.
∴ Final velocity in 6^thsec, v = 0
∴ Acceleration in 6^thsec is v = u + at ⇒ 0 = 1.5 + a. 1 ⇒ a = -1.5 m/sec²
[The velocity in 5^thsec becomes the initial velocity for 6^thsec]

After 6 sec, the body comes to rest.
∴ v = 0, a = -1.5 m/sec², u = ?, t = 6 sec.
v = u + at ⇒ 0 = u - 1.5 × 6 ⇒ u = 9 m/sec.
∴ Distance traversed by the body in 6 sec. i.e., before it stops.
s = ut +1/2at² = 9 × 6 +1/2× - 1.5 × 6² = 54 - 27 = 27m.
For backward journey,
u = 0 m/sec, t = 6 sec, a = -1.5 m/sec²
v = u + at ⇒ v = 0 - 1.5 × 6 ⇒ v = - 9
∴ Velocity for backward journey is - 9 m/sec.

Question 16.
Distinguish between speed and velocity.(AS 1)

Answer:

Speed	Velocity
1. The distance covered in unit time is called average speed.	1. The displacement of an object per unit time is called average velocity.
2. Speed =Distance/Time	2. Velocity =Displacement/Time
3. Speed is scalar.	3. Velocity is vector.
4. Speed gives the idea of how fast the body moves.	4. Velocity gives the idea of how fast the body moves in specified direction.

Question 17.
What do you mean by constant acceleration? ((AS 1)

Answer:

• Acceleration is the rate of change of velocity.
  2
• It gives an idea how quickly velocity of a body is changing.
• Acceleration is uniform, when in equal intervals of time, equal changes of velocity occurs.
• For example, while driving a car, if we steadily increase the velocity from 30 km/h to 35 km/h in 1 sec and 35 km/h to 40 km/h in the next second and so on. In this case the acceleration is 5km/h, is said to be constant acceleration.

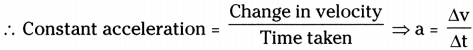
Question 18.
When the velocity is constant, can the average velocity over any time interval differ from instantaneous velocity at any instant ? If so, give an example; if not, explain why. (AS 2, AS 1)

Answer:
No. Here velocity is constant.
∴ Average velocity over any time interval is same and the instantaneous velocity at any instant is same.

Ex : Let us consider a car moves on a straight road with constant velocity say 10 m/s.
1) Now let the distance covered (AB) by the car in 1 s = 10 m.

2) Distance covered in 2s (AC) = 20 m.
Average velocity from A to C is 20m/2s= 10 m/s.

3) Instantaneous velocity at A or B or C at any point = 10 m/s.

Question 19.
Can the direction of velocity of an object reverse when its acceleration is constant? If so give an example; if not, explain why? (AS 2, AS 1)

Answer:
Yes. In case of a vertically projected body, while the body is moving up, the direction of velocity is upward, whereas while it is falling down, the direction of velocity is downward. Acceleration in both the cases is constant (numerically).

Question 20.
A point mass starts moving in a straight line with constant acceleration V’. At a time t after the beginning of motion, the acceleration changes sign, without change in magnitude. Determine the time t0 from the beginning of the motion in which the point mass returns to the initial position. (AS 1)

Answer:

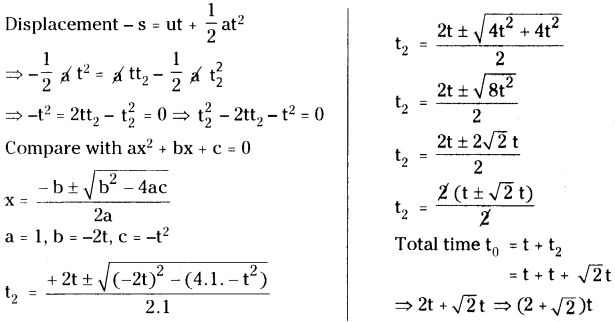
Question 21.
Consider a train which can accelerate with an acceleration of 20 cm/s² and slow down with deceleration of 100 cm/s². Find the minimum time for the train to travel between the stations 2.7 km apart. (AS 1)

Answer:
Let the Acceleration of the train a = 20 cm/s²
Deceleration of the train β = 100 cm/s²
Distance between the two stations s = 2.7 km = 27 × 10⁴cm
Let the minimum time for the train to travel between the two stations is t sec.

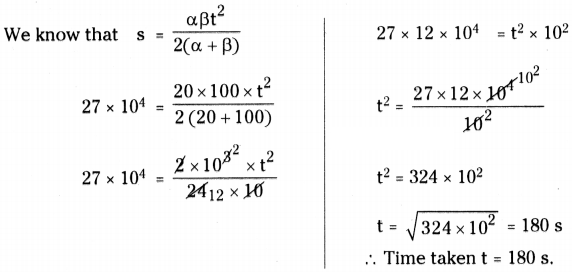
Question 22.
You may have heard the story of the race between the rabbit and tortoise. They started from same point simultaneously with constant speeds. During the journey, rabbit took rest somewhere along the way for a while. But the tortoise moved steadily with lesser speed and reached the finishing point before rabbit. Rabbit woke up and ran, but rabbit realized that the tortoise had won the race. Draw distance vs time graph for this story. (AS 5)

Answer:

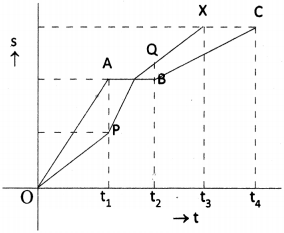
1. OX - movement of tortoise.
2. OABC - movement of rabbit
3. Rabbit and tortoise start at O’.
4. After time tj rabbit is at A and tortoise is at P.
5. Rabbit takes rest up to time t₂.
6. After time t₂, tortoise is at Q, but rabbit has no displacement.
7. After time t₃, the tortoise reaches the destination ‘X’.
8. But rabbit reaches the destination after time t₄.

Question 23.
A train of length 50 m is moving with a constant speed of 10 m/s. Calculate the time taken by the train to cross an electric pole and a bridge of length 250 m. (AS 1)

Answer:
Length of the train 50 m.; Speed of the train v = 10 m/s.
Distance travelled while crossing an electric pole = Length of the train = s = 50 m.
∴ Time taken to cross the electric pole ‘t’ =s/v⇒t=50/10= 5 s.
Length of the bridge = 250 m.
Distance travelled while crossing the bridge = Length of train + Length of bridge
= 50 + 250 = 300 m.
∴ Time taken to cross the bridge =300 m/10 m/s = 30 sec.

Question 24.
Two trains each of having a speed of 30 km/h are headed at each other in opposite direction on the same track. A bird flies off one train to another with a constant speed of 60 km/h when they are 60 km apart till before they crash. Find the distance covered by the bird and how many trips the bird can make from one train to the other before they crash. (AS 1)

Answer:
Speed of each train = 30 km/hr
Speed of the bird = 60 km/hr
Distance between the two trains = 60 km
These two trains crash in one hour.
The bird flies a distance of 60 km till before the two trains crash.
The bird can make number of trips (infinity) before they crash.

Question 25.
A Stone dropped from top of a well reaches the surface of water in 2 seconds, find the velocity of stone while it touches the surface of water and what is the depth of the water surface from top of well (g=10m/s²) (Using V = U + at, S = Ut + 1/2 at²)

Answer:
Given that
t = 2s
u = 0 m/s [∵ free fall body]
v = ?
Depth s = ?
a = g = 10 m/s²

i) v = u + at
v = 0 + 10 × 2 = 20 m/s

ii) s = ut + -1/2at²
= 0 +1/2× 10 × 2²
=1/2× 10 × 4
= 20 m
Hence, velocity of stone while it touches the surface of water = 20 m/s
Depth of the water surface from the top of well = 20 m.

Question 26.
An object moving with 6m per second execute an acceleration 2 m/s² in next 3 seconds. How much distance it covered? (s = ut + 1/2 at²)

Answer:
u = 6 m/s; t = 3 sec; a = 2 m/s²
s = ut +1/2 at²
= 6 × 3 +1/2 × 2 × 3² = 18 + 9 = 27 m
The object covers 27 m in 3 sec.

Question 27.
A car stopped after travelling distance 8 m due to applying brakes at the speed of 40 m/s. Find acceleration and retardation of car in that period, (v² - u² = 2as)

Answer:
Here u = 40 m/s; v = 0 (vehical stopped); s = 8 m; a =?
v² - u² = 2as 0 - 40² = 2 × a × 8
a =-(40)(40)/2×8=-100m/s
Acceleration = 100 m/s² with retordation on (-sign).