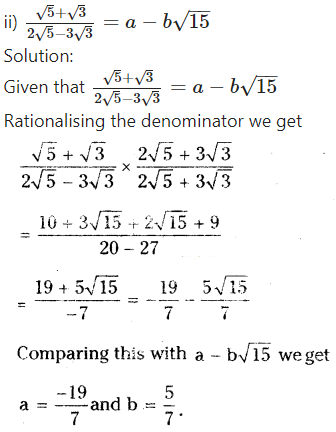Question 1.
a) Write any three rational numbers.
Solution:
3/4,5/9,2/7
b) Explain rational number is in your own words.
Solution:
A number which can be expressed in algebraic form i.e., in p/q form is called a rational number.
E.g.: 3/5, ?4/9 etc.
Question 2.
Give one example each to the following statements.
i) A number which is rational but not an integer.
:
7/11
ii) A whole number which is not a natural number.
Solution:
‘0’ (Zero)
iii) An integer which is not a whole number.
Solution:
-8
iv) A number which is natural number, whole number, integer and rational number.
Solution:
5
v) A number which is an integer but not a natural number.
Solution:
-4
Question 3.
Find five rational numbers between 1 and 2.
Solution:
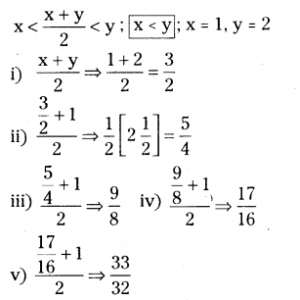
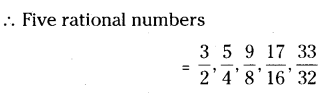
Question 4.
Five rational numbers between 2/3 and 3/5
Solution:

Question 5.
Represent 8/5 and -8/5 on a number line.
Solution:
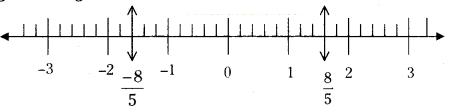
Step 1 : Draw a number line.
Step 2 : Divide each unit into 5 equal parts.
Step 3 : Take 8 -equal parts from ‘0’ on its right side and mark it as 8/5 (similarly) on left side -8/5.
Question 6.
Express the following rational numbers as decimal numbers.
Solution:
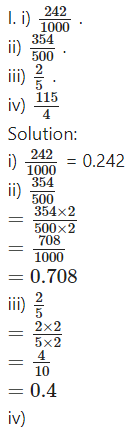
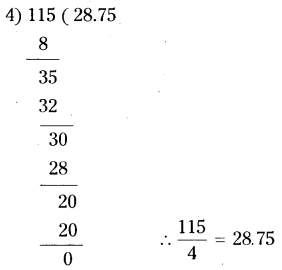
II. i) 2/3
Solution:

ii) ?25/36
Solution:

iii) 22/7
Solution:

iv) 11/9
Solution:

Question 7.
Express each of the following decimals in p/q form where q ≠ 0 and p, q are integers.
i) 0.36
Solution:
0.36 =36/100=925
ii) 15.4
Solution:
15.4 =154/10=77/5
iii) 10.25
Solution:
10.25 =1025/100=41/4
iv) 3.25
Solution:
3.25 =325/100=13/4
Question 8.
Express each of the following decimal number in the p/q form.

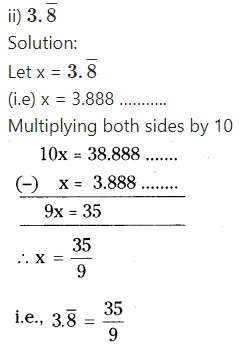

x = 0.12777
Multiplying by 10 on both sides
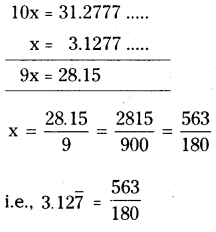
Question 9.
Without actually dividing find which of the following are terminating
decimals.
i) 325
Solution:
Check the denominator, if it consists of 2’s or 5’s or combination of both then only it reduces to a terminating decimal.
25 = 5 x 5
Hence 3/25 is a terminating decimal.
ii) 11/18
Solution:
Denominator 18 = 2 × 3 × 3,
hence 11/18 is a non-terminating decimal 13
iii)13/20
Denominator 20 = 2 × 2 × 5,
hence 13/20 is a terminating decimal.
iv)41/42
Solution:
Denominator 42 = 2 × 3 × 7,
hence 41/42 is a non-terminating decimal.
Question 1.
Classify the following numbers as rational or irrational.
- i)√27
- ii)√441
- iii) 30.232342345
- iv) 7.484848
- v) 11.2132435465
- vi) 0.3030030003
Solution:
- i)√27 irrational number
- ii)√441 = 21 - rational
- iii) 30.232342345 - irrational number
- iv) 7.484848 - rational number
- v) 11.2132435465 - irrational number
- vi) 0.3030030003 - irrational number
Question 2.
Explain with an example how irrational numbers differ from rational numbers ?
Solution:
Irrational numbers can’t be expressed in p/q form where p and q are integers and q ≠ 0.
E.g.√2,√3;√5,√7 etc.
Where as a rational can be expressed in pq form
E.g. :- -3 = ?3/1 and 5/4 etc.

Question 4.
Find two irrational numbers between 0.7 and 0.77.
Solution:
Two irrational numbers between 0.7 and 0.77 can take the form
0.70101100111000111…………. and 0.70200200022……………
Question 5.
Find the value of √5 uPto 3 decimal places.
Solution:

[√5 is not exactly equal to 2.2350679………….. as shown ¡n calculators]
Question 6.
Find the value of √7 upto six decimal places by long division method.
Solution:

Question 7.
Locate √10 on number line.

Step 1 : Draw a number line.
Step 2 : Draw a rectangle OABC at zero with measures 3 x 1. i.e., length 3 units and breadth 1 unit.
Step 3 : Draw the diagonal OB.
Step 4 : Draw an arc with centre ‘O’ and radius OB which cuts the number line at D.
Step 5 : ‘D’ represents (sqrt{mathrm{10}}[latex] on the number line.
Question 8.
Find atleast two irrational numbers between 2 and 3.
Solution:
An irrational number between a and b is Tab [latex]sqrt{mathrm{ab}}) unless ab is a perfect square.
∴ Irrational number between 2 and 3 is √6
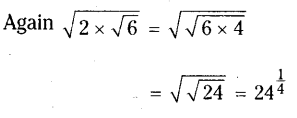
∴ Required irrational numbers are 61/2, 241/4
Method – II:
Irrational numbers between 2 and 3 are of the form 2.12111231234………….. and 3.13113111311113…….
Question 9.
State whether the following statements are true or false. Justify your answers.
Solution:
- Every irrational number is a real number – True (since real numbers consist of rational numbers and irrational numbers)
- Every rational number is a real number – True (same as above)
- Every rational number need not be a rational number – False (since all rational numbers are real numbers).
- √n is not irrational if n is a perfect square – True. (since by definition of an irrational number).
- √n is irrational if n is not a perfect square – True. (same as above)
- All real numbers are irrational – False (since real numbers consist of rational
Question 1.
Visualise 2.874 on the number line, using successive magnification.
Solution:
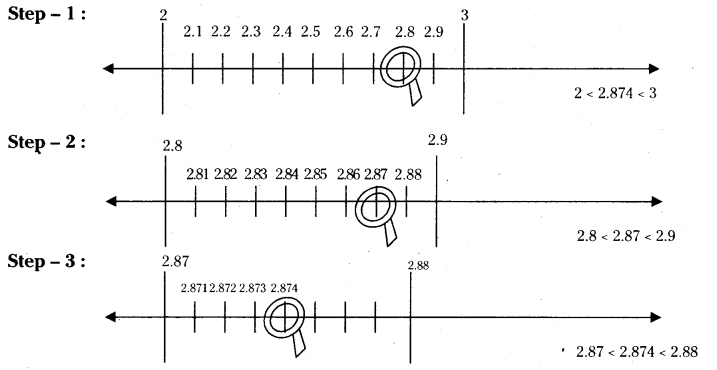
Question 2.
Visualise5.28 on the number line, upto 3 decimal places.
Solution:
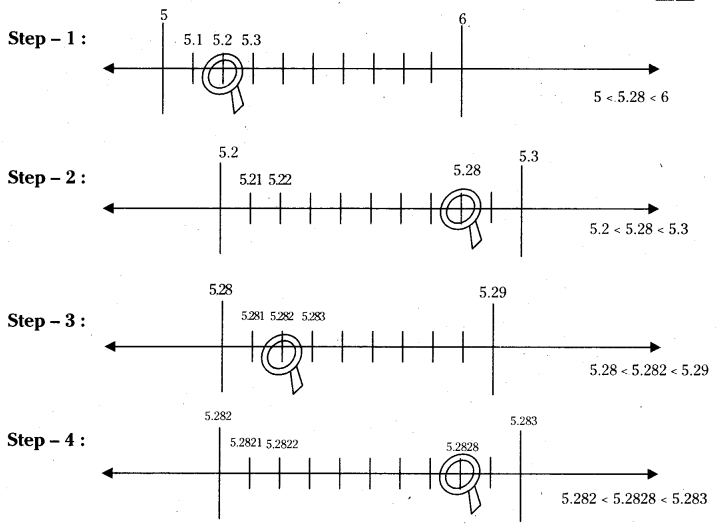
Question 1.
Simple the following expressions.
i) (5 + √7) (2 + √5)
Solution:
(5 + √7) (2 + √5)
= 10 + 5√5 + 2√7 + √35
ii) (5 + √5) (5 - √5)
Solution:
(5 + √5) (5 - √5)
= 52 + (√5)2
= 25 - 5 = 20
(iii) (√3 + √7)2
Solution:
(√3 + √7)2
= (√3)2 + (√7)2 + 2(√3)(√7)
= 3 + 7 + 2√21
= 10 + 2√21
iv) (√11 - √7) (√11 + √7)
= (√11)2 - (√7)2<.sup>
= 11 - 7 = 4
Question 2.
Classify the following numbers as rational or irrational.
i) 5 - √3
ii) √3 + √2
iii) (√2 - 2)2
iv) 2√7/7√7
v) 2π
vi) 1/√3
vii) (2 +√2) (2 - √2)
Solution
i) 5 - √3 - irrational
ii) √3 + √2 - irrational
iii) (√2 - 2)2 - irrational
iv) 2√7/7√7 - irrational
v) 2π - Transcendental number. (not irrational)
vi) 1/√3 - irrational
vii) (2 +√2) (2 - √2) - rational
Question 3.
In the following equations, find whether variables x, y, z etc., represents rational or irrational numbers.
- i) x2= 7
- ii) y2= 16
- iii) z2= 0.02
- iv) u2=17/4
- v) w2= 27
- vi) t4= 256
Solution:
i) x2 = 7
⇒ x = √7 is an irrational number.
ii) y2 = 16 ⇒ y = 4 is a rational number.
iii) z2 = 0.02 ⇒ z = √0.02 is an irrational number.
iv) u2 = 174 ⇒ x = √17/2 is an irrational number.
v) w2 = 27 ⇒ w = 3√3 an irrational number.
vi) t4 = 256 ⇒ t2 = √256 = 16
⇒ t = √16 = 4 is a rational number
Question 4.
The ratio of circumference to the diameter of a circle c/d is represented by π. But we say that π is an irrational number. Why?
Question 5.
Rationalise the denominators of the following.
i) 1/3+√2
Solution:
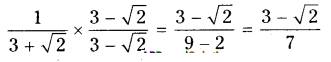
ii) 1/√7?√6
Solution:
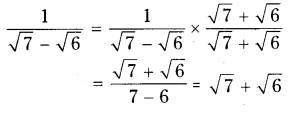
iii) 1/√7
Solution:
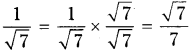
iv) √6/√3?√2
Solution:
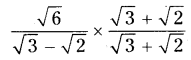
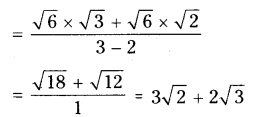
Question 6.
Simplify each of the following by rationalising the denominator.
i) 6?4√2/6+4√2
Solution:
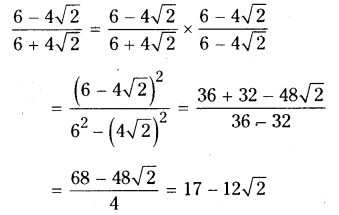
ii) √7?√5/√7+√5
Solution:
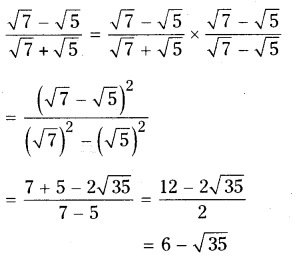
iii) 1/3√2?2√3
Solution:
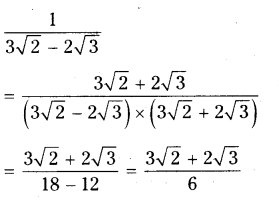
iv) 3√5?√7/3√3+√2
Solution:
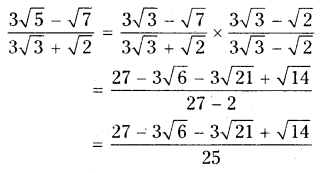
Question 7.
Find the value of √10?√5/2√2 upto three decimal places. (take √2 = 1.414, √3 = 1.732 and √5 = 2.236).
Solution:

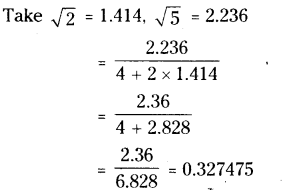
Question 8.
Find
i) 641/6
Solution:
= (26)1/6
= 6
ii) 321/5
Solution:
321/5
= (25)1/5
= 2
iii) 6251/4
6251/5
= (54)1/4
= 5
iv) 163/2
Solution:
163/2
= (42)3/2
v) 2432/5
Solution:
2432/5
= (35)2/5
vi) (46656)-1/6
Solution:
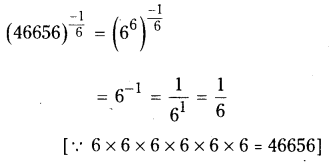
Question 9.
Simplify ∜81 ? 8 ∛343+ 15 32 + √225
Solution:
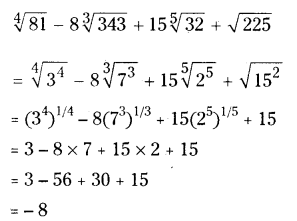
Question 10.
If ‘a’ and ‘b’ are rational numbers, find the values of a and b in each of the following equations.
i)√3+ √2/√3 - √2=a+b√6
Solution:
Given that√3+ √2/√3 - √2=a+b√6
Rationalising the denominator we get
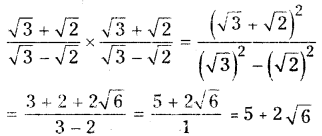
Comparing 5 + 2√6 with a + b√6
We have a = 5 and b = 2