Improve Your Learning
Question 1.
Explain the reasons for the following. (AS 1)
a) When a carpet is beaten with a stick, dust comes out of it.
Answer:
- The dust particles in the carpet are at rest.
- When the carpet is beaten with a stick, the state of rest of the dust particles is disturbed.
- Due to inertia, the dust particles comes out.
b) Luggage kept on the roof of a bus is tied with a rope.
Answer:
- Luggage kept on the roof of a bus is in the state of rest.
- As the bus moves, the luggage also moves with a velocity equal to the velocity of the bus.
- If the bus suddenly stops, the luggage resists to change its state of motion.
- Hence due to inertia it will fall down.
- To avoid this, the luggage is tied with a rope.
c) A pace bowler in cricket runs in from a long distance before he bowls.
Answer:
- When he runs in from a long distance, he gains momentum of inertia.
- Due to this larger inertia, larger force is applied in a short interval of time.
- Hence the momentum will be more.
Question 2.
Two objects have masses 8 kg and 25 kg. Which one has more inertia? Why? (AS 1)
Answer:
- The object with mass 25 kg has more inertia.
- The resistance to change the state of object will be more for a body of larger mass.
Question 3.
Keep a small rectangular shaped piece of paper on the edge of a table and place an old five rupee coin on its surface vertically as shown in the figure below. Now give a quick push to the paper with your finger. How do you explain inertia with this experiment?
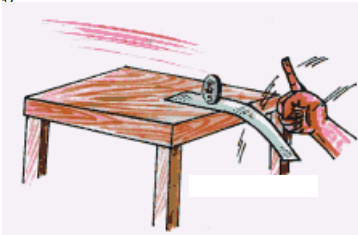
Answer:
- The coin and the paper are in inertia of rest.
- When we give a quick push to the paper, paper comes to inertia of motion and the coin remains in its original state i.e., inertia of rest.
- As a result, the paper will come out and the coin remains on the table without changing its position.
Question 4.
If a car is travelling westwards with a.constant speed of 20 m/s, what is the resultant force acting on it? (AS 1, AS 7)
Answer:
- A car is moving with a constant speed.
- Hence the net force on the car is zero both in horizontal and vertical directions.
Question 5.
What is the momentum of a 6.0 kg bowling ball with a velocity of 2.2 m/s? (AS 1)
Answer:
Mass of the ball (m) = 6.0 kg
Velocity of the ball (v) = 2.2 m/s
Momentum (p) = nv = 6.0 kg × 2.2 m/s = 13.2 kg m/s (or) 13.2 N-s
Question 6.
Two people push a car for 3 sec, with a combined net force of 200 N. (AS 1)
a) Calculate the impulse provided to the car.
Answer:
Fnet= 200 N ; ∆t =3 sec
Impulse ∆p = Fnet. ∆t = 200 × 3 = 600 N - sec.
b) If the car has a mass of 1200 kg, what will be its change in velocity?
Answer:
Mass of the car (m) = 1200 kg.; Net force (Fnet) = 200 N
Time ∆t = 3 sec. ; Change in velocity ∆v =?
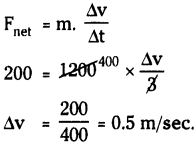
Question 7.
What force is required to produce an acceleration of 3 m/sec2 in an object of mass 0.7 kg? (AS 1)
Answer:
Mass of the object (m) = 0.7 kg.; Acceleration (a) = 3 m/sec2
Force required (F) = ?
F = ma = 0.7 x 3 = 2.1 N
Question 8.
A force acts for 0.2 sec on an object having mass 1.4 kg initially at rest. The force stops to act but the object moves through 4 m in the next 2 seconds, find the magnitude of the force. (AS 1)
Answer:
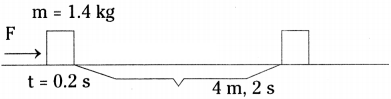
Velocity after 0.2 sec v = u + at = 0 + 0.2 a = 0.2a ……….. (1)
After 0.2 s, the body moves with uniform velocity, acceleration is zero, because force is removed.
∴ Velocity v =s/t=4/2=2 m/s. ………. (2)
From (1) & (2)
v = 0.2a ⇒ 2 = 0.2a
⇒ a =2/0.2= 10 m/s2
∴ Force applied F = ma = 1.4 kg × 10 m/s2 = 14 N.
Question 9.
An object of mass 5 kg is moving with a velocity of 10 ms-1. A force is applied so that in 15 s, it attains a velocity of 25 ms-1. What is the force applied on the object? (AS 1)
Answer:
Mass (m) = 5 kg ; Initial velocity (u) = 10 m/s.; Time (t) = 15 s
Final velocity (v) = 25 m/s.
Acceleration a = =v?u/t=25?10/15=15/15=1 m/s2 .
Force applied on the object F = ma = 5 × 1=5 N.
Question 10.
Find the acceleration of body of mass 2 kg from the figures shown. (AS 1)
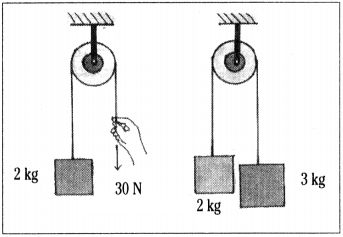
Answer:
1) Force 30 N is acting downwards on weight of (2 × 10) = 20 kg.
The acceleration a = 30?20/2=10/2 = 5 m/s2
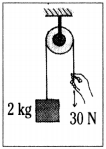
2) m1 = 2 kg, m2 = 3 kg.
m2 pulls the body mt with a weight 3 × 10 = 30 N.
∴ Acceleration of m1 = 30?20/3+2=10/5
= 2 m/s2.
Question 11.
Take some identical marbles. Make a path or a track keeping your notebooks on either side so as to make a path in which marbles can move. Now use one marble to hit the other marbles. Take two, three marbles and make them to hit the other marbles. What can you explain from your observations? (AS 5)
Answer:
- When one marble is hit by another marble, both the marbles move with some velocity.
- When the marble is hit by two, three marbles, all marbles move with a velocity which is more than in the previous case.
- As we are hitting with more marbles, the mass increases. So that the net momentum also increases.
Question 12.
A man of mass 30 kg uses a rope to climb which bears only 450 N. What is the maximum acceleration with which he can climb safely? (AS 1, AS 7)
Answer:
Mass m = 30 kg. ; Force F = 450 N
Acceleration a = ?
F = ma
∴ a = F/m=450/30 =15 m/sec2
∴ The required acceleration =15 m/sec2
Question 13.
An vehicle has a mass of 1500 kg. What must be the force between the vehicle and the road if the vehicle is to be stopped with a negative acceleration of 1.7 m/sec2? (AS 1, AS 7)
Answer:
Mass of the vehicle, m = 1500 kg.; Acceleration (-a) = 1.7 m/sec2
Force, F =?
F = m (-a) = 1500 × (-1.7) = ( - ) 2550 N
∴ The force between the vehicle and road is 2550 N, in the direction opposite to that of the vehicle.
Question 14.
If a fly collides with the windshield of a fast moving bus, is the impact force experienced, same for the fly and the bus? Why? (AS 1, AS 2)
Answer:
The impact force experienced by the fly will be more, because the mass of fly is negligible when compared to the mass of the bus.
Question 15.
A truck is moving under a hopper with a constant speed of 20 m/sec. Sand falls on the truck at a rate 20 kg/s. What is the force acting on the truck due to falling of sand? (AS 1, AS 7)
Answer:
Mass of the sand falling on the truck in 1 sec = 20 kg
Constant speed of the truck = 20 m/s
Acceleration in 1 sec, a = Δv/Δt=20/1 = 20 m/sec2
Force applied on the truck, F = ma = 20 kg x 20 m/sec2 = 400 N
Question 16.
Two rubber bands stretched to the standard length cause an object to accelerate at 2 m/sec2. Suppose another object with twice the mass is pulled by four rubber bands stretched to the standard length. What is the acceleration of the second object? (AS 1)
Answer:
First object:
Let the force applied by two rubber bands = F1Newton
Mass of the object = m1kg; Acceleration a1= 2 m/sec2
We know F = ma
F1= m1× 2
⇒F1= 2m1…….(1)
Second object:
The force applied by 4 rubber bands = 2F1Newton
Mass of the object = 2m1kg ; Acceleration a2=?
We know F = ma
2F1= 2m1. a2
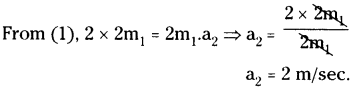
∴ Acceleration of the second object = 2 m/sec²
Question 17.
Illustrate an example of each of the three laws of motion. (AS 1)
Answer:
First law of motion :
A body continues its state of rest or of uniform motion unless a net force acts on it.
Ex:
- When the bus which is at rest begins to move suddenly, the person standing in the bus falls backward.
- When you are travelling in bus, the sudden stop of the bus makes you fall forward.
Second law of motion :
The rate of change of momentum of a body is directly proportional to the net force acting on it and it takes place in the direction of net force.
Ex : Place a ball on the veranda and push it gently. Then the ball accelerates from rest. Thus, we can say that force is an action which produces acceleration.
Third law of motion :
If one object exerts a force on the other object, the second object exerts a force on the first one with equal magnitude but in opposite direction.

Ex :
- When birds fly, they push the air downwards with their wings, and the air pushes back the bird in opposite upward direction.
- When a fish swims in water, the fish pushes the water back and the water pushes the fish with equal force but in opposite direction.
- A rocket accelerates by expelling gas at high velocity. The reaction force of the gas on the rocket accelerates the rocket in a direction opposite to the expelled gases.
Question 18.
Two ice-skaters initially at rest, push of each other. If one skater whose mass is 60 kg has a velocity of 2 m/s. What is the velocity of other skater whose mass is 40 kg? (AS 1, AS 7)
Answer:
Mass of first skater m1= 60 kg.;
Velocity of first skater v1= 2 m/s.
Mass of second skater m2= 40 kg.; Velocity of second skater v2=?
As the two skaters push each other, the resultant momentum will become zero.
The resultant momentum m1v1+ m2v2= 0
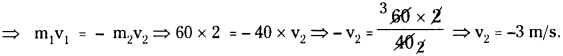
∴ Velocity of second skater is 3 m/s, but in the direction opposite to the first skater.
Question 19.
A passenger in moving train tosses a coin which falls behind him. It means that the motion of the train is (AS 7)
a) Accelerated
b) Uniform
c) Retarded
d) Circular motion
Answer:
a) Accelerated
Question 20.
A horse continues to apply a force in order to move a cart with a constant speed. Explain. (AS 1)
Answer:
- The cart moves when the force (in the form of pulling) is applied by the horse.
- As the horse and cart are moving, the net momentum will be zero at any instance of time.
- Hence when the horse comes to rest, the cart also comes to rest.
- To avoid this and to move the cart with a constant speed, the horse must apply force continuously.
Question 21.
A force of 5 N produces an acceleration of 8 m/sec2 on a mass m, and an acceleration of 24 m/sec2 on a mass m2. What acceleration would the same force provide If both the masses are tied together? (AS
1)
Answer:
For the first mass (m1)
Force F = 5 N
Acceleration a = 8 m/s2
We know, F = ma
5 = m, . 8
m1=5/8 kg
For the second mass (m2)
Force F = 5 N
Acceleration a = 24 m/sec2
We know, F = ma
5 = m2.24
m2=5/24 kg
When both the masses are tied together and the same force is applied, then
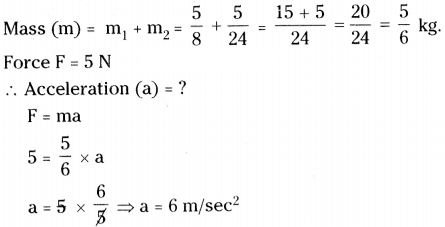
Question 22.
A hammer of mass 400 g, moving at 30 m/s, strikes a nail. The nail stops the hammer in a very short time of 0.01 s. What is the force of the nail on the hammer? (AS 1)
Answer:
Mass of the hammer (m) = 400 g = 0.4 kg. ; Velocity of the hammer (v) = 30 m/s.
Momentum (∆p) = 30 × 0.4 N - s.
The nail stops the hammer with in a time 0.01 s.
∴ ∆t = 0.01 s.
The stopping force of the nail on the hammer.
Question 23.
System is shown in figure. Assume there is no friction. Find the acceleration of the liloc-ks-and tension in the string. Take g = 10 m/s2; (AS 1)
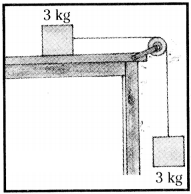
Answer:
m1= 3 kg, m2= 3 kg.
1) Acceleration ’a’ and tension T on m1are shown in figure.
2) Acceleration a and tension T will be as shown in figure.
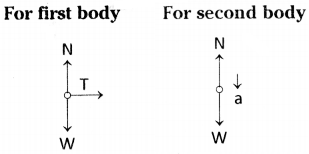
Normal force = weight 3s - T = 3a ………… (2)
∴ only tension applied
Tension T = 3 kg × a = 3a
From (1) & (2)
3g - 3a = 3a ⇒ 3g = 6a ⇒ a =3g/6=3×10/6= 5 m/s2.
Tension T = 3a = 3 × 5 = 15 N.
Question 24.
Three identical blocks, each of mass 10 kg, are pulled as shown on the hoii ;ontal frictionless surface. If the tension (F) in the rope is 30 N, what is the acceleration oi each block? And what are the tensions in the other ropes? (Neglect the masses of the ropes) (AS 1)
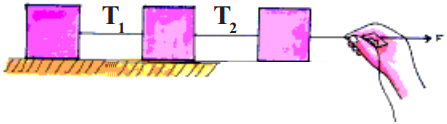
Answer:
Three blocks, each of mass 10 kg are pulled by a rope.
∴ Total mass = 10 + 10 + 10 = 30 kg
Force applied by the rope, F = 30 N
∴ Acceleration of each block, a =F/m=30/30= 1 m/sec2.
Tension in first rope (T1)
First rope pulls only one block whose mass is 10 kg with an acceleration 1 m/sec2.
∴ F = ma = 10 kg × 1 m/sec2= 10 N
Tension in second rope (T2)
Second rope pulls two blocks, each of mass 10 kg.
∴ Total mass = 10 + 10 = 20 kg.
Acceleration, a = 1 m/sec2
Force, F = ma = 20 × 1 = 20 N
Question 25.
Divya observed a horse pulling a cart. She thought that cart also pulls the horse with same force in opposite direction. As per third law of motion, the cart should not move forward. But her observation of moving cart raised some questions in her mind. Can you guess what questions are raised in her mind? (AS 2)
Answer:
- According to Newton’s third law, when horse pulls a cart, the cart also pulls the horse with same force but in opposite direction. So the cart has to stop. Why is the cart moving?
- What is the effect of friction of ground on the cart and horse?
- Does the cart continue to move even if the horse stops pulling it?
- What makes the cart to move continuously?
- Does it become an isolated system?
- What is the action and reaction in this system?
Question 26.
How do you appreciate Galileo’s thought of “any moving body continues in the stale only until some external force acts on it”, which is contradiction to the Aristotle’s belief of “any moving body naturally comes to rest”? (AS 6)
Answer:
- Science is dynamic.
- All theories can change time to time so that the science and technology will be developed.
- Aristotle’s belief proved to be wrong only by the experiments conducted by Galileo.
- So anybody can challenge the existing theories with proper experimentation.
- Aristotle’s and Galileo’s contradictory thought lead Newton to propose most popular laws of motion.
- Newton’s third law of motion is the basic principle in rocket launching.
- Nowadays we are enjoying the results of satellites launched by rockets.
- Hence comfortable life is the effort on experiments, theories, and calculations made by scientists with a zeal to invent new.