Improve Your Learning
Question 1.
Define work and write its units. (AS 1)
Answer:
Work : Work can be defined as the product of the force (F) and the distance (s) moved along the direction of the force.
Work done = Force × displacement = F × s
- Work is a scalar quantity.
- Unit of work is ‘N – m’ or ‘Joule’ (J).
Question 2.
Give few examples where displacement of an object is in the direction opposite to the force acting on the object. (AS 1)
Answer:
- When a ball is thrown up, the motion is in upward direction, whereas the force due to earth’s gravity is in downward direction.
- If a ball is moving on plain ground, will get stopped after sometime, due to frictional force acting on it in opposite direction.
Question 3.
Identify the wrong statement among the following. Rewrite them by making necessary corrections. (AS 1)
a) Work and energy have different units.
Answer:
Correction :
Work and energy have same units.
b) When an aeroplane takes off, the work done by its weight is positive.
Answr:
Correction : When an aeroplane takes off, the work done by its weight is negative.
c) The potential energy of spring increases when it is extended and decreases when it is compressed.
Answer:
Correct.
d) If the work done by external forces on a system is negative then the energy of the system decreases.
Answer:
Correct.
e) When a body is falling freely from a height, its kinetic energy remains constant.
Answer:
Correction : When a body is falling freely from a height, its K.E. increases and P.E. decreases, but the total energy of the body remains constant.
f) The unit of power is watt.
Answer:
Correct.
Question 4.
What is mechanical energy? (AS 1)
Answer:
The sum of the kinetic energy and the potential energy of an object is called its mechanical energy.
Question 5.
State the principle of conservation of energy. (AS 1)
Answer:
Energy can neither be created nor destroyed. It can only be changed from one form to another.
Question 6.
When you lift a box from the floor and put it on an almirah the potential energy of the box increases but there is no change in its kinetic energy. Is it violation of conservation of energy? Explain. (AS 7)
Answer:
- When the box is on the floor, it has no K.E., but has some P.E.
- Its P.E. increases as it is lifted and put on an almirah.
- In this event, the energy produced by the person converts into K.E. and the total M.E. remains same.
- Hence it is not the violation of conservation of energy.
Question 7.
One person says that potential energy of a particular book kept in an almirah is 20 J and other says it is 30 J. Is one of them necessarily wrong? Give reasons. (AS 2, AS 1)
Answer:
Two cases will arise in this situation.
Case – I :
One of them will be wrong, if both of them kept the book in the same shelf of the almirah.
Case – II :
Both of them will be correct, if the first person keeps the book in lower shelf and the second one keeps the book in upper shelf of the almirah.
Question 8.
In which of the following cases is the work done positive or zero or negative? (AS 1)
a) Work done by the porter on a suitcase in lifting it from the platform on to his head.
Answer:
Positive
b) Work done by the force of gravity on suitcase as the suitcase falls from porter’s head.
Answer:
Positive
c) Work done by the porter standing on platform with suitcase on his head.
Answer:
Zero
d) Work done by force of gravity on a ball thrown up vertically up into the sky.
Answer:
Negative
e) Work done by force applied by hands of a man swimming in a pond.
Answer:
Negative
Question 9.
What is potential energy? Derive an equation for gravitational potential energy of a body of mass ‘m’ at a height ‘h’. (AS 1)
Answer:
Potential energy:
The energy possessed by an object because of its position or shape is called its potential energy.
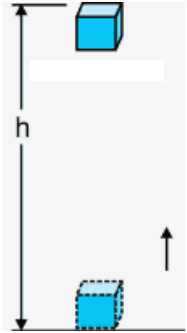
Potential energy of a body at height (Or) Gravitational potential energy :
- The gravitational potential energy of an object at a point above the ground is defined as the work done in raising it from the ground to that point against gravity.
- Consider an object of mass ‘m’ raised to height ’h’ from the ground.
- A force is required to do this.
- The minimum force required to raise the object is equal to the weight of the object (mg).
- The object gains energy equal to the work done on it.
- Let the work done on the object against gravity be ‘W’.
∴ W = Force × displacement
= mg × h
W = mgh
- The object gains the energy equal to the mgh’ units.
- This energy is the potential energy of the object at a height ‘h’.
∴ P.E. = mgh
Question 10.
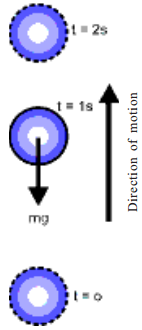
When an apple falls from a tree what happens to its gravitational potential energy just as it reaches the ground? After it strikes the ground? (AS 7)
Answer:
- Let us imagine an apple of mass ‘m’ falls from a height h.
- Before starting to fall down, its velocity is zero. Hence its energy is purely potential.
- When it falls down, its gravitational potential energy gradually converts into kinetic energy, but the entire energy in the system remains same.
- When it strikes the ground, its energy is fully kinetic, till its velocity becomes zero.
Question 11.
Let us assume that you have lifted a suitcase and kept it on a table. On which of the following does the work done by you depend or not depend? Why?
a) The path taken by the suitcase
b) The time taken by you in doing so
c) The weight of the suitcase
d) Your weight
Answer:
We know that P.E. = mgh
a) The work done by you does not depend on the path taken by the suitcase, because the height from the ground to the top of the table is fixed in this case, (h constant)
b) The work done by you does not depend the time taken, in doing so, because the work done is same. If you take less time your power will be more otherwise the power is less.
c) The work done by you depends on the weight of the suitcase. As the weight of the suitcase increases, the work done will also increase (See the formula P.E. = mgh).
d) The work done by you depends on your weight, we know that a person with more weight can Mft the suitcase easily.
Question 12.
When you push your bicycle up an incline, the potential energy of the bicycle and yourself increase. Where does this energy come from? (AS 7)
Answer:
The energy inside our body causes increase in the P.E. of the bicycle and ourself.
As we are pushing the bicycle upon incline, the work done by the gravitational force is negative. Hence the energy loses.
Question 13.
Why does a person standing for a long time get tired when he does not appear to be doing any work? (AS 7)
Answer:
1) A person standing for a long time, does not appear to be doing any work, because there is no displacement.
2) Eventhough work has not been done, the person gets tired.
3) This is due to the utilization of energy produced in his body.
Question 14.
What is kinetic energy? Derive an expression for the kinetic energy of a body of mass ‘m’ moving at a speed ‘v’. (AS 1)
Answer:
Kinetic energy :
The energy possessed by an object due to its motion is called kinetic energy.
Numerical expression for K.E.:
1) Let us assume that an object of mass (m) is at rest on a smooth horizontal plane as shown in figure.
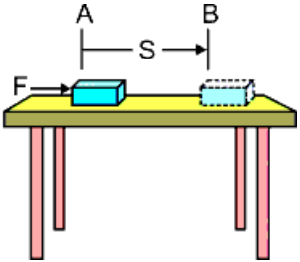
2) Let be displaced through a distence ‘s’ from the point A to B by a force (F) acting upon it in the direction of the displacement.
3) In the horizontal direction the net force ‘Fnet‘ is equal to the force applied ‘F’.
∴ W = Fnet.s = F.s …………. (1)
4) Let the work done on the object cause a change in its velocity from ‘u’ to ‘v’ anr the ‘acceleration produced be ‘a’.
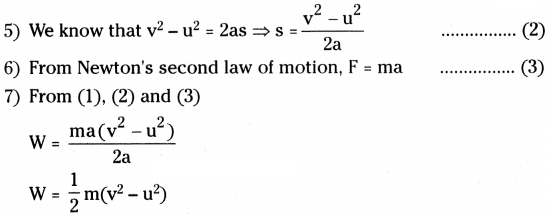
8) As we Have assumed that object is at rest, then the initial velocity u = 0.
∴ W = 12 mv2
9) We know that K.E. of a body moving with certain velocity is equal to work done on the object to acquire that velocity from rest.
10) Thus the K.E. of an object of mass’m’ and moving with velocity V is equal to
K.E =1/2mv2
Question 15.
A free-fall object eventually stops on reaching the ground. What happens to its kinetic energy? (AS 1)
Answer:
- Its kinetic energy becomes ‘zero’.
- As the ball stops on reaching the ground, its final velocity ‘v’ becomes zero.
- Hence the K.E. =1/2 mv2 =1/2.m.0 = 0
Question 16.
A man carrying a bag of total mass 25 kg climbs up to a height of 10 m in 50 seconds. Calculate the power delivered by him on the bag. (AS 1)
Answer:
Mass of the bag = 25 kg ; Height ‘h’ = 10 m
Acceleration due to gravity g = 9.8 m/s2
The P.E. of the man = mgh = 25 × 9.8 × 10 = 2450 J
The work done by the man is equal to the P.E. possessed by the man.
∴ The work done by the man (W) = 2450 J ; Time (t) = 50 sec.
∴ Power delivered by the man on the bag = Wt=2450 J50sec = 49 watts
Question 17.
A 10 kg ball is dropped from a height of 10 m. Find (a) the initial potential energy of the ball, (b) the kinetic energy just before it reaches the ground and (c) the speed just before it reaches the ground.
Answer:
Mass of the ball = 10 kg ; It is dropped from a height h = 10 m
Acceleration due to gravity g = 9.8 m/sec2
a) The initial P.E. of the ball = mgh = 10 × 9.8 × 10 = 980 J
b) We know that the energy is conserved in a freely falling object at anywhere in its journey.
∴ The K.E. just before it reaches the ground = 980 J
c) K.E. just before it reaches the ground = 980 J ;
Speed = v m/s
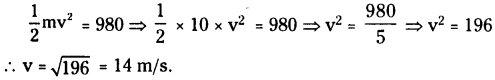
Question 18.
Calculate the work done by a person in lifting a load of 20 kg from the ground and placing it 1 m high on a table. (AS 1)
Answer:
Mass of a load = 20 kg ; Height h = 1 m
Acceleration due to gravity = 9.8 m/s2
The work done by a person in lifting the load is equal to the P.E.
P.E. = mgh = 20 × 9.8 × 1 = 196 J
Question 19.
Find the mass of a body which has 5 J of kinetic energy while moving at a speed of 2 m/s. (AS 1)
Answer:
KE = 5 J
Speed v = 2 m/sec
Mass of the body = m kg.
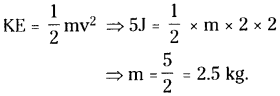
Question 20.
A cycle together with its rider weighs 100 kg. How much work is needed to set it moving at 3 m/s?
Answer:
Mass of the bicycle with its rider = 100 kg ; Speed = 3 m/s Amount of work needed to set it moving is equal to its K.E.
K.E. = 1/2 mv2 = 12 × 100 × 3 × 3 = 450 J
∴ 450 J work is needed.
Question 21.
When the speed of a ball is doubled its kinetic energy (AS 1)
A) remains same
B) gets doubled
C) becomes half
D) becomes 4 times
Answer:
D) becomes 4 time
Question 22.
Two bodies of unequal masses are dropped from the top of a building. Which of the following is equal for both bodies at any instant?
A) Speed
B) Force of gravity
C) Potential energy
D) Kinetic energy
Answer:
B) Force of gravity
Question 23.
A man with a box on his head is climbing up a ladder. The work done by the man on the box is ……….
A) Positive
B) Negative
C) Zero
D) Undefined
Answer:
A) Positive
Question 24.
A porter with a suitcase on his head is climbing up steps with uniform speed. The work done by the “weight of the suitcase” on the suitcase is ……
A) Positive
B) Negative
C) Zero
D) Undefined
Answer:
B) Negative
Question 25.
How will the increasing energy needs and conservation of energy influence international peace, cooperation and security? Discuss.
Answer:
1) The increasing energy needs and conservation of energy influence international peace, co-operation and security.
2) For example, many great nations depend on the gulf countries and many countries for fuel (Petrol, diesel, etc.). The need of fuel brings co-operation among the countries. Also the need of energy (electricity, fuel, etc.) link all nations to a small circle so that there comes the peace, co-operation and security.
3) Atomic energy, thermal energy, chemical energy, etc. bring unity among all nations.
Question 26.
How would you assess the role of energy conversion occurring naturally in maintaining ecological balance of nature?
Answer:
- The chemical changes in the sun is providing us the heat energy and light energy to the earth.
- The heat energy of the sun evaporates the water into water vapour. This helps us to get heavy rainfall.
- The solar energy is taken by the plant to change CO2, water and chloroplast into starch which is the food of the plant. This process is called photosvnthesis.
- In the photosynthesis process the plant releases O2 (oxygen).
- The leguminous (Pea plants) plants help the bacteria present at their roots. In return they help the plants to fix nitrogen in them The nitrogen cycle is maintained.
- From the above examples we can understand that the energy conversion is helpful in maintaining ecological balance of nature.
Question 27.
Collect pictures showing various situation where potential energy possessed by an object depends on its shape and position. Prepare a scrap book.
Answer:
Note : Students can collect pictures of different objects at different heights, with different shapes.
e.g.: 1) A stone on a hill.
2) A book on a table and a pen on a table, etc.
Paste these pictures in your scrap book.
Question 28.
Draw a diagram to show conservation of mechanical energy in case of free falling body.
Answer: