Question 1.
In the given figure, name:
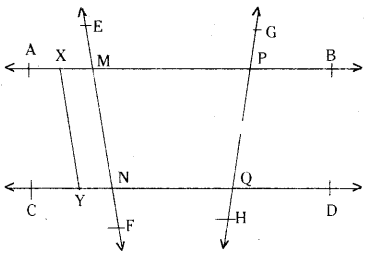
i) Any six points
Solution:
A, B, C, D, P, Q, M, N etc.
ii) Any five line segments
Solution:

iv) Any four lines
Solution:

Question 2.
Observe the following figures and identify the type of angles in them.
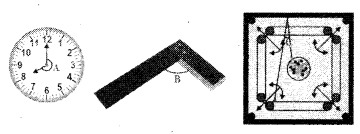
Solution:
∠A - reflex angle
∠B - right angle
∠C - acute angle
Question 3.
State whether the following state¬ments are true or false
i) A ray has no end point.

iv) A line has a definite length. - False
v) A plane, has length and breadth but no thickness. - True
vi) Two distinct points always determine a unique line. - True
vii) Two lines may intersect in two points. - False
viii) Two intersecting lines cannot both be parallel to the same line. - True
Question 4.
What is the angle between two hands of a clock when the lime in the clock
is
a) 9 ‘o clock
b) 6 ‘o clock
c) 7 ; 00 p.m.
Solution:
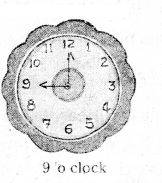
a) 12 hours = = 360°
1 hour =360°/12 = 30°
∴Angle between hands when the time is 9 o clock = 3 x 30 = 90
b)
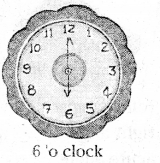
Angle between hands = 6 x 30° = 180°
c)

Angle between hands = 7 x 30° = 210°

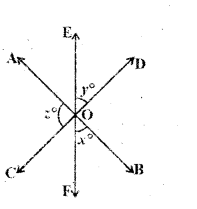
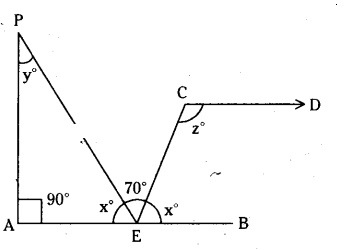
Solution:
From the figure
2x + 2y + 2z = 360°
⇒ x + y + z = 180°
x : y : z = 2 : 3 : 5
Sum of the terms of the ratio
= 2 + 3 + 5 = 10
Question 2.
Find the value of x in the following figures.
i)
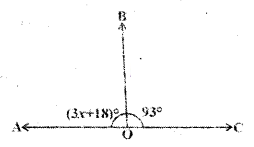
Solution:
From the figure
3x + 18= 180° - 93° (∵ linear pair )
3x + 18 = 87
3x = 87- 18 = 69
∴ x = 69/3 = 23
ii)
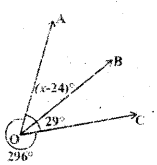
Solution:
From the figure
(x - 24)° + 29° + 296° = 360"
(∵ complete angle)
x + 301° = 360°
∴ x = 360° - 301° = 59°
iii)
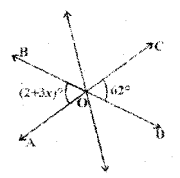
Solution:
From the figure
2 + 3x = 62
(∵ vertically opposite angles)
3x = 62 - 2
∴ 3x = 60° ⇒ x = 60/3
∴ x = 20°
iv)
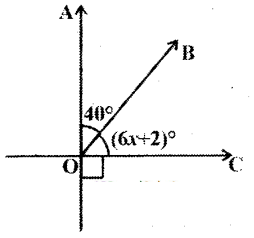
Solution:
From the figure
40 + (6x + 2) = 90°
(∵ complementary angles)
6x = 90° - 42°
6x = 48
x = 48/6= 8°

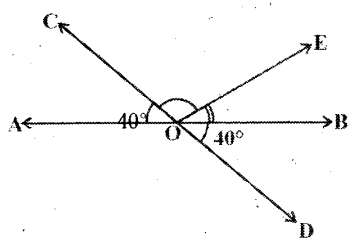
Solution:
Given that ∠AOC +∠BOE = 70°
∠BOD = 40°
∠AOC = 40°
(∵ ∠AOC, ∠BOD are vertically opposite angles)
∴ 40° + ∠BOE = 70°
⇒ ∠BOE = 70° - 40° = 30°
Also ∠AOC + ∠COE +∠BOE = 180°
( ∵ AB is a line)
⇒ 40° + ∠COE + 30° = 180°
⇒ ∠COE = 180° -70° = 110°
∴ Reflex ∠COE = 110°

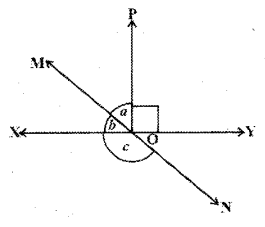
Solution:
Given that XY and MN are lines.
∠POY = 90°
a : b = 2 : 3
From the figure a + b = 90°
Sum of the terms of the ratio a : b
= 2 + 3 = 5
∴ b = 3/5 x 90° = 54°
From the figure b + c = 180°
(∵ linear pair of angles)
54° + c = 180°
c = 180°-54° = 126°
Question 5.
In the given figure ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
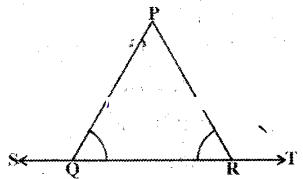
Solution:
Given that ∠PQR = ∠PRQ
From the figure
∠PQR + ∠PQS = 180° ...... (1)
∠PRQ + ∠PRT = 180° ......(2)
From (1) and (2)
∠PQR + ∠PQS = ∠PRQ + ∠PRT
But ∠PQR = ∠PRQ
So ∠PQS = ∠PRT
Hence proved.
Question 6.
In the given figure, if x + y = w + z, then prove that AOB is a line.
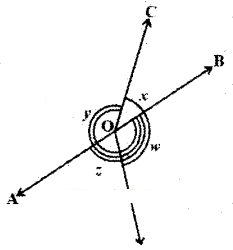
Solution:
Given that x + y = w + z = k say
From the figure
x + y + z + w = 360°
(∵ Angle around a point)
Also x + y = z + w
∴ x + y = z + w = 360°/2
∴ x + y = z + w = 180°
OR
k + k = 360°
2k = 360°
k = 360/2
(i.e.) (x,y) and (z, w) are pairs of adjacent angles whose sum is 180°.
In other words (x, y) and (z, w) are linear pair of angles ⇒ AOB is a line.

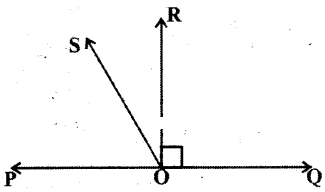
Solution:
Given : OR ⊥ PQ ? ∠ROQ = 90°
To prove: ∠ROS = 1/2(∠QOS - ∠POS)
Solution:
Proof: From the figure
∠ROS = ∠QOS - ∠QOR .....(1)
∠ROS = ∠ROP - ∠POS .......(2)
Adding (1) and (2)
∠ROS + ∠ROS = ∠QOS - ∠QOR +∠ROP - ∠POS [ ∵ ∠QOR = ∠ROP = 90° given]
⇒ 2∠ROS = ∠QOS - ∠POS
⇒ ∠ROS = 1/2[∠QOS - ∠POS]
Hence proved.

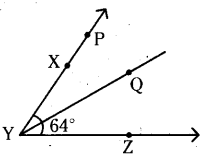
∠XYQ = 32°
∠QYP = 32°
Question 1.
It is given that l // m; to prove ∠1 is supplement to ∠8. Write reasons for the Statements.
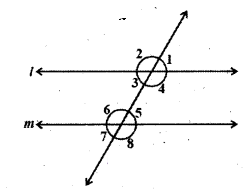
Solution:
| Statement |
Reasons |
| i) l //m |
∠1 + ∠8 = 180° (exterior angles on the same side of the transversal) |
| ii) ∠1 = ∠5 |
corresponding angles |
| iii) ∠5 + ∠8 = 180° |
linear pair of angles |
| iv) ∠1 + ∠8 = 180° |
exterior angles on the same side of the transversal. |
| v) ∠1 is supplement is ∠8 |
exterior angles on the same side of the transversal. |
Question 2.
In the given figure AB ‖ CD; CD ‖ EF and y: z = 3:7 find x.
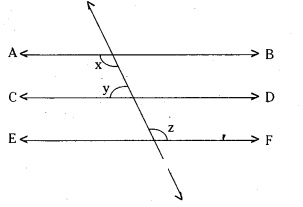
Solution:
Given that AB//CD; CD//EF.
⇒ AB // EF
Also y : z = 3 : 7
From the figure x + y = 180 ..... (1)
[∵ interior angles on the same side of the transversal]
Also y + z = 180 ...... (2)
Sum of the terms of the ratio y : z
= 3 + 7 = 10
∴ y = 3/10 x 180° = 54°
y = 7/10 x 180° = 126°
From (1) and (2)
x + y = y + z
⇒ x = z = 126°
Question 3.
In the given figure AB//CD; EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
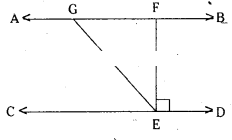
Solution:
Given that EF ⊥ CD; ∠GED = 126°
i. e., ∠FED = 90° and
∠GEF = ∠GED - ∠FED
∠GEF = 126° - 90° = 36°
In ∆GFE
∠GEF + ∠FGE + ∠EFG = 180°
36 + ∠FGE + 90° = 180°
∠FGE = 180° - 126° = 54°
∠AGE = ∠GFE + ∠GEF
(exterior angle in ∆GFE)
= 90°+ 36°= 126°
Question 4.
In the given figure PQ//ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS. [Hint : Draw a line parallel to ST through point R.]
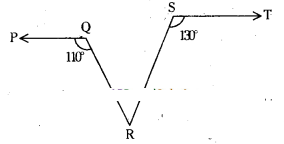
Solution
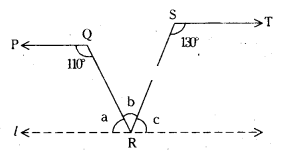
Given PQ // ST
Draw a lipe l parallel to ST through R.
From the figure
a + 110° = 180° and c + 130 = 180°
[ ∵ Interior angles on the same side of the transversal]
∴ a = 180° -110° = 70°
c = 180° - 130° = 50°
Also a + b + c = 180° (angles at a point on a line)
70° + b + 50° = 180°
b = 180° - 120° = 60°
∴ ∠QRS = 60°
Question 5.
In the given figure m // n. A, B are any two points on in and n respectively. Let C be an interior point between the lines m and n. Find ∠ACB.
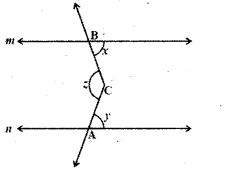
Soloution
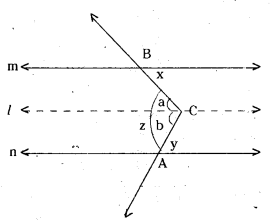
Draw a line l parallel to m and n through C.
From the figure
x = a [ ∵ alternate interior angles for l, m]
y = b [ ∵ alternate interior angles for l, n]
∴ z = a + b = x + y
Question 6.
Find the values of a and b, given that p // q and r // s.
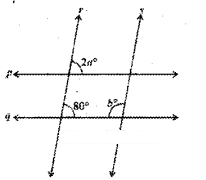
Solution:
Given that p // q and r // s.
∴ From the figure
2a = 80° (∵ corresponding angles)
a = 80°/2 = 40°
Also 80° + b = 180° ( ∵ interior angles on the same side of the transversal)
∴ b = 180° - 80° = 100°
Question 7.
If in the figure a // b and c // d, then name the angles that are congruent to (i) ∠1 and (ii) ∠2.
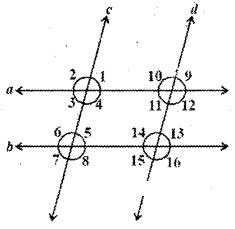
Solution:
Given that a // b and c // d.
∠1 = ∠3 (∵ vertically opposite angles)
∠1 = ∠5 (∵ corresponding angles)
∠1 = ∠9 (∵ corresponding angles)
Also ∠1 = ∠3 = ∠5 = ∠7 ;
∠1 = ∠11 = ∠9 = ∠13 = ∠15
Similarly ∠2 = ∠4 = ∠6 = ∠8
Also ∠2 = ∠10 = ∠12 = ∠14 = ∠16
Question 8.
In the figure the arrow head segments are parallel, find the values of x and y.
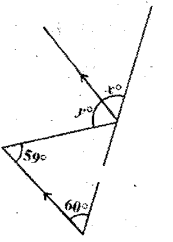
Solution:
From the figure
y = 59° ( ∵ alternate interior angles)
x = 60° ( ∵ corresponding angles)
Question 9.
In the figure the arrow head segments are parallel then find the values of x and y.
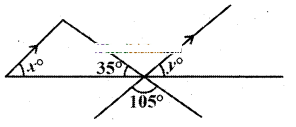
Solution:
From the figure 35° + 105° + y = 180°
∴ y = 180° - 140°
= 40°
∴ x = 40° (∵ x, y are corresponding angles)
Question 10.
Find the values of x and y from the figure.
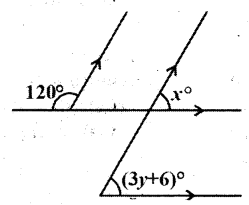
Solution:
From the figure 120° + x = 180°
(∠ exterior angles on the same side of the transversal)
∴ x = 180° - 120°
x = 60°
Also x = (3y + 6)
(∵ corresponding angles)
3y + 6 = 60°
3y = 60° - 6° = 54°
y = 54/3 = 18°
∴ x = 60°; y = 18°
Question 11.
From the figure find x and y.
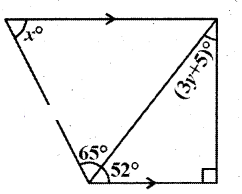
Solution:
From the figure
52° + 90° + (3y + 5)° = 180°
(∵ interior angles of a triangle)
∴ 3y + 147 = 180°
⇒ 3y = 33°
⇒ y = 33/3 = 11°
Also x + 65° + 52° = 180°
(∠ interior angles on the same side of the transversal)
∴ x = 180° -117° = 63°
Question 12.
Draw figures for the following statement.
“If the two arms of one angle are respectively perpendicular to the two arms of another angle then the two angles are either equal or supplementary
Solution:
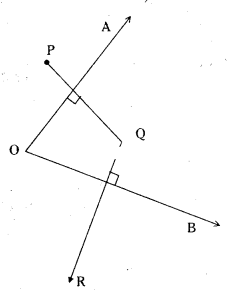
AO ⊥ PQ, OB ⊥ QR
Angles are supplementary.
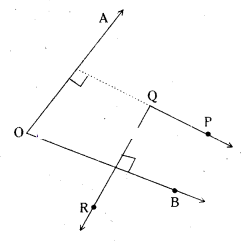
AO ⊥ PQ, OB ⊥ QR
Angles are equal.
Question 13.
In the given figure, if AB // CD; ∠APQ = 50° and ∠PRD = 127°, find x and y.
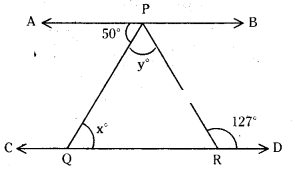
Solution:
Given that AB // CD.
∠PRD = 127°
From the figure x = 50°
(∵ alternate interior angles)
Also y + 50 = 127°
(∵ alternate interior angles)
∴ y = 127-50 = 77°

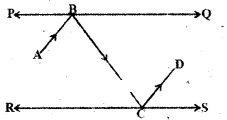
Solution


Question 15.
In the figures given below AB // CD. EF is the transversal intersecting AB and CD at G and H respectively. Find the values of x and y. Give reasons.
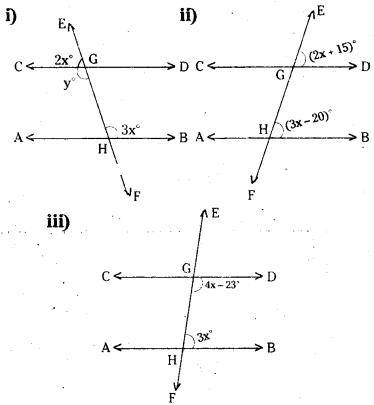
Solution:
For fig(i)
3x = y (∵ alternate interior angles)
2x + y = 180° (∵ linear pair of angles)
∴ 2x + 3x = 180°
5x= 180°
x = 180/5 = 36°
and y = 3x = 3 x 36 = 108°
For fig (ii)
2x + 15 = 3x- 20°
(∠ corresponding angles)
2x-3x = -20-15
- x = - 35
x = 35°
For fig (iii)
(4x - 23) + 3x = 180°,
( ∵ interior angles on the same side of the transversal)
7x- 23 = 180°
7x = 203
x = 203/7= 29°
Question 16.
In the given figure AB // CD, ‘t’ is a transversal intersecting E and F re-spectively. If ∠2 : ∠1 = 5 : 4, find the measure of each marked angles.
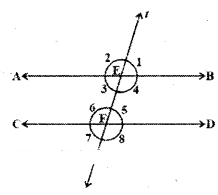
Solution:
Given that AB // CD and ∠2 : ∠1 = 5 : 4 ∠1 + ∠2 = 180° (-. linear pair of angles) Sum of the terms of the ratio ∠2 :∠1 = 5 + 4 = 9
∴ ∠1 = 4/9 x 180° = 80°
∠2= 5/9x 180° = 100°
Also ∠1, ∠3, ∠5, ∠7 are all equal to 80°. Similarly ∠2, ∠4, ∠6, ∠8 are all equal to 100°.
Question 17.
In the given figure AB//CD. Find the values of x, y and z.
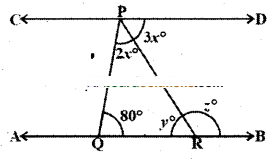
Solution:
Given that AB // CD.
From the figure (2x + 3x) + 80° = 180°
(∵ interior angles on the same side of the transversal)
∴ 5x = 180° - 80°
x = 100/5= 20°
Now 3x = y (∠ alternate interior angles)
y = 3 x 20° = 60° .
And y + z = 180°
(∵ linear pair of angles)
∴ z = 180°-60° = lg0°
Question 18.
In the given figure AB // CD. Find the values of x, y and z.
Solution:
Given that AB // CD.
From the figure x° + 70° + x° = 180°
(∵ The angles at a point on the line)
∠ 2x = 180° - 70°
x = 110°/2= 55-
Also 90° + x° + y° = 180°
[∵ interior angles of a triangle]
90° + 55° + y = 180°
y = 180° - 145° = 35°
And x° + z° = 180°
[∵ interior angles on the same side of a transversal]
55° + z = 180°
z = 180°-55° = 125°
Question 19.
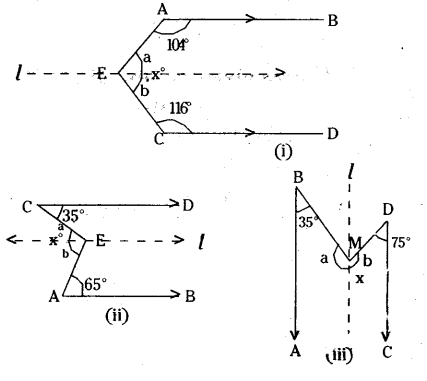
In each of the following figures AB // CD. Find the values of x in each case.
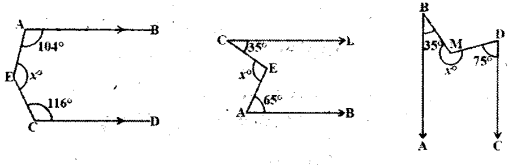
Solution
In each case draw a line ‘l’ parallel to AB and CD through F.
fig (i)
a + 104° = 180° ⇒ a = 180° - 104° = 76°
b+ 116° = 180° ⇒ -b = 180°- 116° = 64°
[∠ interior angles on the same side]
∴ a + b = x = 76° + 64° = 140°
fig-(ii)
a = 35°, b = 65° [∠ alt. int. angles]
x = a + b = 35° + 65° = 100°
fig- (iii)
a + 35° = 180° ⇒ a = 145°
b + 75° = 180° ⇒ b = 105°
[ ∵ interior angles on the same side]
∴ x = a + b = 145° + 105° = 250°
Question 1.
In the given triangles, find out ∠x, ∠y and ∠z
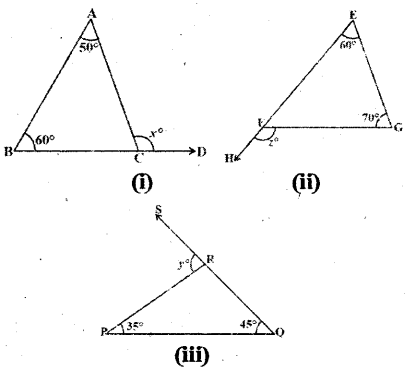
Solution:
In fig(i)
x° = 50° + 60°
(∠ exterior angle is equal to sum of the opposite interior angles)
∴ x= 110°
In fig (ii)
z° = 60° + 70°
(∵ exterior angle is equal to sum of the opposite interior angles)
∴ z = 130°
In fig (iii)
y° = 35° + 45° = 80°
(∵ exterior angle is equal to sum of the opposite interior angles)
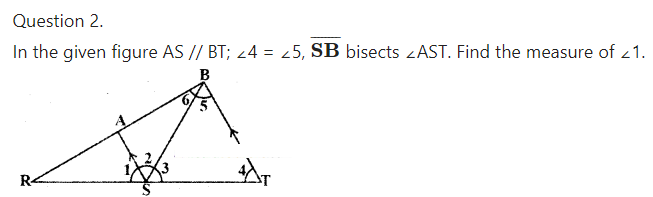
Solution:
Given AS // BT
∠4 = ∠5 and SB bisects ∠AST.
∴ By problem
∠2 = ∠3 ......(1)
For the lines AS // BT
∠2 = ∠5 ( ∵alternate interior angles)
∴ In ΔBST
∠3 = ∠5 = ∠4
Hence ΔBST is equilateral triangle and each of its angle is equal to 60°.
∴∠3 = ∠2 = 60° [by eq. (1)]
Now ∠1 + ∠2 + ∠3 = 180°
∠1 + 60° + 60° = 180°
[ ∵ angles at a point on a line]
∴∠1 = 180° - 120° = 60°
Question 3.
In the given figure AB // CD; BC // DE then find the values of x and y.
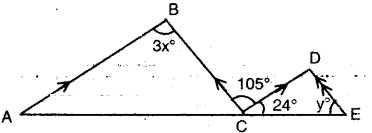
Solution:
Given that AB // CD and BC // DE.
∴ 3x = 105° (∵ alternate interior angles for AB // CD)
x = 105°/3= 35°
Also BC // DE
∴∠D = 105°
(∵ alternate interior angles)
Now in ΔCDE
24° + 105° + y = 180°
(∵ angle sum property)
∴ y = 180° - 129° = 51°
Question 4.
In the given figure BE ⊥ DA and CD ⊥ DA then prove that m∠1 = m∠3.
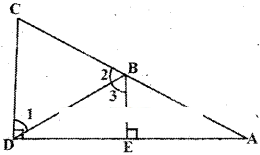
Solution:
Given that CD ⊥ DA and BE ⊥ DA.
⇒ Two lines CD and BE are perpendicular to the same line DA.
⇒ CD // BE (or)
∠D =∠E ⇒ CD // BE
(∵ corresponding angles for CD and BE and DA are transversal)
Now m∠1 = m∠3
(∵alternate interior angles for the lines CD // BE ; DB are transversal)
Hence proved.
Question 5.
Find the values of x, y for which lines AD and BC become parallel.
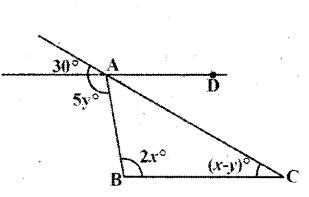
Solution:
For the lines AD and BC to be parallel x - y = 30° (corresponding angles) ... (1)
2x = 5y .....(2)
(∵ alternate interior angles)
Solving (1) & (2)
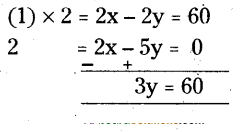
y = 60/3= 20°
Substituting y = 20° in eq. (1)
x - 20° = 30°
⇒ x = 50°
∴ x = 50° and y = 20°
Question 6.
Find the values of x and y in the figure.
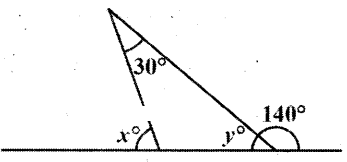
Solution:
From the figure y + 140° = 180°
(∵ linear pair of angles)
∴ y = 180° - 140° = 40°
And x° = 30° + y°
(∵ exterior angle = sum of the opposite interior angles)
x° = 30° + 40° = 70°
Question 7.
In the given figure segments shown by arrow heads are parallel. Find the values of x and y.
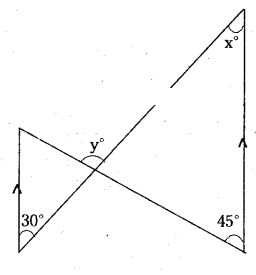
Solution:
From the figure
x° = 30° (∵ alternate interior angles)
y° = 45° + x° (∵ exterior angles of a triangle = sum of opp. interior angles)
y = 45° + 30° - 75°
Question 8.
In the given figure sides QP and RQ of ∠PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°, find ∠PRQ.
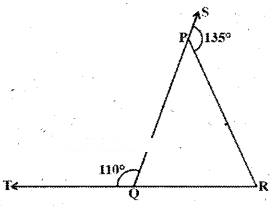
Solution:
Given that ∠SPR = 135° and ∠PQT =110°
From the figure
∠SPR + ∠RPQ = 180°
∠PQT + ∠PQR = 180°
[∵ linear pair of angles]
⇒ ∠RPQ = 180° - ∠SPR
= 180° - 135° = 45°
⇒ ∠PQR = 180° - ∠PQT
= 180°-110° = 70°
Now in APQR
∠RPQ + ∠PQR + ∠PRQ = 180°
[∵ angle sum property]
∴ 45° + 70° + ∠PRQ = 180°
∴ ∠PRQ = 180°-115° = 65°
Question 9.
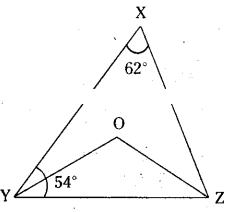
In the given figure ∠X = 62° ; ∠XYZ = 54°. In ?XYZ. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respec-tively find ∠OZY and ∠YOZ.
Solution:
Given that ∠X = 62° and ∠Y = 54°
YO arid ZO are bisectors of ∠Y and ∠Z.
In ΔXYZ
∠X + ∠XYZ + ∠XZY = 180° .
62° + 54° + ∠XZY = 180°
⇒ ∠XZY = 180°- 116° = 64°
Also in Δ𝜏OYZ
∠OYZ = 1/2 ∠XYZ = 1/2 x 54° = 27°
(∵ YO is bisector of ∠XYZ)
∠OZY = 1/2 ∠XZY = 1/2 x 64° = 32
(∵ OZ is bisector of ∠XYZ)
And ∠OYZ + ∠OZY + ∠YOZ = 180°
(∵ angle sum property, ΔOYZ)
⇒ 27 + 32° + ∠YOZ = 180°
⇒ ∠YOZ = 180° - 59° = 121°
Question 10.
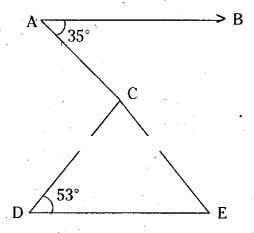
In the given figure if AB // DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.
Solution:
Given that AB // DE, ∠CDE = 53°;
∠BAC = 35°
Now ∠E = 35°
( ∵ alternate interior angles)
Now in ΔCDE
∠C + ∠D + ∠E = 180°
(∵angle sum property, ACDE)
∴∠DCE + 53° + 35° = 180°
⇒ ∠DCE = 180° - 88° = 92°
Question 11.
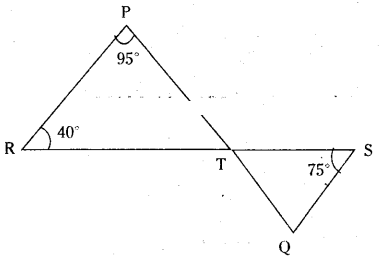
In the given figure if line segments PQ and RS intersect at point T, such that∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.
Solution:
Given that ∠PRT = 40°; ∠RPT = 95°;
∠TSQ = 75°
In ΔPRT ∠P + ∠R + ∠PTR = 180°
(∵angle sum property)
95° + 40° + ∠PTR = 180°
⇒ ∠PTR = 180° - 135° = 45°
Now ∠PTR = ∠STQ
(∵ vertically opposite angles)
In ΔSTQ ∠S + ∠Q + ∠STQ = 180°
(∵ angle sum property)
75° + ∠SQT + 45° = 180°
∴ ∠SQT = 180° - 120° = 60°
Question 12.
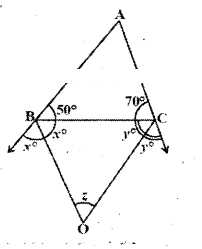
In the given figure, ABC is a triangle in which ∠B = 50° and ∠C = 70°. Sides AB and AC are produced. If ∠ is the measure of angle between the bisec¬tors of the exterior angles so formed, then find ‘z’.
Solution:
Given that ∠B = 50°; ∠C = 70°
Angle between bisectors of exterior angles B and C is ∠.
From the figure
50° + 2x = 180°
70° + 2y = 180°
(∵ linear pair of angles)
∴ 2x= 180°-50°
2x= 130°
x = 130/2
= 65°
2y= 180°-70°
2y= 110°
x = 110°/2
= 55°
Now in ΔBOC
x + y + ∠ = 180° (∵ angle sum property)
65° + 55° + ∠ = 180°
z = 180° -120° = 60°
Question 13.
In the given figure if PQ ⊥ PS; PQ // SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.
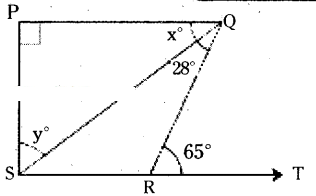
Solution:
Given that PQ ⊥ PS ; PQ // SR
∠SQR = 28°, ∠QRT = 65°
From the figure
∠QSR = x° (∵ alt. int. angles for the lines PQ // SR)
Also 65° = x + 28° (∵ ext. angles = sum of the opp. interior angles)
∴ x° = 65° - 28° = 37°
And x° + y° = 90°
[ ∵ PQ ⊥ PS and PQ // SR. ⇒ ∠P = ∠S]
37° + y = 90°
∴ y = 90° - 37° = 53°
Question 14.
In the given figure ΔABC side AC has been produced to D. ∠BCD = 125° and ∠A: ∠B = 2:3, find the measure of ∠A and ∠B
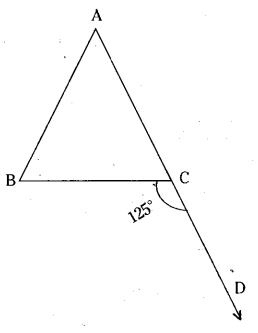
Solution:
Given that ∠BCD = 125°
∠A : ∠B = 2 : 3
Sum of the terms of the ratio
∠A : ∠B = 2 + 3 = 5
We know that ∠A + ∠B = ∠BCD
(∵ exterior angles of triangle is equal to sum of its opp. interior angles)
∴ ∠A = 2/5 x 125° = 50°
∠B = 3/5 x 125° = 75°
Question 15.
In the given figure, it is given that, BC // DE, ∠BAC = 35° and ∠BCE = 102°. Find the measure of 0 ∠BCA i0 ∠ADE and iii) ∠CED.
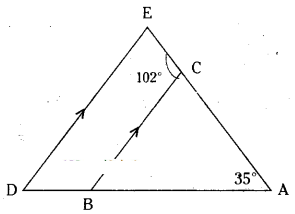
Solution:
Given that BC // DE ; ∠BAC = 35°;
∠BCE = 102°
i) From the figure
102° + ∠BCA = 180°
(∵ linear pair of angles)
∴ ∠BCA = 180° - 102° = 78°
ii) ∠ADE + ∠CBD = 180°
(∵ interior angles on the same side of the transversal)
∠ADE + (78° + 35°) = 180°
(∵ ∠CBD = ∠BAC + ∠BCA)
∴ ∠ADE = 180° - 113° = 67°
iii) From the figure .
∠CED = ∠BCA = 78°
(∵ corresponding angles)
Question 16.
In the given figure, it is given that AB = AC; ∠BAC = 36°; ∠ADB = 45° and ∠AEC = 40°. Find i) ∠ABC
ii) ∠ACB iii) ∠DAB iv) ∠EAC.
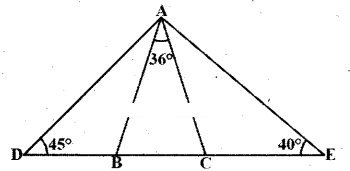

iii) From the figure
∠ABD + ∠ABC = 180°
∠ABD = 180° - 72° = 1086
In ΔABD
∠DAB + ∠ABD + ∠D = 180°
∠DAB + 108° + 45° = 180°
∠DAB = 180° - 153° = 27°
iv) In ΔADE
∠D + ∠A + ∠E = 180°
45° + ∠A + 40° = 180°
⇒ ∠A = 180° -85° = 95°
But ∠A = ∠DAB + 36° + ∠EAC
95° = 27°, + 36° + ∠EAC
∴ ∠EAC = 95° - 63° = 32°
Question 17.
Using information given in the figure, calculate the values of x and y.

Solution:
From the figure In ΔACB
34° + 62° + ∠ACB = 180°
(∵ angle sum property)
∴ ∠ACB = 180° - 96° = 84° .
And x + ∠ACB = 180°
(∵ linear pair of angles) .
∴ x + 84° = 180°
x = 180°-84° = 96°
(OR)
x = 34° + 62° = 96°
( ∵ x is exterior angle, ΔABC)
y = 24° + x°
= 24° + 96° = 120°
(∵ y is exterior angle, ΔDCE)