Question 1.
State whether the following sentences are always true, always false or ambiguous. Justify your answer.
i) There are 27 days in a month.
Solution:
Always false. Generally 30 days or 31 days make a month except February.
ii) Makarasankranthi fells on a Friday.
Solution:
Ambiguous. Makarasankranthi may fall on any day of the week.
iii) The temperature in Hyderabad is 2°C.
Solution:
Ambiguous. Sometimes the temperature may go down to 2°C in winter.
iv) The earth is the only planet where life exist.
Solution:
We can’t say always true. To the known fact, so far we can say this.
v) Dogs can fly.
Solution:
Always false,’as dogs can never fly.
vi) February has only 28 days.
Solution:
Ambiguous. A leap year has 29 days for February.
Question 2.
State whether the following statements are true or false. Give reasons for your answers.
i) The sum of the interior angles of a quadrilateral is 350°.
Solution:
False. Sum of the interior angles of a quadrilateral is 360°.
ii) For any real number x, x2> 0
Solution:
True. This is true for all real numbers,
iii) A rhombus is a parallelogram.
Solution:
True. In a rhombus, both pairs of opposite sides are parallel and hence every rhombus is a parallelogram.
iv) The spm of two even numbers is even.
Solution:
True. This is true for any two even numbers.
v) Square numbers can be written as the sum of two odd numbers.
Solution:
Ambiguous. Since square of an odd number can’t be written as sum of two odd numbers.
Question 3.
Restate the following statements with appropriate conditions, so that they become true statements.
i) All numbers can be represented in prime factorization.
Solution:
Any natural number greater than 1 can be represented in prime factorization.
ii) Two times a real number is always even.
Solution:
Two times a natural number is always even.
iii) For any x, 3x + 1 > 4.
Solution:
For any x > 1; 3x + 1 > 4.
iv) For any x, x3≥ 0.
Solution:
For any x ≥ 0; x3≥ 0.
v) In every triangle, a median is also an angle bisector.
Solution:
In an equilateral triangle, a median is also an angle bisector.
Question 4.
Disprove, by finding a suitable counter example, the statement
x2> y2for all x > y.
Solution:
If x = -8 and y = -10
Here x > y
x2 = (- 8)2= 64 and y2= (- 10)2= 100
But x2> y2is false here. [ ∵ 64 < 100]
(This can be proved for any set of nega-tive numbers or a negative number and a positive number)
Question 1.
Use deductive reasoning to answer the following.
i) Human beings are mortal. Jeevan is a human being. Based on these two statements, what can’ you conclude about Jeevan?
Solution:
From the above statements we can deduce that Jeevan is mortal as it is given that all humans are mortal and Jeevan is a human.
ii) All Telugu people are Indians. X is an Indian. Can you conclude that X belongs to Telugu people?
Solution:
No. X may belong to any other language like Tamil, Kannada, Malayali…. etc.
iii) Martians have red tongues. Gulag is a Martian. Based on these two statements, what can you conclude about Gulag?
Solution:
Gulag had red, tongue.
iv) What is the fallacy in the Raju’s reasoning in the cartoon below

Solution:
All smarts need not be a President. There could be some other persons who are smart too.
Question 2.
Once again you are given four cards. Each card has a number printed on one side and a letter on the other side. Which are the only two cards you need to turn .over to check whether the following rule holds ?
“If a card has a consonant on one side, then it has an odd number on the other side”.

Solution:
You need to turn over B and 8 only. If B has an even number then the rule has broken. Similarly if 8 has a consonant on the other side then also the rule has been broken.
Question 3.
Think of this puzzle. What do you need to find a chosen number from this square ? Four of the clues below are true but do nothing to help in finding the number. Four of the clues are necessary for finding it.
Here are eight clues to use:
- a) The number is greater than 9.
- b) The number is not a multiple of 10.
- c) The number is a multiple of 7.
- d) The number is odd.
- e) The number is not a multiple of 11.
- f) The number is less than 200.
- g) Its ones digit is larger than its tens digit.
- h) Its tens digit is odd.
What is the number ?

Solution:
| Hint |
Conclusion |
| a |
The number may be from 10 to 99
(2nd clue implies, first clue is of no use) No use |
| b |
The number is not any of (10, 20, 30, …………90) |
| c |
The number may be any of (7, 14, 21,28, 35,42, …98) |
| d |
The number may be any of (7,21,35,49, 63, 77,91) |
| e |
The number may be any of (7, 21, 35, 49. 63. 91) |
| f |
No use |
| g |
The numbr may be 35, 49 |
| h |
35 |
Question 1.
Take any three consecutive odd numbers and find their product, for example 1 × 3 × 5 = 15;
3 × 5 × 7 = 105: 5 × 7 × 9 = ……………
ii) Take any three consecutive even numbers and add them, say,
2 + 4 + 6 = 12; 4 + 6 + 8 = 18:
6 + 8 + 10 = 24; 8 + 10 + 12 = 30 ….
so on. Is there any pattern you can guess in these sums ? What can von conjecture about them ?
Solution:
i) 1 × 3 × 5 = 15
3 × 5× 7 = 105
5 × 7 × 9 = 315
7 × 9 × 11 = 693
- The product of any three consecutive odd numbers is odd.
- The product of any three consecutive odd numbers is divisible by ’3′.
- 2 + 4 + 6 = 12; 4 + 6 + 8= 18;
6 + 8 + 10 = 24; 8 + 10 + 12 = 30
- The sum of any three consecutive even numbers is even.
- The sum of any three consecutive even numbers is divisible by 6
- The sum of any three consecutive even numbers is a multiple of 6.
Question 2.
Go back to Pascal’s triangle.
Line-1: 1=11°
Line-2: 11 = 111
Line-3 : 121 = 112
Make a conjecture about line - 4 and line - 5.

Does your conjecture hold ? Does your conjecture hold for line - 6 too ?
Solution:
Line-4 : 1331 = 113
Line-5 : 14641 = 114
Line - 6 : 115
∴ Line – n = 11n-1
Yes the conjecture holds good for line - 6 too.
Question 3.
Look at the following pattern.
i) 28 = 22× 71;
Total number of factors
(2+ 1)(1 + 1) = 3 × 2 = 6
28 is divisible by 6 factors i.e.,
1, 2, 4, 7, 14, 28.
ii) 30 = 21× 31× 51, Total number of .
factors (1 + 1) (1 + 1) (1 + 1) = 2 × 2 × 2 = 8
30 Is divisible by 8 factors i.e., 1, 2, 3, 5, 6, 10, 15 and 30
Find the pattern.
[Hint : Product of every prime base exponent +1)
Solution:
24 = 23× 31
24 has (3+1) (1 + 1) = 4 × 2 = 8 factors
[1, 2, 3, 4, 6, 8, 12 and 24]
36 = 22× 32
Number of factors = (2 + 1) (2 + 1)
3 × 3 = 9 [ 1, 2, 3. 4, 6, 9, 12, 18 and 36]
If N = ap. bq . cr…….. where N is a natural number.
a. b, c … are primes and p, q, r ……. are positive integers then, the number of factors of N =(p- 1)(q+ 1)(r + 1)
Question 4.
Look at the following pattern :
12= 1
112= 121
1112= 12321;
11112= 1234321
111112= 123454321
Make a conjecture about each of the following
1111112=
11111112=
Check if your conjecture is true.
Solution:
1111112= 12345654321
11111112= 1234567654321
(111………. n-times)2= (123 … (n- 1) n (n - 1) (n - 2) 1)
The conjecture is true.
Question 5.
List five axioms (postulates) used in text book.
Solution:
- Things which are equal to the same things are equal to one another.
- If equals are added to equals, the sums are equal.
- If equals are subtracted from equals, the differences are equal.
- When a pair of parallel lines are in-tersected by a transversal, the pairs of corresponding angles are equal.
- There passes infinitely many lines through a given point.
Question 6.
In a polynomial p(x) = x2 + x + 41 put different values of x and find p(x). Can you conclude after putting different values of x that p(x) is prime for all. Is ‘x’ an element of N ? Put x = 41 in p(x). Now what do you find ?
Solution:
p(x) = x2+ x + 41
p(0) = 02+ 0 + 41 = 41 - is a prime
p(1) = 12+ 1 + 41 = 43 - is a prime
p(2) = 22+ 2 + 41 = 47 - is a prime
p(3) = 32+ 3 + 41 = 53 - is a prime
p(41) = 412+ 41 + 41
= 41(41 + 1 + 1)
= 41 x 43 is not a prime.
∴ p(x) = x2+ x + 41 is not a prime for all x.
∴ The conjecture “p(x) = x2+ x + 41 is a prime” is false.
Question 1.
State which of the following are mathematical statements and which are not ? Give reason.
i) She has blue eyes.
Solution:
This is not a mathematical statement. no mathematics is involved in it.
ii) x + 7 = 18
Solution:
This is not a statement, as its truthness cant be determined.
iii) Today is not Sunday.
Solution:
This is not a statement. This is an am biguous open sentence.
iv) For each counting number x, x + 0 = x.
Solution:
This is a mathematical statement.
v) What tune is it?
Solution:
This is not a riathematical statement.
Question 2.
Find counter examples to disprove the following statements.
i) Every rectangle is a square.
Solution:
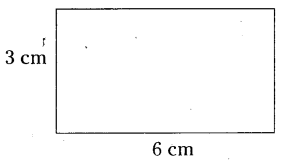
A rectangle and square are equiangular i.e., all the four angles are right angles. This doesn’t mean that they have equal sides.
ii) For any integers x and y,
√x2+y2 = x + y
Solution:
Let x = 3; y = 8
√x2+y2 = √32+82
= √9+64 = √73
x + y = 3 + 8 = 11
Here, √73 ≠ 11
i.e.,√x2+y2≠x+y
iii) If n is a whole number then 2n2+11 is a prime.
Solution:
If n = 11 then 2n2+ 11 = 2 (11)2+ 11
= 11 (2 × 11 + 1) = 11 × (22 + 1)
= 11 × 23 is not a prime.
iv) Two triangles are congruent if all their corresponding angles are equal.
Solution:
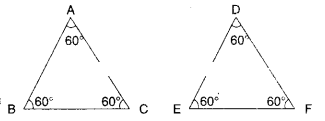
If the corresponding angles are equal then the triangles are only similar.
v) A quadrilateral with all sides are equal is a square.
Solution:
A rhombus is not a square, but all its sides are equal.
Question 3.
Prove that the sum of two odd numbers is even.
Solution:
| Steps |
Reasons |
| 1) (2m + 1); (2n + 1) be the two odd numbers |
General form of an odd number. |
2) (2m + 1) + (2n + 1) = (2m + 2n + 2)
= 2 (m + n + 1) = 2K
Hence proved. |
Adding the two numbers
General form of an even number. |
Question 4.
Prove that the product of two even numbers is an even number.
Solution:
| Steps |
Reasons |
| 1) Let 2m and 2n be two even numbers. |
General form of an even number. |
| 2) 2m.2n = 4mn = 2(2mn) = 2K |
Taking the product Rearranging the numbers. |
| 3) 2K where K = 2mn |
K=2mn |
4) Even number
Hence proved. |
General form of an even number. |
Question 5.
Prove that if x is odd, then x2is also odd.
Solution:
Let x be an odd number.
Then x = 2m + 1
(general form of ah odd number) Squaring on both sides,
x2= (2m + 1)2
= 4m2+ 4m +1
= 2 (2m2+ 2m) + 1
= 2K + 1 where K = 2m2+ 2
Hence x2is also odd.
Question 6.
Examine why they work ?
Choose a number. Double it. Add nine. Add your original number. Divide by three. Add four. Subtract your original number. Your result is seven.
Solution:
Choose a number = x say
Double it = 2x
Add nine = 2x + 9
Add your original number
= 2x + 9 + x = 3x + 9
Divide by 3 = (3x + 9) ÷ 3
=3x/3 + 9/3 = x + 3
Add 4 ⇒ x + 3 + 4 = x + 7
Subtract your original number =
x + 7 - x = 7
Your result is 7 - True.
ii) Write down any three digit number (for example, 425). Make a six digit number by repeating these digits in the same order 425425. Your new number is divisible by 7, 11 and 13.
Solution:
Let a three digit number be xyz.
Repeat the digit = xyzxyz
= xyz × (1001)
= xyz × (7 × 11 × 13)
Hence the given conjecture is true.