Question 1.
A die has six faces numbered from 1 to 6. It is rolled and number on the top face is noted. When this is treated as a random trial.
(Random trial: All possible outcomes are known before hand and the exact outcome can’t be predicted, then only the experiment is treated as a random experiment or a trial.)
a) What are the possible outcomes ?
Solution:
The possible outcomes are 1, 2, 3, 4, 5 and 6.
b) Are they equally likely ? Why ?
Solution:
Yes. All the outcomes are equally likely since every event has equal chance of occurrence or no event has priority to occur.
c) Find the probability of a composite number turning up on the top face.
Solution:
Even : Turning up of a composite number
Possible outcomes = 4, 6
No. of possible outcomes = 2
Total outcomes = 1, 2, 3, 4, 5 and 6
Number of total outcomes = 6
Probability = No. of favourable outcomes/Total no. of outcomes
= 2/6 = 1/3
Question 2.
A coin is tossed 100 times and the following outcomes are recorded. Head : 45 times; Tails : 55 times from the experiment.
a) Compute the probability of each outcome.
Solution:
Head = 45 times; Tails = 55 times
Total = 100
P(H),
Probability of getting Head =45/100
P(T),
Probability of getting Tail =55/100
[P= No. of favourable outcomes/Total no. of outcomes ]
b) Find the sum of the probabilities of all outcomes.
Solution:
P(H) + P(T) = 45/100 + 55/100 = 100/100 = 1
Question 3.
A spinner has four colours as shown in the figure. When we spin it once, find
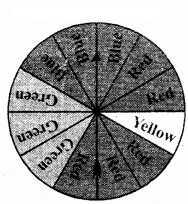
a) At which colour, is the pointer more likely to stop ?
Solution:
Red = 5 sectors; Blue = 3 sectors;
Green = 3 sectors; Yellow = 1 sector
Total = 5 + 3 + 3+1 = 12 sectors
∴ Pointer is more likely to stop at Red.
b) At which colour, is the pointer less likely to stop ?
Solution:
Yellow; as only one sector is shaded in Yellow.
c) At which colours, is the pointer equally likely to stop ?
Solution:
Blue and Green have equal chances; as they are shaded in equal number of sectors.
d) What is the chance the pointer will stop on white ?
Solution:
No chance. Since no sector is shaded in white.
e) Is there any colour at which the pointer certainly stops ?
Solution:
No; as the experiment is a random ex-periment.
Question 4.
A bag contains five green marbles, three blue marbles, two red marbles and two yellow marbles. One marble is drawn out randomly. M)
a) Are the four different colour outcomes equally likely ? Explain.
Solution:
No. As they are not in equal number, they have different chances of occurrence.
b) Find the probability of drawing each colour marble, i.e., P (green), P (blue), P(red) and P (yellow).
Solution:

c) Find the sum of their probabilities.
Solution:
P(Green) + P(Blue) + P(Red) +P(Yellow)
=5/12+3/12+2/12+2/12
=5+3+2+2/12=12/12= 1
Question 5.
A letter is chosen from English alphabet. Find the probability of the letters being
- a) A vowel
- b) A letter comes after P
- c) A vowel or a consonant
- d) Not a vowel
Solution:
Total letters ;= 26 [A, B, C ….. Z]
Probability =No. of favourables/Total no. of outcomes
a) Vowels = a, e, i, o, u [5]
∴ (vowels) =5/26
b) Letter after P = 10
[Q, R, S, T, U, V, W, X, Y, Z]
Probability of a letter that comes after
’P’ =10/26=5/13
c) A vowel or a consonant
Vowel or consonants = 26
[all letters from A to Z]
P(vowel or consonant) =26/26= 1
d) Not a vowel = 21
[other than A, E, I, O, U]
∴ P(not a vowel) =21/26
Question 6.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour (in kg): 4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98,5.04,5.07,5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Total number of bags = 11
No. of bags with a weight more than 5 kg = 7
[5.05, 5.08, 5.03, 5.06, 5.08, 5.04, 5.07]
∴ Probability =favourable outcomes/total outcomes
P(E) =7/11
Question 7.
An insurance company selected 2000 drivers at random (i.e., without any preference of one driver over another) in a particular city to find a relationship between age and accidents. The data obtained is given in the following table.

Find the probabilities of the following events for a driver chosen at random from the city:
i) The driver being in the age group 18-29 years and having exactly 3 accidents in one year.
Solution:
Total number of accidents = (440 + 160 + 110 + 61 + 35 + 505 + 125 + 60 + 22 + 18 +
360 + 45 + 35 + 15 + 9) = 2000
Event: The driver being in the age group (18 - 29) years and having exactly 3 accidents
= 61
P(E) =No. of favourables/Total outcomes=61/2000
ii) The driver being in the age group of 30 - 50 years and having one or more accidents in a year.
Solution:
Favourable outcomes = 125 + 60 + 22 + 18 = 225
Total outcomes = 2000
P(E) =225/2000=9/80
iii) Having no accidents in the year.
Solution:
Favourable outcomes = 440 + 505 + 360 = 1305
Total outcomes = 2000
P(E) =1305/2000=261/400
Question 8.
What is the probability that a randomly thrown dart hits the square board in shaded region ( Take π =22/7 and express in percentage )
Solution:
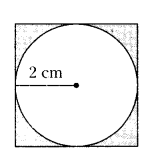
Radius of the circle r = 2 cm
Area of the circle A = πr2=22/7 × 2 × 2 =88/7cm2
Side of the square = 2 × radius
= 2 × 2 = 4cm
Area of the square = S2= 4 × 4 = 16 cm2
Area of the shaded region = Area of the square - Area of the circle
