Question 1.
In ΔABC, ∠ABC = 90°; AD = DC; AB =12 cm, BC = 6.5 cm. Find the area of ΔADB
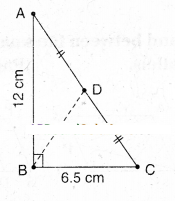
Solution:
ΔADB =1/2 ΔABC [ ∵ AD is a median of ΔABC]
1/2 = [1/2 AB x BC]
=1/4 x 12 x 6.5
= 19.5 cm2
Question 2.
Find the area of a quadrilateral PQRS in which ∠QPS = ∠SQR = 90°, PQ = 12 cm, PS = 9 cm, QR = 8 cm and SR =17 cm.
[Hint: PQRS has two parts]
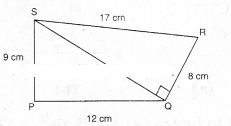
Solution:
Area of ΔQPS = 1/2 x base x height
=1/2 x 9 x 12
= 54cm2
In ΔQPS
QS2= PQ2+ PS2
QS =√122+92=√144+81
=√225=15
Area of ΔQSR =12x base x height
=12x 15 x 8 = 60 cm2
∴ □PQRS = ΔQPS + ΔQSR
= 54 + 60= 114 cm2
Question 3.
Find the area of trapezium ABCD as given in the figure in which ADCE is a rectangle.
[Hint: ABCD has two parts]
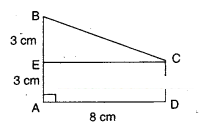
Solution:
Area of trapezium 1
=1/2 (sum of parallel sides) x (distance between the parallel sides)
=1/2 (a + b) h
From the figure, a = 3 + 3 = 6 cm
b = 3 cm
(∵ Opp. sides of rectangle)
h = 8 cm
∴ A =1/2(6 + 3)x8 = 36cm2
Question 4.
ABCD is a parallelogram. The diago-nals AC and BD intersect each other at O. Prove that ar (ΔAOD) = ar (ΔBOQ. [Hint: Congruent figures have equal area]
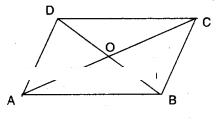
Solution:
Given that □ABCD is a parallelogram.
Diagonals AC and BD meet at ‘O’.
In ΔAOD and ΔBOC
AD = BC [ ∵ Opp. sides of a ||gm]
AO = OC [ ∵ diagonals bisect each
OD = OB other]
ΔAOD = ΔBOC [S.S.S. congruence]
∴ ΔAOD = ΔBOC (i.e., have equal area)
Question 1.
The area of parallelogram ABCD is 36cm2. Calculate the height of parallelogram ABEF if AB = 4.2 cm.
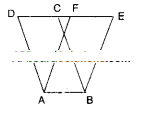
Solution:
Area of □ABCD = 36 cm2
AB = 4.2 cm
then □ABCD = AB X Height
[ ∵ base x height]
36 = 4.2 x h
∴ h =36/4.2
But □ ABCD and □ ABEF are on the same base and between the same parallels.
∴ □ABCD = □ABEF
□ABEF = base x height = AB x height
∴ height =36/4.2= 8.571cm 5
Question 2.
ABCD is a parallelogram. AE is perpendicular on DC and CF is perpendicular on AD. If AB = 10 cm; AE = 8 cm and CF = 12 cm. Find AD.
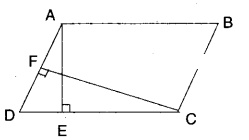
Solution:
Area of parallelogram = base x height
AB x AE = AD x CF
⇒ 10 x 8 = 12 x AD
⇒ AD =10×8/12= 6.666 ……….
∴ AD ≅ 6.7 cm
Question 3.
If E, F, G and H are respectively the midpoints of the sides AB, BC, CD and AD of a parallelogram ABCD, show that ar (EFGH) =1/2 ar (ABCD).
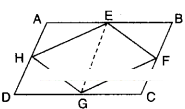
Solution:
Given that □ABCD is a parallelogram.
E, F, G and H are the midpoints of the sides.
Join E, G.
Now
ΔEFG and □EBCG he on the same base EG and between the same parallels
EG // BC.
∴ ΔEFG =1/2□EBCG ……………(1)
Similarly,
ΔEHG =1/2□EGDA …………….(2)
Adding (1) and (2);
ΔEFG + ΔEHG =1/2□EBCG +12□EGDA
□EFGH =1/2[□EBCG +□ EGDA]
□EFGH =1/2[□ABCD]
Hence proved.
Question 4.
What figure do you get, if you join ΔAPM, ΔDPO, ΔOCN and ΔMNB in the example 3 ?
Solution:
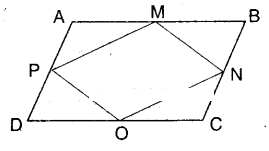
□ABCD is a rhombus.
M, N, O and P are the midpoints of its sides. By joining ΔAPM, ΔDPO, ΔOCN and ΔMNB we get the figure shown by shaded region.
Question 5.
P and Q are any two points lying on the sides DC and AD .respectively of a parallelogram ABCD. Show that ar (ΔAPB) = ar (ΔBQC).
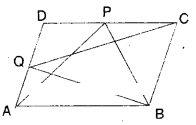
Solution:
ΔAPB and □ABCD are on the same base
AB and between the same parallel lines
AB//CD.
∴ ΔAPB =1/2□ABCD …………… (1)
Also ΔBCQ and □BCDA are on the same base BC and between the same paral¬lel lines BC//AD.
∴ ΔBCQ =1/2□BCDA …………….. (2)
But □ABCD and □BCDA represent same parallelogram.
∴ΔAPB = ΔBCQ [from (1) & (2)]
Question 6.
P is a point in the interior of a parallelogram ABCD. Show that
i) ar (ΔAPB) + ar (ΔPCD) = 1/2 ar(ABCD)
(Hint : Through P, draw a line paral¬lel to AB)
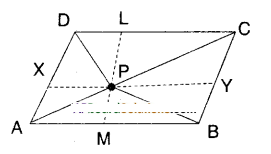
Solution:
□ABCD is a parallelogram.
P is any interior point.
Draw a line¯XYparallel to AB through P.
Now ΔAPB =1/2□AXYB ……………(1)
[∵ ΔAPB, □AXYB lie on the same base AB and beween AB//XY]
Also ΔPCD =1/2□CDXY ………………… (2)
[∵ ΔPCD; □CDXY lie on the same
base CD and between CD//XY]
Adding (1) & (2), we get
Δ APB + ΔPCD =1/2□AXYB +1/2□CDXY
=12[□ AXYB + □ CDXY] [from the fig.)
=12□ABCD
Hence Proved.
(ii) ar (ΔAPD) + ar (ΔPBQ = ar (ΔAPB) + ar (ΔPCD)
Solution:
Draw LM // AD.
ΔAPD + ΔPBC =1/2□AMLD +1/2□BMLC
=1/2[□AMLD +1/2BMLC].
=1/2□ABCD
= ΔAPB +ΔPCD [from(i)]
Hence proved.
[ ∵ ΔAPD, □AMLD are on same base AD and between same parallels AD and LM]
Question 7.
Prove that the area of a trapezium is half the sum of the parallel sides mul¬tiplied by the distance between them.
Solution:
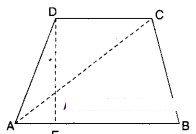
Let □ABCD is a trapezium; AB//CD and
DE ⊥ AB
□ABCD = ΔABC + ΔADC
=1/2 AB x DE +12DC x DE
[∵ Δ =1/2x base x height]
=1/2x DE [AB + DC]
Hence proved.
Question 8.
PQRS and ABRS are parallelograms and X is any point on the side BR.
Show that
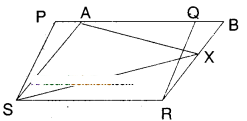
i) ar (PQRS) = ar (ABRS)
Solution:
□PQRS and □ABRS are on the same base SR and between the same parallels SR//PB.
∴ □PQRS = □ABRS
ii) ar (ΔAXS) =1/2 ar (PQRS)
Solution:
From (1) □PQRS = □ABRS
And □ABRS and ΔAXS are on the same base AS and between the same paral¬lels AS//BR.
∴ ΔAXS =1/2□ABRS
=1/2□PQRS from (1)
Hence proved.
Question 9.
A farmer has a held in the form of a parallelogram PQRS as shown in the figure. He took the midpoint A on RS and joined it to points P and Q. In how many parts the field is divided ? What are the shapes of these parts ? The farmer wants to sow groundnuts which are equal to the sum of pulses and paddy. How should he sow ? State reasons.
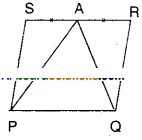
Solution:
From the figure ΔAPQ, □PQRS are on the same base PQ and between the same parallels PQ//SR.
∴ ΔAPQ =12□PQRS
⇒ □PQRS – AAPQ =12□PQRS
∴12□PQRS = ΔASP + ΔARQ
∴ The farmer may sow groundnuts on ΔAPQ region.
The farmer may sow pulses on ΔASP region.
The farmer may sow paddy on ΔARQ region.
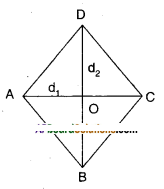
Question 10.
Prove that the area of a rhombus is equal to half of the product of the diagonals.

Question 1.
In a triangle ABC, E is the midpoint of median AD. Show that
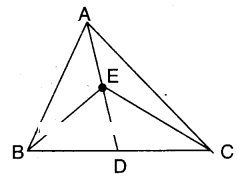
i) ar ΔABE = ar ΔACE
Solution:
In ΔABC; AD is a median.
∴ ΔABD = ΔACD …………….. (1)
(∵ Median divides a triangle in two equal triangles)
Also in ΔABD; BE is a median.
∴ ΔABE = ΔBED =1/2ΔABD …………..(2)
Also in ΔACD; CE is a median.
∴ ΔACE = ΔCDE =1/2ΔACD …………….(3)
From (1), (2) and (3);
ΔABE = ΔACE
(OR)
ΔABD = ΔACD [∵ AD is median in ΔABC]
12ΔABD =1/2ΔACD
[Dividing both sides by 2]
ΔABE = ΔAEC
[∵ BE is median of ΔABD, CE is median of ΔACD]
Hence proved.
ii) arΔABE =1/2 ar(ΔABC)
Solution:
ΔABE =1/2(ΔABD)
[From (i); BE is median of ΔABD]
ΔABE =1/2[1/2ΔABC]
[∵ AD is median of ΔABC]
=1/4ΔABC
Hence,proved.
Question 2.
Show that the diagonals of a paral¬lelogram divide it into four triangles of equal area.
Solution:
□ABCD is a parallelogram.
The diagonals AC and BD bisect each other at ‘O’.
ΔABC and □ABCD lie on the same base AB and between the same parallels AB//CD.
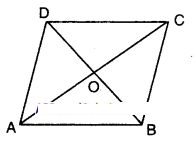
∴ ΔABC =1/4□ABCD
Now in ΔABC; BO is a median
[∵ O is the midpoint of both diagonals AC and BD]
∴ ΔAOB = ΔBOC ………….(1)
[ ∵ Median divides a triangle into two triangles of equal area]
Similarly ∵ABD and □ABCD lie on the same base AB and between the same parallels AB//CD.]
∴ ΔABD =1/2□ ABCD
Also ΔAOB = ΔAOD …………..(2)
[ ∵ AO is the median of AABD]
From (1) & (2)
ΔAOB = ΔBOC = ΔAOD
Similarly we can prove that
ΔAOD = ΔCOD [ ∵ OD is the median of ΔACD]
∴ ΔAOB = ΔBOC = ΔCOD = ΔAOD
Hence proved.
Question 3.
In the figure, ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by ¯AB at O, show that ar (ΔABC) = ar (ΔABD).
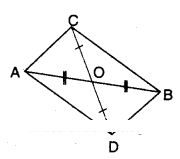
Solution:
From the figure, in ΔAOC; ΔBOD
OA = OB [ ∵ given]
∠AOC = ∠BOD [Vertically opp. angles]
∴ ΔAOC ≅ ΔBOD (SAS congruence)
Thus AC = BD (CPCT)
∠OAC = ∠OBD (CPCT) .
But these are alternate interior angles for the lines AC, BD.
∴ AC // BD
As AC = BD and AC // BD;
□ABCD is a parallelogram.
AB is a diagonal of oABCD
⇒ ΔABC ≅ ΔABD
(∵ diagonal divides a parallelogram into two congruent triangles)
∴ ar(ΔABC) = ar (ΔABD)
Question 4.
In the figure ΔABC; D, E and F are the midpoints of sides BC, CA and AB respectively. Show that
- i)BDEF is a parallelogram
- ii) ar (ΔDEF) =1/4 ar(ΔABC)
- iii) ar (BDEF) =1/2 ar(ΔABC)
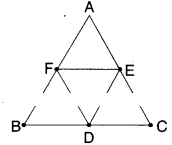
Solution:
i) In ΔABC; D, E and F are the mid¬points of the sides.
∴ EF//BC FD//AC ED//AB
EF =1/2 BC FD =1/2 AC ED =1/2 AB
[ ∵ line joining the mid points of any two sides of a triangle is parallel to third side and equal to half of it]
∴ In □BDEF
BD = EF [ ∵ D is mid point of BC and12BC = EF]
DE = BF
∴ □BDEF is a parallelogram.
ii) □BDEF is a parallelogram (from (i))
Thus ΔBDF = ΔDEF
Similarly □CDFE; □AEDF are also parallelograms.
∴ ΔDEF = ΔCDE =ΔAEF
∴ ΔABC = ΔAEF+ ΔBDF + ΔCDF + ΔDEF
= 4ΔDEF
⇒ ΔDEF =1/4 ΔABC
iii) □BDEF = 2 ΔDEF …………..(1)
(from (ii))
ΔABC = 4 ΔDEF (2)
(from (ii))
From (1) & (2);
ΔABC = 2 (2ΔDEF) = 2 □BDEF
Hence proved.
Question 5.
In the figure D, E are points on the sides AB and AC respectively of ΔABC such that ar (ΔDBC) = ar (ΔEBC). Prove that DE // BC.
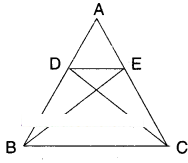
Solution:
ΔDBC = ΔEBC
The two triangles are on the same base BC and between the same pair of lines BC and DE.
As they are equal in area.
∴ BC // DE.
Question 6.
In the figure, XY is a line parallel to BC is drawn through A. If BE // CA and CF // BA are drawn to meet XY at E and F respectively. Show that ar (ΔABE) = ar (ΔACF).
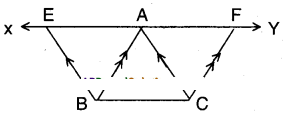
Solution:
Given that XY//BC; BE//CA; CF//BA
In quad ABCF; AB//CF and BC//AF
Hence □ABCF is a parallelogram.
Also in □ACBE ; BC//AE and AC//BE
Hence □ACBE is a parallelogram.
Now in □ABCF and □ACBE
ΔABC = ΔACF …………..(1);
ΔABC = ΔABE …………..(2)
[∵ Diagonal divides a parallelogram into two congruent triangles]
∴ ΔACF = ΔABE [from (1) & (2)]
Hence proved.
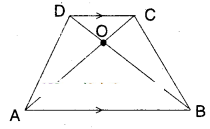
Question 7.
In the figure, diagonals AC and BD of a trapezium ABCD with AB//DC inter¬sect each other at ‘O’. Prove that ar (ΔAOD) = ar (ΔBOC)
Solution:
Given that AB // CD
Now ΔADC and ΔBCD are on the same base and between the same parallels AB // CD.
∴ ΔADC = ΔBCD
⇒ ΔADC – ΔCOD = ΔBCD - ΔCOD
⇒ ΔAOD = ΔBOC [from the figure]
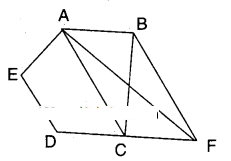
Question 8.
In the figure ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
- (i) ar (ΔACB) = ar (ΔACF)
- (ii) ar (AEDF) = ar (ABCDE)
Solution:
ABCDE is a pentagon.
AC//BF
i) ΔACB and ΔACF are on the same base AC and between the same parallels AC//BF.
∴ ΔACB = ΔACF
ii) □AEDF = □AEDC + ΔACF
= □AEDC + ΔABC
[ ⇒ ΔACF = ΔACB]
= area (ABCDE)
Hence proved.
Question 9.
In the figure, if ar (ΔRAS) = ar (ΔRBS) and ar (ΔQRB) = ar (ΔPAS) then show that both the quadrilaterals PQSR and RSBA are trapeziums.
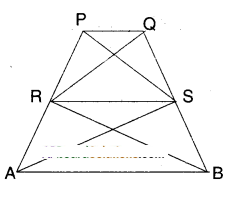
ΔRAS = ΔRBS ………….. (1)
Both the triangles are on the same base RS and between the same pair of lines RS and AB.
As their areas are equal RS must be parallel to AB.
⇒ RS//AB
∴ □ABRS is a quadrilateral in which AB//RS.
∴ □ABRS (or) □RSBA is a trapezium.
Now AQRB = APAS (given)
⇒ ΔQRB – ΔRBS = ΔPAS - ΔRAS
[from (1) ΔRBS = ΔRAS]
⇒ ΔQRS = ΔPRS
These two triangles are on the same base RS and between the same pair of lines RS and PQ.
As these two triangles have same area RS must be parallel to PQ.
⇒ RS // PQ
Now in quad PQRS; PQ//RS.
Hence □PQRS is a trapezium.
Question 10.
A villager Ramayya has a plot of land in the shape of a quadrilateral. The grampanchayat of the village decided to take over some portion of his plot from one of the comers to construct a school. Ramayya agrees to the above proposal with the condition that he should be given equal amount of land in exchange of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will implemented. (Draw a rough sketch of the plot.)
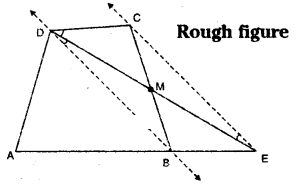
Solution:
Let □ABCD is the plot of Ramayya.
School be constructed in the region ΔMCD where M is a point on BC such that □ABCD ≅ ΔADE
Draw the diagonal BD.
Draw a line parallel to BD through C which meets AB produced at E.
Join D, E
ΔADE is the required triangle.

Analysis:
ΔCED and ΔCEB are on the same base CE and between the same parallels CE and DB.
∴ ΔCED = ΔCEB [also from the figure]
ΔCEM + ΔCMD = ΔCEM + ΔBME
∴ ΔCMD = ΔBME
∴ ΔADE = □ABCD