Question 1.
Find the lateral surface area and total surface area of the following right prisms.
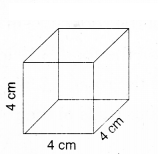
i)L.S.A. = 4l2
= 4 × 42
= 64cm2
T.S.A = 6l2
= 6 × 42= 96cm2
ii) L.S.A. =2h(l + b)
= 2 × 5 (8 + 6)
= 10 × 14 = 140 cm2
T.S.A. = 2 (lb + bh + lh)
= 2(8 × 6 + 6 × 5 + 8 × 5)
= 2 (48 + 30 + 40)
= 236 cm2
Question 2.
The total surface area of a cube is 1350 sq.m. Find its volume.
Solution:
Given T.S.A. of a cube 6l2= 1350
l2 = 1350/6
l2 = 225
∴ l = √225 = 15m
∴ Volume of the cube = l3
= 15 × 15 × 15
= 3375 m3
Question 3.
Find the area of four walls of a room (Assume that there are no doors or windows) if its length 12 m; breadth 10 m and height 7.5 m.
Solution:
Length of the room = 12 m
Breadth of the room = 10 m
Height of the room = 7.5 m
Area of four walls of the room
A = 2h (l + b)
A = 2 × 7.5 (12 + 10)
= 15 × 22
= 330 m2
Question 4.
The volume of a cuboid is 1200 cm3. The length is 15 cm and breadth is 10 cm. Find its height.
Solution:
Length of a cuboid, ‘l’ = 15 cm
Breadth of the cuboid, b = 10 cm
Volume of the cuboid, V = lbh = 1200.cm3
Let the height = h
∴ 15 × 10 × h = 1200
∴ h =1200/15×10
= 8 cm
Question 5.
How does the total surface area of a box change if
i) Each dimension is doubled ?
Solution:
Let the original dimensions be Length - l units
Breadth - b units
Height - h units
Then T.S.A = 2 (lb + bh + lh)
If the dimensions are doubled then
Length = 2l
Breadth = 2b
Height = 2h
T.S.A. = 2 (2l. 2b + 2b . 2h + 2l . 2h)
= 2 (4lb + 4bh + 4lh)
= 4 × [2 (lb + bh + lh]
= 4 × original T.S.A.
i.e., T.S.A. increases by 4 times.
ii) Each dimension is tripled ?
Solution:
Let the original and changed dimensions are l, b, h and 31, 3b, 3h
Original T.S.A. = 2 (lb + bh + lh)
Changed T.S.A
= 2 (3l . 3b + 3b . 3h + 3l. 3h)
Changed T S.A. = 2 (9lb + 9bh + 9lh)
= 9 × [2 (lb + bh + lh)]
= 9 [original T.S.A.]
Thus original T.S.A. increased by 9 times if each dimension is tripled.
Question 6.
The base of a prism is triangular in shape with sides 3 cm, 4 cm and 5 cm. Find the volume of the prism if its height is 10 cm.
Solution:
Volume of triangular prism = Area of the base × height
Sides of the triangle are 3 cm, 4 cm and 5 cm.
Area = s (s - a) (s - b) (s - c)
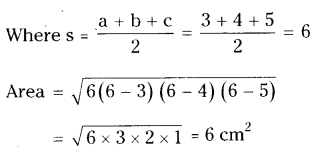
∴ Volume of the prism = 6 × 10 = 60 cm3
(OR)
3 cm, 4 cm and 5 cm are the sides of right triangle.
∴ Area of the triangle
=1/2 bh = 1/2 × 3 × 4 = 6 cm2
Volume of prism = base area × height
= 6 × 10 = 60cm3
Question 7.
A regular square pyramid is 3 m height and the perimeter of its base is16 m Find the volume of the pyramid.
Solution:
Perimeter of the base = 16 m
Height of the pyramid 3 m
Volume of the pyramid
= 1/3 × volume of prism
= 1/3 × (base area x height)
= 1/3 × 4 × 4 × 3= 16m [4 × side=16 ∴ side = 4 m Area = s2= 4 × 4]
Question 8.
An Olympic swimming pool is in the shape of a cuboid of dimensions 50 m long and 25 m wide. If it is 3 m deep throughout, how many litres of water does it hold ?
Solution:
Dimensions of the swimming pool are
Length = 50 m
Breadth = 25 m
Deep = 3 m
∴ Volume of the swimming pool
V = lbh
V = 50 × 25 × 3 = 3750 m3
∴ It can hold 37,50,000 litres of water.
[∵ 1 m3 = 1000 lit.]
Question 1.
A closed cylindrical tank of height 1.4 m and radius of the base is 56 cm is made up of a thick metal sheet. How much metal sheet is required ?
(Express in square metres).
Solution:
Radius of the tank r’ = 56 cm
=56/100 m = 0.56m
Height of the tank h = 1.4 m
T.S.A. of a cylinder = 2πr (r + h)
∴ Area of the metal sheet required = 2πr (r + h)
A = 2 × 22/7 × 0.56 × (0.56 + 1.4)
= 2 × 22 × 0.08 × 1.96
= 6.8992 m2
= 6.90 m2
Question 2.
The volume of a cylinder is 308 cm3 . Its height is 8 cm. Find its lateral surface area and total surface area.
Solution:
Volume of the cylinder V = πr2h
= 308 cm3
Height of the cylinder h = 8 cm
∴ 308 = 22/7 . r2 x 8
r2= 308 × 7/22 x 1/8
r2= 12.25
∴ r =√12.25 = 3.5cm
L.S.A. = 2πrh
= 2 × 22/7× 3.5 × 8 = 176cm2
T.S.A. = 2πr (r + h)
2 × 22/7 × 3.5 (3.5 + 8)
= 2 × 22 × 0.5 × 11.5 = 253 cm2
Question 3.
A metal cuboid of dimensions 22 cm × 15 cm × 7.5 cm was melted and cast into a cylinder of height 14 cm. What is its radius ?
Solution:
Dimensions of the metal cuboid
= 22 cm × 15 cm × 7.5 cm
Height of the cylinder, h = 14 cm
Cuboid made as cylinder
∴ Volume of cuboid = Volume of cylinder
lbh = 2πr2h
⇒ 22 × 15 × 7.5 = 22/7 × r2× 14
⇒ r2=22×15×7.5×7/14×22
⇒ r2= 7.5 × 7.5
r = 7.5 cm
Question 4.
An overhead water tanker is in the shape of a cylinder has capacity of 616 litres. The diameter of the tank is 5.6 m. Find the height of the tank.
cagp)
Solution:
Volume of the cylinder, V = πr2h = 616
Diameter of the tank = 5.6 m
Thus its radius, r = d/2 = 5.6/2 = 2.8 m
Height = h (say)
∴ πr2 h = 616
22/7 × 2.8 × 2.8 × h = 616
h = 616×7/22×2.8×2.8 = 25
∴ Height = 25 m
Question 5.
A metal pipe is 77 cm long. The inner diametre of a cross section is 4 cm; the outer diameter being 4.4 cm (see figure). Find its
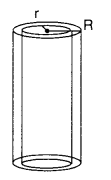
i) Inner curved surface area
ii) Outer curved surface area
iii) Total surface area
i) Inner curved surface area
Solution:
Height of the pipe = 77 cm
Inner diameter = 4 cm
Inner radius = d/2 = 4/2 = 2 cm
∴ Inner C.S.A. = 2πrh
= 2 × 22/7 × 2 × 77
= 88 × 11 = 968cm2
ii) Outer curved surface area
Solution:
Outer diameter = 4.4 cm
∴ Outer radius, r = d/2 = 4.4/2 = 2.2 cm
Height of the pipe, h = 77 cm
∴ Outer C.S.A. = 2πrh
= 2 × 22/7 × 2.2 × 77
= 96.8 × 11
= 1064.8 cm2
iii) Total surface area Sol. Total surface area .
= Inner C.S.A + Outer C.S.A
= 968 + 1064.8
= 2032.8 cm2
Question 6.
A cylindrical pillar has a diameter of 56 cm and is of 35 m high. There are 16 pillars around the building. Find the cost of painting the curved surface area of all the pillars at the rate of ? 5.50 per 1 m2.
Solution:
Diametre of the cylindrical pillar = 56 cm
Thus its radius, r = d/2
=56/2 = 28cm = 28/100 m = 0.28m
Height of the pillar, h = 35 m
Total number of pillars =16
Cost of painting = ₹ 5.50 per sq. m.
C.S.A. of each pillar = 2πrh
= 2 × 22/7 × 0.28 × 35
= 2 × 22 × 0.04 × 35 = 61.6 m2
∴ C.S.A. of 16 pillars = 16 × 61.6 = 985.6 m2
Cost of painting 16 pillars at the rate of ₹ 5.5 per sq.m. = 985.6 × 5.5
= ₹ 5420.8
Question 7.
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to roll once over the play ground to level. Find the area of the play ground in m2
Soi. Diameter of the roller = 84 cm
Thus radius = 84/2 = 42 cm
= 42/100 m = 0.42m
Length of the roller =120 cm
= 120/100 = 1.2m
It takes 500 complete revolutions to roll over the play ground.
Thus 500 × L.S.A. of the roller
= Area of the play ground
∴ Area of the play ground = 500 × 2πrh
= 500 × 2 × 22/7 × 0.42 × 1.2 = 1584 m2
Question 8.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find (i) its inner curved surface area (ii) the cost of plastering this curved surface at the rate of Rs. 40 per m2.
Solution:
Inner diameter of the circular well, d = 3.5 m
Thus its radius, r = d/2 = 3.52 = 1. 75 m
Depth of the well (height) = 10 m
i) Inner C.S.A. = 2πrh
= 2 × 227 × 1.75 × 10
= 110 m2
ii) Cost of plastering at the rate of
₹ 40 / m2 = 110 × 40 = ₹ 4400
Question 9.
Find (i) the total surface area of a closed cylindrical petrol storage tank whose diameter 4.2 m and height 4.5 m.
Solution:
Diameter of the cylindrical tank ‘d’ = 4.2m
Thus its radius, r = d/2 = 4.2/2 = 2.1 m
Height of the tank, h = 4.5 m
T.S.A. of the tank = 2πr (r + h)
= 2 × 22/7 × 2.1 (2.1 + 4.5)
= 2 × 22 × 0.3 × 6.6 = 87.12m2
ii) How much steel sheet was actually used, if 1/12 of the steel was wasted in making the tank ?
Solution:
1/12 of the sheet was wasted.
= > 1 - 1/12 = 11/12of the sheet was used
in making the tank.
Let the metal sheet originally brought was = x m2
11/12 x = 87.12m2
∴ x = 87.12 x 12/11 = 95.04m2
Question 10.
A one side open cylindrical drum has inner radius 28 cm and height 2.1 m. How much water you can store in the drum? Express in litres.
(1 litre = 1000 c.c)
Solution:
Inner radius of the cylindrical drum ‘r’ = 28 cm
. Its height, h = 2.1 m = 2.1 x 100 = 210 cm
Volume of the drum = πr2h
= 22/7 x 28 x 28 x 210
= 22 x 4 x 28 x 210
= 517440 cc
=517440/1000
= 517.44 lit.
Question 11.
The curved surface area of the cylinder is 1760 cm2 and its volume is 12320 cm3. Find its height.
Solution:
C.S.A of the cylinder = 2πrh = 1760 cm2
Volume of the cylinder = πr2h
= 12320 cm3
Height = h (say)
Volume/C.S.A.= πr2h/2πrh= 12320/1760
⇒r/2 = 7
∴ r = 7 x 2 = 14cm
Now 2πrh = 1760cm2
2 x22/7 x 14h = 1760
h =1760x7/2x22x14= 20cm
∴Height of the cylinder = 20cm
Question 1.
The base area of a cone is 38.5 cm Its volume is 77 cm3. Find its height.
Solution:
Base area of the cone, πr2= 38.5 cm2
Volume of the cone, V =1/3πr2h = 77
πr2= 38.5
22/7r2= 38.5
r2= 38.5 x 7/22
r2= 12.25
r =√12.25 = 3.5
V=1/22 x 22/7 x 3.5 x 3.5 x h = 77
∴ h =77x3x7/22x12.25= 6
∴ Height of the cone = 6 cm
Question 2.
The volume of a cone is 462 m3. Its base radius is 7 m. Find its height.
Solution:
The volume of a cone”V’=13πr2h = 462
Radius ‘r’ = 7 m
Height = h (say)
1/3 x 22/7 x 7 x h = 462
h =462x3/22x7= 9
∴ Height = 9m
Question 3.
Curved surface area of a cone is 308 cm2and its slant height is 14 cm. Find (1) radius of the base (ii) total surface area of the cone.
Solution:
C.S.A. of the cone, πrl = 308
Slant height, l = 14 cm
i) πrl = 308; l = 14 cm
22/7 x r x 14 = 308
r =308/44= 7cm
ii) T.S.A. = πrl + πr2
= πr (r + l) =22/7x 7 x (7 + 14)
= 22 x 21 = 462 cm3
Question 4.
The cost of painting the total surface area of a cone at 25 paise per cm2 is ₹176. Find the volume of the cone, if its slant height is 25 cm.
Solution:
Slant height of the cone, l = 25 cm
Total cost at the rate of 25 p/cm2
= ₹176
∴ Total surface area of the cone
= 176/25 x 100 = 176 x 4 = 704cm2
But T.S.A. of the cone = πr (r + l) = 704
Thus 22/7 r(r + 25) = 704
r(r + 25) = 704x7/22 = 224
r2+ 25r = 224
⇒ r2+ 32r - 7r - 224 = 0
⇒ r (r + 32) - 7 (r + 32) = 0
⇒ (r + 32) (r - 7) = 0
⇒ r = 7 (∵ ’r’ can’t be negative)
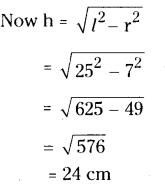
∴ Volume of the cone = 1/3 πr2h
= 1/3 x 22/7 x 7 x 7 24
= 22 x 7 x 8 = 1232cm3
Question 5.
From a circle of radius 15 cm, a sector with angle 216° is cut out and its bounding radii are bent so as to form a cone. Find its volume.
Solution:
Radius of the sector, ‘r’ = 15 cm
Angle of the sector, ‘x’ = 216°
∴ Length of the arc, l = x/360 x 2πr
= 216/360 2πr= 3/5 (2πr)
Perimeter of the base of the cone = Length of the arc
2πr of cone == 6/5 πr of the circle
Radius of the cone ‘r’ =35x 15 = 9
Radius ‘r’ of the circle = slant height l of the cone = 9 cm
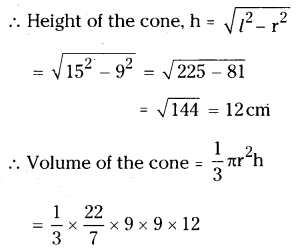
= 1018.3 cm3
Question 6.
The height of a tent is 9 m. Its base diameter is 24 m. What is its slant height ? Find the cost of canvas cloth required if it costs ₹14 per sq.m.
Solution:
Height of a conical tent ‘h’ = 9 m
Base diameter = 24 m
Thus base radius ’r’= d/2 = 24/2 = 12m
Cost of canvas = ₹ 14 per sq.m.
C.S.A. of the cone = πrl

Question 7.
The curved surface area of a cone is 1159 5/7 cm2. Area of its base is 254 4/7 cm2. Find its volume.
Solution:
C.S.A. of the cone = πrl
Question 8.
A tent is cylindrical to a height of 4.8 m and conical above it. The ra¬dius of the base is 4.5 m and total height of the tent is 10.8 m. Find the canvas required for the tent in square
meters.
Solution:
Radius of cylinder, l = 4.5 m
Height of the cylinder = h = 4.8 m
∴ C.S.A. of the cylinder = 2πrh
= 2 x 22/7 x 4.5 x 4.8
= 135.771 m2
Radius of the cone ‘r’ =
Radius of the cylinder = 4.5 m
Height of the cone ’h’ = 10.8 - 4.8 = 6 m
∴ Slant height of the cone
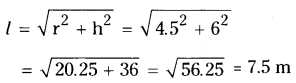
∴ C.S.A. of the cone = πrl
= 227 x 4.5 x 7.5
= 742.57 = 106.071m2
∴ Total canvas required
= C.S.A of cylinder + C.S.A. of cone
= 135.771 + 106.071
= 241.842 m2
Question 9.
What length of tarpaulin 3 m wide will be required to make a conical tent of height 8 m and base radius 6m? Assume that extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (use π = 3.14) [Note : Take 20 cm as 0.6 m2]
Solution:
Radius of the cone, r = 6 m
Height of the cone, h = 8 m
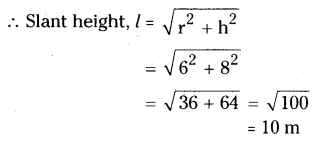
∴ C.S.A. = πrl = 3.14 x 6 x 10 = 188.4 m2
Let the length of the tarpaulin = l
∴ Area of the tarpaulin, lb = 188.4 + 0.6
= 189 m2
⇒ 3l = 189
⇒ l = 189/3 = 63m
Question 10.
A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 27 cm. Find the area of the sheet required to make 10 such caps.
Solution:
Radius of the cone, r = 7 cm
Height of the cone, h = 27 cm
Slant height of the cone (l)
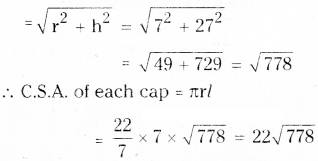
∴ Total area of the sheet required for
10 caps = 10 x 22 √778
= 6136.383 cm2
Question 11.
Water is pouring into a conical vessel (as shown in the given figure), at the rate of 1.8 m3per minute. How long will it take to fill the vessel?
Solution:
From the figure, diameter of the cone 5.2 m
Thus its radius ’r’ = 5.2/2 = 2.6 m
∴ Height of the cone = h = 6.8 m
Volume of the cone = 1/3 πr2h
= 1/3 x 22/7 x 2.6 x 2.6 x 6.8
= 1011.296/21
= 48.156 m3
Quantity of water that flows per minute
= 1.8 m3
∴ Total time required = Total volume/1.8
= 48.156/1.8 = 26.753
27 minutes.
Question 12.
Two similar cones have volumes 12π CU. units and 96π CU. units. If the curved surface area of smaller cone is 15π sq.units, what is the curved surface area of the larger one?
Solution:
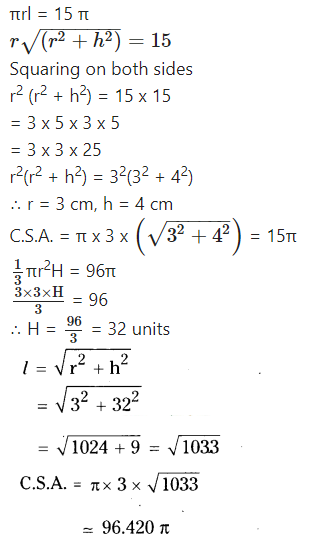
Question 1.
The radius of a sphere is 3.5 cm. Find its surface area and volume.
Solution:
Radius of the sphere, r = 3.5 cm

Question 2.
The surface area of a sphere is 1018 2/7 cm2. What is its volume ?
Solution:
Surface area of sphere = 4πr2
= 1018 2/7 cm2
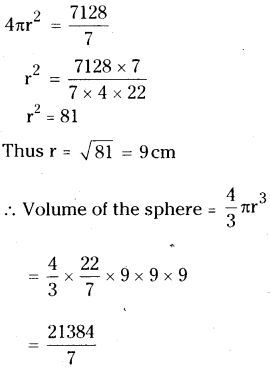
= 3054.857cm3
≅ 3054.86cm3
Question 3.
The length of equator of the globe is 44 cm. Find its surface area.
Solution:
Length of the equator of the globe 2πr = 44 cm.
2 x 22/7 x r = 44
∴ r = 44x7/2x22= 7cm
∴ surface area = 4πr2
= 4 x 22/7 x 7 x 7
= 4 x 22 x 7
= 616cm2
Question 4.
The diameter of a spherical ball is 21 cm. How much leather is required to prepare 5 such balls?
Solution:
Diameter of the spherical ball d’ = 21 cm
Thus, its radius r = d/2 = 21/2 = 10.5 cm
Surface area of one ball = 4πr2
= 4 x 22/7 x 10.5 x 10.5
= 88 x 1.5 x 10.5 = 1386 cm2
∴ Leather required for 5 such balls
= 5 x 1386 = 6930 cm2
Question 5.
The ratio of radii of two spheres is 2 : 3. Find the ratio of their surface areas and volumes.
Solution:
Ratio of radii r1: r2= 2 : 3
Ratio of surface area
= 4πr12: 4πr22
= 22: 32= 4 : 9
Ratio of volumes
= 4/3 πr13: 4/3 πr23
= 23: 33= 8 : 27
Question 6.
Find the total surface area of hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
Radius of the hemisphere = 10 cm
Total surface area of the hemisphere = 3πr2
= 3 x 3.14 x 10 x 10
= 9.42 x 100
= 942 cm2
Question 7.
The diameter of a spherical balloon increases from 14 cm. to 28 cm. as air is being pumped into it. Find the ratio of surface areas of the balloons in the
two cases.
Solution:
The diameter of the balloon, d = 14 cm
Thus, its radius, r = d/2 = 14/2 = 7 cm
∴ Surface area = 4πr2= 4 x 22/7 x 7 x 7
= 88 x 7 = 616cm2
When air is pumped, the diameter = 28 cm
thus its radius = d/2 = 28/2 = 14 cm
Its surface area = 4πr2
= 4 x 22/7 x 14 x 14
= 88 x 28 = 2464 cm2
Ratio of areas = 616 : 2464
= 1 : 4
(OR)
Original radius = 14/2 = 7 cm
Increased radius = 28/2 = 14cm
Ratio of areas = r12: r22
= 72: 142
= 7 x 7 : 14 x 14
= 1:4
Question 8.
A hemispherical bowl is made of brass, 0.25 cm thickness. The inner radius of the bowl is 5 cm. Find the ratio of outer surface area to inner surface area.
Solution:
Inner radius of the hemisphere ‘r’ = 5 cm
Outer radius of the hemisphere ‘R’
= inner radius + thickness
= (5 + 0.25) cm = 5.25 cm
Ratio of areas = 3πR2: 3πr2
= R2: r2
= (5.25)2: 52
= 27.5625 : 25
= 1.1025:1
= 11025 : 10000
= 441 : 400
[Note : If we read “radius as diameter” then we get the T.B. answer]
Question 9.
The diameter of a lead ball is 2.1 cm. The density of the lead used is 11.34 g/c3. What is the, weight of the ball ?
Solution:
The diameter of the ball = 2.1 cm
Thus, its radius, r = d/2 = 2.1/2 = 1.05 cm
Volume of the ball V’ = 4/3 πr3
=4/3 x 22/7 x 1.053=101.87/21
∴Weight of the ball = Volume x density
= 4.851 x 1.34
= 55.010
Question 10.
A metallic cylinder of diameter 5 cm 1 and height 3 1/3 cm is melted and cast into a sphere. What is its diameter ?
Solution:
Diameter of the cylinder’d’ = 5 cm
Thus, its radius, r = d/2 = 5/2 = 2.5 cm
Height of the cylinder,
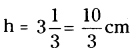
Volume of the cylinder
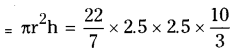
Given that cylinder melted to form sphere
∴ Volume of the sphere = Volume of the cylinder
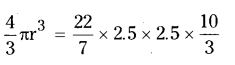
(Where r is the radius of the sphere)
r3 = 3/4 x 2.5 x 2.5 x 10/3
r3 = 2.53
∴ r = 2.5 cm
Hence its diameter, d = 2r
= 2 x 2.5 = 5 cm
Question 11.
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold ?
Solution:
Diameter of the hemispherical bowl = 10.5 cm
Thus its radius = d/2 = 10.5/2 = 5.25cm
Quantity of milk, the bowl can hold = Volume of the bowl = 2/3πr3
= 2/3 x 22/7 x 5.25 x 5.25 x 5.25
= 303.1875 cm3
=303.1875/1000 lit = 0.303 lit.
Question 12.
A hemispherical bowl has diameter 9 cm. The liquid is poured into cylindrical bottles of diameter 3 cm and height 3 cm. If a full bowl of liquid is Riled in the bottles, find how many
bottles are required ?
Solution:
Diameter of the hemispherical bowl ‘d’ = 9 cm
Its radius, r = d/2 = 9/2 = 4.5cm
Volume of its liquid = Volume of the bowl = 2/3 πr3
= 2/3 x 22/7 x 4.5 x 45 x 4.5
Diameter of the cylindrical bottle, d = 3 cm
Its radius, r = d/2
=3.02
= 1.5cm
Height of the bottle, h = 3 cm
Let the number of bottles required = n
Then total volumes of these n bottles = n πr2h
But this is equal to volume of the bowl
Hence n. 22/7 × 1.5 × 1.5 × 3
= 2/3 × 22/7 × 4.5 × 4.5 × 4.5
∴ n = 23×20.25/1.5 = 9
∴ Number of bottles required = 9