Exploring Geometrical Figures

Question 1.
Name five pairs of congruent objects, you use daily.

Solution:
i) Pair of ear rings.
ii) Wheels of a cycle.
iii) Equal lengths of scales.
iv) Pair of bangles.
v) Mathematics textbooks of same class.

Question 2.
(a) Draw two congruent figures. Are they similar? Explain
(b) Take two similar shapes. If you slide rotate or flip one of them, does the similarity remain?

Solution:
a) ΔABC ≅ ΔPQR

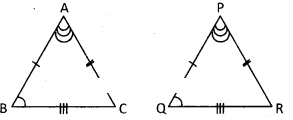
From ΔABC & ΔPQR
AB = PQ
AC = PR
BC = QR
∠A = ∠P
∠B = ∠Q
∠C = ∠R
∴ Congruent triangles are similar to each other.
But similar triangles are not congruent.

b)

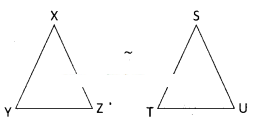
From fig. ΔXYZ and ΔSTU are similar triangles. If these triangles are rotated even they are similar to each other.

Question 3.
If Δ ABC ≅ Δ NMO, name the congruent sides and angles.

Solution:

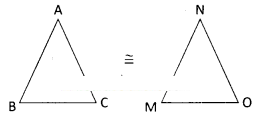
From the congruent triangles
ΔABC ≅ ΔNMO
AB = NM
BC = MO
AC = NO
∠A = ∠N
∠B =∠M
∠C = ∠O

Question 4.
State whether the following statements are true. Explain with reason.

• (i) Two squares of side 3 cm each and one of them rotated through 45° are congruent.
• (ii) Any two right triangles with hypotenuse 5 cm, are congruent.
• (iii) Any two circles of radii 4 cm each are congruent.
• (iv) Two equilateral triangles of side 4 cm each but labeled as A ABC and A LHN arc not congruent.
• (v) Mirror image of a polygon is congruent to the original.

Solution:
i) True. If the square is rotated 45° then it is remaining congruent.
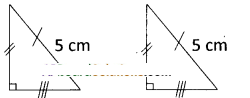
ii) True. If the hypotenuse of two right triangles are equal, then the two triangles are congruent to each other, [∵ Their corresponding sides and angles will also be equal]

(iii) True
Since they are having equal radii (r₁= r₂= 4 cm )
= 4 cm).
∴ The given circles are congruent.

iv) False.
If two sides of one triangle are equal to the corresponding two sides of another triangle, then the third sides are in the proportion.
∴ ΔABC ≅ ΔLHN

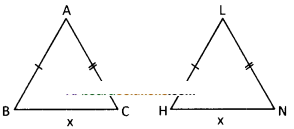
But given tXABC,’LLHN. Then it is false.

v) True.
Always the mirror images of a polygon is congruent to the original.

Question 5.
Draw a polygon on a square dot sheet. Also draw congruent figures in different directions and mirror image of it.

Solution:

Question 6.
Using a square dot sheet or a graph sheet draw a rectangle and construct a similar figure.
Find the perimeter and areas of both and compare their ratios with the ratio of their
corresponding sides.

Solution:

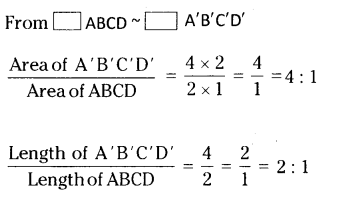
Question 7.
7 pillars are used to hold a slant iron gudder as shown in the figure. If the distance between every two pillars is 1 m and height of the last piller is 10.5 m. Find the height of pillar.

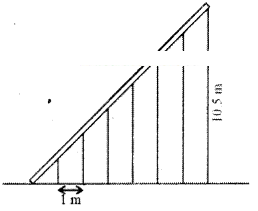
Solution:

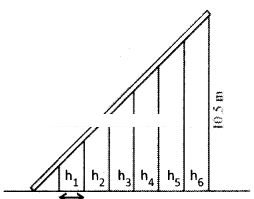
The height of the 1st pillar
h₁=1/7 x 10.5 = 1.5m.

The height of 2nd pillar
h₂=2/7 x 10.5 = 3m.

The height of 3rd pillar
h₃= 3/7 x 10.5 = 4.5 m.

The height of 4th pillar
h₄ = 4/7 x 10.5 = 6 m.

The height of 5th pillar
h₅= 5/7 x 10.5 = 7.5 m.

The height of 6th pillar
h₆=6/7 x 10.5 = 9 m.

Question 8.
Standing at 5 m apart from a vertical pole of height 3 m, Sudha observed a building at the back of the piller that tip of the pillar is in line with the top of the building. If the distance
between pillar and building is 10 m, estimate the height of the building. [Here height of
Sudha is neglected]

Solution:
ΔAOAB ~ ΔOCD

The corresponding sides of similar triangles are in a same proportion^?

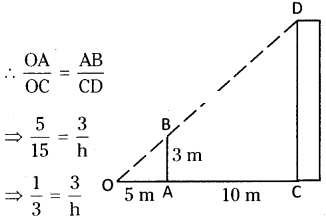
⇒ h = 3 x 3 = 9
∴ h = height of a building = 9 mts.

Question 9.
Draw a quadrilateral of any measurements. Construct a dilation of scale factor 3. Measure their corresponding sides and verify whether they are similar.

Solution:

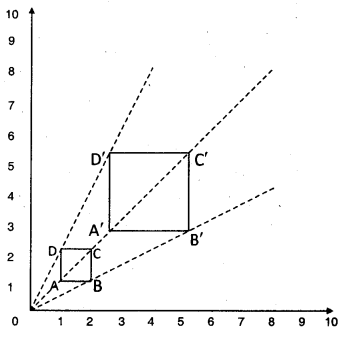
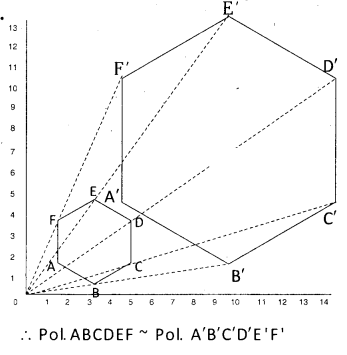
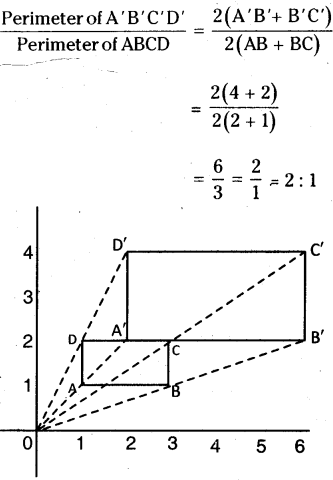
Observe the following dilation ABCD, it is a square drawn on a graph sheet.
All vertices A, B, C, D are joined from the sign ’O’ and produced to 3 times the length upto A’, B’, C’ and D’ respec¬tively. Then A’, B’, C’, D’ are joined to form a rectangle which 3 times has enlarged sides of ABCD. Here, 0 is called centre of dilation and OA′/OA = 3/1 = 3 is called scale factor.
∴ □ ABCD ~ □ A’B’C’D’
[∵ their corresponding sides are equal]

Question 1.
Cut the bold type English alphabets (capital) and paste in your note book. Draw possible number of lines of symmetry for each of the letter.

• (i) How many letters have no linear symmetry?
• (ii) How many letters have one line of symmetry?
• (iii) How many letters have two lines of symmetry?
• (iv) How many letters have more than two lines of symmetry?
• (v) Which of them have rotational symmetry?
• (vi) Which of then have point symmetry?

Solution:

i) letters don’t have line of symmetry
→ F, G, J, L, N, P, Q, R, S, Z.
ii) Liters which are having 1 line of symmetry
→ B, C, D, E, H, I, K, M, 0, T, U, V,
iii) Letirs which are having 2 lines of symmetry
→ H, I, O, X.
iv) Letters which are having more than two lines of symmetry O, X.
v) Letters which are having rotational symmetry
→ B, D, E, H, I, M, 0, S, T, W, X, Z.
vi) Letters which are having point symmetry
→ 0, X, M, W, H, 1, E, D.

Question 2.
Draw lines of symmetry for the following figures. Identify which of them have point symmetry. Is there any implication between lines of symmetry and point symmetry?

Solution

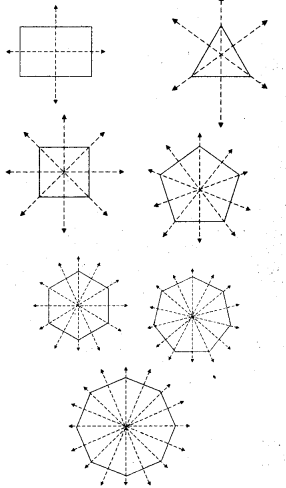
The given figures has point of symmetry. Which are having line of symmetry are also having point of symmetry.

Question 3.
Name some natural objects with faces which have atleast one line of symmetry.

Solution:

1. 1) Moon (Full)
2. 2) Face of a human being
3. 3) Orange fruit
4. 4) Sunflower
5. 5) Butterfly

Question 4.
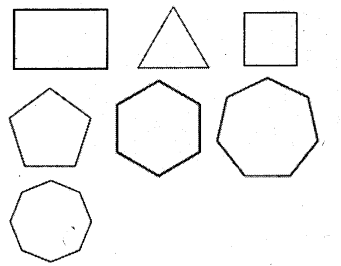
Draw three tessellations and name the basic shapes used on your tessellation.

Solution:
I may notice that the basic shapes used to draw tessellations are pentagon, rectangle, squares, equilateral triangles, hexagons etc. Most tessellations can’t be formed with these shapes.