Question 1.
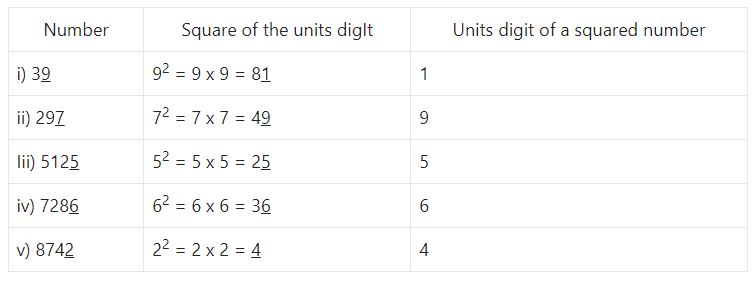
What will be the units digit of the square of the following numbers?
- (i) 39
- (ii) 297
- (iii) 5125
- (iv) 7286
- (v) 8742
Solution:
Question 2.
Which of the following numbers are perfect squares?
- (i) 121
- (ii) 136
- (iii) 256
- (iv) 321
- (v) 600
Solution:

Question 3.
The following numbers are not perfect squares. Give reasons?
- (i) 257
- (ii) 4592
- (iii) 2433
- (iv) 5050
- (v) 6098
Solution:

Question 4.
Find whether the square of the following numbers are even or odd?
- (i) 431
- (ii) 2826
- (iii) 8204
- (iv) 17779
- (v) 99998
Solution:

Question 5.
How many numbers lie between the square of the following numbers
(i) 25; 26
(ii) 56; 57
(iii) 107;108
Solution:
The numbers lie between the square of the numbers are:
1) 25,26 → 2 x 25=50
ii) 56, 57 → 2 x 56 = 112
iii) 107, 108 → 2 x 107 = 214
Question 6.
Without adding, find the sum of the following numbers
(i) 1 + 3 + 5 + 7 + 9 =
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 =
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 =
Solution:
(i) 1 + 3 + 5 + 7 + 9 = (5)2= 5 x 5 = 25
[∵ Sum of ‘n’ consecutive odd number = n2]
(ii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 = 92= 9 x 9 = 81
(iii) 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 + 19 + 21 + 23 + 25 = 132= 13 x 13 = 169
Question 1.
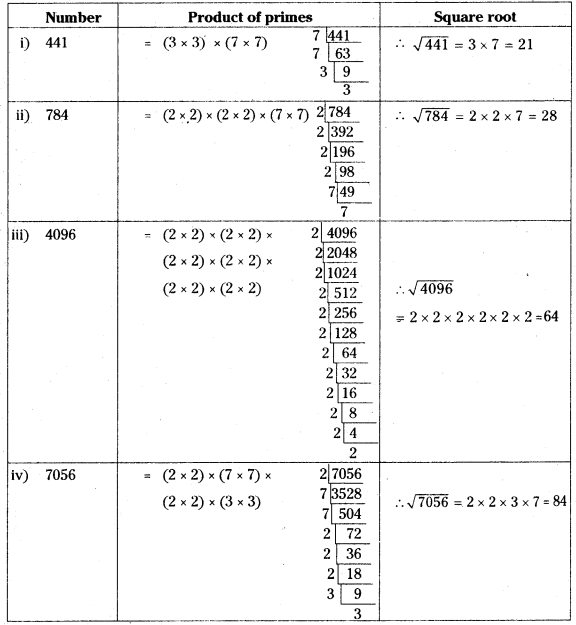
Find the square roots of the following numbers by Prime factorization method.
(i) 441
(ii) 784
(iii) 4096
(iv) 7056
Solution:
Question 2.
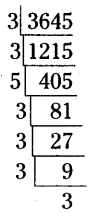
Find the smallest number by which 3645 must be multiplied to get a perfect square.
Solution:
The prime factorization of 3645
= (3 x 3) × (3 x 3) (3 x 3) x 5
∴ Deficiency of one ‘5’ is appeared in the above product.
∴ 3645 is multiplied with 5 then we will get a perfect square.
Question 3.
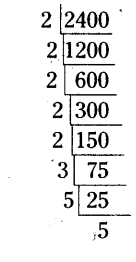
Find the smallest number by which 2400 is to be multiplied to get a perfect square and also find the square root of the resulting number.
Solution:
The prime factorization of 2400
=(2 x 2) x (2 x 2) x 2 x (5 x 5)x 3
∴ 2,3 are needed to form a pair
∴ 2 x 3 = 6
∴ 6 should be multiplied with 2400 then we will get a perfect square number.
∴ 2400 x 6 = 14400
∴ √14400=120
Question 4.
Find the smallest number by which 7776 is to be divided to get a perfect square.
Solution:
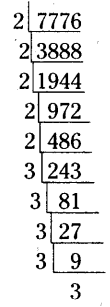
The prime factorization of 7776
=(2 x 2) x (2 x 2) x 2 x(3 x 3) x (3 x 3) x 3
∴ 2, 3 are needed to form a pair
∴ 2 x 3 = 6
∴ 7776 should be divided by 6 then we will get a perfect square number.
Question 5.
1521 trees are planted in a garden in such a way that there are as many trees in each row as there are rows in the garden. Find the number of rows and number of trees in each row.
Solution:
Let the no. of trees planted in a garden for each row = x say.
No. of rows in the garden = x
∴ Total no. of trees in the garden = x x x = x2
According to the sum x2= 1521
x = √1521=√39x39=39
∴ No. of trees for each row = 39
No. of rows in the garden = 39
Question 6.
A school collected ₹ 2601 as fees from its students. If fee paid by each student and number students in the school were equal, how many students were there in the school?
Solution:
Let the no. of students in a school = x say
The (amount) fee paid by each student = ₹ x
Amount collected by all the students
= x × x = x2
According to the sum
∴ x2 = 2601
x =√2601=√51x51 = 51
∴ x = 51
∴ No. of students in the school = 51
Question 7.
The product of two numbers is 1296. If one number is 16 times the other, find the two numbers?
Solution:
Given that the product of two numbers = 1296.
Let the second number = x say
Then first number = 16 x x = 16x
∴ The product of two numbers
= x x 16x= 16x2
According to the sum
16x2= 1296
⇒ x2=1296/16= 81
⇒ x2= 81
⇒x = √81=√9×9= 9
⇒x = 9
∴The first number = 16x
= 16 × 9
=144
The second number = x = 9
Question 8.
7921 soldiers sat in an auditorium in such a way that there are as many soldiers in a row as there are rows in the auditorium. How many rows are there in the auditorium’?
Solution:
Let the number of soldiers sat in an auditorium for each row = x say
∴ No. of rows in an auditorium = x
∴ Total no. of soldiers = x x x = x2
According to the sum,
x2= 7921
x = √7921=√89×89 = 89
∴ No. of rowS in an auditorium = 89
Question 9.
The area of a square field is 5184 m2. Find the area of a rectangular field, whose perimeter is equal to the perimeter of the square field and whose length is twice of its breadth.
Solution:
Area of a square field = 5184 m2
A = s2= 5184
∴ s = √5184=√72×72= 72
∴ s = 72
∴ Perimeter of the square field = 4 × s
= 4 × 72
= 288 m
According to the sum,
Perimeter of a rectangular field
= Perimeter of a square field = 288 m
Let the breadth of a rectangular field
= x m say
∴ Length = 2 × x = 2 × m
∴ Perimeter of the rectangular field
= 2 (1 + b)
= 2 (2x + x)
= 2 × 3x
= 6x
∴ 6x = 288 .
x = 2886
x = 48
∴ Breadth of the rectangular field
= x = 48 m
Length of the rectangular field = 2x
= 2 × 48
=96m
∴ Area of the rectangular field
= l × b
= 96 × 48
= 4608 m2
Question 1.
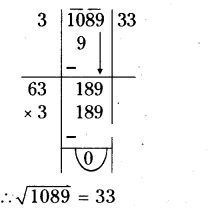
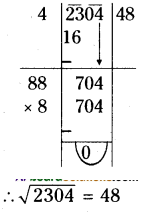
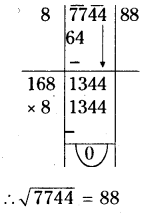
Find the square roots of the following numbers by division method.
- (i) 1089
- (ii) 2304
- (iii) 7744
- (iv) 6084
- (v) 9025
Solution:
(i) 1089
(ii) 2304
(iii) 7744
(iv) 6084
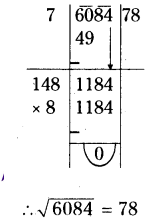
(v) 9025
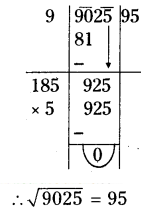
Question 2.
Find the square roots of the following decimal numbers.
- (i) 2.56
- (ii) 18.49
- (iii) 68.89
- (iv) 84.64
Solution:
(i) 2.56
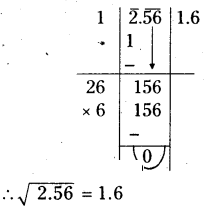
(ii) 18.49
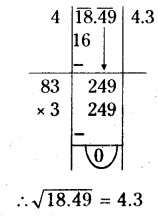
(iii) 68.89
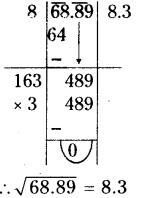
(iv) 84.64
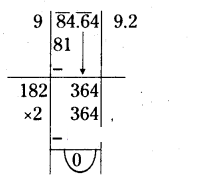
Question 3.
Find the least number that is to be subtracted from 4000 to make it perfect square
Solution:
Square root of 4000 by
Division Method:
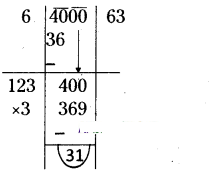
∴ The least number 31 should be subtracted from 4000 we will get a perfect square number4
∴ 4000 - 31 = 3969
= √3969=√63×63= 63
Question 4.
Find the length of the side of a square whose area is 4489 sq.cm.
Solution:
Area of a square (A) = 4489 sq.cms
A = s2
s2 = 4489
s= √4489=√67x67=67cms.
∴ The side of a square (s) = 67cms.
Question 5.
A gardener wishes to plant 8289 plants in the form of a square and found that there were 8 plants left. How many plants were planted in each row?
Solution:
No. of plants are planted = 8289 If 8289 plants are planted in a square shape, 8 plants are left.
Then remaining plants = 8289 - 8 = 8281
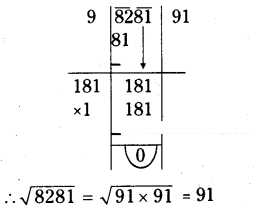
∴ No. of plants for each row = 91
∴ 8281 plants are planted in a square shape then no. of plants are planted for each row = 91
Question 6.
Find the least perfect square with four digits.
Solution:
The smallest number of 4 digits = 1000
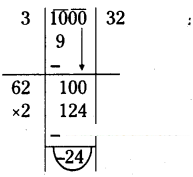
∴ 24 should be added tö 1000 then 1000 + 24 = 1024
∴ The smallest 4 digited perfect square number is 1024.
[∵ √1024= 32]
Question 7.
Find the least number which must be added to 6412 to make it a perfect square?
Solution:
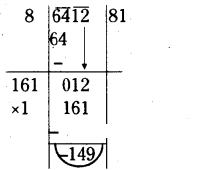


Question 1.
Find the cubes of the following numbers
(1) 8
(ii) 16
(iii) 21
(iv) 30
Solution:
| Number |
Cube Of a Number |
| i) 8 |
83= 8 × 8 × 8 = 512 |
| ii) 16 |
163= 16 × 16 × 16 = 4096 |
| iii) 21 |
213= 21 × 21 × 21 = 9261 |
| iv) 30 |
303= 30 × 30 × 30 = 27000 |
Question 2.
Test whether the given numbers are perfect cubes or not.
(i) 243
(ii) 516
(iii) 729
(iv) 8000
(v)2700
Solution:
| Number |
Cube Of a Number |
Yes / No |
| i) 243 |
3 × 3 × 3 × 3 × 3 = 35 |
No |
| ii) 516 |
2 × 2 × 3 × 43 |
No |
| iii) 729 |
9 × 9 × 9 = 93 |
Yes |
| iv) 8000 |
20 × 20 × 20 = (20)3 |
Yes |
| v) 2700 |
(30) × (30) × 3 |
No |
Question 3.
Find the smallest number by which 8788 must be multiplied to obtain a perfect cube?
Solution:
The prime factorisation of 8788
= (2 × 2) × (13 × 13 × 13)

∴ From the above product 2 is left in the triplet.
∴ 2 should be multiplied with 8788 we will get a perfect cube number.
Question 4.
What smallest number should 7803 be multiplied with so that the product becomes a perfect cube?
Solution:
The prime factorisation of 7803
= (3 × 3 × 3) × (17 × 17)

∴ From the above product 17 is left in
the triplet.
∴ 17 should be multiplied to 7803 then we will get a perfect cube number.
Question 5.
Find the smallest number by which 8640 must be divided so that the quotient is a perfect cube’?
Solution:
The prime factorisation of 8640
= (2 × 2 × 2) × (2 × 2 × 2) × 5 × (3 × 3 × 3)
= (2)3× (2)3× 5 × (3)3

Question 6.
Ravi made a cuboid of plasticine of dimensions 12cm, 8cm and 3cm. How many minimum number of such cuboids will be needed to form a cube’?
Solution:
The volume of a plasticine cuboid
= l × b × h
= 12 × 8 × 3
= 288 cm3
If the minimum no. of such cuboids will be needed to form a cube then its volume be less than 288 i.e., 216 cm3
∴ s3= 216
s=∛216=∛6×6×6=∛63=6
∴ The side of the cube 6 cm
Question 7.
Find the smallest prime number dividing the sum 311+513.
Solution:
The units digit in 311is 7

∴ The units digit in 311 is 7
The units digit in 513is 5
7 + 5 = 12 is divided by a smallest prime number 2.
∴ The smallest prime number that divide the sum 311 + 513 = 2
Question 1.
Find the cube root of the following numbers by prime factorization method.
- (i) 343
- (ii) 729
- (iii) 1331
- (iv) 2744
Solution:
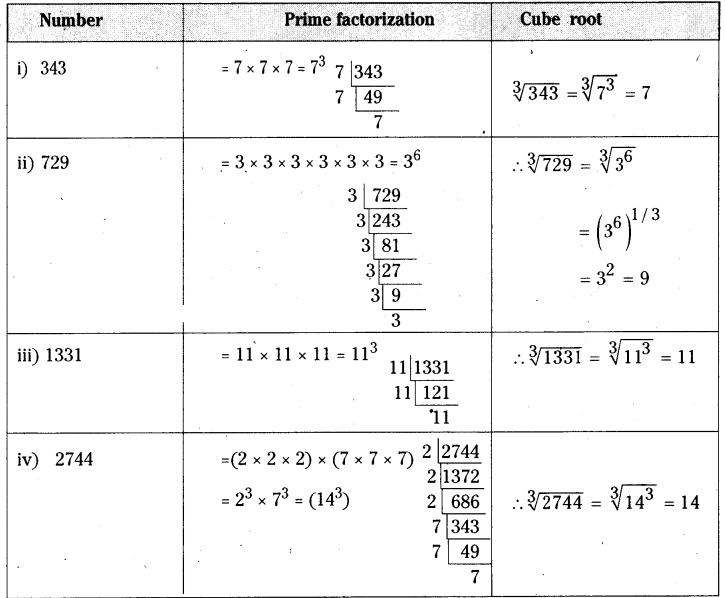
Question 2.
Find the cube root of the following numbers through estimation’?
- (i) 512
- (ii) 2197
- (iii) 3375
- (iv) 5832
Solution:
Step 1: Start making groups of three digits starting from the unit place.
i.e,512 First group is 512
Step 2: First group i.e 512 will give us the units digit of the cube root. As 512 ends with 2, then its cube root ends with 8 (2 x 2 x 2) So the units place of the cube root will be 8.
Step 3: Now take the second group i.e. 0. Which is 03< 1 < 23.
So the least number is ‘0′.
∴ Tens digit of a cube root of a number be 0.
∴ ∛512= 08= 08
(ii) 2197
Step 1: Start making groups of three digits starting from the unit place.

Step 2: First group i.e., 197 will give us the units digit of the cube root.
As 197 ends with 7, its cube root ends with 3. ‘
[∵ 3 x 3 x 3 = 27]
∴ Its units digit is 7.
Step 3: Now take the second group i.e.,2
We know that i3 < 2 < 2
∴ The least number be 1.
∴ The required number is 13.
∴ ∛2197 = ∛13 x 13 x 13 = ↶](13)8
= 13
(iii) 3375
Step 1: Start making groups of three digits starting from the unit place.
i.e.;

Step 2: First group is 375. Its units digit is 5.
∴ The cube root is also ends with 5.
∴ The units place of the cube root will be 5.
Step 3: Now take the second group,
i.e., 3 we know that 13< 33<23
∴ The least number is 1.
∴ The tens digit of a cube root will be 1.
∴ The required number = 15
∛3375 = ∛ 15 x 15 x 15 = √15 = 15
(iv) 5832
Step 1: Start making groups of three digits starting from the unit place.

Step 2: The units digit of 832 is 2.
∴ The cube root of the number ends with units digit 8.
[∵ 8 x 8 x 8 = 512]
Step 3: In the second group i.e., 5 lie between 1 and 6
i.e., 13< 5 < 23
∴ The tens digit of a number will bel.
∴ The required number is 18.
∴ ∛5832 = ∛18 x 18 x 18 = ∛(18)3
= 18
Question 3.
State true or false?
- (i) Cube of an even number is an odd number
- (ii) A perfect cube may end with two zeros
- (iii) If a number ends with 5, then its cube ends with 5
- (iv) Cube of a number ending with zero has three zeros at its right
- (v) The cube of a single digit number may be a single digit number.
- (vi) There is no perfect cube which ends with 8
- (vii) The cube of a two digit number may be a three digit number.
Solution:
- (i) Cube of an even number is an odd number (F)
- (ii) A perfect cube may end with two zeros (F)
- (iii) If a number ends with 5, then its cube ends with 5. (T)
- (iv) Cube of a number ending with zero has three zeros at its right. (T)
- (v) The cube of a single digit number may be a single digit number. (F)
- (vi) There is no perfect cube which ends with 8(F)
- (vii) The cube of a two digit number may be a three digit number. (F)
Question 4.
Find the two digit number which is a square number and also a cubic number.
Solution:
The two digited square and cubic
number is 64
∴ 64 = 8 x 8 = 82⇒ √64 = 8
64 = 4 x 4 x 4 = 43⇒ ∛64 = 4