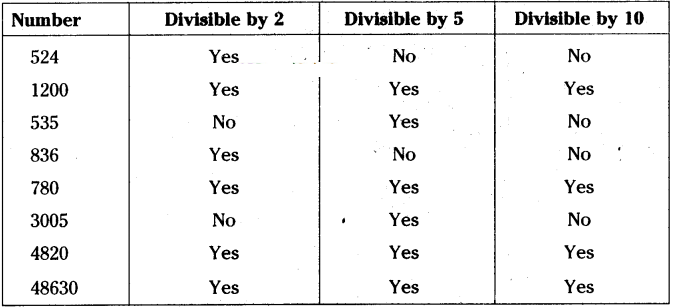
Question 1.
Using divisibility rules, fmd which of the following numbers are divisible by 2,5,10 ( say
yes or no ) in the given table. What do you observe?

Solution
Question 2.
Using divisibility tests, determine which of following numbers are divisible by 2
(a) 2144 (b) 1258 (c) 4336 (d) 633 (e) 1352
Solution:

Question 5.
Write the number of factors of the following’?
(a) 18 (b) 24 (e) 45 (d) 90 (e) 105
Solution:
| Number |
Factors , |
No.of factors |
| a) 18 |
1,2,3,6,9,18 |
6 |
| b) 24 |
1, 2, 3, 4, 6, 8, 12, 24 |
8 |
| c) 45 |
1,3,5,9,15,45 |
6 |
| d) 90 |
1, 2, 3, 5, 6, 9,10, 15, 18, 30, 45, 90 |
12 |
| e) 105 |
1,3, 5, 7,15,21,35,105 |
8 |
Question 6.
Write any 5 numbers which are divisible by 2,5 and 10.
Solution:
10, 20, 30, 40. are divisible by 2, 5 and 10
[∵ The L.C.M. of 2, 5, 10 is 10]
Question 7.
A number 34A is exactly divisible by 2 and leaves a remainder 1, when divided by 5, find A.
Solution:
If 34A Is divisible by 2 then the remainder should be equal to 0.
∴ A should be equal to 0, 2, 4, 6, 8.
∴ 340, 342, 344, 346, 348 are divisible by 2 and gives the remainder ‘0’.
Among these 346 is divisible by 5 and gives the remainder 1.
∴ 346 → 6/5 (R = 1)
∴ The value of A = 6.
Question 1.
If 345 A 7 is divisible by 3,supply the missing digit in place of ‘A’.
Solution:
If the sum of the digits of a number is divisible by 3, then the number is divisible by 3.
∴ 345A7 ⇒ 3 + 4 + 5 + A + 7 = 19 + A
19 + A = 3 x 7
⇒ A = 21 - 19 = 2 ⇒ A = 24 - 19 = 5
A + 19 = 3 x 8
⇒ A = 24 - 19 = 5
A + 19 = 3 x 9
⇒ A = 27 - 19 = 8
∴ A = {2,5,8}
Question 2.
If 2791 A,is divisible by 9, supply the missing digit in place of ‘A’.
Solution:
If the sum of the digits of a number is divisible by 9, then the number is divisible by 9.
∴ 2791A = 2 + 7 + 9 + 1 + A = 9 x 3
⇒ 19 + A = 9 x 3 = 27
⇒ A = 27 - 19 = 8
∴ A = 8
Question 3.
Write some numbers which are divisible by 2,3,5,9 and 10 also.
Solution:
90, 180, 270. are divisible by 2, 3, 5, 9 and 10.
[∵ The L.C.M. of 2, 3, 5, 9, 10 is 90]
Question 4.
2A8 is a number divisible by 2, what might be the value of A’?
Solution:
If the units digit of a number be 0, 2, 4, 6, 8 then it is divisible by 2.
∴ 2A8 is divisible by 2 for any value of A.
∴ A = (0, 1, 2 ………………….9)
Question 5.
50B is a number divisible by 5, what might be the value of B?
Solution:
Given number is 50B.
The units digit of a number ¡s either ‘0’ or 5, then it is divisible by 5.
∴ 500 → 0/5 (R = 0)
505 → 5/5 (R = 0)
∴ B = {0, 5}
Question 6.
2P is a number which is divisible by 2 and 3, what is the value of P
Solution:
The given number is 2P.
If 2P is divisible by 2, 3 then 2P should be a multiple of 6. [ ∵ L.C.M. of 2, 3 is 6]
∴ 2P = 24, 30 ………….
24 → 2 + 4 → 6/3 (R = 0)
∴ P = 4
Question 7.
54Z leaves remainder 2 when divided by 5 , and leaves remainder 1 when divided by 3, what is the value of Z’?
Solution:
If 54Z is divisible by 3 then the sum of the digits of the number is divisible by 3.
According to problem 54Z is divisible by 3 and leaves remainder 1’.
∴ 5 + 4 + Z = (3 x 4) + 1
= 9 + Z = 13
∴ Z = 4(or)
9 + Z = (3 x 5) + 1
9 + Z = 16
Z = 7
If 54Z is divisible by 5 then Z should be equal to either ‘0’ or ‘5’.
∴ 54(0 + 2) = 542 (Z = 2)
54(0 + 7) = 547 (Z = 7)
∴ From the above two cases
Z = 7
∵ 547 → 7/5 (R = 2)
Question 8.
27Q leaves remainder 3 when divided by 5 and leaves remainder 1 when divided by 2, what is the remainder when it is divided by 3?
Solution:
27Q is divided by 5 gives the remainder 3
Le.,27Q = 27 (0 + 3) = 273(Z = 3)(T)
= 27 (0 + 8) = 278 (Z = 8)
27Q is divided by 2 gives the remainder 1.
i.e., 27Q = 27(0 + 1) = 271 (Z = 1)
27Q = 27 (0 + 3) = 273 (Z = 3) (T)
∴ From above situations Z = 3
∴ 27Q = 273 → 2 + 7 + 3 → 12/3 (R = 0)
∴ 273 is divisible by 3 and gives the remainder 0’.
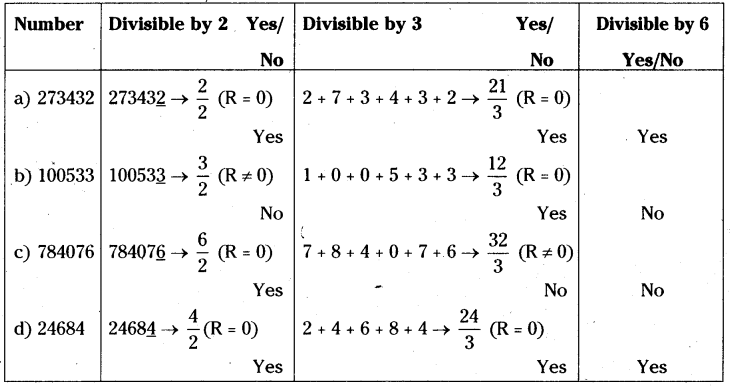
Question 1.
Check whether the given numbers are divisible by ‘6’ or not?
(a) 273432
(b) 100533
(c) 784076
(d) 24684
Solution:
if a number is divisible by ‘6’, it has to be divisible by 2 and 3.
Question 2.
Check whether the given numbers are divisible by ‘4’ or not?
(a) 3024
(b) 1000
(c) 412
(d) 56240
Solution:
| Number |
Divisible by 4 |
Yes/No |
| a) 3024 |
3024 → 24/4 (R = 0) |
Yes |
| b) 1000 |
1000 → 0/4 (R = 0) |
Yes |
| c) 412 |
412 → 12/4 (R = 0) |
Yes |
| d) 56240 |
56240 → 40/4 (R = 0) |
Yes |
Question 3.
Check whether the given numbers are divisible by ‘8’ or not?
(a) 4808
(b) 1324
(c) 1000
(d) 76728
Solution:
| Number |
Divisible by 4 |
Yes/No |
| a) 4808 |
4808 → 808/8 (R = 0) |
Yes |
| b) 1324 |
1324 → 324/8 (R ≠ 0) |
No |
| c) 1000 |
1000 → 0/8 (R = 0) |
Yes |
| d) 76728 |
76728 → 728/8 (R = 0) |
Yes |
Question 4.
Check whether the given numbers are divisible by ‘7’ or not?
(a) 427
(b) 3514
(e) 861
(d) 4676
Solution:

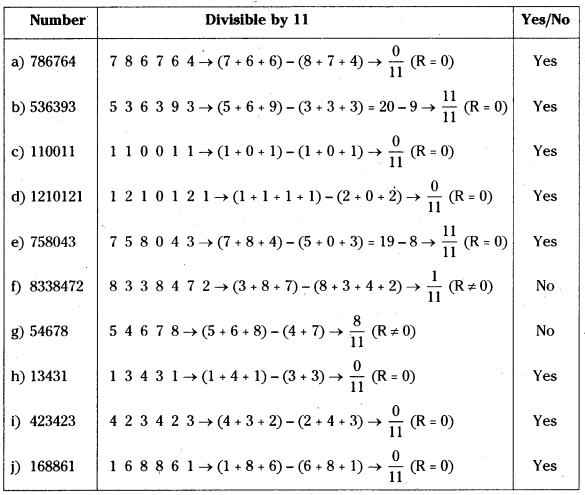
Question 5.
Check whether the given numbers are divisible by ‘11’ or not?
(a) 786764
(b) 536393
(c) 110011
(d) 1210121
(e) 758043
(f) 8338472
(g) 54678
(h) 13431
(i) 423423
(j) 168861
Solution:
Question 6.
If a number is divisible by ‘8’, then it also divisible by ‘4’. also Explain?
Solution:
If a number is divisible by 8 it ¡s also divisible by 4.
∴ If a number is divisible by 8, then it ¡s also divisible by the factors of 8.
Factors of 8 = 1, 2, 4, 8.
∴ The number which is divisible 8, is also divisible by 4.
Question 7.
A 3-digit number 4A3 is added to another 3-digit number 984 to give four digit number 13B7, which is divisible by 11. Find (A + B).
Solution:
The given 3 - digited numbers are = 4A3, 984
∴ 4A3 + 984 = 13B7. If It is divisible by 11 then,
⇒ 1 3 B 7
(1 + B) - (3 + 7)
⇒ (B+1) - 10 = 0 ⇒ B - 9 = 0
∴ B = 9

⇒ A + 8 = 9 ⇒ A = 9 - 8 = 1
∴ A = 1
A + B= 1+9
∴ A + B = 10
Question 1.
Check whether 25110 is divisible by 45.
Solution:
The given number = 25110
If 25110 is divisible by 45 then it should be divisible by 5 and 9.

∴ The number 25110 is divisible by 45
Question 2.
Check whether 61479 is divisible by 81.
Solution:
If 61479 is divisible by 81 then it is divisible by 9.
If the sum of the digits of a number is divisible by 9 then the entire number is divisible by 9.
∴ 61479 → 6 + 1 + 4 + 7 + 9 → 27/9 (R = 0)
∴ 61479 is divisible by 81. [∵ 9 is factor of 81]
Question 3.
Check whether 864 is divisible by 36? Verif,’ whether 864 is divisible by all the factors of 36 ?
Solution:
864 is divisible by 2 and 3.
∴ 864 is divisible by 6.
∴ 864 is divisible by 36 [ ∵ 6 is the factor of 36]
∴ Factors of 36 = 1, 2, 3, 4, 6, 9, 12, 18. 36.


∴ 864 is divisible by all the factor of 36.
Question 4.
Check whether 756 is divisible by 42? Verify whether 756 is divisible by all the factors of 42?
Solution:
756 is divisible by 2 and 3.
∴ 756 is divisible by 6.
2a + 3b + c = 2 x 7 + 3 x 5 + 6 = 14 + 15 + 6 → 35/7 (R = 0)
∴ 756 is divisible by 7.
∴ 756 is divisible by 42. [ ∵ 6, 7 are the factors of 42]
Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42.
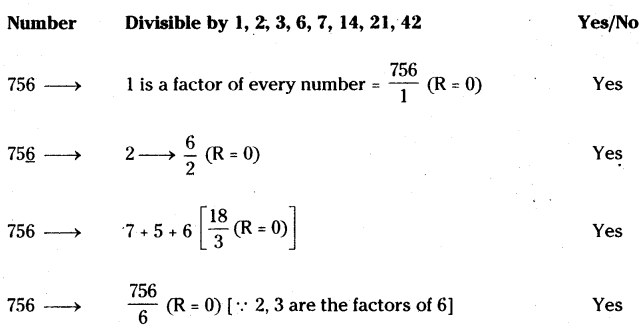

∴ 756 is divisible by all the factor of 42.
Question 5.
Check whether 2156 is divisible by 11 and 7? Verify whether 2156 is divisible by product of 11 and 7?
Solution:
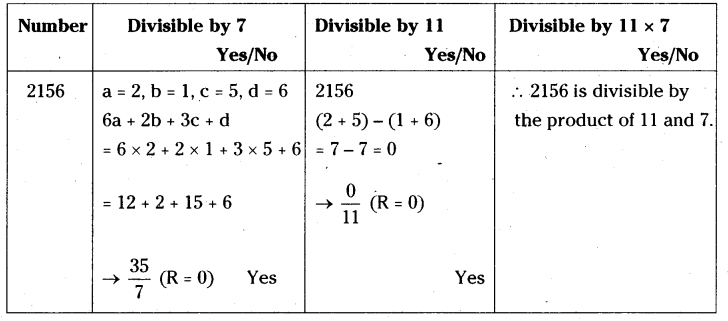
Question 6.
Check whether 1435 is divisible by 5 and 7? Verify if 1435 is divisible by the product of 5 and 7?
Solution:

Question 7.
Check whether 456 and 618 are divisible by 6’? Also check whether 6 divides the sum of 456 and 618 ‘?
Solution:

Question 8.
Check whether 876 and 345 are divisible by 3. Also check whether 3 divides the difference of 876 and 345?
Solution:
| Number |
Divisible by 3 |
Y/N |
Difference is divisible by 3 Y/N |
| 876 |
8 + 7 + 6 → 21/3 (R = 0) |
Yes |
876 - 345 = 531 |
| 345 |
3 + 4 + 5 → 12/3 (R = 0) |
Yes |
The difference of 876, 345 is divisible by 3. |
| 531 |
5 + 3 + 1 → 9/3 (R = 0) |
Yes |
|
Question 9.
Check whether 22 + 23+24 is divisible by 2 or 4 or by both 2 and 4’?
Solution:
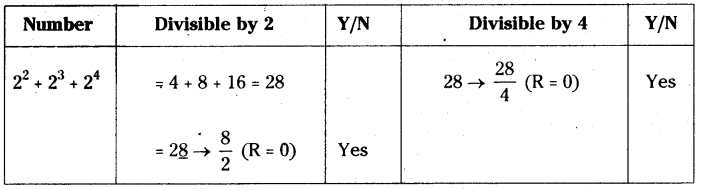
∴ 22 + 23+24 is divisible by both 2 and 4.
Question 10.
Check whether 322 is divisible by 4 or 8 or by both 4 and 8’?
Solution:
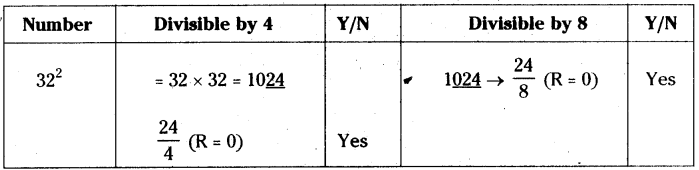
322is divisible by 4 and 8
Question 11.
If A679B is a 5-dit number is divisible by 72 find ‘A’ and ‘B”?
Solution:
If A679B is divisible by 72 then it should be divisible by 8 and 9.
[ ∵ 8, 9 are the factors of 72]
A679B is divisible by 9 then
A + 6 + 7 + 9 + B = A + B + 22 = 27 (= 9 x 3)
=A + B = 5 ……………. (1)
A679B → 79 B/8 [From B (2,4,6,8) we take B = 2]
=792/8 (R = 0)
∴ B = 2
From (1) ⇒ A + 2 = 5
∴ A = 3, B = 2
Question 1.
Find the missing digits in the following additions.
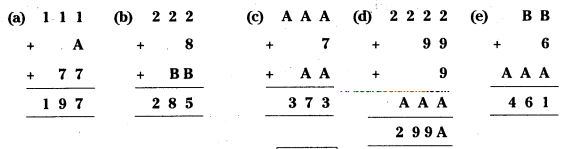
Solution:
a) 1 + A + 7 = 17 ⇒ A = 17 - 8 = 9
∴ A = 9
b) 2 + 8 + B = 15 ⇒ B = 15 - 10 = 5
2 + 1 + B = 8 ⇒ B = 8 - 3 = 5
∴ B = 5
c) A + 7 + A=13 ⇒ 2A = 6 ⇒ A = 3 A + A + 1 = 7 2A = 6 ⇒ A = 3
∴ A = 3
d) From 1st column
2 + 9 + 9 + A = 26
A = 26 - 20 = 6
From 2nd column
⇒ 2 + 1 + A = 9 ⇒ A = 9 - 3 = 6
∴ A = 6
e) B + 6 + A = 11 or 21
B + A + (1 or 2) = 6
A + 1 = 4 ⇒ A = 3
⇒ From (1), B + 6 + 3 = 11 ⇒ B = 2
∴ A = 3, B = 2
Question 2.
Find the value of A in the following
(a) 7A - 16 = A9 (b) 107 - A9 = lA (e) A36 - 1A4 = 742
Solution:
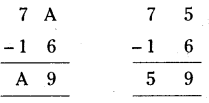
a) 7A - 16 = A9
A- 6 = 9
If A = 5 it is possible.
∴ A = 5 (or)
7A- 16 = A9
⇒ 7 x 10 + (1 x A) - 16 = (A x 10 + 9 x 1)
⇒ 70 + A - 16 = 10A + 9
⇒ 9A = 45
⇒ A = 5
b) 107 - A9 = 1A
⇒107 - (10 x A + 9 x 1) = (1 x 10 + A x 1)
⇒107-10A-9= 10 +A
⇒ 11A = 88 A = 8
c) A36 - 1A4 = 742
⇒ (100 x A + 3 x 10 + 6 x 1) - (1 x 100 + A x 10 + 4 x 1) = 742
⇒ 100A + 36 - 100 - 10A - 4 = 742
⇒ 90A = 810
⇒A = 810/90
∴ A = 9
Question 3.
Find the numerical value of the letters given below-
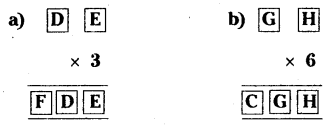
Solution:
a) If E x 3 = E then E should be equal to 0 (or) 5.
5 x 3 = 15, 0 x 3 = 0
3 x D + 0 = ID [If E = 0]
⇒ 3D = 10 + D
⇒ 2D = 10
⇒ D = 5

∴ F = 1, D = 5, E = 0
b) If H x 6 = H then H should be equal to 0, 2, 6, 8.
G6 = 1G [If H = 0]
⇒ 6G + 0 = 10 + G
⇒ 5G = 10
⇒ G = 10/5 = 2
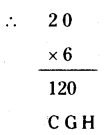
C = 1, G = 2, H = 0

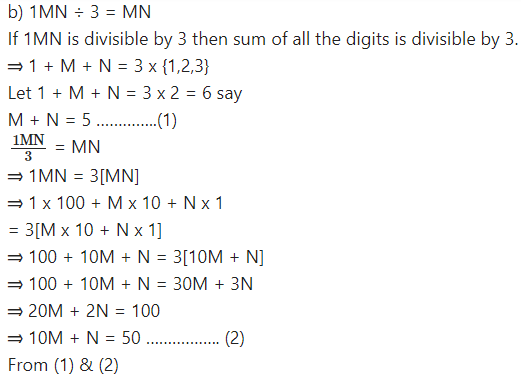
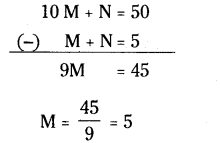
10 M + N = 50 (-) M + N = 5 9M = 45
∴ M = 5
If M = 5 then
M + N = 5
⇒ N = 0
M = 5, N = 0 [∵ 1503 = 50 ]
Question 5.
If ABB x 999 = ABC 123 (where A, B, C are digits) find the values of A, B, C.
Solution:
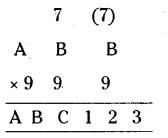
From ABB x 999 = ABC 123, the product of units digit is equal to 3.
∴ B x 9 = 3 is the units digit.
If B = 7 then,
7 x 9 = 6 3

∴ A = 8, B = 7, C = 6
∴ The required product = 876123
∴ A = 8, B = 7, C = 6
Question 1.
Find the sum of integers which are divisible by 5 from 1 to 100.
Solution:
Numbers which are divisible by 5 from 1 to 100 are 5, 10, 15, …………………95, 100.
∴ Sum of the above numbers = 5+10 + ……………..+ 95 + 100
= 5[1 + 2 + ………………….+ 20]

Question 2.
Find the sum of integers which are divisible by 2 from 11 to 50.
Solution:
Numbers which are divisible by 2 from 11 to 50 are 12, 14,48, 50.
Sum of the numbers = 12 + 14 + ……….. + 48 + 50 ‘
= (2 + 4 + ……….. + 50) – (2 + 4 + ……….. + 10)
= 2(1 + 2 +……….. + 25) – 2 (1 + 2 + ……….. + 5)
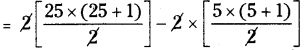
= 25 × 26 - 5 × 6
= 650 - 30
= 620
Question 3.
Find the sum of integers which are divisible by 2 and 3 from 1 to 50.
Solution:
Numbers which are divisible by 2 and 3 i.-e., which are divisible by 6 from 1 to 50 are 6,12 …………….48.
Sum of the numbers = 6 + 12 + ……..+ 48
= 6(1 + 2 +……… + 8)
Question 4.
(n3 - n) is divisible by 3. Explain the reason.
Solution:
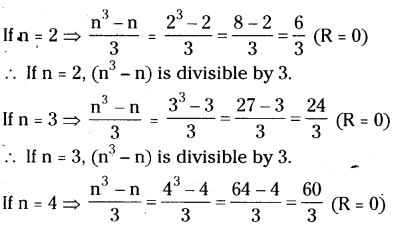
∴ If n = 4, (n3- n) is divisible by 3.
∴ (n3- n) is divisible by all the values of n.
Method 2:
n3 - n = n(n2- 1)
= n(n + 1)(n - 1)
∴ (n3 - n) is divisible by ‘3’ for all the values of n.
[∵ (n - 1), n, (n + 1) are three consecutive odd numbers]
Question 5.
Sum of ‘n’ odd number of consecutive numbers is divisible by ‘n’. Explain the reason.
Solution:
Sum of n’ consecutive odd numbers = n2
Since n is a factor of n2, It Is divisible by ‘n’.
Question 6.
Is 111+ 211+ 311+ 411divisible by 5? Explain.
Solution:
Sum of units digit of number 111+ 211+ 311+ 411
= 1 + 8 + 7 + 4
= 20 → 20/5 (R = 0)
∴ 111+ 211+ 311+ 411is divisible by 5.
Question 7.

Find the number of rectangles of the given figure?
Solution:
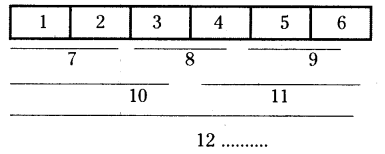
∴ No.of rectangles in the given figure = 1 + 2 + 3 + 4 + 5 + 6 = 21
Question 8.
Rahul’s father wants to deposit sorne amount of money every year on the day of Rahul’s birthday. On his 1st birth day Rs.100, on his 2nd birth day Rs.300, on his 3 birth day Rs.600, on his 4th birthday Rs. 1000 and so on. What is the amount deposited by his father on Rahul’s 15th birthday.
Solution:

Rahul’s father deposits on every year 200, 300, 400 more than before year.
Then he deposits ₹ 10,500 on 14th birthday.
∴ The amount deposits on 15th birthday
= 10,500 + 1,500
= ₹ 12,000/-
Question 9.
Find the sum of integers from 1 to 100 which are divisible by 2 or 5.
Solution:
Sum of the numbers which are divisible by 2 from 1 to 100
= 2 + 4 + ……….. + 100
= 2(1 + 2 + ………… +50)
= 2 × 50×(50+1)/2
= 50 × 51 = 2550
Sum of the numbers which are dMsible by 5froin I to 100
= 5 + 10 + ……….. + 100
= 5(1 + 2 +……….. +20)
= 5 × 20×(20+1)/2
=5 × 10 × 21
=1050
Sum of the numbers which are.divisible by both 2 and 5 = 2550 + 1050 =3600
∴ Sum ol the numbers which are divisible by 2 or 5 from 1 to 100
= 10 + 20 + ………..+ 100 ( L.C.M of 2, 5 is 10)
=10(1 + 2 + ………..+ 10)
= 10 × 10×(10+1)/2
= 5 × 10 × 11 .
= 550
∴ The sum of required numbers 3600-550 3050
Question 10.
Find the sum of integers from 11 to 1000 which are divisible by 3.
Solution:
Sum ol the numbers which are divisible by 3 from lito 1000
= 12 + 15+ ……….. +099
= 3(4 + 5 + ……….. +333)
= 3(1 + 2 + ……….. + 333) - 3(1 + 2+3)
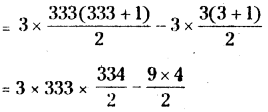
= 999 × 167 - 9 × 2
= 166833 - 18
= 166815