Question 1.
There are two cuboidal boxes as shown in the given figure. Which box requires the less amount of material to make?
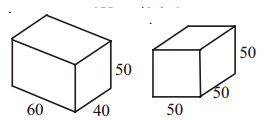
Solution:
Volume of a cuboid V1= lbh
= 60 × 40 × 50
V1= 1,20,000 cubic units.
Volume of a cube V2= (a)3
= (50)3= 50 × 50 × 50
V2= 1,25,000 cubic units.
∴ The cuboidal box requires less amount of material.
∴ V1< V2
Question 2.
Find the side of a cube whose surface area is 600 cm2
Solution:
Total surface area of a cube = 6a2
⇒ 6a2= 600
⇒ a2=[latex]600/6[/latex] = 100
⇒ a2= 100
⇒ a = √100 = 10
∴ The side of a cube (a) = 10 cm.
Question 3.
Prameela painted the outer surface of a cabinet of measures 1m × 2m × 1 .5m. Find the surface area she cover if she painted all except the bottom of the cabinet?
Solution:
The area of outer surface of a cabinet except the bottom of the cabinet will be equal to its lateral surface area.
I = lm,b = 2m, h = 1.5m.
A = 2h(l + b)
= 2 × 1.5(1 + 2)
= 3 × 3 = 9 m2.
Question 4.
Find the cost of painting a cuboid of dimensions 20cm × 15 cm × 12 cm at the rate of 5 paisa per square centimeter.
Solution:
l = 20cm, b = 15cm, h = 12cm.
∴ Total surface area of a cuboid
A = 2 (lb + bh + lh)
=2(20 × 15 + 15 × 12 + 20 × 12)
= 2 (300 + 180 + 240)
= 2 × 720
= 1440 sq.cm.
The cost of painting a cuboid at the rate of 5 paisa per sq. cm for 1440 sq.cm.
= 1440 × 5 paisa
= 7200 paise
= ₹7200/100
= ₹ 72
Question 1.
Find the volume of the cuboid whose dimensions are given below.
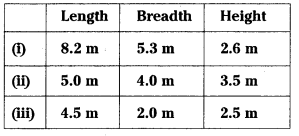
Solution
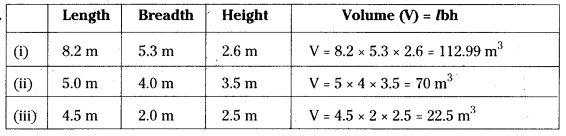
Question 2.
Find the capacity of the tanks with the following internal dimensions. Express the capacity in cubic meters and litres for each tank.

Solution
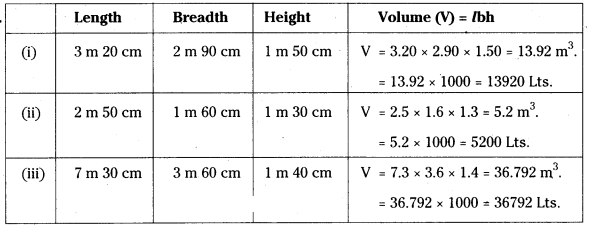
Question 3.
What will happen to the volume of a cube if the length of its edge is reduced to half? Is the volume get reduced? If yes, how much?
Solution:
Volume of a cube of side (s) is V1= a3
If the length of the side is reduced by half then
s =a/2
∴ Volume of cube (V2) = s3
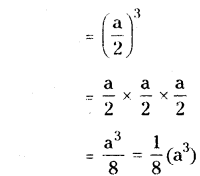
∴ V2=1/8 × V1
∴ V1= 8V2
Question 4.
Find the volume of each of the cube whose sides are.
(i) 6.4 cm
(ii) 1.3 m
(iii) 1.6 m.
Solution:
Volume of a cube(V) = a3
i) a = 6.4 cm
ii) a = 1.3 m
iii) a = 1.6 m
V = (6.4)3
Volume of a cube (V) = a3
= 6.4 × 6.4 × 6.4
= 262.144 cm3
V = (1.3)3
= 1.3 × 1.3 × 1.3
= 2.197 m3
V = (1.6)3
= 1.6 × 1.6 × 1.6
= 4.096 m3
Question 5.
How many bricks will be required to build a wall of 8 m long, 6m height and 22.5 cm thici if each brick measures 25 cm by 11.25 cm by 6 cm?
Solution:
The volume of a wall of measures
8 m × 22.5 cm × 6 m
(V1) = l1b1h1
= 8 m × 22.5 cm × 6 m
= 800 cm × 22.5 cm × 600 cm
The volume of a brick each measures
25 cm × 11.25 cm × 6 cm
(V2) = l2b2h2
= 25 × 11.25 × 6 cm3
∴ The no.of bricks will be required
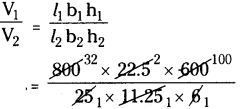
= 32 × 2 × 100 = 6400
Question 6.
A cuboid is 25 cm long, 15 cm broad, and 8 cm high . How much of its volume will differ from that of a cube with the edge of 16 cm’?
Solution:
Volume of a cuboid (V1) of measures
= 25 cm, b = 15 cm, h = 8 cm.
V1= 25 × 15 × 8 = 3000 cm3
Volume of a cube of measure side (s) = 16 cm is
V2= (s)3= (16)3= 16 × 16 × 16
= 4096 cm3
The difference between their volumes
= V2- V1
= 4096 - 3000
= 1096 cm3
Question 7.
A closed box is made up of wood which is 1cm thick .The outer dimensions of the box is 5 cm × 4 cm × 7 cm. Find the volume of the wood used.
Solution:
The volume of a box formed with outer measures 5 cm × 4 cm × 7 cm
V1= l × b × h
= 5 × 4 × 7
∴ V1= 140 cm3
Inner measures
= l - 2w, b - 2w, h - 2w
= (5 - 2 × 1), (4 - 2 × 1), (7 - 2 × 1)
= (5 - 2), (4 - 2), (7 - 2)
= 3 cm, 2 cm, 5 cm
∴ Volume of a box formed with inner measures
V2= (l - 2w)(b - 2w)(h - 2w)
= 3 × 2 × 5 = 30 cm3
∴ The volume of wood used = V1- V2
= 140 - 30 = 110 cm3
Question 8.
How many cubes of edge 4cm, each can be cut out from cuboid whose length, breadth and height are 20 cm, 18 cm and 16 cm respectively
Solution:
The volume of a cuboid formed with the measures 20 cm × 18 cm × 16 cm
(V1) = l1b1h1= 20 × 18 × 16
Volume of a cube (V2) = s3
s = 4 cm (given)
∴ V2= (s)3= (4)3= 4 × 4 × 4 cm3
∴ No.of cubes are required
=V1/V2=20×18×16/4×4×4
= 90
Question 9.
How many cuboids of size 4 cm × 3 cm × 2 cm can be made from a cuboid of size 12 cm x 9cm x 6cm?
Solution:
Volume of a cuboid of measures 12 cm × 9 cm × 6 cm
V1= l × b × h = 12 × 9 × 6
Volume of the smaller cuboid of measures 4 cm × 3 cm × 2 cm
V2= l2b2h2= 4 × 3 × 2
∴ No.of cuboids are made
=V1/Vi = 12×9×6/4×3×2= 27
Question 10.
A vessel in the shape of a cuboid is 30 cm long and 25 cm wide. What should be its height to hold 4.5 litres of water ?
Solution:
Length of a cuboidal vessel (l) = 30 cm
breadth (b) = 25 cm
height (h) = ?
The volume of water m a cuboidal vessel = 4.5 Lts.
= 4.5 × 1000 cm3
= 4500 cm3
∴ l × b ×h = 4500
⇒ 30 × 25 × h = 4500
⇒h =4500/30×25
∴ h = 6 cm
∴ Height of the vessel (h) = 6 cm