Question 1.
Draw the following 3-D figures on isometric dot sheet.
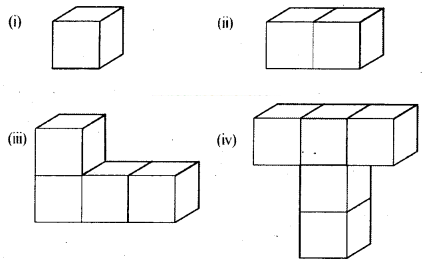
Solution
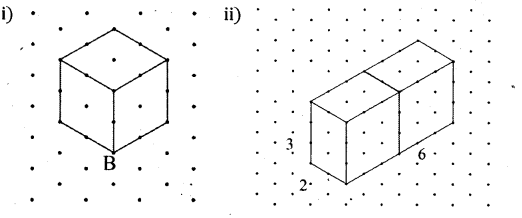
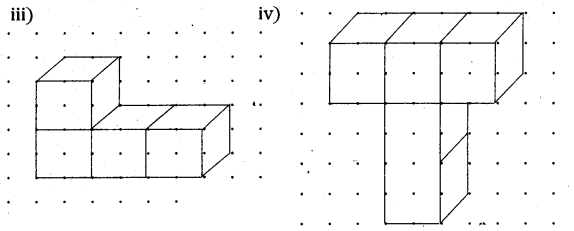
Question 2.
Draw a cuboid on the isometric dot sheet with the measurements 5 units × 3 units × 2 units.
Solution:
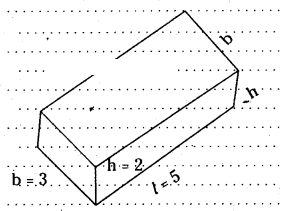
Question 3.
Find the number of unit cubes in the following 3-D figures.
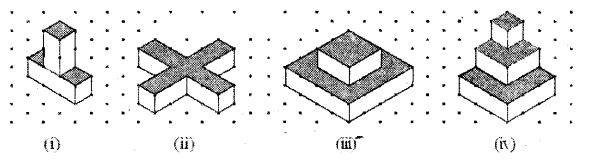
Solution:
| Figure |
No. of cubes |
| i) |
2 + 3 = 5 |
| ii) |
2 × 4 + 1 = 9 |
| iii) |
4 + 16 = 20 |
| iv |
1 + 4 + 9 = 14
|
Question 4.
Find the areas of the shaded regions of the 3-D figures given in question number 3.

Solution:
| Figure |
Area of the shaped regions |
| i) |
3 × 1 × 1 =3 Sq. Units. |
| ii) |
4(2 × 1) + 1 = 9 Sq. Units. |
| iii) |
4 + (16 - 8) = 4 + 8= 12 Sq. Units. |
| iv) |
1 + (4 - 1) ÷ (9 - 4) = 1 + 3 + 5 = 9 Sq.Units. |
Question 5.
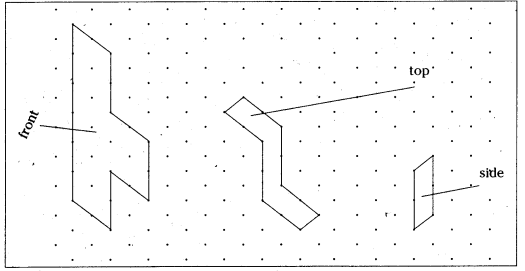
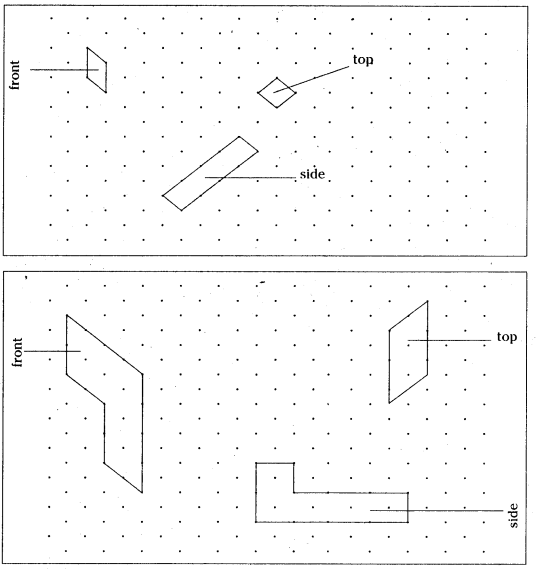
Consider the distance between two consecutive dots to be 1 cm and draw the front view, side view and top view of the following 3-D figures.
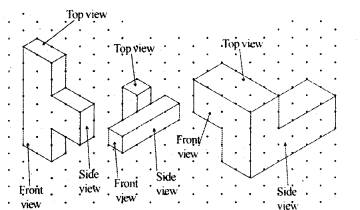
Solution
Question 1.
Count the number of faces , vertices , and edges of given polyhedra and verify Euler’s formula.
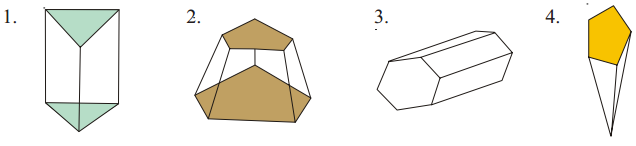
Solution
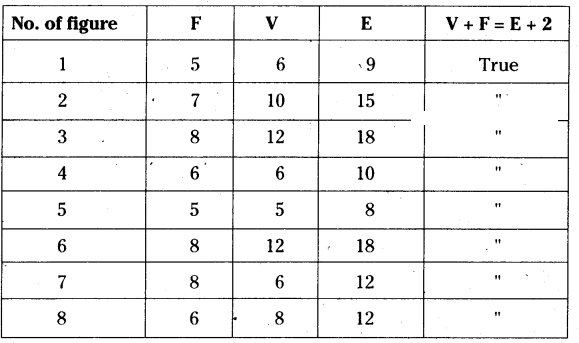
Question 2.
Is a square prism and cube are same? explain.
Solution:
All cubes are square prisms, but converse is not true. (i.e.,) All square prisms are either cubes or, not.
Question 3.
Can a polyhedra have 3 triangular faces only? explain.
Solution:
Any polyhedra can’t have 3 triangular faces because the triangular pyramids are formed starts with 4 faces. So it does not exist.
Question 4.
Can a polyhedra have 4 triangular faces only? explain.
Solution:
Yes, a triangular pyramid have 4 triangular faces.
Question 5.
Complete the table by using Euler’s formula.
| F |
8 |
5 |
? |
| V |
6 |
? |
12 |
| E |
? |
9 |
30 |
Solution:
| F |
8 |
5 |
20 |
| V |
6 |
6 |
12 |
| E |
12 |
9 |
30 |
i) E = V + F- 2 = 8 + 6- 2 = 12
ii) V = E + 2- F = 9 + 2- 5 = 6
iii) F = E + 2- V = 30 + 2-12 = 20
Question 6.
Can a polyhedra have 10 faces ,20 edges and 15 vertices?
Solution:
No. of faces = 10
No. of edges = 20
No. of vertices = 15
According to Euler’s formula E = V + F – 2
⇒ 20 = 15 + 10 - 2
20 = 25 - 2
20 = 23 (False)
∴ A polyhedra doesn’t exist with 10 faces, 20 edges, 15 vertices.
Question 7.
Complete the following table
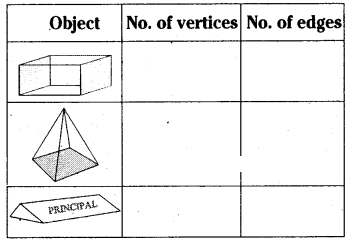
Solution
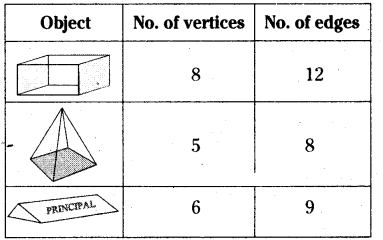
Question 8.
Name the 3-D objects or shapes that can be formed from the following nets.

- (i) Hexagonal pyramid
- (ii) Cuboid
- (iii) Pentagonal pyramid
- (iv) Cylinder
- (v) Cube
- (vi) Hexagonal pyramid
- (vii) Trapezoid
Question 9.
Draw the following diagram on the check ruled book and fmd out which of the following diagrams makes cube?
(i)
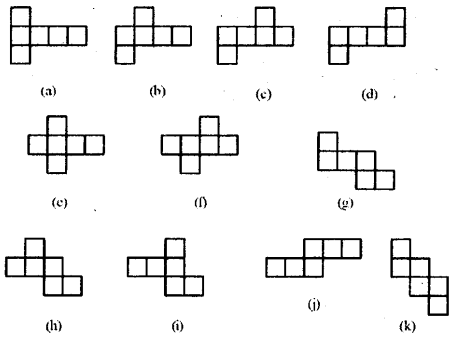
Solution:
The diagrams which makes cubes are a, b, c, e.
(ii) Answer the following questions.
- (a) Name the polyhedron which has four vertices, four faces’?
- (b) Name the solid object which has no vertex?
- (c) Name the polyhedron which has 12 edges’?
- (d) Name the solid object which has one surface’?
- (e) How a cube is different from cuboid?
- (f) Which two shapes have same number of edges, vertices and faces?
- (g) Name the polyhedron which has 5 vertices and 5 faces’?
Solution:
- (a) Tetrahedron
- (b) Sphere
- (c) Cube/Cuboid
- (d) Sphere
- (e) Cube is a regular polyhedron where cuboid is not.
- (f) Cube, Cuboid
- (g) Square pyramid
(iii) Write the names of the objects given below
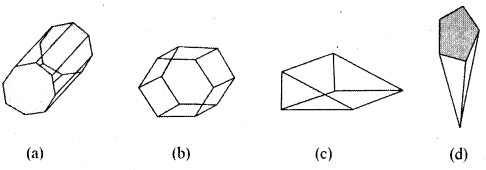
Solution:
- (a) Octagonal prism
- (b) Hexagonal prism
- (c) Triangular prism
- (d) Pentagonal prism