Question 1.
Find the product of the following pairs:
- (i) 6, 7k
- (ii) - 31, - 2m
- (iii) -5t2- 3t2
- (iv) 6n, 3m
- (v) - 5p2, - 2p
Solution:
The product of 6, 7k = 6 × 7k = 42k
- ii) The product of - 3l, - 2m = (- 3l) × (- 2m) = 6/m
- iii) The product of - 5t2, - 3t2= (- 5t2) × (- 3t2) = 15t4
- iv) The product of 6n, 3m = 6n × 3m = 18mn
- v) The product of - 5p2, - 2p = (- 5p2) × (- 2p) = 10p3
Question 2.
Complete the table of the products.
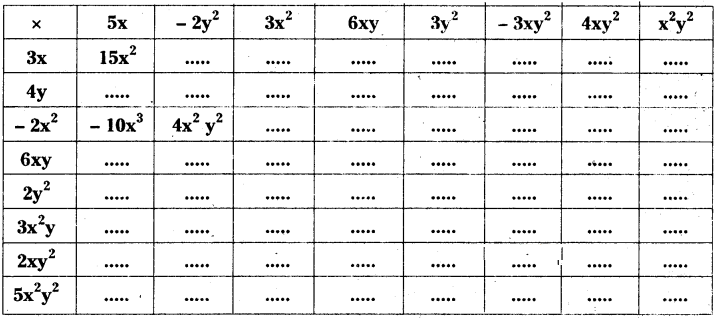
Solution:
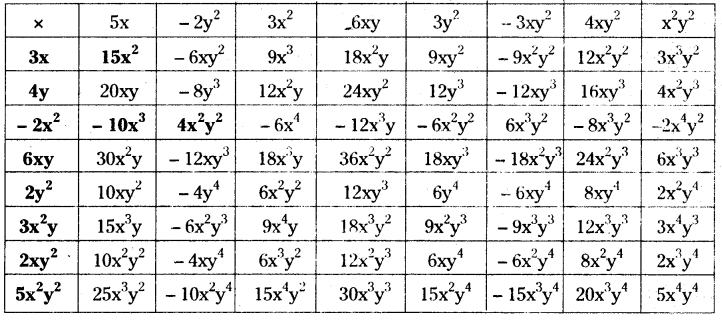
Question 3.
Find the volumes of rectangular boxes with given length, breadth and height in the following table.

Solution:
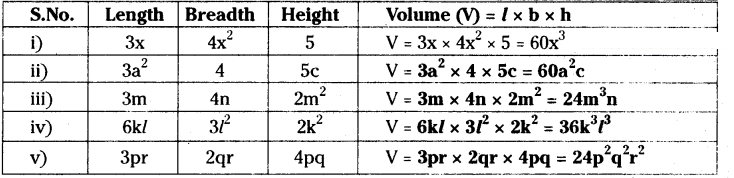
Question 4.
Find the product of the following monomials
(i) xy, x2y , xy, x
(ii) a, b, ab, a3 b, ab3
(iii) kl, lm, km, klm
(iv) pq ,pqr, r
(v) - 3a, 4ab, - 6c, d
Solution:
i) The product of xy, x2y, xy, x = xy × x2y × xy × x
= x5 × y3= x5y3
ii) The product of a, b, ab, a3b, ab3= a × b × ab × a3b × ab3
= a6× b6= a6b6
iii) The product of kl, lm, km, klm = kl × lm × km × klm
k3× l3 × m3=k3l3m3
iv) The product of pq, pqr, r = pq × pqr × r
= p2 × q2× r2- p2q2r2
v) The product of - 3a, 4ab, - 6c, d = (- 3a) × 4ab × (- 6c) x d
= + 72a2× b × c × d
= 72a2bcd
Question 5.
If A = xy,B = yz and C = zx, then find ABC=
Solution:
ABC = xy × yz × zx = x2y2z2
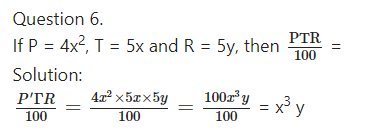
Question 7.
Write some monomials of your own and find their products.
Solution:
The product of,some monomials is given below :
i) abc × a2bc = a3b2c2
ii) xy × x2z × yz2= x3y2z3
iii) p × q × r = p3q3r3
Question 1.
Complete the table:

Solution

Question 2.
Simplify: 4y(3y + 4)
Solution:
4y(3y + 4) = 4y × 3y + 4y × 4
= 12y2+ 6y
Question 3.
Simplify x(2x2- 7x + 3) and find the values of it for (i) x = 1 and (ii) x = 0
Solution:
x(2x2- 7x + 3)
= x × 2x2- x × 7x + x × 3
= 2x3- 7x2+ 3x
= 3 × 3 - 1 × 3 - 3 × 1 + 1 × 1
=9 - 3 - 3 + 1 = 4
∴(a - b)2= 4sq.units
[∵ (3 - 1)2= 22= 4]
(ii)
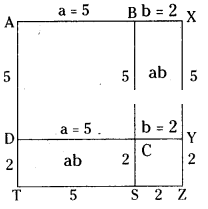
∴ (a - b)2= a2- 2ab + b2
Area of ABCD + Area of CYZS
= a2- 2ab + b2
area of ABCD - area of BXYC - area of DCST + area of CYZS
= 5 × 5 - 2 × 5 - 2 × 5 + 2 × 2
= 25 - 10 - 10 + 4
= 9 sq.units
[∵ (5 - 2)2= (3)2= 9]
Question 4.
Add the product: a(a - b), b(b - c), c(c - a)
Solution:
a(a - b) + b(b - c) + c(c - a)
=a × a - a × b + b × b - b × c + c × c - c × a
=a2- ab + b2- bc + c2- ca
=a2+ b2+ c2- ab - bc - ca
Question 5.
Add the product: x(x + y - r), y(x - y+r), z(x - y - z)
Solution:
x(x + y - r) +y(x - y + r) + z(x - y - z)
= x2 + xy - xr + xy - y2 + yr + zx - yz - z2
= x2 - y2 - z2 + 2xy - xr + yr + zx - yz
Question 6.
Subtract the product of 2x(5x - y) from product of 3x(x+2y)
Solution:
3x(x + 2y) - 2x(5x - y)
=(3x × x + 3x × 2y)-(2x × 5x - 2x × y)
= 3x2 + 6xy - (10x2 - 2xy)
= 3x2 + 6xy- 10x2 + 2xy
= 8xy - 7x2
Question 7.
Subtract 3k(5k - l + 3rn) from 6k(2k + 3l - 2rn)
Solution:
6k(2k + 3l - 2m) - 3k(5k - l + 3m)
= 12k2+ 18kl - 12km - 15k2 + 3kl - 9km
= -3k2 + 21kl - 21km
Question 8.
Simplify: a2(a - b + c) + b2(a + b - c) - c2(a - b - c)
Solution:
a2(a - b + c) + b2(a + b - c) - c2(a - b - c)
= a3 - a2b + a2c + ab2 + b3 - b2c - ac2 + bc2 + c3
= a3 + b3 + c3 - a2b + a2c + ab2 - b2c - ac2 - bc2
Question 1.
Multiply the binomials:
(i) 2a - 9 and 3a + 4
(ii) x - 2y and 2x - y
(iii) kl + lm and k - l
(iv) m2 - n2 and m + n
Solution:
i) 2a - 9 and 3a + 4
(2a - 9) (3a + 4) = 2a (3a + 4) - 9(3a + 4)
= 6a2 + 8a - 27a - 36
= 6a2 - 19a - 36
ii) x - 2y and 2x - y
(x - 2y) (2x - y) = x(2x - y) - 2y(2x - y)
= 2x2 - xy - 4xy + 2y2
= 2x2 - 5xy + 2y2
iii) kl + lm and k - l
(kl + lm) (k - l) = kl(k - l) + lm(k - l)
= k2l - l2k + klm - l2m
iv) m2 - n2 and m + n
(m2 - n2) (m + n) = m2(m + n) - n2(m + n)
= m3 + m2n - n2m - n3
Question 2.
Find the product:
(i) (x + y)(2x - 5y + 3xy)
(ii) (mn - kl + km) (kl - lm)
(iii) (a - 2b + 3c)(ab2 - a2b)
(iv) (p3 + q3)(p - 5q+6r)
Solution:
i) (x + y) (2x - 5y + 3xy)
= x(2x - 5y + 3xy) + y(2x - 5y + 3xy)
= 2x2 - 5xy + 3x2y + 2xy - 5y2 + 3xy2
= 2x2 - 5y2 - 3xy + 3x2y + 3xy2
ii) (mn - kl + km) (kl - lm)
= kl(mn - kl + km) - lm(mn - kl + km)
= klmn - k2l2 + k2lm - lm2n + kl2m - klm2
iii) (a - 2b + 3c) (ab2 - a2b) = a(ab2 - a2b) - 2b(ab2 - a2b) + 3c(ab2- a2b)
= a2b2 - a3b - 2ab3 + 2a2b2 + 3ab2c - 3a2bc
= 3a2b2 - a3b - 2ab3 + 3ab2c - 3a2bc
iv) (p3 + q3) (p - 5q + 6r) = p3(p - 5q + 6r) + q3(p - 5q + 6r)
= p4 - 5p3q + 6p3r + pq3 - 5q4 + 6rq3
= p4 - 5q4 - 5p3q + 6p3r + pq3 + 6rq3
Question 3.
Simplify the following:
(i) (x-2y) (y - 3x) + (x+y) (x-3y) - (y - 3x) (4x - 5y)
(ii) (m + n) (m2 - mn + n2)
(iii) (a - 2b + 5c) (a - b) - (a - b - c) (2a + 3c) + (6a + b) (2c - 3a - 5b)
(iv) (pq-qr-i-pr) (pq-i-qr) - (pr-i-pq) (p-i-q - r)
Solution:
i) (x - 2y) (y - 3x) + (x + y) (x - 3y) - (y - 3x) (4x - 5y)
= (y - 3x) [x - 2y - (4x - 5y)] + (x + y)(x - 3y)
= (y - 3x) [x - 2y - 4x + 5y] + (x + y) (x - 3y)
= (y - 3x) (3y - 3x) + (x + y) (x - 3y)
= y(3y - 3x) - 3x(3y - 3x) + x(x - 3y) + y(x - 3y)
= 3y2 - 3xy - 9xy + 9x2 + x2 - 3xy + xy - 3y2
= 10x2 - 14xy
ii) (m + n) (m2- mn + n2)
= m(m2 - mn + n2) + n(m2 - mn + n2)
= m3 - m2n + n2m + nm2 - mn2 + n3
= m3 + n3
iii) (a - 2b + 5c) (a - b) - (a - b - c) (2a + 3c) + (6a + b) (2c - 3a - 5b)
= a(a - 2b + 5c) - b(a - 2b + 5c) - 2a(a - b - c) - 3c(a - b - c) + 6a(2c - 3a - 5b) + b(2c - 3a - 5b)
= a2 - 2ab + 5ac - ab + 2b2 - 5bc - 2a2 + 2ab + 2ac - 3ac + 3bc + 3c2 + 12ac - 18a2 - 30ab + 2bc - 3ab - 5b2
= - 19a2 - 3b2 - 34ab + 16ac + 3c2
iv) (pq - qr + pr) (pq + qr) - (pr + pq) (p + q - r)
= pq(pq - qr + pr) + qr(pq - qr + pr) - pr(p + q - r) - pq(p + q - r)
= p2q2 - pq2r + p2qr + pq2r - q2r2 + pqr2 - p2r - pqr + pr2 - p2q - pq2 + pqr
= p2q2 - q2r2 + p2qr + pqr2 - p2r + pr2 - p2q - pq 2
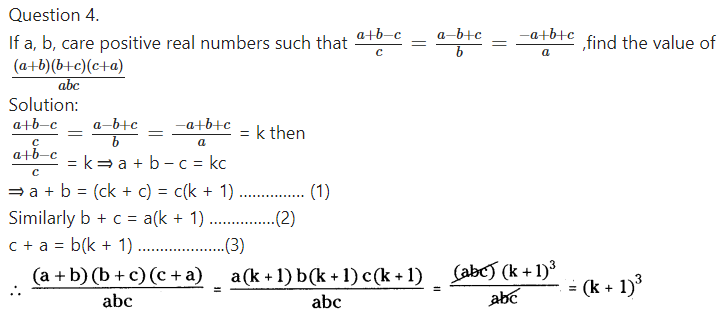
Question 1.
Select a suitable identity and find the following products
(i) (3k + 4l)(3k + 4l)
(ii) (ax2 + by2)(ax2 + by2)
(iii) (7d - 9e)(7d - 9e)
(iv) (m2 - n2)(m2 + n2)
(v) (3t + 9s) (3t - 9s)
(vi) (kl - mn) (kl + mn)
(vii) (6x + 5)(6x + 6)
(viii) (2b - a)(2b +c)
Solution:
(3k + 4l) (3k 4l) = (3k + 4l)2 is in the form of (a + b)2.
=(3k)2 + 2 × 3k × 4l+ (4l)2 [ (a+ b)2 = a2 + 2ab + b2
= 3k × 3k + 24kl + 4l × 4l
= 9k2 + 24kl + 16l2
ii) (ax2 + by2) (ax2 + by2) = (ax2 + by2)2 is in the form of (a + b)2.
= (ax2)2 + 2 × ax2 × by2 + (by2)2 [ ∵ (a + b)2 = a2 + 2ab + b2]
= ax2 × ax2 + 2abx2y2 + by2 × by2
= a2x4 + 2ab x2y2 + b2y4
iii) (7d - 9e) (7d - 9e)
= (7d - 9e)2 is in the form of (a - b)2.
= (7d)2 - 2 × 7d × 9e + (9e)2 [ ∵ (a - b)2 = a2 - 2ab + b2]
= 7d × 7d - 126de + 9e × 9e
= 49d2 - 126de + 81e2
iv) (m2 - n2) (m2 + n2) is in the form of (a + b) (a - b).
∴ (a + b) (a - b) = a2 - b2
∴ (m2 + n2) (m2 - n2) = (m2)2 - (n2)2 = m4 - n4
v) (3t + 9s) (3t - 9s) = (3t)2 - (9s)2 [ ∵ (a + b) (a - b) = a2 - b2 ]
= 3t × 3t - 9s × 9s
= 9t2 - 81s2
vi) (kl - mn) (kl + mn) = (kl)2 - (mn)2 [ ∵(a + b) (a - b) = a2 - b2 ]
= kl × kl - mn × mn
= k2l2 - m2n2
vii) (6x + 5) (6x + 6) is in the form of
(ax + b) (ax + c).
(ax + b) (ax + c) = a2x2 + ax(b + c) + bc
(6x + 5) (6x + 6) = (6)2x2 + 6x (5 + 6) + 5 × 6
= 36x2 + 6x × 11 + 30
= 36x2 + 66x + 30
viii) (2b - a) (2b + c) is in the form of (ax - b) (ax + c).
(ax - b) (ax + c) = a2x2 + ax(c - b) - cb
(2b - a) (2b + c) = (2)2(b)2 + 2b (c - a) - ca
= 4b2 + 2bc - 2ab - ca
Question 2.
Evaluate the following by using suitable identities:
(i) 3042
(ii) 5092
(iii) 9922
(iv) 7992
(v) 304 × 296
(vi) 83 × 77
(vii) 109 × 108
(viii) 204 × 206
Solution:
i) 3042 = (300 + 4)2 is in the form of (a + b)2.
∵ (a+b)2 = a2 + 2ab + b2
a = 300, b = 4
(300 + 4)2 = (300)2 + 2 × 300 × 4 + (4)2
= 300 × 300+ 2400 + 4 × 4
= 90,000 + 2400 + 16
= 92,416
ii) 5092 = (500 + 9)2
a = 500, b = 9
= (500)2 + 2 × 500 × 9 + (9)2
[ ∵ (a + b)2 = a2 + 2ab + b2]
= 500 × 500 + 9000 + 9 × 9
= 2,50,000 + 9000 + 81
= 2,59,081
iii) 9922 = (1000 - 8)2
a = 1000, b = 8
= (1000)2 - 2 × 1000 × 8 + (8)2 [∵ (a-b)2 = a2 - 2ab + b2]
= 1000 × 1000 - 16,000 + 8 × 8
= 10,00,000 - 16000 + 64
= 10,00,064 - 1600
= 9,98,464
iv) 7992 = (800 - 1)2
a = 800, b = 1
= (800)2 - 2 × 800 × 1 + (1)2
= 800 × 800 - 1600 + 1
= 6,40,000 - 1600 + 1
= 6,40,001 - 1600
= 6,38,401
v) 304 × 296 = (300 + 4) (300 - 4) is in the form of (a + b) (a - b).
(a + b) (a - b) = a2 - b2
∴ (300 + 4) (300 - 4) = (300)2 - (4)2
= 300 × 300 - 4 × 4
= 90,000 - 16
= 89,984
vi) 83 × 77 = (80 + 3) (80 - 3)
= (80)2 - (3)2 [ ∵ (a + b) (a - b) = a2 - b2]
= 80 × 80 - 3 × 3
= 6400 - 9
= 6391
vii) 109 × 108 = (100 + 9) (100 + 8)
= (100)2 + (9 + 8)100 + 9 × 8
= 10,000 + 1700 + 72
= 11,772
viii) 204 × 206 = (205 - 1) (205 + 1)
= (205)2 - (1)2 [∵ (a + b)(a-b) = a2 - b2]
= 205 × 205 - 1 × 1
= 42,025 -1
= 42,024
Question 1.
Verify the identity (a + b)2 ? a2 + 2ab + b2 geometrically by taking
(i) a = 2 units, b = 4 units
(ii) a = 3 units, b = 1 unit
(iii) a = 5 units, b = 2 unit
Solution:
(i)
= 4 × 4 + 4 × 2 + 2 × 2 + 4 × 2
= 16+ 8 + 4 + 8 = 36 sq.units
[∵ (2 + 4)2 = 62 = 36]
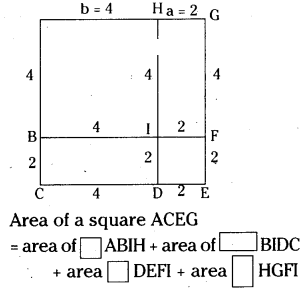
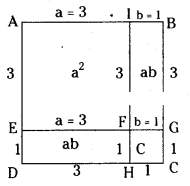
(ii)
Area of a square AEGI
= area of square ABCD + area of rectangle CDEF + area of square CFGH + area of rectangle BIHC.
= 3 × 3 + 3 × 1 + 1 × 1+3 × 1
= 9 + 3 + 1 + 3
= 16 sq. units
[∵ (3 + 1)2 = 42 = 16]
(iii)
= 5 × 5 + 2 × 5 + 2 × 2 + 5 × 2
= 25 + 10 + 4 + 10
= 49 sq.units
[∵ (5 + 2)2 = 72 = 49]
Question 2.
Verify the identity (a - b)2≡ a2 - 2ab+ b2 geometrically by taking
(i) a = 3 units, b= 1 unit
(ii) a = 5 units, b = 2 units
Solution:
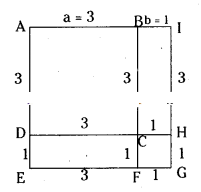
(i)
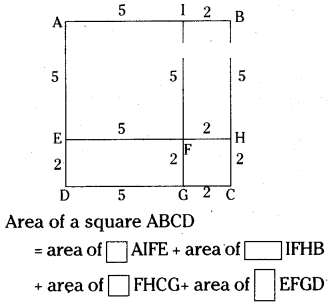
Area of AIFE + Area of FGCH = (a - b)2 = a2 - 2ab + b2 [area of AIFE - area of IBGF - area of EFHD + area of FGCH]
= 3 × 3 - 1 × 3 - 3 × 1 + 1 × 1
= 9 - 3 - 3 + 1 = 4
∴ (a - b)2 = 4 sq. units
[∵ (3 - 1 )2 = 22 = 4]
(ii)
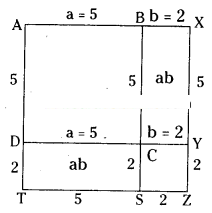
∴ (a - b)2 = a2 - 2ab + b2
Area of ABCD + Area of CYZS = a2 - 2ab + b2
area of ABCD - area of BXYC - area of DCST + area of CYZS
=5 × 5 - 2 × 5 - 2 × 5 + 2 × 2
= 25 - 10 - 10 + 4
= 9 sq.units
[∵ (5 - 2)2 = (3)2 = 9]
Question 3.
Verify the identity(a + b)(a - b) ≡ a2 - b2 geometrically by taking
(i) a = 3 units, b = 2 units
(ii) a = 2 units, b = 1 unit
Solution:
i)
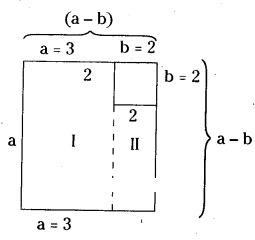
a2 - b2 = Area of Fig I. + Area of Fig II
= a(a - b) + b(a - b)
= (a - b) (a + b)
= 3 × 3 - 2 × 2
a2 - b2 = 9 - 4= 5sq . units
[ ∵ 32 - 22 = 9 - 4 = 5]
(ii)

a
2 - b
2 = Area of Fig I. + Area of Fig II
= a(a - b) + b(a - b)
= (a + b) (a - b)
=(2 + 1)(2 - 1)
= 3 × 1 = 3
a
2 - b
2 = 3 sq. units
[∵ (2
2 - 1
2) = 4 - 1 = 3]