9th Lesson Some Applications of Trigonometry Class 10 Important Questions with Solutions
10th Class Maths Some Applications of Trigonometry 1 Mark Important Questions
Question 1.
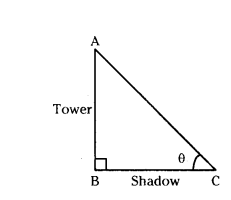
If the height of the tower is equal to the length of its shadow, then find the angle of elevation of the sun.
Solution:
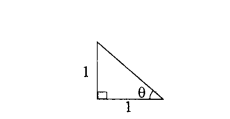
tan θ = 1
tan θ = tan 45°
θ = 45°
∴ Angle of elevation of sun = 45°.
Question 2.
What is the angle of elevation of the top of a 15 ih high tower at a point 15√3 in away from the base of the tower?
Solution:
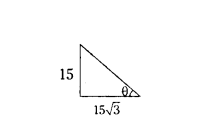
tanθ = 15/15√3 = 1/√3
tanθ = tan 30°
θ = 30°
∴ The angle of elevation = 30°
Question 3.
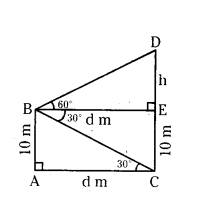
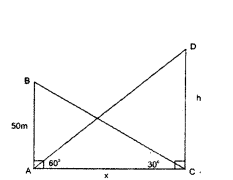
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60°. If the height of the tower is 20 m, find the distance of the point from the foot of the tower.
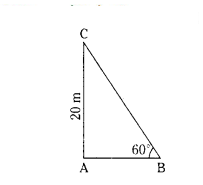
Solution:
tan 60° = 20/AB
√3 = 20/AB
AB = 20/√3 m.
Distance between foot of the tower and point is 20/√3 m.
Question 4.
The angle subtended by a vertical pole of height 100 m at a point on the ground 100√3 m from the base it has measure of
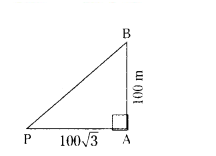
Solution:
tan P = 100/100√3
tan P = 1/√3
tan P = tan 30°
P = 30°
Question 5.
The string of a kite in air is 50 m long and it makes an angle of 60° with the horizontal. Assuming the string to be straight, find the height of the kite from the ground.
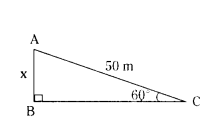
Solution:
sin 60° = x/50
√3/2 = x/50
√3 = x/50
x = 25√3 m
The height of kite from the ground = 25√3 m
Question 6.
What is the angle of elevation of the top of a 30 m high tower at a point 30 m away from the base of the tower ?
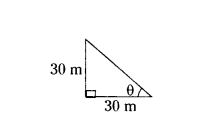
Solution:
tan θ = 30/30
tan θ = 1
tan θ = tan 45°
θ = 45°
∴ The angle of elevation = 45°
Question 7.
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground where it makes an angle 30°. The distance between the foot of the tree to the point where the top touches the ground is 8m. Find the height of the tree from where it is broken.
Solution:
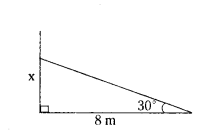
tan 30° = x/8
1/√3 = x/8
1/√3 = x/8
x = 8/√3 √3/√3 8√3/3 m
∴ Height of the tree from where it is broken = m
Question 8.
A tower stands vertically on the ground. From a point on the ground, which is 15 m away from the
foot of the tower, the angle of elevation of the top of the tower is found to be 60°. Find the height of the tower.
Solution:
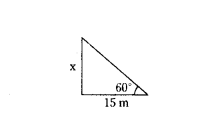
tan 60° = x/15
√3 = x/15
x = 15√3 m.
∴ Height of tower = 15√3 m
Question 9.
A pole 6 m high casts a shadow 2√3 m long on the ground, then find the angle of elevation of the sun.
Solution:
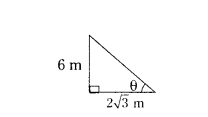
tan θ = 6/2√3 = 3/√3 = √3.√3/√3
tan θ = √3
tan θ = tan 60°
θ = 60°
∴ Angle of elevation = 60
Question 10.
In the figure θ = _________
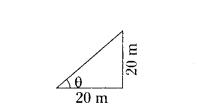
Solution:
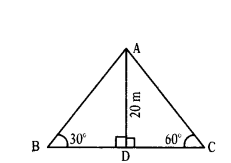
tan θ = 20/20
tan θ = 1
tan θ = tan 45°
θ = 45°
Question 11.
The ratio between the length of a pole and its shadow is 1 : 1 then find the angle of elevation of sun.
Solution:
tan θ = 1
tan θ = tan 45°
θ = 45°
Question 12.
The ratio between length of a tower and its shadow is √3 : 1 then find the angle of elevation of sun.
Solution:
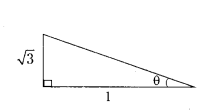
tan θ = √3/1
tan θ = √3
tan θ = tan 60°
θ = 60°
Question 13.
A pole of height 1 m make a shadow on the horizontal line √3 m, then find the sun’s altitude.
A) 30°
B) 45°
C) 60°
D) 75°
Solution:
A) 30°
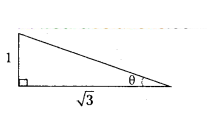
tan θ = 1/√3
tan θ = tan 30°
θ = 30°
Question 14.
From the figure, θ = .......
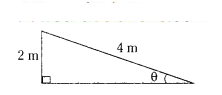
Solution:
sin θ = 2/4 = 1/2
sin θ = sin 30°
θ = 30°
Question 15.
In the figure x = ...... cm.
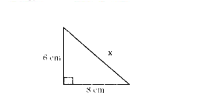
Solution:
x2 = 62 + 82
x2 = 100
x = 10 m
Question 16.
In the figure p = ....... cm.
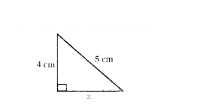
Solution:
x2 = 52 - 42 = 25 - 16 = 9
x = √9
x = 3 cm
Question 17.
In the figure AB ‖ CD, then θ = ........
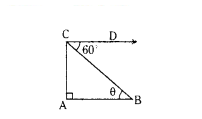
Solution:
60°
Question 18.
In the figure, MN ‖ AB then α = ......
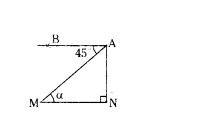
Solution:
45°
Question 19.
In the figure x = ...... cm
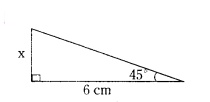
Solution:
tan 45° = x/6 ⇒ 1 = x/6 ⇒ x = 6cm
Question 20.
In the figure x = ...... cm
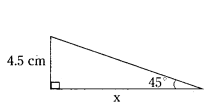
Solution:
tan 45° = 4.5/x ⇒ 1 = 4.5/x ⇒ x = 4.5cm
Question 21.
In the figure, AB = ....... cm.
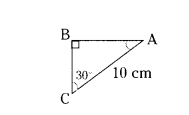
Solution:
sin 30°= AB/10
1/2 = AB/10
AB = 5 cm
Question 22.
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is ..... m.
Solution:
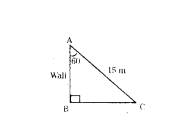
In ABC,
AB/AC = cos 60°
AB/15 = 1/2
AB = 15/2 m = 7.5m
Question 23.
Find the angle of elevation of the top of 10m a high tower at a point 10 m away from the base of the tower.
Solution:
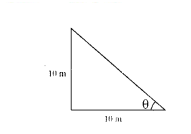
tan θ = 10/10
tan θ = 1
tan θ = tan 45°
θ = 45°
Required angle = 45°
Question 24.
In the figure AB ‖ CD then x = ....... cm.
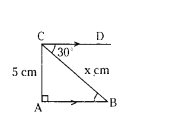
Solution:
∠ABC = ∠BCD = 30°
sin30° = 5/x
1/2 = 5/x
x = 5 × 2
x = 10
Question 25.
If a pole 6m high throws shadow of 2√3 m then the angle of elevation of the sun is ....... .
Solution:
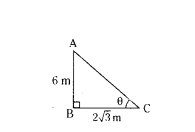
tan θ = 6/2√3
tan θ = 3/√3
tan θ = √3.√3/√3
tan θ = √3
tan θ = tan 60°
θ = 60°
Angle of elevation = 60°
Question 26.
In the figure x = ....... m.
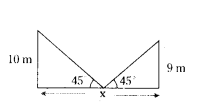
Solution:
x = 10 + 9 = 19 m
Question 27.
In the figure y = ......
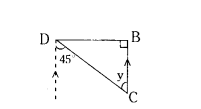
Solution:
∠BDC = ∠BCD, y = 45°
Question 28.
In the figure x = ......m.
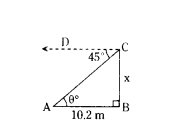
Solution:
θ = 45° (A.I.A)
tan 45° = x/10.2
1 = x/10.2
x = 10.2 m
Question 29.
Assertion (A) : In the figure θ = 60°
Reason (R) : In ∆ABC, if ∠B = 90° then ∠A + ∠C = 90°
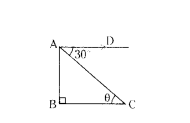
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A. A D
C) A is true, R is false.
D) A is false, R is true.
Solution:
D) A is false, R is true.
Question 30.
Assertion (A) : A pole is of height 6m makes same length of shadow on the ground then the sun’s angle of elevation is 45°.
Reason (R) : sin2θ + cos2θ = 1
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
Question 31.
Assertion (A) : In the figure x = 11 cm.
Reason (R) : cosec2θ - cot2θ = 1
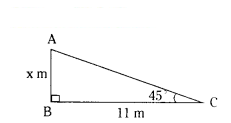
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
Question 32.
Assertion (A) : In the figure θ = 60°
Reason (R) : sec2θ - tan2θ = 1
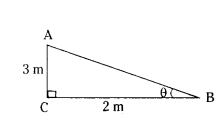
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
D) A is false, R is true.
Question 33.
Assertion (A) : The given figure represents sin example for angle of elevation.
Reason (R) : sinθ × cosecθ = -1.
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
C) A is true, R is false.
Question 34.
A tower of height 100 m casts a shadow of length 100√3 ni then what is the angle of elevation of the sun at that time ? (OR) In the given figure what is the value of angle θ?
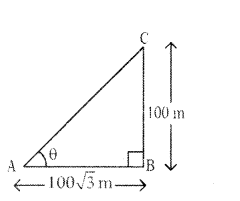
Solution:
In ∆ ABC
tan θ = BC/AB
tan θ = 100/100√3 = 2/√3
θ = 30°
Question 35.
Name the ‘angle of depression’ from the figure given below in which ∠B = 90°.
Solution:
∠DAC
Question 36.
Sathwik is flying a kite with the support of string of length 100 m. which make an angle (If the string is tied) 60° with the ground, then height of the kite is ________
Solution:
50√3 m (or) 86.6 m.
Question 37.
At a particular time, if the angle of elevation of the sun is 45°, then the length of the shadow of a 5 m high tree is __________ .
A) 5√3 m
B) 10 m
C) 5 m
D) 5/√3
Solution:
C) 5 m
Question 38.
Draw a rough diagram to the given situation.
"A person observed a top of a tree 10 m. away from its foot at the angle of elevation is 45°."
Solution:
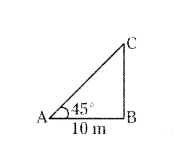
BC = Height of the tree.
Question 39.
Identify the angle of depression from the below figure.
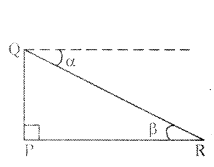
Solution:
α
Question 40.
Draw a rough diagram to the following situation. "A person is flying a kite at an angle of elevation θ and the length of thread from his hand to kite is l."
Solution:
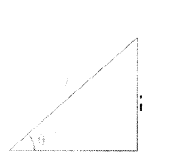
Question 41.
"You are observing top of your school building at an angle of elevation 60° from a point which is at 20 metres distance from foot of the building". Draw a rough diagram to the above situation.
Solution:
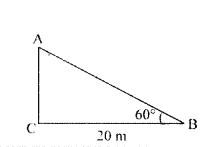
Question 42.
Draw the diagram for the following situations. Length of the shadow of a x meter high pole is y meter in the morning 7 o’ clock and the angle of elevation of the sunrays with the ground is ‘θ’.
Solution:
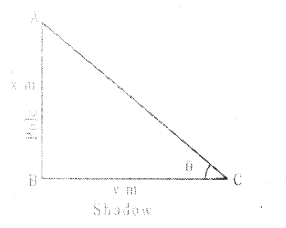
Question 43.
The given figure shows the observation of point ‘C’ from point A. Find the angle of depression from A.
Solution:
30°
Question 44.
Statement (A): If the length of shadow of a vertical pole is equal to its height, then the angle of elevation of the sun is 45°.
Statement (B) : According to pythagoras theorem, h2 = l2 + b2, where h = hypotenuse, l = Length and b = base.
i) Both A and B are true
ii) A is true, B is false
iii) A is false, B is true
iv) Both A and B are false
Solution:
i) Both A and B are true
Question 45.
From a window, ‘h’ m high above the ground, of a house in a street, the angles of elevation and depression of the top and bottom of another house on the opposite side of the street are α and β respectively, then match the column.
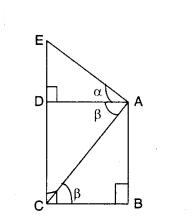
A) DB
B) DE
C) CE
D) AD
i) h(1 +tan α cot β)
ii) h sin β
iii) h tan α cot β
iv) h cot β
Answer:
A - (iv), B - (iii), C - (i), D (ii)
Question 46.
Jani observes Vanaja on the ground from the balcony of the first floor of a building at an angle of depression 60°. The height of the first floor of the building is 10 metres. Draw the diagram for this data.
Answer:
AB = Height of the first floor
Question 47.
Draw the diagram for the following situations. Length of the shadow of a x meter high pole is y meter in the morning 7 o’ clock and the angle of elevation of the sunrays with the ground is ‘θ’.
Answer:
10th Class Maths Some Applications of Trigonometry 2 Mark Important Questions
Question 1.
The angle of elevation of the top of a tower from a point on the ground which is 30 m away from the foot of the tower is 30°. Find the height of the tower.
Solution:
Let A be the point of observer, B be the foot of the tower and C be the top of the tower.
Angle of elevation ∠CAB = 30°
Let height of tower BC = h m
Distance between observer and foot of the tower AB = 30 m
In ∆ABC, ∠B = 90°
tan ∠CAB = Opposite side/Adjacent side = AB/AC
tan 30° = h/30
1/√3 = h/30
h = 30/√3 × √3/√3 = 30√3/3 = 10√3
Therefore, height of the tower BC = 10√3 m
Question 2.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole if the angle made by the rope with the ground level is 30°.
Solution:
Let AB be the height of pole = h m
AC be the length of rope = 20 m
Angle of elevation ∠ACB = 30°
In ∆ABC, ∠B = 90°
sin ∠ACB = Opposite side/Hypotenuse = AB/AC
sin 30° = h/20 (∵ sin 30° = 1/2)
1/2 = h/20 ⇒ h = 1/2 × 20 = 10 m
Therefore, height of pole AB = 10 m
Question 3.
A bridge across a river makes an angle of 45° with the river bank. If the length of the bridge across the river is 150 m. What is the width of the river ?
Solution:
Let PQ be the length of bridge = 150 m
QR is the width of the river = x m
Angle of elevation ∠QPR = 45°
In ∆PQR, ∠R = 90°
sin ∠QPR = Opposite side/Hypotenuse = QR/PQ
sin 45° = x/150
1/ √2= x/150
x = 150/√2 √2/√2 = 150√2/2 = 75√2 m
Therefore, width of the river QR = 7√2 m
Question 4.
The height of tower is 20 m. What is the length of its shadow when sun’s altitude is 45° ?
Solution:
Let length of the tower AB = 20 m
Let length of the shadow BC = x units
Angle of elevation ∠ACB = θ = 45°
In ∆ABC, ∠B = 90°
tan ∠ACB = Opposite side/Adjacent = AB/BC
tan 45° = 20/x
1 = 20/x (∵ tan 45° = 1)
∴ x = 20 m
Therefore, length of shadow BC = 20 m.
Question 5.
If the ratio of the height of tower and the length of the shadow is √3 : 1. What is the angle of elevation of the sun ?
Solution:
Given ratio of the height of tower and its shadow = AB = BC = √3 : 1
i.e., AB/BC = √/1
In ∆ABC,
∠B = 90°
tan θ = Opposite side/Adjacent = AB/BC
tan θ = √3/1 = √3 = tan 60°
∴ θ = 60° (∵ AB/BC = √3/1)
Therefore, angle of elevation = 60°
Question 6.
What is the angle of elevation of the sun when the length of the shadow of a vertical pole is equal to its height ?
Solution:
Given height of pole = Length of its shadow
Angle of elevation = θ
In ∆PQR, ∠Q = 90°
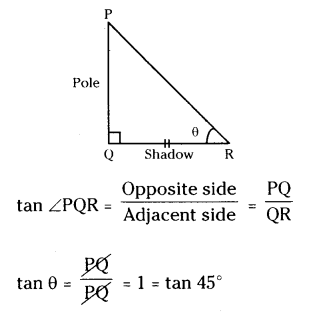
θ = 45° (∵ tan 45° = 1)
Therefore, angle of elevation = 45°.
Question 7.
Find the length of the shadow on the ground of a pole of height 18 m when angle of elevation θ of the sun is such that tan θ = 6/7.
Solution:
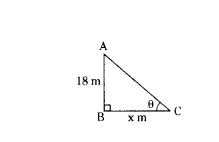
Given tan θ = 6/7
18/x = 6/7
6x = 18 × 7
x = 18×7/6
x = 3 × 7
x = 21 m
∴ The length of shadow = 21 m.
Question 8.
The angle of depression of a car parked on the road from the top of 150 m high tower is 30°. Find the distance of the car from the tower (in metres).
Solution:
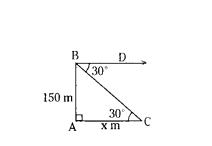
Let AB is the height of the tower
Given angle of depression = 30°
In the figure
∠DBC = ∠ACB = 30° (A.I.A)
AC = x m
AB = 150 m 150
tan 30° = 150/x
1/√3 = 150/x
x = 150√3 m
∴ Distance of the car from the tower = 150√3m.
Question 9.
From the top of a pole, the angle of elevation of the top of other pole is found to be equal to the angle of depression of the foot of the tower. First pole is of height 20 m. Find the distance between the two poles.
Solution:
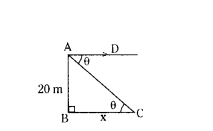
In the figure, θ = 45°
tan θ = 20/x
tan 20/x
1 = 20/x
x = 20 m
∴ Distance between two poles = 20m.
Question 10.
A tower of height 60 m, casts a shadows 20√3 m long on the ground, then what is the angle of elevation of the sun ?
Solution:
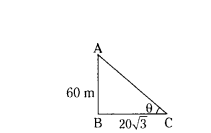
Let AB = 60 m
BC = 20√3 m.
tan θ = 60/20√3 = 3/√3
tan = tan 60° ⇒ θ = 60°
Question 11.
A boy observed the top of an electric pole at an angle of elevation of 30°, when the observation point is 10 meters away from the foot of the pole. Draw suitable diagram for the above situation.
Solution:
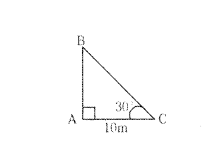
AB = Height of the Electric Pole
AC = Distance between the foot of the pole to the observer = 10 m
Angle of Elevation = 30°
Question 12.
A flag pole 4 m tall casts a 6 m shadow. At the same time, a nearby building casts a shadow of 24. m. How tall is the building?
Solution:
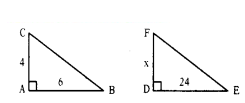
4/x = 6/24
6x = 24 × 4 ⇒ x = 24×4/6 = 16 m.
∴ The height of the building = 16 cm.
Question 13.
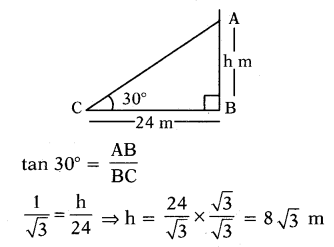
Rehman observed the top of a temple at an angle of elevation of 30°, when the observation point is 24 m. away from the foot of the temple. Find the height of the temple.
Solution:
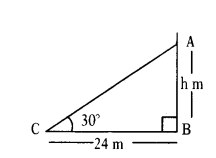
In ∆ABC
tan 30° = AB/AC
1/√3 = h/30
⇒ h = 24/√3 × √3/√3 = 8√3 m
Question 14.
A flag pole 7 m tall, casts a 8 m shadow. At the same time, a nearby building casts a shadow of 32 mts. How tall is the building ?
Solution:
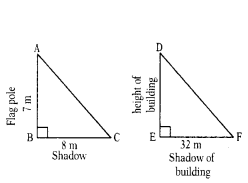
∆ABC ~ ∆DEF
AB/DE = BC/EF ⇒ = 8/32
∴ DE = 28 m
Question 15.
A person from the top of a building of height 25 m has observed another building top and bottom at an angle of elevation 45° and at an angle of depression 60° respectively. Draw a diagram for this data.
Solution:
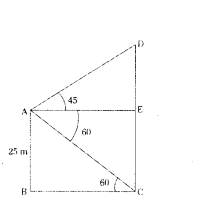
Question 16.
A person observed the top of a tree at an angle of elevation of 60° when the observation point was 5 m away from the foot of the tree. Draw a diagram for this data.
Solution:
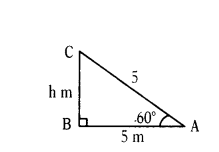
From the figure,
BC = height of the tree = h m.
‘A’ is the observation point.
AB = Distance between tree to the observation point.
Angle of elevation is 60°.
Question 17.
If the angle of elevation of sun increases from ‘O’ to 90 then the length of shadow of a tower decreases. Is this true ? Justify your answer.
Solution:
Yes, this statement is true.
We observe this in day to day life.
AD - ground, BC - lower, AB - shadow.
Question 18.
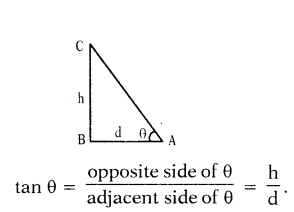
If a tower of height ’h’ is observed from a point with a distance’d’ and angle ‘θ’, then express the relation among h, d and θ.
Solution:
For writing relation between h, θ, d as tan θ = h/d
Question 19.
"The top of a tower is observed at an angle of elevation 45° and the foot of the tower is at a distance of 30 metres from the observer". Draw a suitable diagram for this data.
Solution:
C - Point of observer
AB - Tower
A - Top of the tower
Question 20.
"An observer standing at a distance of 10m from the foot of a tower, observes its top with an angle of elevation of 60°." Draw a suitable diagram for this situation.
Solution:
AB - Tower
C - Position of observer
60° - Angle of elevation
Question 21.
A boat has to cross a river. It crosses river by making an angle of 60° with bank, due to the stream of river it travels a distance of 450 m to reach another side of river. Draw a diagram to this data.
Solution:
AB - width of river
AD, BC are river banks
AC - The distance travelled in river = 450 m
A - initial point, C - terminal point
Question 22.
A person 25 mts away from a cell - tower observes the top of cell - tower at an angle of elevation 30°. Draw the suitable diagram for this situation.
Solution:
AB = cell tower
BC = distance between
observer and cell tower
Question 23.
A straight highway leads to foot of the tower. A man standing at the top of the tower observes a car at an angle of depression of θ, which is approaching the foot of the tower with a uniform speed. Six seconds later the angle of depression is ?. Draw a diagram for this data and analyze.
Solution:
Question 24.
From the top of a tower of h m height, Anusha observes the angles of depression of two points X and Y on the same side of tower on the ground to be α and β. Draw the suitable figure for the given information.
Solution:
Question 25.
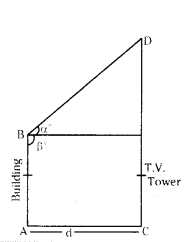
From the top of the building, the angle of elevation of the top of a T.V. tower is α° and the angle of depression to its (T.V. tower) foot is β°. If distance of the building from the tower is ‘d’ meters, draw the suitable diagram to the given data.
Answer:
Question 26.
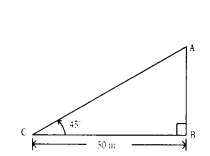
The angle of elevation of the top of a tower from a point on the ground, which is 50 m away from the foot of the tower is 45°. Draw the diagram for the situation.
Answer:
10th Class Maths Some Applications of Trigonometry 4 Mark Important Questions
Question 1.
The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60 m. Find the height of the first tower.
Solution:
Let AB be the height of first tower and
CD be the height of second tower.
Let BE = x m
AB = AE + BE = (60 + x) m
CD = AE = 60 m
Distance between two towers = AC = DE = 140 m
Angle of elevation at the top of the first tower ∠BDE = 30°
In ∆BDE, ∠BED = 90°
tan ∠BDE = Opposite side/Adjacent side = AB/AC
tan 30° = x/140
1/√3 = x/140
x = 140/√3 m
Height of the first tower = AE + BE = 60 + x
Therefore, height of the first tower = (60 + 140/√3)m
Question 2.
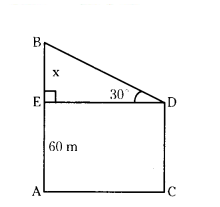
The length of a string between a kite and a point on the ground is 90 m. If the string makes θ with the ground level such that tan θ = 15/8, how high is the kite ? Assume that there is no slack in the string.
Solution:
Let point of kite A and point of kite on the ground B, other end of the string C.
Length of string and point in the ground BC = 90 m
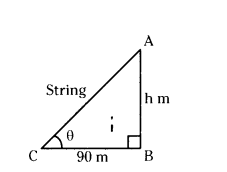
Let height of kite AB = h m
Angle of elevation ∠ACB = θ
and tan θ = 15/8
In ∆ABC, ∠B = 90°
tan ∠ACB = Opposite side/Adjacent side
tan θ = AB/BC
15/8 = h/90
⇒ h = 15/8 90
= 675/4 = 168.75 m
Therefore, height of the kite is 168.75 m.
Question 3.
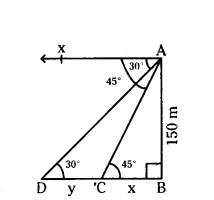
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then the width of the river.
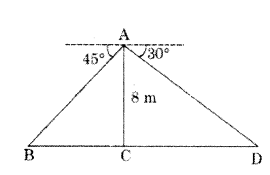
Solution:
Let AC is the height of the bridge.
AC = 8m
given angles of depression = 30C and 45°
AC ⊥ BD
In the figure.
∠EAB = ∠ABC = 45° = 0 (AIA)
∠FAD = ∠ADC = 30° = α (AIA)
tan θ = 8/x
tan 45° = 8/x
1 = 8/x
x = 8 ..... (1)
tan 30° = 8/y
1/√3 = 8/y
y = 8√3 ...... (2)
(1) + (2) ⇒ x + y = 8 + 8√3 = 8(1 + √3) m
∴ Width of the river = 8(1 + √3) m.
Question 4.
Two poles of heights 25 m and 35 m stand vertically on the ground. The tops of two poles are connected by wire, which is inclined to the horizontal at an angle of 30°. Find the length of the wire and the distance between the poles.
Solution:
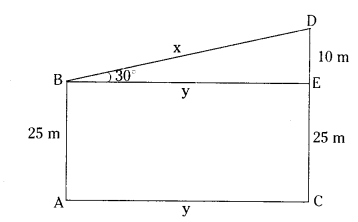
In the figure
AB = height of first pole = 25 m
CD = height of second pole = 35 m
Let the length o| wire = x m
Distance between poles = y m
Let BE = AC = y m
CE = AB = 25 m.
DE = 35 - 25 = 10 m.
In Right triangle BDE
tan 30° = 10/y
1/√3 = 10/y
y = 10√3 m
sin 30° = 10/x
1/2 = 10/x
x = 20m
∴ Length of the wire = 20 m
Distance between poles = 10√3 m .
Question 5.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. (Use √3 = 1.73)
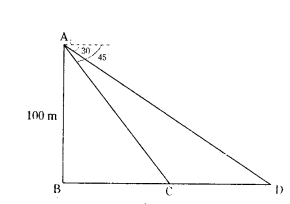
Solution:
In the figure
AB = 100 m
BC = x m
CD = y m
∠EAD = ∠BDA = 30° (AIA)
∠EAC = ∠BCA = 45° (AIA)
In Right triangle, ABC
tan 45° = 100/x
1 = 100°/x
x = 100m
In ∆ABD, tan 30° = 100/x+y
2/√3 = 100/x+y
100√3 = 100 + y
100√3 - 100 = y
y = 100(√3 - 1)m
Distance travelled = 100 (√3 - 1)
= 100(1.732 - 1)
= 100 (0.732)
= 73.2 m
Question 6.
At a point of level ground, the angle of elevation of a vertical tower is, found to be a such that tan α = 1/3. After walking 100 m towards the tower, the angle of elevation p becomes such that tan β = 3/4. Find the height of the tower.
Solution:
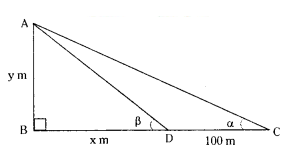
In the figure CD = 100 m
AB y m = Height of tower
BD = x m
Let ∠ACD = α, ∠ADB = β.
tan α = y/x+100
1/3 = y/x+100
x + 100 = 3y
x - 3y = -100 .... (1)
tan β = y/x
3/4 = y/x
3x = 4y
3x - 4y = 0 ..... (2)
y = 60 m
3x - 4(60) = 0
3x = 240
x = 80 m
∴ Height of the Tower = 80 m
Question 7.
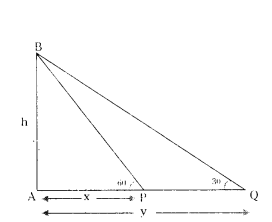
In Figure, the angles of elevation of the top of a tower AB of height ‘h’m, from two points P and Q at a distance of x m and y m from the base of the tower respectively and in the same straight line with it, are 60° and 30°, respectively. Prove that h2 = xy.
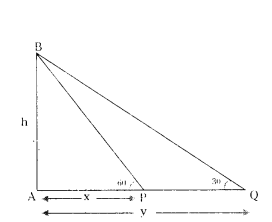
Solution:
In right triangle BAP
tan 60° = h/x
√3 = h/x
h = √3x .... (1)
In ∆ABQ,
tan 30° = h/y
1/√3 = h/y
h√3 = y
h = y/√3 .... (2)
(1) × (3) ⇒ h . h = √3x.y/√3
h2 = xy
Question 8.
Two poles of equal heights are standing opposite each other on either side of the road of with 60 m. From a point P between them on the road, the angles of elevation of the top of the poles are 60° and 30° respectively, as shown in Figure, Find the height of the poles and distances of the point from the poles.
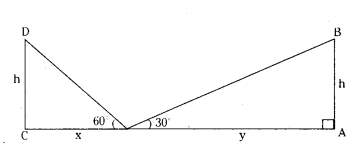
Solution:
In the figure
tan 60° = h/x
√3 = h/x
h = √3x ..... (1)
tan 30° = h/y
1/√3 = h/y
h = y/√3 ..... (2)
(1) = (2)
y/√3 = √3x
y = 3x ....
In the figure AC = 60 m
x + y = 60
y = 60 - x ...... (4)
∴ 60 - x = 3x (by (3))
60 = 3x + x
60 = 4x
x = 60/4
x = 15 m
y = 60 - 15 = 45 m. (by (4))
y = 45 m
h = √3x (by (1))
h = √3 × 15 m
h = 15√3 m
∴ Height of poles = 15√3 m
Distance from poles = 15 m (or) 45 m
Question 9.
An observer of height 1.6 m is 11.2 m away from a palm tree. The angle of elevation of the top of tree from his eyes is 45°. What is the height of the palm tree ?
Solution:
Height of observer = 1.6 m = AB = DE
Distance from palm tree = 11.2 m = AE = BD
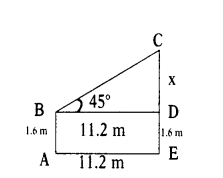
Angle of elevation = ∠CBD = 45°
In ∆ BCD = tan 45° = CD/BD
⇒ 1 = CD/11.2 ⇒ CD = 11.2 m
∴ Height of palm tree = CE = CD + DE = 11.2 m + 1.6 m = 12.8 m.
Question 10.
Two poles of heights 6 m. and 11m. stand on a plane ground. If the distance between the feet of the poles is 12 m. find the distance between their tops.
Solution:
Given,
Height of first pole = AB = 6m.
Height of second pole = CD = 11 m
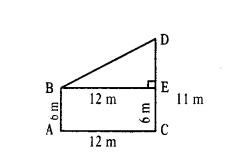
Distance between feet of poles = AC = 12 m
Distance between the tops of the pole, i.e., BD
So, BE = AC = 12 m
Similarly, AB = EC = 6m.
Now, DE = DC - EC = 11 - 6 = 5 m
BD2 = DE2 + BE2
= 52 + 122 - 25 + 144 = 169
∴ BD - 13 m
Question 11.
Suppose Siddu is shooting an arrow from the top of a building at an height of 6 m to a target on the ground at an angle of depression of 60°. What is the distance between Siddu and the object?
Solution:

∴ Distance = 4√3 m or 4 × 1.732 = 6.928 m.
Question 12.
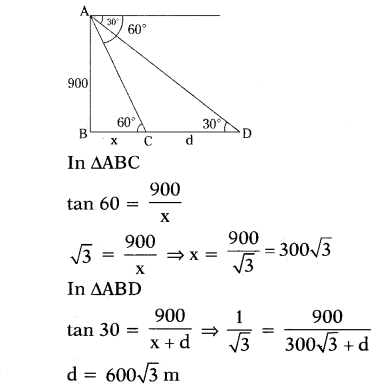
An observer flying in an aeroplane at an altitude of 900 m observes two ships in front of him, which are in the same direction at an angles of depression of 60° and 30° respectively. Find the distance between the two ships.
Solution:
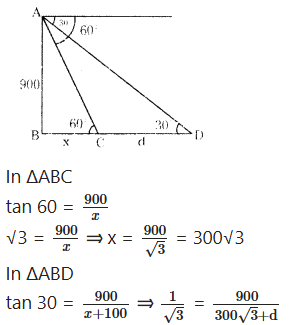
d = 600√3 m
Question 13.
From the top of the building the angle of elevation of the top of the cell tower is 60° and the angle of depression to its foot is 45°, if the distance of the building from the tower is 30 meters, draw the suitable diagram to the given data.
Solution:
AB - Height of the building
CD - Height of the tower C
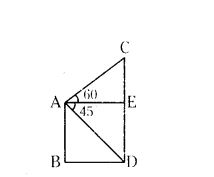
∠CAE - angle of eleva-tion = 60°
∠EAD - angle ol depres-sion = 45°
Distance between building and tower = BD = 30m
Question 14.
If two persons standing on either side of a tower of height 100 metres observes the top of it with angles of elevation of 60° and 45° respectively, then find the distance between the two persons. [Note: Consider the two persons and the tower are onvthe same line.]
Solution:
Tower height = 100 m
Angles of elevation = 60° and 45°
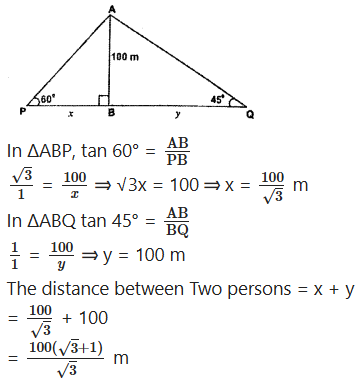
Question 15.
An observer flying in an aeroplane at an altitude of 900 m observes two ships in front of him, which are in the same direction at an angles of depression of 60° and 30° respectively. Find the distance between the two ships.
Solution:
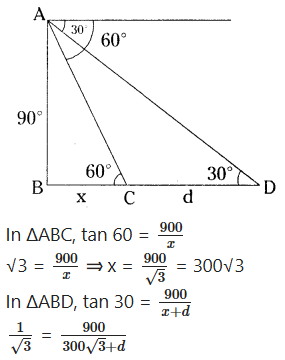
d = 600√3 m
Question 16.
Two poles are standing opposite to each other on the either side of the road which is 90 feet wide. The angle of elevation from bottom of first pole to top of second pole is 45°, the angle of elevation from bottom of second pole to top of first pole is 30°. Find the . heights of poles, (use √3 = 1.732).
Solution:
Let AB = x and CD = y
In ∆ ABD, tan 30° = x/90
x = 90 × tan 30°
⇒ x = 90 × 1/√3 = 90√3/√3×√3 = 30√3
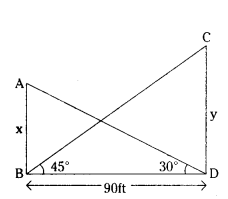
= 30(1.732) = 51.960 = 51.96 ft.
In ∆ BDC, tan 45° = y/90
⇒ y = 90 × tan 45°
⇒ y = 90 × 1 ⇒ y = 90 ft
∴ Height of the first pole = 51.96 ft
Height of the second pole = 90ft
Question 17.
The angle of elevation of the top of a tower from two points at a distance of 4m and 9 m from the base of the tower and in the same straight line with it, are complementary. Prove that the height of the tower is 6 m.
Solution:
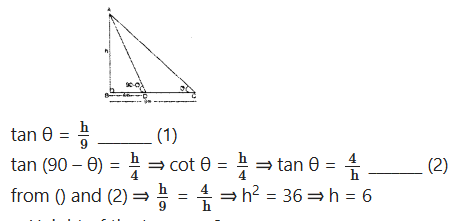
∴ Height of the tower = 6m
10th Class Maths Some Applications of Trigonometry 8 Mark Important Questions
Question 1.
An electrician has to repair an electric fault on a pole of height 4 m. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which when inclined at an angle of 60° to the horizontal would enable him to reach the required position ?
Solution:
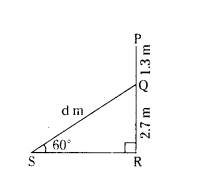
Let P and R are the top and foot of the pole.
Let Q be the point 1.3 m below the top P of the pole PR.
Then QR = PR - PQ = 4 - 1.3 = 2.7 m
Length of the ladder = QS = d m
Angle of elevation at Q = ∠QSR = 60°
In ∆QRS, ∠R = 90°
Sin ∠QSR = Opposite side/Hypotenuse
Sin 60° = QR/QS
√3/2 = 2.7/d
√3 d = 2.7 × 2
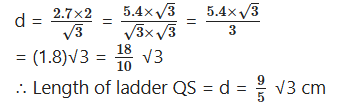
Question 2.
From a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30°. The angle of elevation of the top of a water tank is 45°. Find 0 height of the tower ii) the depth of the tank.
Solution:
i) Let A be the point on the ground 40 m away from the foot of the tower B.
Let C be the top of the tower.
Let BC = h m.
CD be the height of the tank = x m. Angle of the elevation at C = ∠CAB = 30° Angle of the elevation at D = ∠DAB = 45°
In ∆ ABC, ∠B = 90°
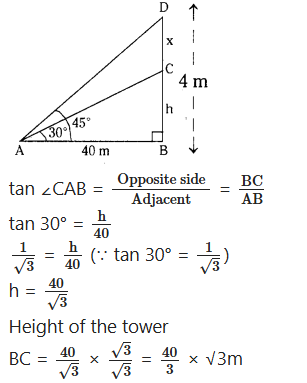
ii) In ∆ABD, ∠B = 90°, ∠DAB = 45°
tan ∠DAB = BD/AB = BC+CD/AB
tan 45° = h+x/40
1 = h+x/40 (∵ tan 45° = 1)
h + x = 40
x = 40 - h
= 40 - 40√3/3
= 40(1 - √3/3)
∴ Depth of the tank = CD = x = 40(3-√3/3)m.
Question 3.
The angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
Solution:
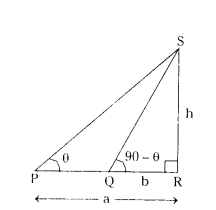
Let P and Q are two points on the ground.
R be the foot of the tower.
S be the top of the tower.
From P angle of elevation at the top of towers ∠SPR = θ.
From Q angle of the elevation at the top of tower ∠SQR = 90 - θ
PR = a metres
QR = b metres
In ∆PRS, ∠SPR = θ.
tan∠SPR = SR/PR
tan θ = h/a → (1)
In ∆QRS, ∠SQR = 90 - θ
tan ∠SQR = SR/PR
tan(90 - θ) = SR/PR (∵ tan (90 - θ) = cot θ
cot θ = h/b → (2)
From (1) and (2)
tan θ.cot θ = h/a . h/b
1 = h2/ab (∵ tan θ.cot θ = 1)
h2 = ab
∴ Height of the tower = h = √ab m
Question 4.
A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. It is takes 12 minutes for the angle of depression to change from 30° to 45°. How soon after this, will the car reach the tower ?
Solution:
Let A and B are the two positions of car. C and D are the foot of the tower and top of the tower.
Time taken to move d distance = 12 minutes
Let height of the tower CD = h m
Let AB = d m, BC = x m
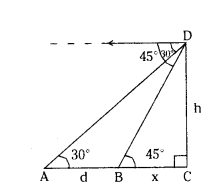
Angle of elevation at the top of tower from A = ∠DAC = 30°
Angle of elevation at the top of tower from B = ∠DBC = 45°
In ∆DAC, ∠DAC = 30°
tan∠DAC = Opposite side/Adjacent side = CD/AC
tan 30° = CD/AB+BC
1/√3 = h/d+x(∵ tan 30° = 1/√3)
h = d+x/√3 → (1)
In ∆DBC, ∠DBC = 45°
tan ∠DBC = CD/AC
tan 45° = h/x (∵ tan 45° = 1)
1 = h/x
h = x → (2)
From (1) and (2)
d+x/√3 = x
d + x = x√3
d = x√3 - x
d = x (√3 - 1) m
Time taken to travel d = x (√3 - 1) metres is 12 minutes.
Time taken to travel x metres
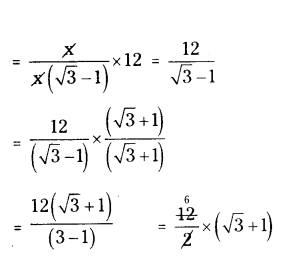
∴ Time taken to reach the tower = 6(√3 + 1) minutes
Question 5.
Two pillars of equal height and on either side of a road, which is 100 m wide. The angles of elevation of the top of the pillars are 60° and 30° at a point on the road between the pillars. Find the position of the point between the pillars and the height of each pillar.
Solution:
Let A and B are the top and foot of the first pillar.
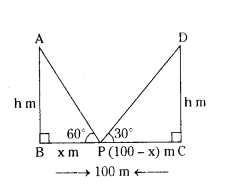
C and D are the foot and top of the second pillar.
Let height of the pillars AB = CD = h m. Let point of observer is P.
Let distance from the foot of the first pillar to the observer = BP = x m.
Distance between two pillars BC = 100 m.
Then distance from the foot of the second pillar to the observer = CP = BC - BP = (100 - x) m
Angle of elevation from P at A is ∠APB = 60°
Angie of elevation from P at B is ∠DPC = 30°
In ∆ABP, ∠B = 90°
tan∠APB = Opposite side/Adjacent side = AB/BP
tan 60° = h/x (∵ tan 60° = √3)
√3 = h/x
h = x.√3 m → (1)
In ∆DCP, C = 90°
tan∠DPC = CD/PC
tan 30° = h/100?x
1/√3 = h/100-x(∵ tan 30° = 1/√3)
h = 100-x/√3 → (2)
From (1) and (2)
x√3 = 100-x/√3
x√3.√3 = 100 - x
3x + x = 100
4x = 100
x = 100/4 = 25 m 4
BP = 25 m,
PC - 100 - x = 100 - 25 = 75 m
So, observer is 25 m far from the first pillar.
Question 6.
An aeroplane when flying at a height of 4000 m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the aeroplane at that instant.
Solution:
Let the positions of aeroplanes are A and B.
Point of plane on the ground C.
Let point of observer is P.
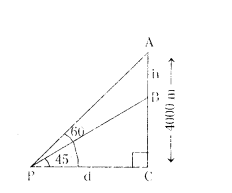
Height of the first plane AC = 4000 m
Distance between the two planes = AB = h m
then height of the second plane = BC = AC - AB = (4000 - h) m
Let distance between observer and plane on the ground = PC = d m.
Angle of elevation at first plane = ∠APC = 60°
Angle of elevation at second plane = ∠BPC - 45°
In ∆APC, ∠C = 90°
tan∠APC = Opposite side/Adjacent side = AC/PC
tan 60° = 4000/d
√3 = 4000/d ⇒ √3d = 4000
d = 4000/√3 → (1)
In ∆BPC, ∠C = 90°
tan∠BPC = 4000?h/d
tan 45° = 4000?h/d
1 = 4000?h/d ⇒ d = 4000 - h → (2)
From (1) and (2)
4000/√3 = 4000 - h
h + 4000/√3 = 4000
h = 4000 - 4000/√3
= 4000(1 - 1/√3)
Distance between two planes = h = 4000(√3-1/√3) m
Question 7.
The horizontal distance between two poles is 15 m. The angle of depression of the top of the first pole as seen from the top of the second pole Is 30°. If the height of the second pole is 24 m. Find the height of the first pole.
Solution:
Let A and B are top and foots of first pole.
C and D are the foot and tops of second pole.
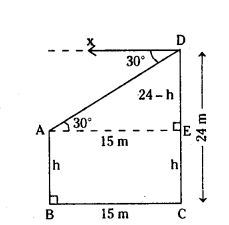
Let height of first pole AB = CE = h m
Height of second pole CD = 24 m
Then DE = CD - CE = (24 - h) m.
Distance between two poles = BC = AE = 15 m
Angle of depression at the top of the first pole ∠XDA = ∠DAE = 30°
In ∆DAE, ∠E = 90°
tan∠DAE = Opposite side/Adjacent side = DE/AE
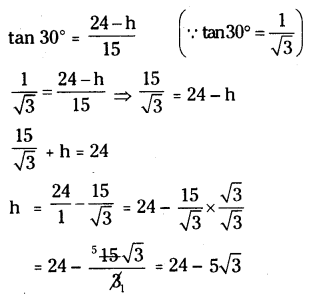
= 24 - 5(1.732) = 24 - 8.66
∴ Height of first pole = 15.34 m.
Question 8.
An aeroplane at an altitude of 1200 m find that two ships are sailing towards it in the same direction. The angles of depression of the ships as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two ships.
Solution:
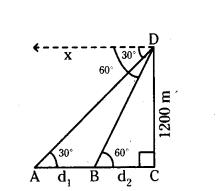
Let A and B are the places of two ships and C be the place aeroplane on the ground and D be the place of plane.
Height of aeroplane CD = 1200 m.
Let distance between two ships A and B is AB = d1 m.
Let BC = d2 m.
Angle of depression at ship A is ∠DAC = ∠XDA = 30°
Angle of depression at ship B is ∠DBC = ∠XDB = 60°
In ∆DBC, ∠C = 90°
tan∠DBC = Opposite side/Adjacent side = CD/BC
tan 60° = 120/d2 (∵ tan 60° = √3)
√3 = 120/d2
d2 = 1200/√3 = 1200×√3/√3×√3 = 1200√3/3
d2 = 400√3 m → (1)
In ∆ACD, ∠C = 90°
tan∠DAC = CD/AC
tan 30° = 1200/d1+d2 (∵ tan 30° = 1/√3)
1/√3 = 1200/d1+d2
d1 + d2 = 1200√3
d1 = 1200 √3 - d2 (∵ d2 = 400√3)
= 1200 √3 - 400 √3
d1 = 800 √3
Therefore, distance between the two ships = 800 √3 m (or) 800 × 1.732 = 1385.6 m
Question 9.
A man standing on the dock of a ship, which is 10 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
Solution:
Let foot of the ship A point of man on the ship is B. Foot of the hill C and top of the hill D.
Height of the ship AB = CE = 10 m
Let CD = h m
Height of hill CD = CE + DE = (10 + h) m
Let distance between hill from the ship = AC = BE = d m
Angle of elevation at the top of hill ∠EBD = 60°
Angle of depression at the foot of the hill.
∠ACB = ∠CBE = 30°
In ∆ACB, ∠A = 90°
tan∠ACB = Opposite side/Adjacent side = AB/AC
tan 30° = 10/d
1/√3 = 10/d (∵ tan 30° = 1/√3)
d = 10√3 m
In ∆BDE, ∠E = 90°
tan∠DBE = DE/BE
tan 60° = h/d (∵ tan 60° = √3)
√3 = h/d
h = √3 d = √3(10√3) (∵ d = 10√3)
h = √3 × √3 × 10 = 3 × 10 = 30 m
Therefore, height of the hill = CD = h + CE = 30 + 10 = 40 m
Distance between hill and the ship = 10√3 m (or) 10 (1.732) = 17.32 m.
Question 10.
As observed from the top of a 150 m tall lighthouse the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find distance between the two ships.
Solution:
Let top of the light house A, and foot B. Points of first ship C and second ship D.
Height of light house AB = 150 m
Let the distance between light house and first ship BC = x m
Let the distance between two ships CD = y m
Angle of depression at first ship ∠XAC = ∠ACB = 45°
Angle of depression at second ship ∠XAD = ∠ADB = 30°
In ∆ACB, ∠B = 90°
tan∠ACB = Opposite side/Adjacent side = AB/BC
tan 45° = 150/x
1 = 150/x (∵ tan 45° = 1)
∴ x = 150 m
In ∆ABD, ∠B = 90°
tan∠ACB = AB/BD
tan 30° = 150/BC+CD
1/√3 = 150/x+y
x + y = 150 (∵ tan 45° = 1)
150 + y = 150 √3 (∵ x = 150)
y = 150 √3 - 150
y = 150 (√3 - 1) = 150 (1.732 - 1)
= 150 (0.732)
y = 109.5 m
Therefore distance between two ships
= 109.5 m
Question 11.
A person from the top of a building of height 15 meters observes the top and the bottom (foot) of a cell tower with the angle of elevation as 60° and the angle of depression as 45° respectively. Then find the height of that cell tower.
Solution:
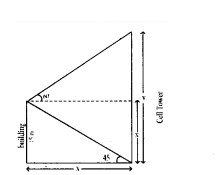
Angle of elevation of the top of the tower = 60°.
Angle of depression to the foot of the tower = 45°.
Height of the building = 15 m.
Distance between tower and building = x m
Let, height of the tower = y m
From the figure
tan 45° = 15/x ⇒ 1 = 15/x ⇒ x = 15 m
Also tan 60° = y?x/15 ⇒ √3 = y?15/15 ⇒ 15√3 = y - 15
⇒ y = 15 + 15√3 = 15(√3 + 1)
= 15(1.732 +1)
= 15 × 2.732 = 40.98 m.
Question 12.
From the top of a tower of 50 m high, Neha observes the angles of depression of the top and foot of another building to be 45° and 60° respectively. Find the height of the building.
Solution:
Let CD = height of the building = h
AB = height of the tower = 50 m
BD = EC = distance between tower and building = d m
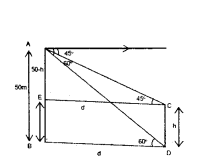
tan 45° = 50?h/d ⇒ 1 = 50?h/d
⇒ d = 50 - h _____ (1)
tan 60° = 50/d ⇒ √3 = 50 d ⇒ 50/√3
50/√3 50 - h (∵ From (1))
50 = 50√3 - h√3
h√3 = 50√3 - 50
h = 50√3-50/√3 = 50√3-1/√3 m
Question 13.
The angle of elevation of the top of a hill from the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If the tower high. Find the height of the hill.
Solution:
Given height of the tower =AB = 50 m
Let height of hill be CD = h m
and distance between their feet be AC = x m
∠ACB = 30°, ∠CAD = 60°
From right angled ∆ ABC, tan 30° = AB/AC
1/3 = 50/x
∴ x = 50√3 m.
From right angled ∆ ACD, tan 60° = CD/AC
√3 = h/x
h = x√3 m
h = 50√3.√3 (∵ x = 50√3 m)
h = 50 × 3 ⇒ h = 150 m.
Question 14.
Two boys on either side of their school building of 20 m height observes its top at the angles of elevation 30° and 60° respectively. Find the distance between two boys.
Solution:
Let BC = Distance between two boys
AD = Height of the school building = 20 m
From ∆ABD,
cot 30° = BD/AD ⇒ √3 = BD/15
BD = 20√3 m.
From ∆ACD,
cot 60° = DC/AD
1/√3 = DC/20 ⇒ DC = 20/√3 m
∴ BC = BD + DC
= 20√3 + 20/√3 = 80/√3 m
Question 15.
A man observes top of a tower at an angle of elevation of 30°. When he walked 40 m towards the tower, the angle of elevation is changed to 60°. Find the height of the tower and distance from the first observation point to the tower.
Solution:
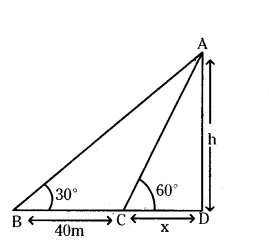
Given height of the tower we will find
BC = 40 m; CD = x m
Height of the tower = h m
From figure tan 30° = h/x+40
1/√ = h/x+40
x + 40 = √3h ⇒ x = √3h - 40 ____ (1)
tan 60°= h/√3h-40 ∵ from(1)]
3h - 40√3 = h
2h = 40√3 ⇒ h = 20√3 m
∴ Height of the tower = 20√3 m.
x = √3h - 40 = √3 × 20√3 - 40
= 3 × 20 - 40
= 60 - 40 = 20 m
Distance from the first observation point to the tower.
BD = x + 40 = 20 + 40 = 60m.
Question 16.
A wire of length 24 m had been tied with electric pole at an angle of elevation 30° with the ground. As it is covering a long distance, it was cut and tied at angle of elevation 60° with the ground. How much length of the wire was cut ?
Solution:
Let AD be length of wire before cut = 24 m
Let AG be length of wire after cut (AC) = x m
Height of the electric pole = AB
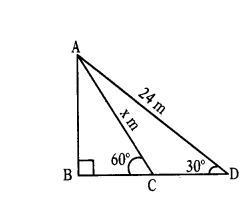
Angle of elevation
∠BDA = 30°
∠BCA = 60°
In right ∆le ABD
sin 30° = AB/AD
1/2 = AB/24 ⇒ 2AB = 24 ⇒ AB = 12 m
In right ∆le ABC
sin 60° = AB/AC ⇒ √3/2 = 12/AC
⇒ √3 AC = 24 ⇒ AC = 24/√3
= 8√3 m = 8 × 1.732 = 13.856
Length of the wire was cut = 24 - 13.856 = 10.144 m
Question 17.
A man on the top of vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 seconds to change the angle of depression from 30° to 60°, then how long will the car take to reach the tower from that point.
Solution:
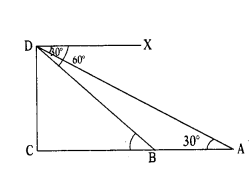
Position of observer = ‘D’
Initial position of car = ‘A’
then angle of depression = ∠XDA = 30°
∴ In ∆ACD, ∠C = 30°
⇒ tan 30 = CD/AC = 1/√3
⇒ CD = AC/√2 ______ (1)
and after 12 seconds of time, position of car = ‘B’
then angle of depression = ∠XDB = 60° = ∠DBC
∴ In ∆BCD, ∠B = 60°
⇒ tan 60° = CD/BC = √3
⇒ CD = BC√3 ______ (2)
∴ (1) = (2)
⇒ CD = AC/√2 = BC√3 ⇒ AC = 3BC
Now from the figure
AC = AB + BC
⇒ 3BC = AB + BC (∵ AC = 3BC)
⇒ AB = 2BC
So the time taken to cover the distance AB or the distance 2BC = 12 seconds
∴ Time taken to cover BC = 6 sec (∵ 12/2)
Then the time taken to approach the tower = time taken to cover the distance
AC = 3BC = 3(6) = 18 seconds
that means it takes 6 more seconds (18 - 12) to reach tower.
Question 18.
Two boys on either side of a temple of 60 m height observe its top at the angles of elevation 60° and 30°. Find the distance between the two boys.
Solution:
Height of the temple BD = 60 metres.
Angle of elevation of one person ∠BAD = 60°
Angle of elevation of another person ∠BCD = 30°
Let the distance between the first person and the temple, AD = x and distance between the second person and the temple, CD = d
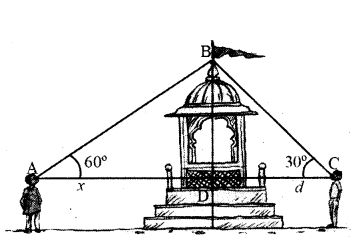
From ∆BAD
tan 60° = BD/AB
√3 = 60/x
x = 60/√3 .... (1)
From ∆BCD
tan 30° = BD/d
1/√3 = 60/d
d = 60√3 .... (2)
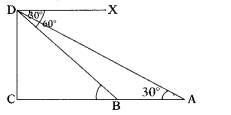
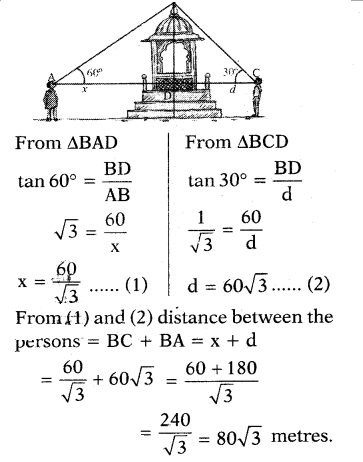
From (1) and (2) distance between the persons = BC + BA = x + d
= 60/√3 + 60√3 = 60+180/√3
= 240/√3 = 80√3 meters.
Question 1.
A boy observed the top of an electric pole at an angle of elevation of 30°, when the observation point is 10 meters away from the foot of the pole. Draw suitable diagram for the above situation.
Solution:
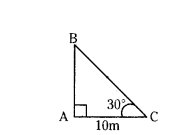
AB = Height of the Electric Pole
AC = Distance between the foot of the pole to the observer = 10 m
Angle of Elevation = 30°
Question 2.
Draw a diagram to find the height of the kite in the situation given below. "A person is flying a kite at an angle of elevation ‘a’ and the length of thread from his hand to kite is ‘l".
Solution:
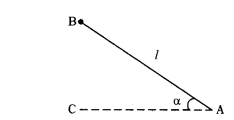
B is position of kite.
AB = Length of thread = ‘l’
Persons hand is at ‘A’.
∠BAC - α - Angle of elevation.
Question 3.
A flag pole 4 m tall casts a 6 in shadow. At the same time, a nearby building casts a shadow of 24. m. How tall is the building?
Solution:
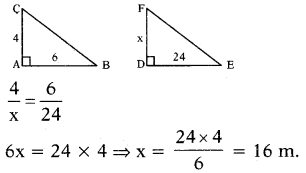
∴ The height of the building = 16 cm.
Question 4.
A tower is 100√3 m high.Find the angle of elevation of its top when observed from a point 100 m away from the foot of the tower.
Solution:
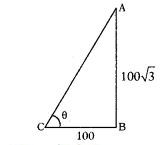
Height of a tower
(AB) = 100√3 m.
Distance between foot of tower and observer point (BC) = 100m
In∆ABCTan θ = 100√3/100 = √3 = tan 60°
∴ θ = 60°
Question 5.
Rehman observed the top of a temple at an angle of elevation of 30°, when the observation point is 24 m. away from the foot of the temple. Find the height of the temple.
Solution:
In∆ABC,
Question 6.
A flag pole 7 m tall, casts a 8 m shadow. At the same time, a nearby building casts a shadow of 32 mts. How tall is the building?
Solution:
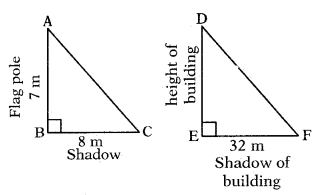
∆ABC ~ ∆DEF;
AB/DE = BC/EF ⇒ 7/DE = 8/32
∴ DE = 28 m
Question 7.
An observer of height 1.8 m is 13.2 in away from a palm tree. The angle of elevation of the top of tree from his eyes is 45°. What is the height of the palm tree?
Solution:
Height of observer = 1.8 m = AB
Distance from palm tree = 13.2 m = AE = BD
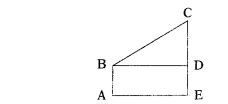
Angle of elevation = ∠CBD = 45°
In ∆ BCD = tan 45° = CD/BD
⇒ 1 = CD/13.2 ⇒ CD = 13.2 m
∴ Height of palm tree = CE
= CD + DE
= 13.2 m + 1.8 = 15 m.
Question 8.
Two poles of heights 6 m. and 11m. stand on a plane ground. If the dis¬tance between the feet of the poles is 12 m. find the distance between their tops.
Solution:
Given,
Height of first pole = AB = 6 m.
Height of second pole = CD = 11 m
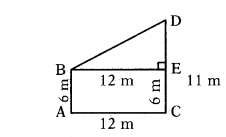
Distance between feet of poles = AC = 12 m
Distance between the tops of the pole,
i.e., BD
So, BE = AC = 12 m ’
Similarly, AB EC 6m.
Now, DE = DC - EC = 11 - 6 - 5 m
BD2 = DE2 + BE2
= 52 + 122 = 25 + 144 - 169
∴ BD = 13 m
Question 9.
An observer flying in an aeroplane at an altitude of 900 m observes two ships in front of him, which are in the same direction at an angles of depression of 60° and 30° respectively. Find the distance between the two ships.
Solution:
Question 10.
A wire of length 24 m had been tied with electric pole at an angle of elevation 30° with the ground. As it is covering a long distance, it was cut and tied at angle of elevation 60° with the ground. How much length of the wire was cut?
Solution:
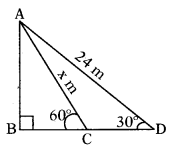
Let AD be length of wire before cut = 24 m
Let AC be length of wire after cut (AC) = x m
Height of the electric pole = AB
Angle of elevation
∠BDA = 30°
∠BCA = 60°
In right ∆le ABD
sin 30° = AB/AD
1/2 = AB/24 ⇒ 2AB = 24 ⇒ AB = 12m
In right ∆le ABC
sin 60° = AB/AC ⇒ √3/2 = 12/AC
= √3 AC = 24 ⇒ AC = 24/√3
= 8√3m = 8 × 1.732 = 13.856 m
Length of the wire was cut
= 24 - 13.856 = 10.144 m
Question 11.
A man on the top of vertical tower observes a car moving at a uniform speed coming direcdy towards it. If it takes 12 seconds to change the angle of depression from 30° to 60°, then how long will the car take to reach the tower from that point.
Solution:
Position of observer = ‘D’
Initial position of car = ‘A’
then angle of depression
= ∠DA = 30°
∴ In ∆ACD, ∠C = 30°
⇒ tan 30 = CD/AC = 1/√3
⇒ CD = AC/√3 .......(1)
and after 12 seconds of time, position of car = ’B’
then angle of depression
= ∠XDB = 60° = ∠DBC
∴ In ∆BCD, ∠B = 60°
⇒ tan 60° = CD/BC = √3
⇒ CD = BC√3 ...... (2)
∴ (1) = (2)
⇒ CD = AC/√3 = BC √3 ⇒ AC = 3BC
Now from the figure
AC = AB + BC
⇒ 3BC = AB + BC ( ∵ AC = 3BC)
⇒ AB = 2BC
So the time taken to cover the distance
AB or the distance 2BC = 12 seconds
∴ Time taken to cover BC distance
= 6 sec (∵ 12/2)
Then the time taken to approach the tower = time taken to cover the distance
AC = 3BC = 3(6) = 18 seconds that means it takes 6 more seconds (18 - 12) to reach tower.
Question 12.
Two boys on either side of a temple of 60 m height observe its top at the angles of elevation 60° and 30°. Find the distance between the two boys.
Solution:
Height of the temple BD = 60 metres.
Angle of elevation of one person ∠BAD = 60° .
Angle of elevation of another person ∠BCD = 30°
Let the distance between the first person and the temple, AD = x and distance between the second person and the temple, CD = d
Question 13.
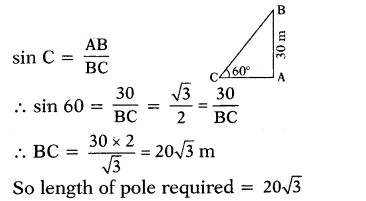
A pole is arranged from a height of 30m from the ground, making 60° angle with earth. Then what is its length?
Solution:
Height from the earth = AB = 30m
Length of pole = BC = ?
∠ACB = 60°
Then in ∆ABC AB BC
Question 14.
A long pole is broken in a storm. Top end of the broken pole touched the head of a man at a distance of ‘d Then find the angle between the man and the pole that before storm.
Solution:
AB - height of pole
AC - distance = d
CD = man
‘D’ is head of man
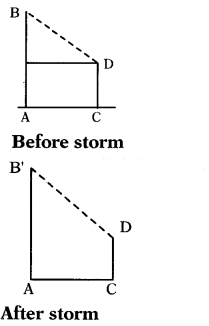
After storm
B’ - broken point
‘D’= ‘B’ (∵ they coincides after storm because D’ i.e., head of man which is touched by end of tree = B’)
∴ AngIe between these two points = zero.
Question 15.
A kite is flown from a building with a height (h) m with a long rope. Now the kite and the person having it are observed with angles of elevation α and β respectively by a boy. The distance between boy and building is ‘x’ m. So draw a diagram for this data.
Solution:
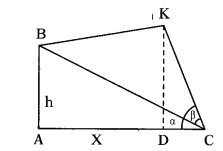
AB is building height = h
K is kites position.
‘C’ is position of boy.
AC = Distance between boy and building AB = X
∠DCK = Elevation angle to kite = ∝
∠BCK Elevation angle to building top = β
Question 16.
A person observes tops of two buildings with an angle of elevations 35° and 46° from the mid point in between them. So which building is higher ? Why?
Solution:
Let ‘E’ is mid point between two buildings AB and CD.
In ∆AEB let ∠E = 35°
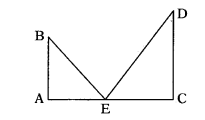
tan 35 = AB/AE
∴ Height of building (AB)
= (AE) tan 35° ...... (1)
In ∆ECD let ∠E - 46°
∴ tan 46 = CD/EC
∴ Height of building (CD)
= EC tan 46° ...... (2)
In (1) and (2) AE = EC
( ∵ E is mid point)
Then value of tan 35 is less than tan 46°. So, height of CD (= EC tan 46) is higher than height of AB (= EC tan 35)
(∵ tan 46 > tan 35)
(∵ values of tan increases from 0 to 90)
Question 17.
A 15m long pole forms 53 m long shadow at 8 AM in the morning. Then find the angle made by sun rays with earth.
Solution:
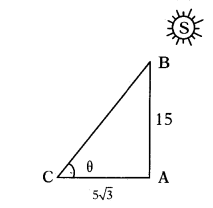
As shown in figure
Height of pole (AB) = 15m
Length of shadow (BC) = 5√3
∠ACB = θ
∴ In ∆ABC tan θ = AB/AC= 15/5√3 = √3
∴ tan θ = √3 ⇒ θ = 60°
∴ The sun rays made 60° angle on the earth at that time.
Question 18.
A right circular cylindrical tower, height ‘h’ and radius ‘r’ stands on the ground. Let ‘P’ be a point in the horizontal plane ground and ABC be the semi-circular edge of the top of the tower such that B is the point in it nearest to P. The angles of elevation of the points A and B are 45° and 60°
respectively. Show that h/r = √3(1+√5)/2
Solution:
As shown in the figure
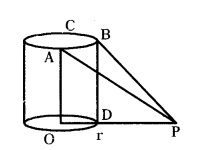
OA = BD = h (height of cylinder)
OD = r (radius of cylinder) .
‘O’ is the centre.
ABC is the edge of semicircle (in the top of cylinder).
B is nearer to the point P. So B should be at the outer edge of diameter. That means just above ‘D’.
∠DPB = 60°, ∠OPA = 45° (given)
In ∆BDP tan P = BD/DP (P = 60°, BD = h)
⇒ √3 = h/DP ⇒ h = DP√3 ......(1)
In ∆AB tan P = OA/OP
(here P = 45°, OA = h)
⇒ tan 45° = OA/OP = 1
⇒ OA = OP
So OA = h = OP = OD + DP = r + DP
So h = r + DP ....... (2)
From the equation (1) & (2)
h = DP√3 , h = r + DP
∴ DP√3 = r + DP
So r = DP√3 - DP
r = DP (√3 - 1) ...... (3)
