6th Lesson Triangles Class 10 Important Questions with Solutions
10th Class Maths Triangles 1 Mark Important Questions
Question 1.
Write the properties of similar triangles.
Answer:
Two triangles are said to be similar, if their
- corresponding angles are equal.
- corresponding sides are proportional.
Question 2.
Write the examples of similar figures.
Answer:
All circles, all squares, all equilateral triangles, etc.
Question 3.
State the Thales theorem.
Answer:
If a line drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.
Question 4.
State the converse of basic proportionality theorem.
Answer:
If a line divides any two sides of a tri¬angle in the same ratio, then the line must be parallel to the third side.
Question 5.
State the pythagoras theorem.
Answer:
In a right angled triangle square of the hypotenuse is equal to the sum of the squares of the other two sides.
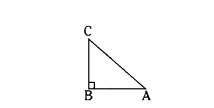 That is in ΔABC, ∠B = 90° then AC2 = AB2 + BC2.
That is in ΔABC, ∠B = 90° then AC2 = AB2 + BC2.
Question 6.
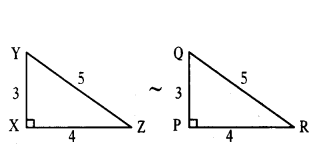
In ΔABC and ΔDEF, AB/DE = BC/FD. Which of the following makes the two triangles similar ?
A) ∠A = ∠D
B) ∠B = ∠D
C) ∠B = ∠E
D) ∠A = ∠F
Solution:
B) ∠B = ∠D
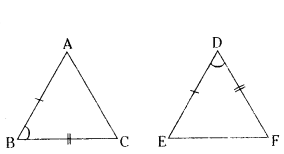
AB/DE = BC/FD
∴ ∠B = ∠D
ΔABC ~ ΔEDF
Question 7.
In the given fig. DE ‖ BC. Find BC.
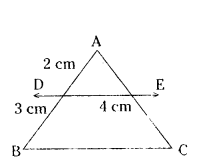
Solution:
AD/AB = DE/BC
2/2+3 = 4/BC
2/5 = 4/BC
2BC = 20
BC = 10 cm.
Question 8.
In ΔABC, PQ ‖ BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.
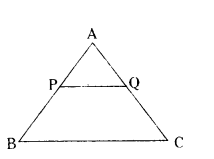
Solution:
PQ ‖ BC
By BPT
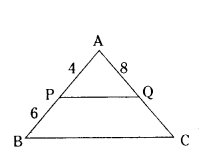
4/6 = 8/QC
2/3 = 8/QC
2QC = 24
QC = 12
AC = 8 + 12 = 20 cm
Question 9.
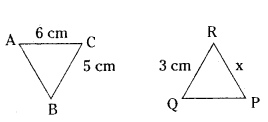
In the given figure, ΔABC ~ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; then the value of x is :
Solution:
ΔABC ~ ΔQPR
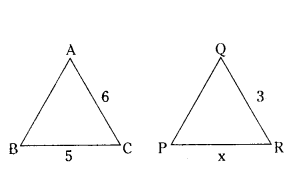
6/3 = 5/2
2 = 5/x
x = 5/x = 2.5 cm
Question 10.
If in ΔABC and ΔPQR, AB/QR = BC/PR = CA/PQ then :
A) ΔPQR ~ ΔCAB
B) ΔPQR ~ ΔABC
A) ΔCBA ~ ΔPQR
B) ΔBCA ~ ΔPQR
Solution:
A) ΔPQR ~ ΔCAB
 ΔPQR ~ ΔCAB
ΔPQR ~ ΔCAB
Question 11.
Which of the following is not a similarity criterion of triangle ?
A) AA
B) SAS
C) AAA
D) RHS
Answer:
D) RHS
Question 12.
If ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm, then ∠B = ..... .
Solution:
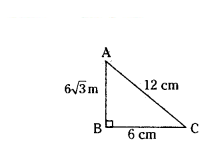
AB2 = (6√3)2 = 36 × 3 = 108
AC2 = 122 - 144
BC2 = 62 = 36
AC2 = AB2 + BC2
144 = 108 + 36
144 = 144
∠B = 90°
Question 13.
In the given fig. DE ‖ BC. Which of the following is true ?
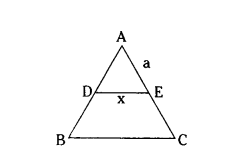
A) x = a+b/ay
B) y = ax/a+b
C) x = ay/a+b
D) x/y = a/b
Solution:
C) x = ay/a+b
DE ‖ BC, ΔADE ~ ΔABC
a/x = a+b/y
x(a + b) = ay
x = ay/a+b
Question 14.
In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = 1/2 DE then the two triangles are
A) congruent, but not similar not congruent
B) similar, but not congruent
C) neither congruent nor similar
D) congruent as well as similar
Solution:
B) similar, but not congruent
AB = 1/2 DE
2AB = DE
ΔABC ~ ΔDEF but not congruent.
Question 15.
In the given fig. If DE ‖ BC. Find EC.
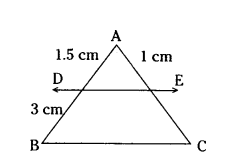
DE ‖ BC
AD/DB = AE/EC
1.5/3 = 1/EC
EC = 2 cm
Question 16.
In the given figure, AD = 2 cm, DB = 3 cm, DE = 2.5 cm and DE ‖ BC. Find the value of x.
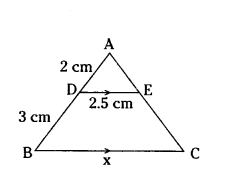
Solution:
ΔADE ~ ΔABC
AD/DB = DE/x
2/5 = 2.5/x
2x = 2.5 × 5
x = 2.5 × 5/2
x = 2.5 × 2.5
x = 6.25 cm
Question 17.
In two triangles ΔPQR and ΔABC, it is given that AB/BC = PQ/PR For these two triangles to be similar, which of the following should be true ?
A) ∠A = ∠P
B) ∠B = ∠Q
C) ∠B = ∠P
D) ∠A = ∠R
Solution:
C) ∠B = ∠P
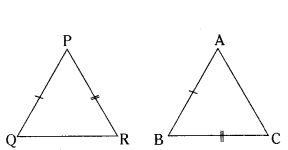
AB/BC = PQ/PR
AB/PQ = BC/PR
ΔPQR ~ ΔBAC
∠P = ∠B.
Question 18.
In ΔABC, DE ‖ BC, AD = 4 cm, BD = 6 cm and AE = 5 cm, find the length of EC.
Solution:
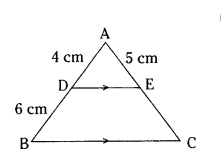
DE ‖ BC
By BPT
4/6 = 5/EC
2/3 = 5/EC
EC = 15/2 = 7.5 cm
Question 19.
In ΔABC, DE ‖ BC, AD = 2 cm, BD = 3 cm, DE: BC is equal to ...... .
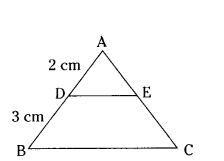
Solution:
DE ‖ BC, ΔADE, ΔBC
∠ A = ∠A (Common angle)
∠D = ∠B (Corresponding angle) by AA Similarity
ΔADE ~ ΔABC
AD/AB = AE/AC = DE/BC
2/2+3 = DE/BC
2/5 = DE/BC
DE : BC = 2 : 5
Question 20.
In the given fig. DE ‖ BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then find the length of AE.
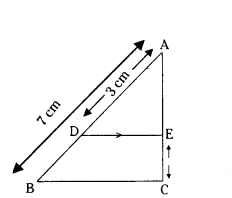
DE ‖ BC, BD = 7 - 3 = 4 cm
By BPT 3/4 = AE/3
4AE = 9
AE = 9/4
AE = 2.25 cm.
Question 21.
The perimeters of two similar triangles are 24 cm and 18 cm respectively. If one side of the first triangle is 8 cm then what is the corresponding side of second triangle ?
Answer:
6
Question 22.
In ΔABC, ∠B = 90°, BD ⊥ AC.
If AD = 8 cm and BD = 4 cm, then what is the length of CD ?
Answer:
2 cm.
Question 23.
Among "Circles", "Squares" and "Triangles", which are always similar ?
Answer:
Circles and squares are always similar.
Question 24.
In ΔABC and ΔDEF,
if ∠B = ∠E, ∠C = ∠F, then which of the following is a true statement ?
A) AB/DE = CA/EF
B) BC/EF = AB/FD
C) AB/DE = BC/EF
D) CA/FD = AB/EF
Answer:
C) AB/DE = BC/EF
Question 25.
Given DE ‖ BC, AD = 4.5 cm, BD = 9 cm, and EC = 8 cm. What is the length of AE?
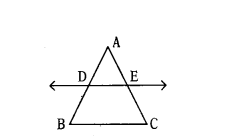
Solution:
AD = 4.5 cm, BD = 9 cm, EC = 8 cm
AD/DB = AE/EC ⇒ 4.5/9 = AE/8 ⇒ 9AE = 36
∴ AE = 4 cm
Question 26.
The sides of two equilateral triangles ABC and DEF are 4 cm. and 5 cm. respeclively. Find ar(△DEF)/ar(△ABC).
Solution:
Ratio of areas of Δ = (Ratio of corresponding sides)2
ar(△DEF)/ar(△ABC) = 52/42 = 1/2
Question 27.
ΔABC ~ ΔDEF and ∠A = ∠D = 90°, find the measure of ∠B + ∠F.
Solution:
ΔABC ~ ΔDEF
⇒ ∠A = ∠D = 90°
∠B = ∠E; ∠C = ∠F
Now in ΔABC, ∠A + ∠B + ∠C = 180°
Now putting ∠A = ∠D = 90°
⇒ 90° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 90°
Now putting ∠C = ∠F
⇒ ∠B + ∠F = 90°
Question 28.
Given AB ‖ CD, identify the pair of similar triangles in this image and justify.
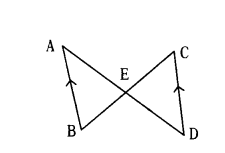
Solution:
∠AEB = ∠CED (Vertically opp. angle)
∴ ∠BEA and ∠CDE are similar by AAA - Similarity rule
ΔBEA ~ ΔCDE
Question 29.
ABC is a triangle in which
p) If AB2 + BC2 = AC2 then
q) BC2 + AC2 = AB2 then
r) CA2 + AB2 = BC2 then
i) ∠A = 90°
ii) ∠B = 90°
iii) ∠C = 90°
A) p - i, q - ii, r - iii
B) p - ii, q - i, r - iii
C) p - iii, q - i, r - ii
D) p - ii, q - iii, r - i
Answer:
D) p - ii, q - iii, r - i
Question 30.
Statement-I: The lengths 3 cm, 4 cm, 5 cm form a right angled triangle. Statement-II: If ‘a’ is the side of an equilateral triangle, then its height is √3 a. Now, choose the correct answer.
(A) Statement-I and Statement-II both are True.
(B) Statement-I and Statement-II both are False.
(C) Statement-I is True. Statement-II is False.
(D) Statement-I is False. Statement-II is True.
Answer:
C) Statement-I is True. Statement-II is False.
Question 31.
Give two different examples of pair of similar figures.
Answer:
(i) Two equilateral triangles.
(ii) Two circles.
Question 32.
"In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides." The above theorem is related to which Mathematician ?
A) Baudhayan
B) Aryabhatta
C) Euclid
D) Bhaskaracfyarya
Answer:
A) Baudhayan
Question 33.
Assertion (A) : The sides of two similar triangles are in the ratio 2 : 5, then the areas of these triangles are in the ratio 4 : 25
Reason (R) : The ratio of the areas of two similar triangles is equal to the square of the ratio of their sides.
A) Both assertion and reason are true and reason is the correct explanation of assertion.
B) Both assertion and reason are true but reason is not the correct explanation of assertion.
C) Assertion is true but reason is false.
D) Assertion is false but reason is true.
Answer:
A) Both assertion and reason are true and reason is the correct explanation of assertion.
10th Class Maths Triangles 2 Marks Important Questions
Question 1.
In the figure, if RS // ID then find AR.
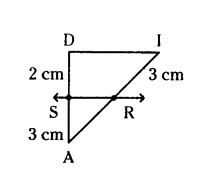
Given,
In ΔADI, RS // ID
By Thales theorem,
AS/DS = AR/IR
3/2 = AR/3
AR = 3×3/2 = 9/2 = 4.5 cm
Therefore AR = 4.5 cm.
Question 2.
In ΔABC, D and E are point on the sides of AB and AC respectively. Such that DE // BC. If AD/DB = 2/3 and AC = 18 cm, find AE.
Solution:
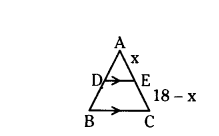
Given in ΔABC, DE // BC, AD/DB = 2/3,
AC = 18 cm
Let AE = x then EC = 18 - x.
In ΔABC, DE // BC
By Thales theorem
AD/DB = AE/EC
2/3 = x/18-x
3x = 2(18 - x)
3x = 36 - 2x
3x + 2x = 36
5x = 36
x = 36/5 = 7.2 cm
Therefore, AE = 7.2 cm.
Question 3.
In the figure, if AB ⊥ BC and DE ⊥ AC. Prove that ΔABC ~ ΔAED.
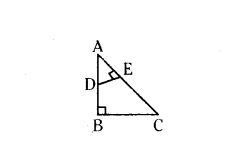
Solution:
Given in ΔABC, ∠B = 90°, ∠E = 90°
that is AB ⊥ BC and DE ⊥ AC.
In ΔABC, ΔAED
∠ABC = ∠AED = 90° (Angle)
∠BAC = ∠DAE (Common angle)
Therefore by Angle-Angle criterian of similarity
ΔABC ~ ΔAED
Question 4.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a tower casts a shadow 30 m long. Determine the height of the tower.
Solution:
Given length of stick AB =10 cm
length of its shadow BC = 8 cm
Height of tower PQ = x cm.
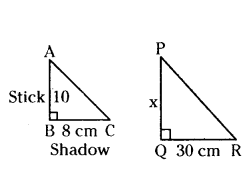
length of the shadow of tower at the same time QR = 30 cm.
By Angle-Angle similarity
ΔABC ~ ΔPQR
then the corresponding sides are in proportion.
AB/PQ = BC/QR
10/x = 8/30
8x = 30 × 10
x = 30×10/8 = 75/2 = 37.5 cm
Therefore, height of tower = 37.5 cm.
Question 5.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts the shadow 28 m long. Find the height of the tower.
Solution:
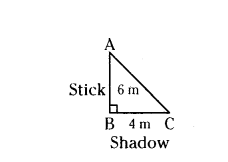
Let length of stick AD = 6 m
Length of its shadow DI = 4 m
Let height of tower SR = x m
and its shadow at the same time BE = 28 m.
By Angle-Angle similarity
ΔADI ~ ΔSRE
then the corresponding sides are in proportion
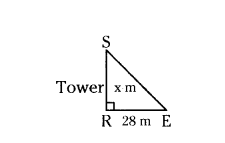
AD/SR = DI/RE
6/4 = x/28
x = 6/4 × 28 = 42 m
Therefore, height of tower = 42 m.
Question 6.
The perimeter of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm find AB.
Solution:
Given ΔABC ~ ΔPQR
So, ratio of the corresponding sides = ratio of their perimeters.
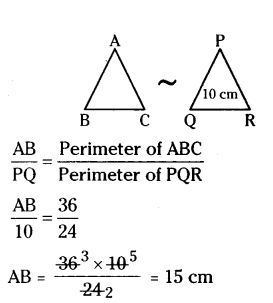
Therefore, AB = 15 cm
Question 7.
Is a square similar to a rectangle? Justify your answer.
Solution:
In a square and rectangle, the corresponding angles are equal. But the corresponding sides are not proportional.
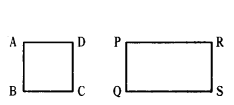
∴ A square and a rectangle are not similar.
Question 8.
In ΔABC, LM//BC and AL/LB = 2/3, AM = 5 cm, find AC.
Solution:
In ΔABC, LM//BC
⇒ AL/LB = AM/MC (By B.P.T)
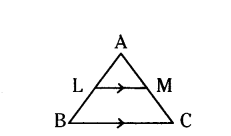
But = AL/LB = 2/3, so AM/MC = 2/3
Given AM = 5 cm and AM : MC = 2 : 3
AM/MC = 2/3 ⇒ 5/MC = 2/3
⇒ MC = 5×3/2 = 15/2 = 7.5
∴ AC = AM + MC = 5 + 7.5 = 12.5 cm
Question 9.
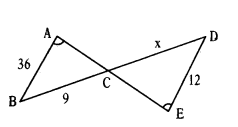
In the figure, ∠BAC = ∠CED, then verify whether the value of ‘x’ is 3 or not.
Solution:
Given : In ΔABC and ΔECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ ∠B = ∠D [∵ Angle sum property]
∴ ΔABC - ΔEDC
⇒ AB/ED = BC/DC = AC/EC
⇒ 36/12 = 9/x
⇒ 36x = 108
⇒ x = 108/36 = 3
Question 10.
In ΔABC, DE ‖ BC and AC = 5.6 cm, AE = 2.1 cm, then find AD : DB.
Solution:
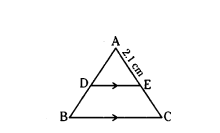
In ΔABC DE ‖ BC,
AE = 2.1 cm
EC = AC - AE = 5.6 - 2.1 = 3.5 cm
As per B.P.T, AD : DB = AE : EC = 2.1 : 3.5 = 3 : 5
Question 11.
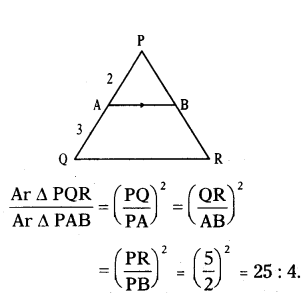
In the given figure, AB ‖ QR and PA = 2 cm, AQ = 3 cm, then find the ratio of areas of ΔPQR and ΔPAB.
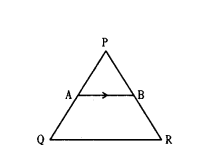
Solution:
Given AB ‖ QR; PA = 2, AQ = 3
then, ΔPQR ~ ΔPAB
∴ PQ = 2 + 3 = 5
∴ Ratio of area of similar triangles is equal to square of ratio of their corresponding sides.
Question 12.
In ΔPQR and ΔXYZ, it is given that ΔPQR ~ ΔXYZ, ∠Y + ∠Z = 90° and XY : XZ = 3 : 4. Then find the ratio of sides in ΔPQR.
Solution:
Given that ΔPQR - ΔXYZ means ∠P = ∠X, ∠Q = ∠Y and ∠R = ∠Z (∵ Corresponding angles are equal)
Similarly PQ/XY = QR/YZ = RP/ZX (∵ Ratio of corresponding sides)
Given that ∠Y + ∠Z = 90°
In AXYZ, ∠X + ∠Y + ∠Z = 180°
∠X + 90° = 180°
∠X = 180° - 90° = 90°
∠X + ∠P = 90° and XY/XZ
∴ ΔXYZ is a right angle triangle.
In a right angle triangle order of sides ratio may be 3 : 4 : 5.
* Remaining length YZ may be 5 units.
Ratio of XY : XZ : YZ = 3 : 4 : 5.
Similarly ratio of sides in ΔPQR is 3 : 4 : 5.
Question 13.
Find the value of ‘x’ in the given figure where ΔABC ~ ΔADE.
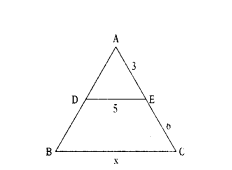
Solution:
ΔABC ~ ΔADE
⇒ AB/AD = BC/XE = AC/AE;
BC = x, DE = 5, AE = 3, AC = 9
By substituting BC/DE = AC/AE
∴ x/5 = 9/3 ⇒ x = 9×5/3 = 15
∴ x = 15 cm
Question 14.
It is given that ΔABC ~ ΔDEF. Is it true
to say that BC/DE = AB/EF ? Justify your answer.
Solution:
Given that ΔABC ~ ΔDEF
∴ AB/DE = BC/EF = AC/DF
(∵ Ratio of corresponding sides of similar triangles are equal)
But BE/DE = AB/EF (given)
∴ Given statement is wrong.
Question 15.
Srivani walks 12 m due East and turns left and walks another 5 m, how far is she from the place she started ?
Solution:
The distance of Srivani from the place she started
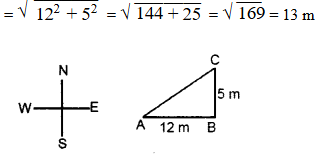
Question 16.
Write the similarity criterion by which the given pair of triangles are similar.
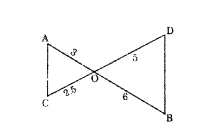
Solution:
OA/OB = 3/6 = 1/2
OC/OD = 2.5/5 = 0.5 = 1/2
OA/OB = OC/OD ⇒∠AOC = ∠BOD
Using SAS - Criterion ∴ ΔOAC ~ ΔOBD)
Question 17.
Madhavi said "All squares are simUar". Do you agree yith her statement ? Justify your answer.
Answer:
Because two polygons with the same number of sides are similar if
i) All the corresponding angles are equal and
ii) All the lengths of the corresponding sides are in the same ratio (or in proportion)
Squares size may not be equal but their ratios of corresponding parts will always be equal.
Question 18.
In the given figure, ABC is a triangle. AD = 3 cm, DB = 5 cm, AE = 6 cm and EC - 10 cm. Is DE ‖ BC ? Justify.
Solution:
AD = 3 cm, DB = 5 cm
AE = 6 cm, as EC = 10 cm
AD/DB = 3/5
AE/EC = 6/10 = 3/5
AD/DB = AE/EC ⇒ DE ‖ BC
Question 19.
The sides of a triangle measure 2√2, 4 and 2√6 units. Is it a right-angled triangle ? Justify.
Solution:
(2√2)2 = 8
(4)2 = 16
(2√6)2 = 24
(2√2)2 + (4)2 - (2√6)2
∴ If sum of squares of two sides of a triangle is equal to the square of the third side, then the triangle is a right angled triangle. (Converse of Pythagorus theorem)
∴ Given triangle is a right-angled triangle.
Question 20.
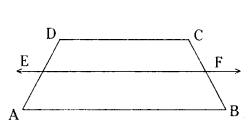
In the given figure, if ABCD is a trapezium in which AB ‖ CD ‖ EF, then
AE BF prove that AE/ED = BF/FC.
Solution:
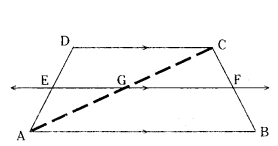
Given : In a trapezium ABCD, AB ‖ DC ‖ EF.
Given: AE/ED = BF/FC
Construction: Join AC which intersects EF at G.
Proof: ΔCAB, GF ‖ AB
FG/BF = CG/AG (by BPT)
BF/FC = AG/CG ..... (1)
In ΔADC, EG ‖ DC
AE/ED = AG/GC (by BPT) .. (2)
BY (1) & (2) AE/ED = BF/FC.
Question 21.
In figure, if AD = 6 cm, DB = 9 cm, AE - 8 cm and EC = 12 cm and ∠ADE=48°, Find ∠ABC.
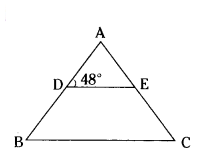
Solution:
In the figure AD = 6 cm
DB = 9cm
AE = 8 cm
EC = 12 cm
∠ADC = 48°
In ΔADE and ΔABC
AD/AB = 6/6+9 = 6/15 = 2/15
AE/AC = 8/8+12 = 8/20 = 2/5
∠A = ∠A (Common angle)
∴ by SAS criterion
ΔADE ~ ΔABC.
∠ADE = ∠ABC (by CPCT)
∴ ∠ABC = 48°
Question 22.
In the figure, altitudes AD and CE of ΔABC intersect each other at the point.
Show that
(i) ΔABD ~ ΔCBE
(ii) ΔPDC ~ ΔBEC
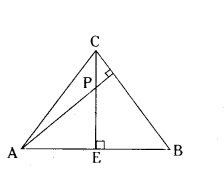
Solution:
i) Given ΔABD and ΔCBE
∠ADB = ∠CEB = 90°
∠B = ∠B (Common angle)
∴ By AA Similarity criterion
ΔADB ~ ΔCBE
ii) In ΔPDC and ΔBEC
∠PDC = ∠BEC = 90°
∠C = ∠C (Common angle)
∴ By AA similarity criterion
ΔPDC ~ ΔBEC.
10th Class Maths Triangles 4 Marks Important Questions
Question 1.
In ΔABC, P and Q are points on sides AB and AC respectively, such that PQ // BC. If AP = 2.4 cm, AQ = 2 cm, AC = 3 cm and BC = 6 cm. Find AB and PQ.
Solution:
Given in ΔABC, PQ // BC and AP = 2.4 cm, AQ = 2 cm, AC = 3 cm and BC = 6 cm
Let BP = x and PQ = y cm
By Thales theorem
AP/BP = AQ/CQ
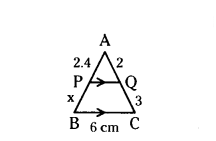
2.4/x = 2/3 and AP/AB = PQ/BC
2.4/x = 2/3 ⇒ 2x = 2.4 × 3 ⇒ x = 2.4×3/2
BP = x = 3.6 cm
∴ AB = AP + BP = 2.4 + 3.6 = 6 cm
Now, AP/AB = PQ/BC
2.4/6 = PQ/6
Therefore, PQ = 2.4 cm
Question 2.
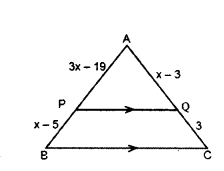
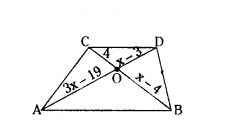
In the given trapezium ABCD, AB // DC. Find the value of x.
Solution:
In the given figure,
ABCD is a trapezium AB // DC.
OA = 3x - 19, OB = x - 3, OC = x - 5 and DO = 3 cm
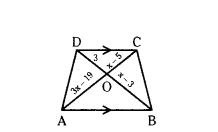
We know that diagonals of a trapezium divide each other proportionally,
AO/CO = BO/DO
3x-19/x-5 = x-3/3
3(3x - 19) = (x - 3) (x - 5)
9x - 19 × 3 = x2 - 5x - 3x + 15
9x - x2 + 8x - 57 - 15 = 0
- x2 + 17x - 72 = 0
x2 - 17x + 72 = 0
x2 - 9x - 8x + 72 = 0
x(x - 9) - 8(x - 9) = 0
(x - 8) (x - 9) = 0
x - 8 = 0 (or) x - 9 = 0
Therefore, x = 8 (dr) x = 9
Question 3.
In the figure gIven AO/OC = BO/OD = 1/2 and AB = 5cm. Find the value of DC.
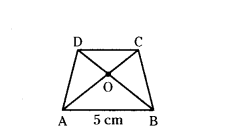
Solution:
In quadrilateral ABCD, diagonals AC and BD are meeting at O.
AO/OC = BO/OD = 1/2 and AB = 5cm.
In ΔAOB and ΔCOD
AO/OC = BO/OD and ∠AOB = ∠COD
by Side-Angle-Side similarity criterion
ΔAOB ~ ΔCOD
OA/OB = OB/OC = AB/DC
1/2 = 5/DC
DC = 2 × 5 = 10 cm
Therefore DC = 10 cm
Question 4.
In the given figure, OA/OC = OD/OB prove that ∠A = ∠C and ∠B = ∠D.
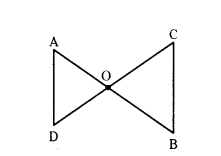
Solution:
Given in ΔAOD and ΔCOB
OA/OC = OD/OB
and ∠AOD = ∠BOC (Vertically opposite angles)
by Side-Angle-Side similarity criterion ΔAOD ~ ΔCOB
If two triangles are similar then their corresponding angles are equal,
i.e., ∠A = ∠C and ∠D = ∠B
Therefore, ∠A = ∠C and ∠B = ∠D.
Question 5.
A girl of height 90 cm is walking away from the base of a lamppost at a speed of 1.2 m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.
Solution:
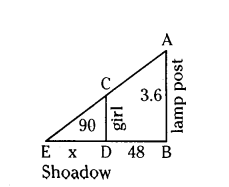
Let AB be the, height of lamp post
AB = 3.6 cm
and height of girl CD = 90 cm = 0.9 m length of the shadow of girl after 4 seconds = x m
length of BD = 1.2 × 4 = 4.8 cm
In ΔABE, ΔCDE
∠B = ∠D = 90° (Angle)
∠E = ∠E (Common angle)
By Angle-Angle similarity criterion
ΔABE ~ ΔCDE
then corresponding sides are in proportion.
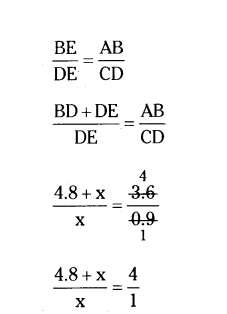
4x = 4.8 + x
4x - x = 4.8
3x = 4.8
x = 4.8/3 = 1.6 cm
Therefore length of shadow of the girls = 1.6 cm.
Question 6.
In the given figure, CD is the perpendicular bisector of AB. EF is perpendicular to CD. AE intersects CD
at G.Prove that CF/CD = FG/DG.

Solution:
In ΔEFC and ΔBDC
∠EFC = ∠BDC = 90°
∠ECF = ∠BCD (Common angle)
by AA Similarity
ΔEFC ~ ΔBDC
by CPST EF/BD = FC/DC.
In ΔEFG and ΔDGA
∠EGF = ∠DGA (VOA)
∠EFG = ∠GDA (= 90°)
by AA Similarity
Δ EFG ~ Δ ADG
we have AD = BD
EF/BD = FG/DG.
FG/DG = CF/CD.
Question 7.
In the given figure, ABCD is a parallelogram. BE bisects CD at M and intersects AC at L. Prove that EL = 2BL.
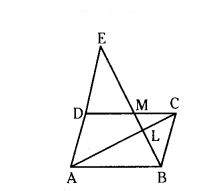
Solution:
Given ΔBMC and ΔEMD
∠BMC = ∠EMD (VOA)
Given MC = DM
∠BCM = ∠EDM (ALA)
∴ ΔBMC ≅ ΔEMD (by ASA)
by CPCT BC = DE
AE = AD + DE = BC + BC = 2BC
∴ ΔBLC ≅ ΔELA (by AA similarity)
EL/BL = AE/BC
by CP/ST = EL/BL = 2BC/BC EL/BL = 2/1
EL = 2BL
Question 8.
In fig 6, if ΔABC ~ ADEF and their sides of lengths (in cm) are marked along them, then find the lengths of sides of each triangles.
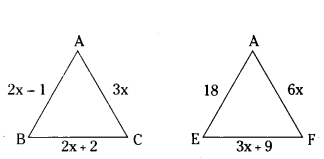
Solution:
ΔABC ~ ΔDEF.

4x - 2 = 18
4x = 20
x = 5
AB = 2 × 5 - 1 = 9.
BC = 2 × 5 + 2 = 12
CA = 3 × 5 = 15
DE = 18
EF = 3 × 5 + 9 = 24.
FD = 6 × 5 = 30
AB = 9 cm, BC = 12 cm, EF = 24 cm
CA = 15 cm, DE = 18 cm, FD = 30 cm.
Question 9.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/OD.
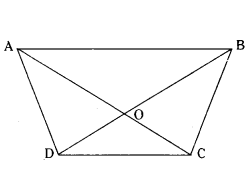
Show that quadrilateral ΔABCD is a trapezium.
Solution:
Given: The diagonals of a quadrilateral ΔBCD intersect each other at the point ‘O’ such that
AO/BO = CO/OD
To prove : ABCD is a trapezium.
Construction: Draw OE ‖ DC such that E lies on BC.
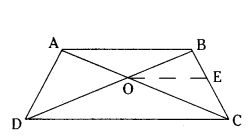
Proof : In ΔBDC
By BPT, BO/OD = BE/EC ... (1)
but AO/CO = BO/DO .... (2)
from (1) & (2)
AO/CO = BE/EC
by the converse of BPT.
OE ‖ AB
Since AB ‖ CE ‖ DC
∴ AB ‖ DC
∴ ΔBCD is a trapezium.
Question 10.
E is a point on the side AD produced of a parallelogram ABCD and BE interesects CD at F. Show that ΔABE ~ ΔCFB.
Solution:
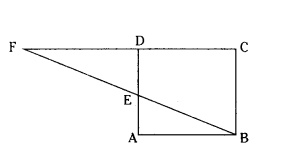
In ΔABE and ΔCFB
∠ABE = ∠CFB (AIA)
∠BAE = ∠BCF (opposite angles of ‖gm)
∴ by AA Similarity criterion
ΔABE ~ ΔCFB.
Question 11.
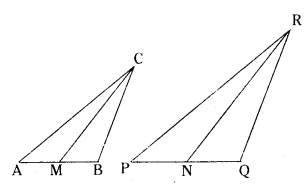
In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ~ ΔPQR, then prove that ΔAMC ~ ΔPNR.
Solution:
Given : ΔABC ~ ΔPQR
CM and RN are medians of ΔABC and ΔPQR respectively.
To prove : ΔAMC ~ ΔPNR
Proof : Given ΔABC ~ ΔPQR, ∠A = ∠P,
∠B = Q, ∠C = ∠R
AB/PQ = BC/QR = CA/RP
AB/PQ = x+y/y+y = 2x/2y = x/y
Let AM = MB = x
In ΔAMC and ΔPNR
x/y = AM/PN
x/y = AB/PQ = CA/RP
AM/PN = CA/RP
∠A = ∠P
by SAS similarity criterion.
ΔABC ~ ΔPNR.
Question 12.
In figure ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.
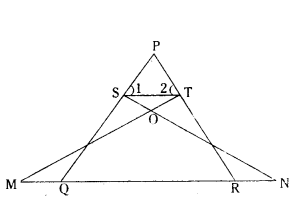
Solution:
Given ∠1 = ∠2
ΔNSQ ≅ ΔMTR
∴ PS = PT
by CPCT, SQ = TR
In ΔPTS & ΔPRQ
∠P = ∠P (Common angle)
∠Q = ∠R (PQ = PR)
by AA similarity
ΔPTS ~ ΔPRQ.
Question 13.
Observe the below figure.
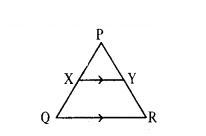
In a ΔPQR, if XY // QR and PX - x - 2, XQ = x + 5, PY = x - 3 and YR = x + 3, then find the value of ‘x’.
Solution:
Given : In ΔPQR, XY // QR and
PX = x - 2, XQ = x + 5, PY = x - 3 and YR = x + 3.
By Basic Proportionality theorem,
If XY // QR then we should have
PX/XQ = PY/YR
∴ x-2/x+5 = x-3/x+3
⇒ (x - 2) (x + 3) = (x - 3) (x + 5)
⇒ x2 + 3x - 2x - 6 = x2 + 5x - 3x - 15
⇒ x2 + x - 6 = x2 + 2x- 15
⇒ x - 6 = 2x- 15
⇒ 2x - x = 15 - 6
⇒ x = 9
∴ The value of x = 9 will make
XY // QR.
Question 14.
In a ΔABC, AD ⊥ BC and AD2 = BD × CD, prove that ΔABC is a right - angled triangle.
Solution:
Given : In ΔABC, AD ⊥ BC and AD2 = BD × CD
RTP : In ΔABC is a right - angled triangle
Proof : AD2 = BD × CD
⇒ AD/BD = CD/AD
∠ADB = ∠CDA = 90°
∴ Δ ADB - ΔCDA (∵ S.A.S Similarity)
In Δ ABD, ∠BAD + ∠ABD = 90° (∵ ∠ADB = 90°)
In Δ ACD, ∠DAC + ∠ACD = 90° (∵ ∠ADC = 90°)
∠ BAD = ∠ACD (∵ pair of corresponding angles)
∠ABD = ∠DAC (∵ pair of corresponding angles)
∴ ∠BAD + ∠DAC = 90°
∠BAC = 90°
Δ ABC is a right - angled triangle.
Question 15.
In ΔABC, PQ ‖ BC and AP = 3x - 19, PB = x - 5, AQ = x + 3, QC = 3 cm. Find x.
Solution:
In Δ ABC PQ ‖ BC
⇒ AP/PB = AQ/QC (∵ Basic proportionality theorem)
3x-19/x-5 = x-3/3
9x - 57 = x2 - 8x + 15
⇒ x2 - 17x + 72 = 0
(x - 8) (x - 9) = 0
x = 8 or x = 9
Question 16.
If the ratio of areas of two equilateral triangles is 25 : 36, then find the ratio of heights of the triangles.
Solution:
For similar triangles
Ratio of area = Ratio of sides
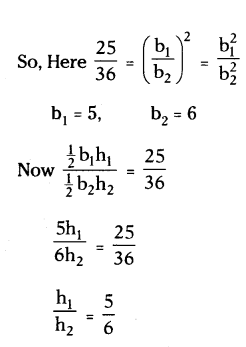
h1 : h2 = 5 : 6
∴ The ratio of heights of the triangles = 5 : 6
Question 17.
In ΔABC, D and E are points on AB and AC respectively. If AB = 14 cm; AD = 3.5 cm, AE = 2.5 cm and
AC = 10 cm, show that DE ‖ BC.
Solution:
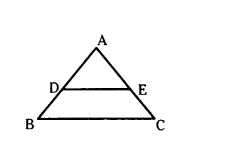
Given AB = 14 cm, AD = 3.5 cm,
AE = 2.5 cm, AC = 10 cm.
BD = AB - AD = 14 - 3.5 = 10.5 cm
EC = AC - AE = 10 - 2.5 = 7.5 cm
AD/DB = 3.5/10.5 = 1/3 .... (1)
AD/DB = 2.5/7.5 = 1/3 ..... (2)
From (1) and (2), AD/DB = AE/EC
∴ DE‖BC (∵ using converse of BPT)
Question 18.
In a rectangle ABCD, AB = 2x - y, BC = 15, CD = 2 and DA = x + 3y, then find the values of x and y.
Solution:
Given that
In a rectangle ΔBCD
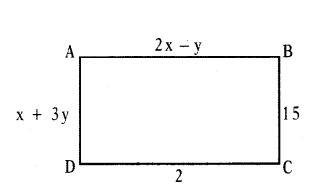
AB = 2x - y
BC = 15; CD = 2; OA = x + 3y
So,
In a rectangle opposite sides are equal
(1) → 2x - y = 2
(2) → x + 3y = 15
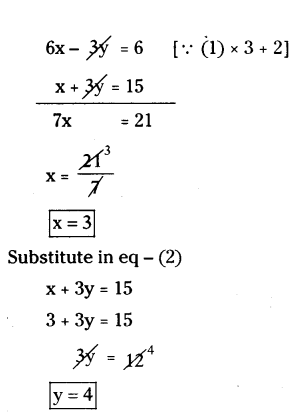
so the value of x is 3 and the value of y is 4.
Question 19.
Observe the below diagram and find the values of x and y.
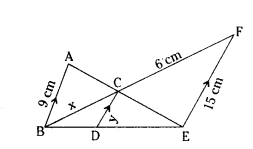
Solution:
ΔABC ~ ΔEFC
x/6 = 9/15 ⇒ x = 9×6/15 = 18/5 = 3.6 cm
ΔBDC ~ ΔBEF
x/9.6 = y/15 ⇒ y = 3.6×15/9.6 = 45/8 = 5.625 cm.
Question 20.
Give two different examples of pair of i) Similar figures, ii) Non - similar
figures.
Solution:
By keeping in view of the definition of similar figures.
(i) Similar figures : 
For any two correct examples for similar figures.
(ii) Non similar figures : 
For any two correct examples for similar figures.
Question 21.
The hypotenuse of a right triangle is 6m more than twice the shortest side. If the third side is 2m less than hypotenuse, find the sides of the triangle.
Solution:
Let the shortest side = ‘x’ m
then its hypotenuse = (2x + 6) m
Third side = 2x + 6 - 2 = (2x + 4) m
then from Pythagoras theorem, we have
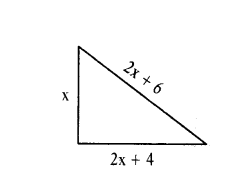
x2 + (2x + 4)2 = (2x + 6)2
⇒ x2 + 4x2 + 16x + 16 = 4x2 + 24x + 36
⇒ x2 + 16x - 24x + 16 - 36 = 0
⇒ x2 - 8x - 20 = 0
⇒ x2 - 10x + 2x - 20 = 0
⇒ x(x - 10)+ 2(x - 10)= 0
⇒ (x - 10)(x + 2) = 0
⇒ x = 10 or x = -2
but x being the length cannot be negative.
So x ? -2, we consider x = 10 only
then the
shortest side = x = 10 m
third side 2x + 4 = 24m
hypotenuse = 2x + 6 = 26 m
Question 22.
A ladder 25 m long reaches a window of building 24 m above the ground. Determine the distance of the foot of the ladder from the building.
Solution:
In a ΔABC, ∠C = 90°
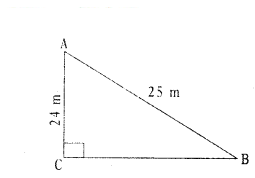
AB = length of ladder = 25m
AC = height of window = 24 m
AB2 = AC2 + BC2
BC2 = AB2 - AC2
= 252 - 242 = (25 + 24) (25 - 24)
= 49 × 1 = 72
∴ BC = 7 m
∴ Distance of the foot of the ladder from the building = 7 m.
Question 23.
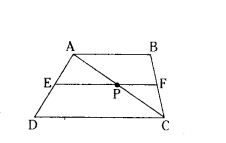
In figure EF ‖ AB ‖ DC, prove that AE/ED = BF/FC.
Solution:
Given in ABCD quadrilateral.
EF ‖ AB ‖ DC
In ΔADC, EP ‖ DC.
By Basic Proportionality theorem,
AE/ED = AP/PC → (1)
In ΔCAB, FP ‖ BA.
By Basic Proportionality theorem,
BF/FC = AP/PC → (2)
From (1) and (2) AE/ED = BF/FC.
Question 24.
In figure, DE ‖ BC and CD ‖ EF. Prove that AD2 = AB × AF.
Solution:
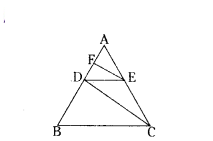
Given in ΔABC,
DE ‖ BC and CD ‖ EF.
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,
AB/AD = AC/AE → (1)
In ΔADC, FE ‖ DC
By Basic Proportionality theorem,
AD/AF = AC/AE → (2)
From (1) and (2) AB/AD = AD/AF AD.AD = AB.AF
Therefore, AD2 = AB.AF.
Question 25.
In a ΔABC, D and E are points on the sides AB and AC respectively such that DE ‖ BC. If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm. Find the length of AC.
Solution:
Given in ΔABC,
AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm and DE ‖ BC.
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,
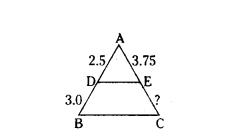
∴ CE = 4.5 cm
AC = AE + CE = 3.75 + 4.5
Therefore, AC = 8.25 cm
Question 26.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE ‖ BC and BD = CE. Prove that ΔABC is isosceles.
Solution:
In ΔABC, DE ‖ BC and BD = CE.
In ΔABC, DE ‖ BC,
By Basic Proportionality theorem,
AD/DB = AE/EC
AD/AE = DB/EC = 1
So, AD/AE = 1
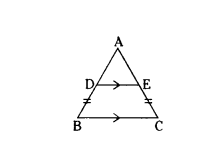
Therefore, AD = AE
So, AD + BD = AE + CE
AB = AC.
In ΔABC, AB = AC
Two sides are equal in ΔABC.
Therefore, ΔABC is an isosceles.
Question 27.
In the given figure AB ‖ CD. If OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4, find x.
Solution:
In quadrilateral ABCD, AB ‖ DC.
So, ABCD is a trapezium.
In trapezium diagonals divide each other proportionately.
OA/OC = OB/OD
3x-19/x-3 = x-4/4
⇒ 4(3x - 19) = (x - 3) (x - 4)
⇒ 12x - 76 = x2 - 4x - 3x + 12
⇒ x2 - 7x + 12x + 88 = 0
⇒ x2 - 19x + 88 = 0
⇒ x2 - 11x - 8x + 88 = 0
⇒ x (x - 11) - 8 (x - 11) = 0
⇒ (x - 8) (x - 11) = 0
Therefore, x = 8 (or) 11.
Question 28.
In figure, QA and PB are perpendiculars to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ.
Solution:
In ΔAOQ, ΔBOP
∠A = ∠B = 90°
∠AOQ = ∠BOP (Vertically opposite angles)
Angle-Angle criterion of similarity
ΔAOQ ~ ΔBOP.
So, corresponding sides are in proportion.
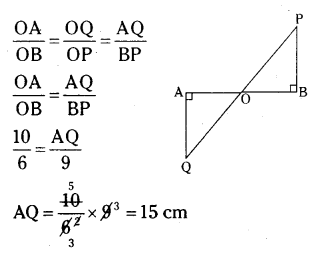
There, AQ = 15 cm.
Question 29.
In figure, considering triangles BEP and CPD. Prove that BP × PD = EP × PC.
Solution:
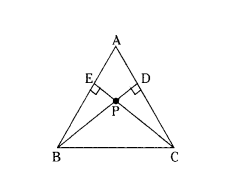
In ΔABC, BD ⊥ AC
and CE ⊥ AB.
In ΔEBP, ΔDCP
∠E = ∠D = 90°
∠EPB = ∠DPC (Vertically opposite angles)
By Angle-Angle criterion similarity
ΔEBP ~ ΔDCP.
So, corresponding sides are in proportion.
BP/PC = EP/PD
Therefore, BP × PD = EP × PC.
Question 30.
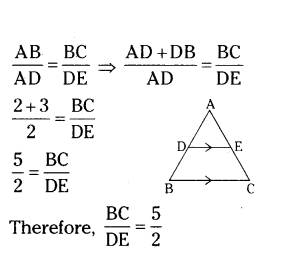
In ΔABC, DE ‖ BC, with D on AB and E on AC. If AD/DB = 2/3, find BC/DE.
Solution:
Given in ΔABC.DE ‖ BC and AD/DB = 2/3
In ΔABC, DE ‖ BC.
By Basic Proportionality theorem,
10th Class Maths Triangles 8 Marks Important Questions
Question 1.
In the given figure BE/AC = BC/BD and ∠1 = ∠2. Prove that ΔABD ~ ΔEBC.
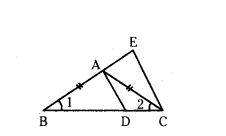
Solution:
Given in ΔBCE,
∠1 = ∠2 and BE/AC = BC/BD
BE/BC = AC/BD → (1)
In ΔMBC, ∠1 = ∠2 and then sides opposite to equal angles are equal.
That is AC = AB → (2)
From (1) and BE/BC = AB/BD
In ΔABD and ΔEBC
∠ABD = ∠EBC = ∠B
and BE/BC = AB/BD
So, by side-angle-side similarity criterion.
Therefore, ΔABD ~ ΔEBC
Question 2.
Given in the trapezium ABCD, AB // DC. If ΔAED ~ ΔBEC then prove that AD = BC.
Solution:
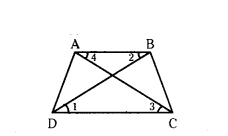
In trapezium ΔBCD, AB // DC and ΔAED ~ ΔBEC. A
In ΔEDC, ΔEBA
∠EDC = ∠EBA
∠1 = ∠2 (Alternate angles)
∠ECD = ∠EAB
∠3 = ∠4 (Alternate angles)
∠CED = ∠AEB (Vertically opposite angles)
By A - A similarity criterion
ΔEDC ~ ΔEBA
Corresponding sides are in proportion
ED/EC = BE/AE → (1)
But,.given ΔAED ~ ΔBEC
then the corresponding sides are in proportion ED/EC = AE/BE = AD/BC → (2)
From (1) and (2)
ED/EC = BE/AE = AE/BE
BE2 = AE2
BE = AE ⇒ AE/BE = 1
Put BE = AE in (2)
ED/EC = 1 = AD/BC
AD/BC = 1
Therefore AD = BC.
Question 3.
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side, of the perpendicular are similar to each other and to the original triangle. Also prove that the square of the perpendicular is equal to the product of the length of the two parts of the hypotenuse. That is
i) ΔAOB ~ ΔBOC
ii) ΔADB ~ ΔABC
iii) ΔBOC ~ ΔABC
iv) BD2 = AD.DC
v) AB2 = AD.AC
vi) BC2 = CD.AC
Solution:
Given in ΔABC, ∠B = 90° and BD ⊥ AC
i) ∠ABD + ∠DBC = 90° → (1)
In ΔBOC,
∠BDC + ∠DBC + ∠C = 180°
90° + ∠DBC + ∠C = 180°
∠DBC + ∠C = 180° - 90° = 90° → (2)
From (1) and (2) ∠ABD = ∠C.
In ΔADB, ∠BDC,
∠ABD = ∠C and ∠ADB = ∠BDC = 90°
by Angle-Angle similarity criterion
ΔADB ~ ΔBDC → (3)
ii) In ΔADB and ΔABC
∠ADB = ∠ABC = 90° (Angle)
and ∠A = ∠A (Common angle)
by Angle-Angle similarity criterion.
ΔADB - ΔABC → (4)
iii) In ΔBDC and ΔABC
∠BDC = ∠ABC = 90° (Angle)
∠C = ∠C (Common angle)
By Angle-Angle similarity criterion
ΔBDC ~ ΔABC → (5)
From (3), (4) and (5)
ΔADB ~ ΔBDC ~ ΔBDC - ΔABC
iv) We proved ΔADB ~ ΔBDC then corresponding sides are in proportion
AD/BD = BD/DC
BD.BD = AD.DC
BD2 = AD.DC
v) We proved ΔADB ~ ΔABC
AD/AB = AB/AC
AB2 = AD.AC
vi) We proved ΔBDC ~ ΔABC
BC/AC = DC/BC
BC2 = AC.DC
Question 4.
In ΔABC given AD and BE are perpendiculars to BC and AC respectively show that
i) ΔADC ~ ΔBEC
ii) CA.CE = CB.CD
iii) ΔABC ~ ΔDEC
iv) CD.AB = CA.DE
Solution:
In ΔABC, AD ⊥ BC and BE ⊥ AC
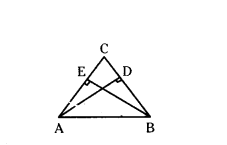
i) In ΔADC and ΔBEC
∠ADC = ∠BEC = 90° (Angle)
∠C = ∠C (Common angle)
By Angle-Angle similarity criterion
ΔADC - ΔBEC
ii) The corresponding sides are in proportion
CA/CB = CD/CE → (1)
iii) In ΔABC, ΔDEC
From(1) AC/BC = DC/EC (or) AC/DC = BC/EC
By Side - Angle - Side similarity criterion ΔABC ~ ΔDEC.
iv) Corresponding sides are in proportion
AB/DE = AC/DC
Therefore, AB.DC = AC.DE
Question 5.
i) State and prove the "Basic Proportionality theorem".
ii) Using the theorem, find the length of AE, if AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm.
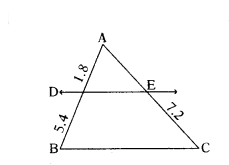
Solution:
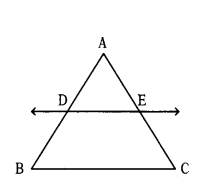
i) If a line is drawn parallel to one side of a triangle to intersecting the other two sides, in distinct points, then the other two sides are divided in the sgme ratio.
Given : A triangle ABC in which DE ‖ BC and DE intersects AB in D and AC in E.
To prove: AD/DB = AE/EC
Construction : Join BE, CD and draw EF ⊥ AB, DG ⊥ AC.
Proof : In ΔEAD and ΔEDB, here as EF is perpendicular to AB, therefore, EF is the height for both of triangles EAD and EDB.
Now,
Area of ΔEAD = 1/2 (base × height)
= 1/2 × AD × EF
Area of ΔEDB = 1/2 (base × height)
= 1/2 × DB × EF
Area(ΔEAD)/Area (ΔEDB) = = AD/DB .... (1)
Similarly, Area(ΔEAD)/Area (ΔECD) .... (2)
∵ ΔDBE, ΔECD are on the same base DE and between the same parallels DE ‖ BC, we have
Area of ΔDBE = Area of ΔECD
Hence, (1) = (2)
i.e., AD/DB = AE/EC (Q.E.D).
ii) Using the theorem to find the length of
AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
From the theorem, AD/BD = AE/EC
⇒ AE = (AD)(EC)/BD = 1.8×7.2/5.4 = 2.4
∴ AE = 2.4cm
Question 6.
ABC is a right angled triangle which is right angled at C. Let AB = c, BC = a, CA = b and let p be the length of perpendicular from C on AB. Prove that c = ab/p.
Solution:
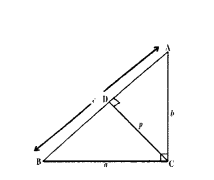
CD ⊥ AB and CD = p.
Also area of ΔABC = 1/2 × AB × CD
= 1/2 cp
Also area of ΔABC = 1/2 × BC × AC
= 1/2 ap
1/2 cp = 1/2 ap ⇒ cp = ap ⇒ c = ab/p
Question 7.
In given figure if PQ ‖ BC and PR ‖ CD. prove that
i)AR/AD = AQ/AB
ii)QB/AQ = DR/AR.
Solution:
In ΔABC, PQ ‖ BC.
By Basic Proportionality theorem,
AQ/AB = AP/AC → (1)
In ΔACD, PR ‖ CD
By Basic Proportionality theorem,
AP/AC = AR/AD → (2)

Question 8.
In a ΔABC, D and E are points on the sides AB and AC respectively such that DE ‖ BC. If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3. Find the value of x.
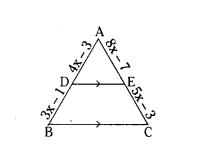
Solution:
In ΔABC, DE ‖ BC
AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,
AD/BD = AE/CE
⇒ 4x-3/3x-1 = 8x-7/5x-3
⇒ (4x - 3) (5x - 3) = (8x - 7) (3x - 1)
⇒ 20x2 - 12x - 15x + 9 = 24x2 - 8x - 21x + 7
⇒ - 24x2 + 20x2 - 27x + 29x + 9 - 7 = 0
⇒ - 4x2 + 2x + 2 = 0
⇒ - 2 (2x2 - x - 1) = 0
⇒ 2x2 - x - 1 = 0
⇒ 2x2 - 2x + x - 1 = 0
⇒ 2x(x- 1) + 1 (x- 1) = 0
⇒ (2x + 1) (x - 1) = 0
⇒ 2x + 1 = 0 and x - 1 = 0
x = - 1/2 (or) 1
Length cannot be negative.
Therefore, x = 1
Question 9.
ABCD is a trapezium, in which AB ‖ DC and its diagonals intersect each other at point ‘O’. Show that OA/OB = OC/OD.
Solution:
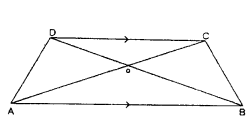
In Δ OAB, Δ OCD
∠AOB = ∠COD (∵ pair of vertically Opp. Angles)
∠OAB = ∠OCD (∵ Pair of alternate angles)
∠OB A = ∠ODC (∵ Pair of alternate angles)
∴ Δ OAB ~ Δ OCD (∵ AAA similarity)
∴ OA/OC = OB/OD ⇒ OA/OB = OC/OD
Question 10.
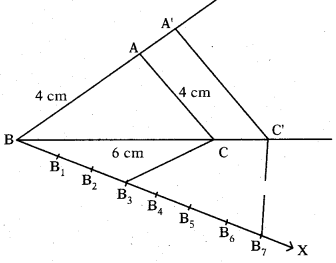
Construct an equilateral triangle XYZ of side 5 cm and construct another triangle similar to ΔXYZ, such that each of its sides is 4/5 of the sides of ΔXYZ.
Solution:
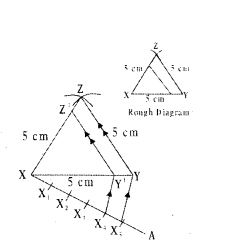
Steps of construction :
- Draw an equilateral triangle XYZ with side 5 cm.
- Draw a ray XA such that ∠YXA is an acute angle.
- Draw X1, X2, X3, X4, X5 arcs on XA such that XX1 = X1X2 = ... = X4X5
- Join X5 and Y.
- Draw a parallel line to X5Y through X4 to meet XY at Y’.
- Draw a parallel line to YZ through Y’ to meet XZ at Z’.
- Δ XY’ Z’ is required similar triangle.
AP 10th Class Maths Important Questions Chapter 6 Similar Triangles
Question 1.
Is a square similar to a rectangle ? Justify your answer.
Solution:
In a square and rectangle, the corresponding angles are equal. But the corresponding sides are not proportional.
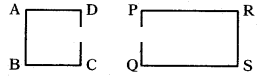
∴ A square and a rectangle are not similar
Question 2.
In ΔABC LM‖BC and AL/LB = 2/3, AM = 5 cm, find AC.
Solution:
In ΔABC, LM // BC
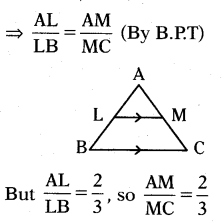
Given AM = 5 cm and AM : MC = 2:3
AM/MC = 2/3 ⇒ 5/MC = 2/3
⇒ MC = 5×3/2 = 15/2 = 7.5
∴ AC = AM + MC = 5 + 7.5 = 12.5 cm
Question 3.
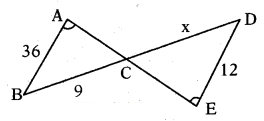
In the figure, ∠BAC = ∠CED, then verify whether the value of ‘x’ is 3 or not.
Solution:
Given: In ΔABC and ΔECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ LB ¿D [∵ Angle sum property]
∴ ΔABC ~ ΔEDC
⇒ AB/ED = BC/DC = AC/EC ⇒ 36/12 = 9/x
⇒ 36x= 108 ⇒ x= 108/36 = 3
Question 4.
In ΔABC, DE ‖ BC and AC = 5.6 cm, AE = 2.1 cm, then find AD : DB.
Solution:
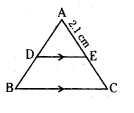
In ΔABC DE ‖ BC,
AE = 2.1 cm
EC = AC - AE
= 5.6 - 2.1 = 3.5 cm
As per B.P.T, AD : DB = AE : EC
= 2.1 : 3.5 = 3:5
Question 5.
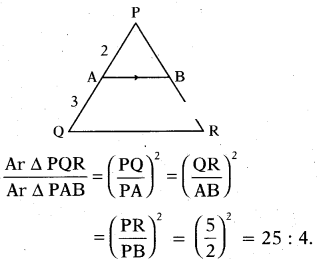
In the given figure, AB‖QR and PA = 2 cm, AQ = 3 cm, then find the ratio of areas of ΔPQR and ΔPAB.
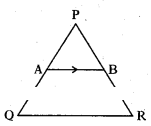
Solution:
Given AB ‖ QR; PA = 2, AQ = 3
then, APQR ~ APAB
∴ PQ = 2 + 3 = 5
∴ Ratio of area of similar triangles is equal to square of ratio of their corre-sponding sides.
Question 6.
Give two different examples of pair of i) Similar figures, ii) Non - similar figures. Mar. ’17
By keeping in view of the definition of similar figures.
Solution:
By keeping in view of the definition of similar figures.
(i) Similar figures :
For any two correct examples for similar figures.
(ii) Non similar figures :
For any two correct examples for non similar figures.
Question 7.
Define A.A. and S.S.S. rules for similarity of two triangles in your own words.
Solution:
A.A. similarity : If two angles of a triangle are equal to two corresponding angles of another triangle, then the two triangles are similar.
S.S.S. similarity : If in two triangles, sides of one triangle are proportional to the sides of other triangle, then their corresponding angles are equal and hence the two triangles are similar.
Question 8.
The hypotenuse of a right triangle is 6m more than twice the shortest side. If the third side is 2m less than hypotenuse, find the sides of the triangle.
Solution:
Let the shortest side = ‘x’m
then its hypotenuse = (2x + 6) m
Third side = 2x + 6 - 2 = (2x + 4) m then from Pythagoras theorem, we have
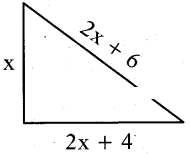
x2 + (2x + 4)2 = (2x + 6)2
⇒ x2 + 4x2 + 16x + 16 = 4x2 + 24x + 36
⇒ x2 + 16x - 24x + 16 - 36 = 0
⇒ x2 - 8x - 20 = 0
⇒ x2 - 1 Ox + 2x - 20 = 0
⇒ x(x- 10) + 2 (x- 10) = 0
⇒ (x - 10) (x + 2) = 0
⇒ x = 10 or x = -2
but ‘x’ being the length cannot be negative.
So x ? -2, we consider x = 10 only then the
shortest side = x = 10m
third side = 2x + 4 = 24 m
hypotenuse = 2x + 6 = 26m
Question 9.
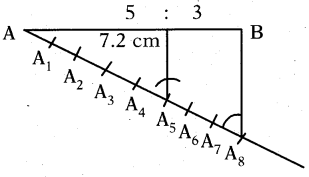
Draw a line segment of length 7.2 cm. and divide it in the ratio 5 : 3 using compasses and ruler.
Solution:
Question 10.
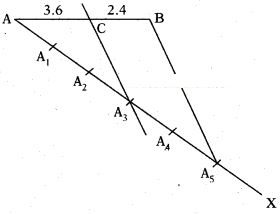
Construct a triangle of sides 4.2 cm, 5.1 cm and 6 cm. Then construct a tri¬angle similar to it, whose sides are 2/3 of corresponding sides of the first tri¬angle.
Solution:
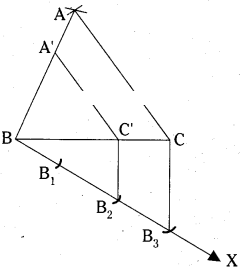
- Draw a triangle ABC, with sides AB = 4.2cm,BC = 5.1 cm,CA = 6cm.
- Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
- Locate 3 points B,, B2, B3 on BX so that BB1 = B1B2 = B2B3.
- Join B3,C an draw a line through B2 parallel to B3C intersecting BC at C1.
- Draw a line through .C1 parallel to CA intersect AB at A1.
- A1BC1 is required triangle.
Question 11.
Construct a triangle PQR, where QR = 5.5cm,∠Q= 65°andPQ = 6cm. Then draw another triangle, whose sides are 2/3 times of the corresponding sides of ΔPQR.
Solution:
Construction Steps:
- Draw a triangle ΔPQR with sides QR = 5.5cm, ∠Q = 65°and PQ = 6cm.
- Draw a ray OX making an acute angle with QR on the side opposite to vertex P
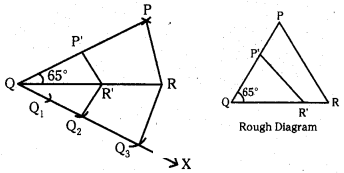
- Locate 3 points Q1 Q2 Q3 on QX. So that QQ1 = Q1Q2 = Q2Q3
- Join Q3,R and draw a line through Q2 parallel to Q3R intersecting QR at R.
- Draw a line through ‘R’ parallel to PR intersect PQ at P.
- ΔP’QR’ is required triangle.
Question 12.
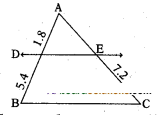
i) State and prove the "Basic Propor-tionality theorem".
ii) Using the theorem, find the length of AE, if AD = 1.8 cm, BD .= 5.4 cm, EC = 7.2 cm.
Solution:
If a lines is drawn parallel to one side of a triangle to intersecting the other two sides, in distinct points, then the other two sides are divided in the same ratio.
Given : A triangle ABC in which DE ‖ BC and DE intersects AB in D and AC in E.
To prove : AD/DB=AE/EC
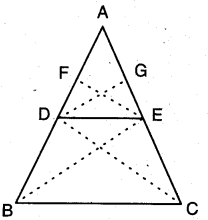
Construction : Join BE, CD and draw EF ⊥ AB, DG ⊥ AC.
Proof : In ∆EAD and ∆EDB, here as EF is perpendicular to AB, therefore, EF is the height for both of triangles EAD and EDB.
Now,
Area of ∆EAD = 1/2 (base x height)
= 1/2 x AD x EF
Area of ∆EDB = 1/2 (base x height)
= 1/2 x DB x EF

∵ ∆DBE, ∆ECD are on the same base DE and between the same parallels DE ‖ BC, we have
Area of ∆DBE = Area of ∆ECD
Hence, (1) = (2)
i.e., AD/DB=AE/EC
ii) Using the theorem, to find the length of AE
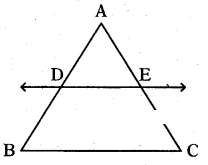
AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
From the theorem, AD/BD = AE/EC
⇒ AE = (AD)(EC)/BD = 1.8×7.2/5.4 = 2.4 cm
∴ AE = 2.4 cm
Question 13.
Draw ΔABC with sides 4.3 cm, 5.2 cm and 6.5 cm and then construct a tri-angle similar to ΔABC, whose sides are 3/5 th of the corresponding sides.
Solution:
Constructing a similar triangle whose sides are 3/5 of corresponding sides.
Steps of construction:
1) Draw a triangle ΔABC with sides AB = 4.3 cm, BC = 5.2 cm and AC = 6.5 cm
2) Draw a ray BX making an acute angle with BC on the side opposite to vertex ‘A’.
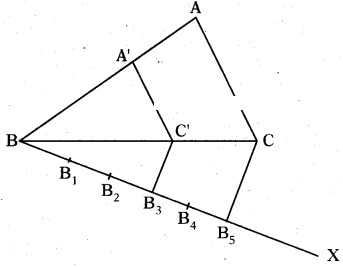
3) Locate 5 points B1; B2, B3, B4, B5 on the ray BX Such that
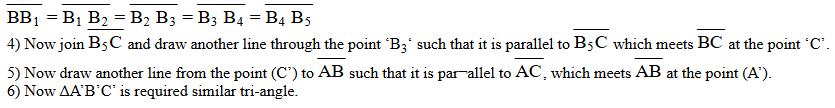
Question 14.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 4 cm. Draw a triangle similar to ΔABC with its sides 3/4 times of the corresponding sides of ΔABC.
Solution:
Question 15.
Divide the line segment AB = 6 cm in the ratio of 3 : 2. Explain the con-struction procedure.
Solution:
Steps to construct:
1) Draw a line segment AB = 6 cm
2) Draw a line AX such that ∠BAX is an acute.
3) Make 5 equal parts on AX. (3 + 2)
4) Now join B with last part A5.
5) Then draw a line from A3 to AB which meets at ‘C’ such that it is parallel to BA5.
6) So ‘C’ is the point which divides AB in the ratio of 3 : 2
Question 16.
In the given ΔABC, E and F are two points on AB and AC respectively. Then verify whether EF ‖ BC or not in the following cases.
Solution:
From the converse of Thales theorem
EF ‖ BC if AE/EB=AF/FC
Case I) AE = 3.9, EB = 3,
AF = 3.6, CF = 2.4
Then AE/EB=3.9/3=1.3/1;AF/FC = 3.6/2.4 = 3/2
So AE/EB≠AF/FB then EF ∦ BC
Case II) AE = 4, EB = 4.5;
AF = 8 and CF = 9
So AE/EB=4/4.5=8/9 and AF/FB=8/9
So then AE/EB=AF/FB
hence EF ‖ BC.
Question 17.
In the given figure BC ‖ DE and AD = DB = 3.4 and AC = 14.
So find AE and EC.
Solution:
In the given ΔABC, DE ‖ BC is given.
So from Thales theorem,
AD/DB=AE/EC
In this problem, AD = DB = 3.4 is given.
And also AC = 14 is given.
So AD/DB=AE/EC
⇒ 3.4/3.4=AE/EC
⇒ AE = EC
But AC = 14 is given.
AC = AE + EC = 2AE = 14
⇒ AE = EC = 7 cm
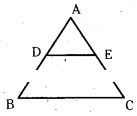
Question 18.
In given ΔABC points D and E are mid points of AB and AC and also BC = 6 cm then find DE.
Solution:
As shown in the figure D, E are mid points of AB and AC.
Then AD = BD, AE = EC
∴ AD/BD=AE/EC hence DE ‖ BC (From the Converse of Thales theorem)
AD/AB=DE/BC=AE/EC
⇒ AD/2AD=DE/6
⇒ 2DE = 6 and DE = 3 cm
∴ DE = 3 cm
Question 19.
In the given figure, AB ‖ CD ‖ EF given AB = 73cm,DC=ycm,EF 4.5cm, BC = x cm. Calculate the values of x and y.
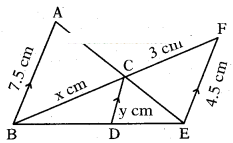
Solution:
Given that, AB ‖ CD ‖ EF and
AB = 7.5 cm, DC = y cm
According to Thales theorem
Δ??CDE ~ Δ??ABE

From (1) and (2)
7.5-y/7.5=y/4.5
7.5 y = (7.5) (4.5)-4.5 y
12y = (7.5) (4.5) = 33.75
y = 33.75/12 = 2.8125
From (2)
y/4.5 = x/x+3; 2.8/4.5 = x/x+3
4.5 x = (2.8) x + 8.4
4.5 x - (2.8) x = 8.4
1.7 x = 8.4
x = 8.4/1.7 = 5 (approx)