7th Lesson Coordinate Geometry Class 10 Important Questions with Solutions
10th Class Maths Coordinate Geometry 1 Mark Important Questions
Question 1.
Write the distance between two points (x1, y1) and (x2y, 2).
Solution:
Distance between two points = √(x2, x1)2 + (y2y, 1)2.
Question 2.
Write the distance from the origin to (x, y).
Solution:
Distance from origin to (x, y) = √x2+y2
Question 3.
Find the distance between the points (-6, 7) and (-1, -5).
Solution:
Let A(-6, 7) and B(-1, -5) are points. Distance between the two points
= √(x2, x1)2 + (y2y, 1)2
x1 = - 6, x2 = -1, y1 = 7 and y2 = - 5
AB = √(-1-(-6))2+(-5-7)
= √(-1+6)2+(-12)2
= √52+144 =√169 = 13 units
Distance AB = 13 units
Question 4.
Find the distance (4, 3) from the origin.√x2+y2
Solution:
Let A(4, 3) be any point.
Distance from origin to (x, y) =
x = 4, y = 3
OA = √42+32 =√16+9= √25 = 5 units
Therefore, distance from the origin to A(4, 3) is 5 units.
Question 5.
Write the section formula.
Solution:
P(x, y) = (m1x2+m2x1/m1+m2 , m1y2+m2y1/m1+m2)
Question 6.
Write the midpoint of (x1, y1) and (x2, y2).
Solution:
Mid point = (x1+x2/2 , y1+y2/2)
Question 7.
If A(x1, y1), B(x2, y2) and C(x3, y3) are vertices of AABC, then write its cen-troid.
Solution:
Centroid of the ∆ABC = (x1+x2+x3/3 , y1+y2+y3/3)
Question 8.
If end points of a diameter of a circle are (-5, 4) and (1, 0) then find the radius of the circle.
Solution:
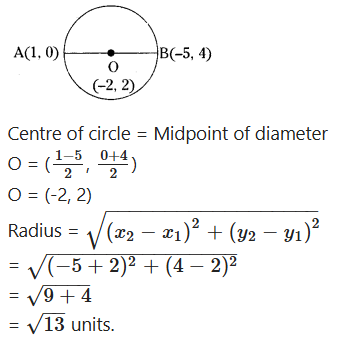
Question 9.
Two statements are given, one labelled as Assertion (A) and the other is labelled as Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below:
Assertion (A) : If the points A(4, 3) and B(x, 5) lie on a circle with centre 0(2, 3), then the value of x is 2.
Reason (R) : Centre of a circle is the mid-point of each chord of the circle.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion
(A).
B) Both Assertion (A) and Reason (R) . are true, but Reason (R) is the correct explanation of the Assertion (A).
C) Assertion (A) is true, but Reason (R) is false.
D) Assertion (A) is false, but Reason (R) is true.
Solution:
C) Assertion (A) is true, but Reason (R) is false.
A : A(4, 3), B(x, 5), Centre O(2, 3)
AO = BO
AO2 = BO2
(2 - 4)2 + (3 - 3)2 = (2 - x)2 + (3 - 5)2
4 = (2 - x)2 + 4
R is false 2 - x = 0
x = 2
Question 10.
Find the distance of the point (-6, 8) from origin.
Solution:
(0, 0), (-6, 8)
(x1 y1), (x2 y2)
Distance = √(-6)2+82 = √36+64
= √100 = 10
Question 11.
Find the distance of the point (-1, 7) from X-axis.
Solution:
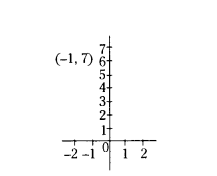
Distance = 1 unit
Question 12.
If (3, √3), B(0, 0)and C(3, k) are the three vertices of an equilateral triangle ABC, then find the value of k.
Solution:
A(3, √3), B(0, 0), C(3, k)
∆ABC is an equilateral triangle
AB = BC = AC
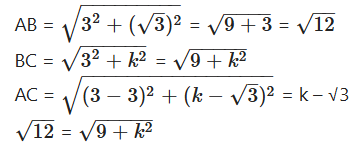
12 = 9 + k2 ⇒ k2 = 12 - 9 ⇒ k2 = 3
k = ±√3
Question 13.
Three vertices of a parallelogram ABCD are A(1, 4), B(-2, 3) and C(5,8). Find the ordinate of the fourth vertex D.
Solution:
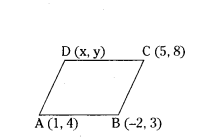
Midpoint of AC = Midpoint of BD
(1+5/2, 4+8/2) = (-2+x/2, y+3/2)
(3, 6) = (-2+x/2, y+3/2)
-2+x/2 = 3, y+3/2 = 6
6 = -2 + x, 12 = y + 3
x = 8 ⇒ y = 9
Ordinate = 9
Question 14.
Points A(-1, y) and B(5, 7) lie on a circle with centre O(2, -3y). What are the values of y ?
Solution:
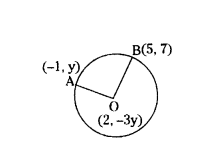
OA2 = OB2
(2 + 1)2 + (- 3y - y)2 = (2 - 5)2 + (- 3y - 7)2
9 + 16y2 = 9 + (3y + 7)2
16y2 = 9y2 + 42y + 49
9y2 + 42y + 49 - 16y2 = 0
-7y2 + 42y + 49 = 0
-7(y2 - 6y - 7) = 0
y2 - 6y - 7 = 0
y2 - 7y + y - 7 =
y(y - 7) + 1(y - 7) = 0
(y + 1) (y - 7) = 0
y = -1, 7
Question 15.
If A(4, -2), B(7, -2) and C(7, 9) are the vertices of a ∆ABC, then ∆ABC is
A) equilateral triangle
B) isosceles triangle
C) right angled triangle
D) isosceles right angled triangle
Solution:
C) right angled triangle
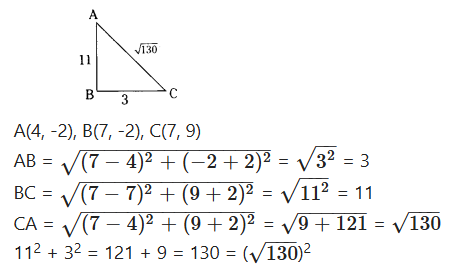
∴ ∆ABC is an right angled triangle.
Question 16.
The line segment joining the points P(-3, 2) and Q(5, 7) is divided by the Y-axis in the ratio
A) 3 : 1
B) 3 : 4
C) 3 : 2
D) 3 : 5
Solution:
D) 3 : 5
P(-3, 2), Q(5, 7)
PQ is divided by Y-axis then (m1x2+m2x1/m1+m2) = 0
m1x2 = -m2x1
m1/m2 = -x1/x2 = 3/5 = 3 : 5
Question 17.
Find the distance between the points (a cos0+b sin6,0) and (0, asin6-bcos6).
Solution:
A (a cos θ + b sin θ, 0)
B (0, a sin θ - b cos θ)
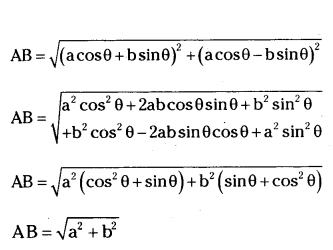
Question 18.
What is the value of p, for the points A(3, 1), B(5,p) and C(7, -5) are collinear?
Solution:
A(3, 1), B(5, p), C(7, -5)
AB slope = BC slope
y2-y1/x2-x1 = y2-y1/x2-x1
p-1/5-3 = -5-p/7-5
p-1/2 = -5-p/2
p - 1 = -5 - p
2p = -4
P = -2
Question 19.
Find the point p on X-axis equidistant from the points A(-1, 0) and B(5, 0).
Solution:
A(-1, 0), B(5, 0)
Let P(x, 0)
AP2 = BP2
(-1, 0) (x, 0) = (5, 0) (x, 0)
(x+ 1)2 = (x - 5)2
x2 + 2x + 1 = x2 - 10x + 25
2x + 10x = 25 - 1
12x = 24
x = 2
∴ Point P = (2, 0)
Question 20.
Find the co-ordinates of the point which is reflection of point (-3, 5) in X-axis.
Answer:
(3, -5)
Question 21.
If the point p(6, 2) divides the line segment joining A(6, 5) and B(4, y) in the ratio 3 : 1, then find the value of y.
Solution:
A(6, 5), B (4, y), P(6, 2)
m1 : m2 = 3 : 1
(m1x2+m2x1/m1+m2, m1y2+m2y1/m1+m2) = (6, 2)
m1y2+m2y1/m1+m2 = 2
3(y) + 1(5) = 2m1 + 2m2
3y + 5 = 2(3) + 2(1)
3y + 5 = 8 ⇒ 3y = 3
⇒ y = 1
Question 22.
Find the distance between the points (3, -2) and (-3, 2).
Solution:
A(3, -2), B(-3, 2)
(x1, y1), (x2, y2)
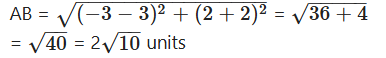
Question 23.
If A(3, √3 ), B(0, 0) and C(3, k) are the three vertices of an equilateral triangle ABC, then find the value of k.
Solution:
A(3, √3), B(0, 0), C(3, k)
AB2 = BC2 = AC2
9 + 3 = 9 + k2 = 0 + (k - √3)2
12 = 9 + k2
12 - 9 = k2
k = ±√3
Question 24.
A point (x, 1) is equidistant from (0,0) and (2, 0). Find the value of x.
Solution:
A(x, 1), B(0, 0), C(2, 0)
AB2 = AC2
(0 - x)2 + (0 - 1)2 = (2 - 0)2 + 0
x2 + 1 = 4
x2 = 3
x = ±√3
Question 25.
What is the ratio in which the point (4, 0) divides the line segment joining the points (4, 6) and (4, -8)?
Solution:
(4, 6), (4, -8) and p(4, 0)
(x1, y1), (x2, y2), (4, 0)
m1 : m2
m1y2+m2y1/m1+m2 = 0
m1y2 = -m2y1
m1/m2 = -y1/y2 = -6/-8 = 3/4
m1 : m2 = 3 : 4
Question 26.
The vertices of a triangle OAB are 0(0, 0), A(4, 0) and B(0,6). The median AD is drawn on OB. Find the length AD.
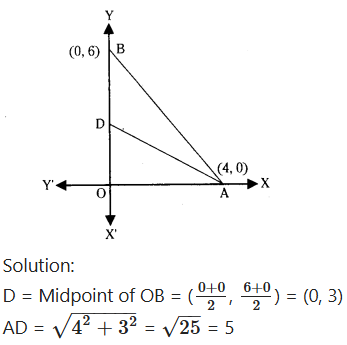
Question 27.
The origin divides the line segment AB joining the points A(1, -3) and B(-3, 9) in the ratio.
A) 3 : 1
B) 1 : 3
C) 2 : 3
D) 1 : 1
Solution:
B) 1 : 3
A(1, -3), B(-3, 9)
(x1, y1), (x2, y2)
m1 : m2
(m1x2+m2x1/m1+m2, m1y2+m2y1/m1+m2) = (0, 0)
m1x2 = -m2x2
m1/m2 = -x1/x2 = -1/-3 = 1/3
m1 : m2 = 1 : 3
Question 28.
The perpendicular bisector of a line segment A(-8, 0) and B(8, 0) passes through a point (0, k). Find the value of ok.
Solution:
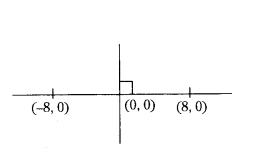
∴ k = 0 only
Question 29.
A circle of radius 3 units is centered at (0, 0). Which of the following points lie outside the circle ?
A) (-1, -1)
B) (0, 3)
C) (1, 2)
D) (3, 1)
Solution:
D) (3, 1)
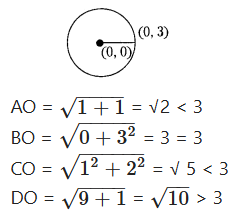
∴ (3, 1) lies outside of circle.
Question 30.
Find the value of a, for which point p(a/3, 2) is the mid-point of the line
segment joining the points Q(-5, 4) and R(-1, 0).
Solution:
Midpoint of QR = P(a/3, 2)
Q(-5, 4), R(-1, 0)
(-5+2/2 + 4+0/2) = (a/3, 2)
-3 = a/3
a = -9
Question 31.
Assertion : The point (0, 4) lies on Y-axis.
Reason (R): The x-coordinate of a point on Y-axis is zero.
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Answer:
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
Question 32.
What is the perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0)?
Solution:
A(0, 4), B(0, 0), C(3, 0)
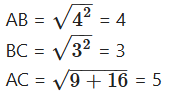
∴ Perimeter = 3 + 4 + 5 = 12
Question 33.
Assertion : The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by X-axis is 1 : 2.
Reason (R): As formula for the internal division is (mx2+nx1/m+n, my2+ny1/m+n)
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
A(2, -3), B(5, 6)
(x1, y1), (x2, y2)
X-axis divides AB
m1y2+m2y1/m1+m2 = 0
m1y2 : -m2y1
m1/m2 = -y1/y2 = 3/6 = 1 : 2
‘A’ is true, ‘R’ is true.
Question 34.
Find the co-ordinate of the point p dividing the line segment joining the poins A(1, 3) and B(4, 6) internally in the ratio 2 : 1.
Solution:
A(1, 3), B(4, 6)
(x1, y1), (x2, y2)
m1 : m2 = 2 : 1
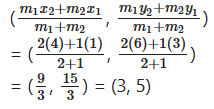
Question 35.
The mid-point of (3p, 4) and (-2, 2q) is (2, 6). Find the value of p + q.
Solution:
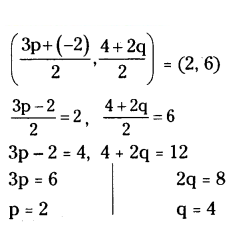
p + q = 2 + 4 = 6
Question 36.
Find the mid point of the line segment joining the points (-5, 7) and (-1, 3).
Solution:
Midpoint = (x1+x2/2, y1+y2/2)
= (-5-1/2, 7+3/2) = (-3, 5)
Question 37.
The coordinate of a point A on Y-axis is 5 and B has coordinates (-3, 1) from length of AB = _______ units.
Solution:
Let A(0, 5), B(-3, 1)
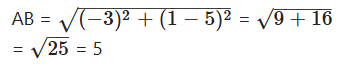
Question 38.
Find the midpoint of the line segment joining the point A(cos2α, 0), B(0, sin2α).
Answer:
(cos2α/2, sin2α/2)
Question 39.
Assertion (A) : The midpoint of the line segment joining the points A(-1, 1), B(1, 3) is (9, 3).
Reason (R): Midpoint of (a, b) and (c, d) = (a+c/2, b+d/2)
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Answer:
D) A is false, R is true.
Question 40.
Assertion (A) : The distance between the points (1, 0) and (-1, 0) is 2 units.
Reason (R) : Any point on Y-axis will be (0, 0).
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Answer:
C) A is true, R is false.
Question 41.
Assertion (A) : If (6, 1), (4, 4) and (-1, 3) are three vertices of a parallelogram respectively then the fourth vertex is (0, 0).
Reason (R) : The diagonals of a para-llelogram are not equal.
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true; but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Answer:
C) A is true, R is false.
Question 42.
Assertion (A) : A point on Y-axis which is equidistant from the points (5, -2) and (-3, 2) is (0, -2).
Reason (R) : All sides of an equilateral triangle are equal.
Choose the correct answer.
A) Assertion (A) is true and Reason (R) is true and R is the correct explanation of A.
B) A is true and R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Answer:
B) A is true and R is true, but R is not the correct explanation of A.
Question 43.
Identify the distance between A(8, 3) and B (4, 3) from the following :
A) 12
B) 0
C) 4
D) 6
Answer:
C) 4
Question 44.
Write the nearest point to origin,
i) (2, -3)
ii) (5, 0)
iii) (0, -5)
iv) (1, 3)
Answer:
(1, 3)
Question 45.
The distance of a point (3, 4) from the origin is how many units ?
Answer:
5 units.
Question 46.
Find the distance between the points (x1, y1) and (x2, y2) which are on the line parallel to Y - axis.
Answer:
|y - y2| or |y2 - y1|
Question 47.
If the distance between the points (3, k) and (4, 1) is √10, then find the value of k.
Answer:
4 (or) - 2.
Question 48.
Write a formula to the coordinates of the point which divides the line joining (x1, y1) and (x2, y2) in the ratio m : n internally.
Answer:
P = (mx2+nx1/m+n, my2+ny1/m+n)
Question 49.
Assertion : (0, 2) is a point on Y-axis.
Reason : Every point on Y-axis is at a distance of zero units from the Y-axis.
Now, choose the correct answer.
(A) Both Assertion and Reason are true. Reason is supporting the Assertion.
(B) Both Assertion and Reason are true, but Reason is not supporting the Assertion.
(C) Assertion is True, but Reason is False.
(D) Assertion is False, but Reason is True.
Answer:
A) Both Assertion and Reason are true.
Reason is supporting the Assertion.
Question 50.
Mid point of a line joining the two points (0, 0) and (4, 6) is ...... .
Solution:
Mid point of line joining (0, 0) and (4, 6)
= (x1+x2/2, y1+y2/2)
= (0+4/2, 0+6/2) = (2, 3)
Question 51.
Identify the distance between A(8, 3) and B (4, 3) from the following :
A) 12
B) 0
C) 4
D) 6
Answer:
C) 4
10th Class Maths Coordinate Geometry 2 Marks Important Questions
Question 1.
If the point A(4, 3) and B(x, 5) are on the circle with centre origin, find value of x.
Solution:
Given A(4, 3) and B(x, 5) are on the circle with centre O(0,0)
then radius OA = OB

x2 + 25 = 25
x2 = 25 - 25 = 0
Therefore, x = 0
Question 2.
Find a point on the y-axis which is equidistant from the point A(6, 5) and B(-4, 3).
Solution:
Let the point on the y-axis is P(0, y)
Given A(6, 5) and B(-4, 3) are equidistant from the point P(0, y)
That is AP = BP
Distance AP = Distance BP
Distance between two points
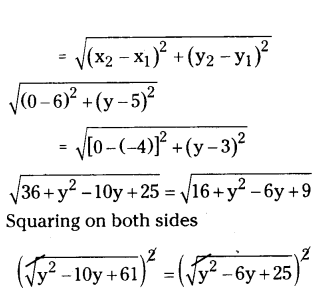
y2 - 10y + 61 = y2 - 6y + 25
- 10y + 6y = 25 - 61
- 4y = -36
y = 36/4 = 9
Therefore midpoint on y-axis P is (0, 9).
Question 3.
Find the midpoint (5, 3) and (-1, 4).
Solution:
Given points A(5, 3) and B(-1, 4)

Question 4.
Find the coordinates of the centroid of a triangle whose vertices are (0,6), (8,12) and (1,0).
Solution:
Given A(0, 6), B(8, 12) and C(1, 0) are the vertices of ∆ABC.
If (x1, y1), (x2, y2) and (x3, y3) are the vertices of a triangle, then its centroid
G = (x1+x2+x3/3, y1+y2+y3/3)
x1 = 0, x2 = 8, x3 = 1, y1 = 6, y2 = 12 and y3 = 0
Centroid (G) = (0+8+1/3, 6+12+0/3)
= (9/3, 18/3)
= (3, 6)
Therefore, centroid of ∆ABC is (3, 6).
Question 5.
Find the coordinates of the point which divides the join of A(-1, 7) and B(4, -3) in the ratio 2 : 3.
Solution:
Given points
A(-1, 7), B(4, -3)
(x1, y1), (x2, y2)
Ratio = 2 : 3
= m1 : m2
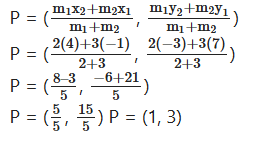
Question 6.
If the points A(2, 3), B(-5, 6), C(6, 7) and D(p, 4) are the vertices of a parallelogram ABCD, find the value of P.
Solution:
The diagonals of a parallelogram will bisect each other.
Midpoint of AC = Midpoint of BD
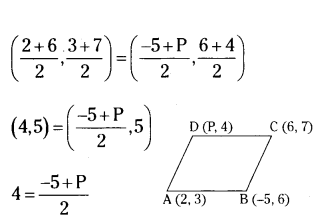
8 = -5 + P ⇒ P 8 + 5 ⇒ P = 13
Question 7.
A line intersects Y-axis and X-axis at point P and Q, respectively. If R(2, 5) is the mid-point of the line segment PQ, then find the coordinates of P and Q.
Solution:
Let P(x, 0), Q(0, y), R(2, 5)
Midpoint of PQ = R(2, 5)
(x+0/2, 0+y/2) = (2, 5)
x/2 = 2, y/2 = 5
x = 4, y = 10
∴ P = (4, 0), Q = (0, 10)
Question 8.
Find the coordinates of the point which divides the line segment joining the points (7, -1) and (-3, 4) internally in the ratio 2 : 3.
Solution:
Let
(7, -1) B(-3, 4)
(x1, y1), (x2, y2)
Ratio = 2 : 3
= m1 : m2
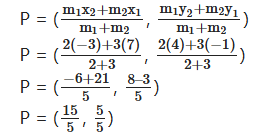
⇒ P = (3, 1)
∴ Required point (3, 1)
Question 9.
Find the value(s) of y for which the distance between the points A(3, -1) and B(11, y) is 10 units.
Solution:
Let A(3, -1), B(11, y)
given AB = 10
AB2 = 102 = 100
(11 - 3)2 + (y + 1)2 = 100
64 + (y + 1)2 = 100
(y + 1)2 = 100 - 64
⇒ (y + 1)2 = 36
y + 1 = √36
⇒ y + 1 = ± 6
y + 1 = 6 (or) y + 1 = -6
y = 5 (or) y = -7
Question 10.
Find the value(s) of ‘x’ so that PQ = QR, where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Solution:
Let P(6, -1), Q(1, 3), R(x, 8)
PQ = QR
PQ2 = QR2
(1 - 6)2 + (3 + 1)2 = (x - 1)2 + (8 - 3)2
25 + 16 = (x - 1)2 + 25
x - 1 = √16
⇒ x - 1 = ± 4
x - 1 = 4 (or) x - 1 = - 4
x = 5 (or) x = -3
Question 11.
The vertices of a triangle are (-2. 0), (2, 3) and (1, -3). Is the triangle equilateral, isosceles or scalene ?
Solution:
Let the vertices of triangle are A(-2, 0), B(2, 3), C(1, -3)
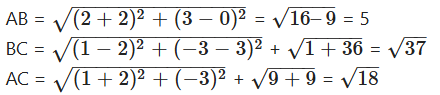
AB ≠ BC ≠ AC
∴ ∆ABC is a scalene triangle.
Question 12.
Find the coordinates of the point p which divides the join of A(-2, 5) and B(3, -5) in the ratio 2 : 3.
Solution:
Given points
A(-2, 5), B(3, -5)
(x1, y1), (x2, y2)
Ratio = m1 : m2 = 2 : 3
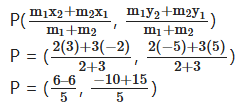
⇒ P = (0, 1)
Question 13.
If (1, p/3) is the mid-point of the line segment joining the points (2, 0) and (0, 2/9) then show that the line 5x + 3y + 2 = 0 passes through the point (-1, 3p).
Solution:
Let A (2, 0), B(0, 2/9)
Let C(1, p/3) in the midpoint of AB
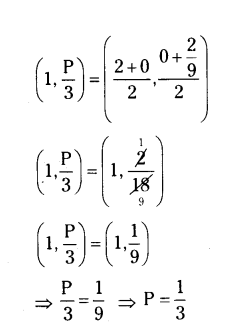
Question 14.
P and Q are the points with co-ordinates (2, -1) and (-3, 4). Find the co-ordinates of the point R such that
PR is 2/5 of PQ.
Solution:
Let
P(2, -1), Q(-3, 4)
(x1, y1), (x2, y2)
PR = 2/5 of PQ.

Question 15.
Show that A(1, 2), B(5, 4), C(3, 8) and D(-1, 6) are vertices of parallelogram ABCD.
Solution:
Given points A(1, 2) B(5, 4) C(3, 8) D(-1, 6)
Distance between two points
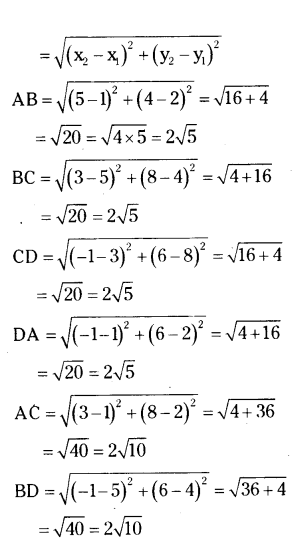
AB = BC = CD = AD and AC = BD
ABCD is a square.
Every square is a parallelogram
∴ ABCD is a parallelogram.
Question 16.
Show that the points A(3, 0), B(6, 4) and C(-1, 3) are vertices of a right-angled triangle.
Solution:
Given A(3, 0), B(6, 4), C(-1, 3)
Distance between two points
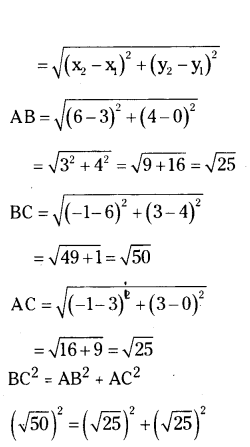
50 = 25 + 25 ⇒ 50 = 50
∴ The given points are vertices of right angled triangle.
Question 17.
Find a relation between x and y such that the point p(x, y) is equidistant from the points A(-5, 3) and B(7, 2).
Solution:
P(x, y), A(-5, 3) and B(7, 2)
Given PA = PB
PA2 = PB2
(x + 5)2 + (y - 3)2 = (x - 7)2 + (y - 2)2
x2 + 10x + 25 + y2 - 6y + 9 = x2 - 14x + 49 + y2 - 4y + 4
10x - 6y + 34 = -14x - 4y + 53
10x + 14x - 6y + 4y = 53 - 34
24x - 2y = 19
∴ The required relation is 24x - 2y - 19 = 0
Question 18.
Find the value of k if the point P(0, 2) is equidistant from (3, k) and (k, 5).
Solution:
Let P(0, 2), A(3, k) B(k, 5)
Given PA = PB
PA2 = PB2
(3 - 0)2 + (k - 2)2 = (k - 0)2 + (5 - 2)2
9 + k2 - 4k + 4 = k2 + 9
- 4k + 4 = 0 ⇒ -4k = -4 ⇒ k = 1
Question 19.
Find the quadrant in which the line segment joining the points (7, -6) and (3, 4) is the ratio 1 : 2 internally.
Solution:
Given points
(7, -6), (3, 4)
(x1, y1), (x2, y2)
m1 : m2 = 1 : 2
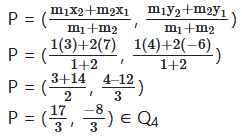
∴ The point lies in Q4.
Question 20.
Find the fourth vertex of a parallelogram PQRS whose three vertices are P(-2, 3), Q(6, 7) and R(8, 3).
Solution:
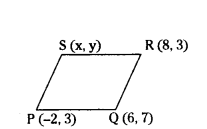
In a parallelogram, diagonals bisect each other.
∴ Midpoint of PR = Midpoint of QS
(-2+8/2, 3+3/2) = (6+x/2, 7+y/2)
(6/2, 6/2) = (6+x/2, 7+y/2)
6 = 6 + x
x = 6 - 6
x = 0
6 = 7 + y
7 + y = 6
y = 6 - 7 = -1
∴ Fourth vertex = (0, -1)
Question 21.
Find the distance between the points (0, 0) and (a, b).
Solution:
Given points are (0, 0) and (a, b). Distance lormula
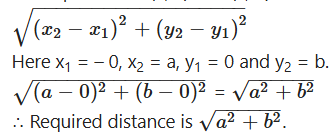
Question 22.
Find the mid point of the line segment formed by the points (- 5, 5) and (5, -5).
Solution:
Formula for the mid point of line segment formed bv [x1+x2/2, y1+y2/2] here x1 = -5, y1 = 5 and x2 = 5, y2 = -5
∴ Mid point = [-5+5/2, 5-5/2] = [0/2, 0/2] = [0, 0]
Question 23.
A (0, 3), B (k, 0) and AB = 5. Find the positive value of k.
Solution:
Distance = √(x2-x1)2+(y2-y1)2
5 = √(k-0)2+(0-3)2
25 = k2 + 9
k2 = 16
⇒ k = ±4
∴ Positive value of k is 4.
Question 24.
Find the distance between the points (1, 5) and (5, 8).
Solution:
(1, 5) (5, 8)
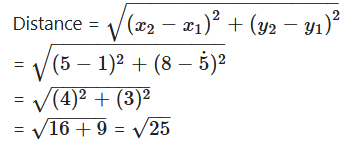
= 5 units.
Question 25.
What is the other end of the diameter of the Circle, whose centre is (1, 2) and one end point of the diameter is (3, 4) ?
Solution:
Let the other end point of diameter be (x, y).
(3+x/2, 4+y/2) = (1, 2)
3+x/2 = 1
3 + x = 2
x = 2 - 3 = - 1
4+y/2 = 2
4 + y = 4
y = 4 - 4 = 0
∴ The required point is (-1, 0).
Question 26.
Find the co-ordinates of the point, which divides the line segment joining (2, 0) and (0, 2) in the ratio 1 : 1.
Solution:
x1 = 2 ; x2 = 0 ; y1 = 0 ; y2 = 2
Point divides the line segment joining (2, 0) and (0, 2) in the ratio 1 : 1
or mid point = (x1+x2/2, y1+y2/2)
= (2+0/2, 0+2/2)
= (1, 1)
Question 27.
Find the distance between (a cos θ, 0) and (0, a sin θ).
Solution:
To find the distance between the points (a cos θ, 0) and (0, a sin θ) we use the formula.
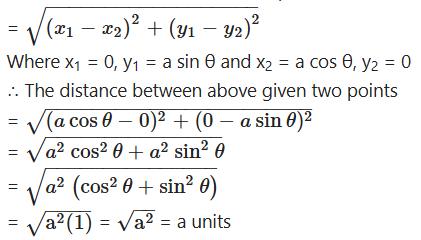
(∵ sin2 θ + cos2 θ = 1)
Question 28.
If A(4, 0), B(0, y) and AB = 5, find the possible values of y.
Solution:
A(4,0), B(0, y) and AB = 5
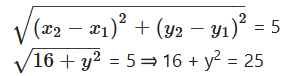
y2 = 25 - 16 = 9
y = ± √9 = ± 3
Possible values of y are 3 or - 3.
Question 29.
Find the radius of the circle with centre (3, 2) and passes through (4, - 1).
Solution:
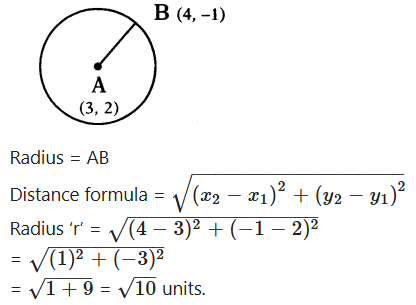
Question 30.
Find the radius of the circle whose cen-tre is (3,2) and passes through (- 5, 6).
Solution:
Given : A circle with centre A (3, 2) passing through B (- 5, 6).

Question 31.
What is the distance between (0, - sin x) and (- cos x, 0) ?
Solution:
Distance between (0, - sin x) and (- cos x, 0)
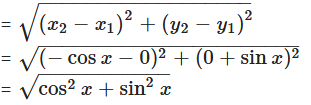
= √1
= 1 unit
Question 32.
Find the mid point of the line segment joining the points (3, 0) and (-1, 4).
Solution:
Mid point of (x1 y1), (x2, y2)
= (x1+x2/2, y1+y2/2)
∴ Mid point of (3, 0) and (-1, 4)
= (3-1/2, 4+0/2) = (2/2, 4/2)
= (1, 2)
Question 33.
Find the midpoint of the line segment joining the A(- 2, 3), B(0, 7).
Solution:
Given
A(- 2, 3) B(0, 7)
x1, y1 x2, y2
Mid-point of AB = (x1+x2/2, y1+y2/2)
= (-2+0/2, 3+7/2)
= (-1, 5)
Question 34.
Find the distance between the two points (7, 8) and (- 2, 3).
Solution:
A(x1 y1) = (7, 8) B(x2, y2) = (-2, 3)
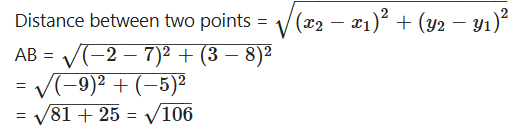
Question 35.
The base BC of an equilateral ∆ABC lies on the y-axis. The coordinates of C are (0, -3). If the origin is the mid-point of the base BC, what are the co-ordinates of A and B ?
Solution:
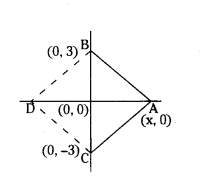
To satisfy mid point B(0, 3) is taken.
BC = 6 units
Let A(x, 0)
AB = √x2+9
BC = √(-3-3)2 = √36
AB2 = BC2
x2 + 9 = 36 ⇒ x2 = 27 ⇒ x = ±3√3
A(±3√3, 0) , B(0, 3)
Question 36.
If the point p(k, 0) divides the line segment joining the points A(2, -2) and B(-7, 4) in the ratio 1 : 2 then find the value of k.
Solution:
P(k, 0) divides line joining
A(2, -2), B(-7, 4)
(x1 y1)> (x2, y2)
m1 : m2 = 1 : 2
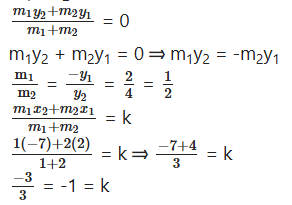
∴ k = -1
10th Class Maths Coordinate Geometry 4 Marks Important Questions
Question 1.
Show that A(6, 4), B(5, -2) and C(7, -2) are the vertices of an isosceles triangle. Also find the length of the median through A.
Solution:
Given A(6, 4), B(5, -2) and C(7, -2) are the vertices of an isosceles triangle ABC.
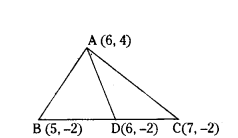
Distance between two points
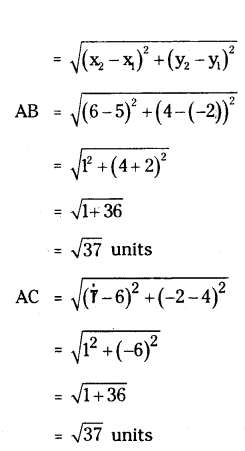
AB = AC = √37 units
Therefore ∆ABC is isosceles.
Let D be the mid-point of BC.

Therefore, length of the median AD = 6 units.
Question 2.
If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p.
Solution:
Given A(0,2) is the equidistant from the points B(3, p) and C(p, 5).
That is AB = AC
AB2 = AC2
Distance between two points
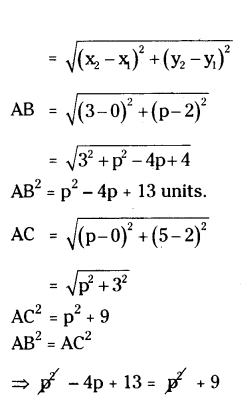
⇒ -4p = 9 - 13
⇒ -4p = -4 ⇒ p = -4/-4 = 1
Therefore p = 1
Question 3.
Determine the ratio in which the line 3x + y - 9 = 0 divides the segment join-ing the points (1, 3) and (2, 7).
Solution:
Let C(x, y) divides the line segment join¬ing the points A(l, 3) and B(2, 7) in the ratio k : 1 and C lies on 3x + y - 9 = 0. Section formula
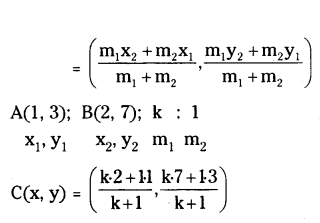
= (2k+1/k+1, 7k+3/k+1)
But given C(x, y) lies on 3x + y - 9 = 0
3 = (2k+1/k+1, 7k+3/k+1) - 9 = 0
⇒ 3(2k+1)+(7k+3)-9(k+1)/k+1 = 0
⇒ 6k + 3 + 7k + 3 - 9k - 9 = 0
⇒ 13k - 9k + 6 - 9 = 0 ⇒ 4k - 3 = 0
∴ k = 3/4
⇒ k : 1 = 3/4 : 1 = 3 : 4
Therefore dividing ratio is 3 : 4.
Question 4.
If A(-2, -1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram. Find the values of a and b.
Solution:
Given A(-2, -1), B(a, 0), C(4, b) and D(1,2) are the vertices of a parallelogram ABCD.
In parallelogram diagonals bisect each other.
That is mid-point of AC = mid-point of BD.
Midpoint = (x1+x2/2, y1+y2/2)
AC mid-point = BD mid-point
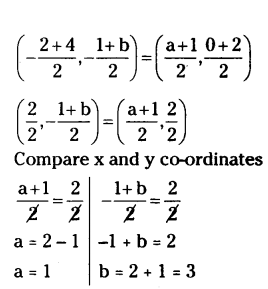
Therefore a = 1 and b = 3
Question 5.
Find the ratio in which die point (2, y) divides the line segment joining the points A(-2, 2), B(3, 7). Also find the value of y.
Solution:
Let P(2, y) can divide the line segment joining by the points A(-2,2), B(3, 7) in the ratio nij: m2.
Section formula
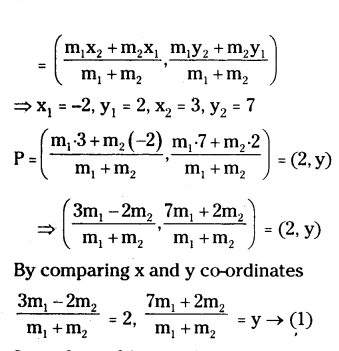
3m1 - 2m2 = 2(m1 + m2)
3m1 - 2m2 = 2m1 + 2m2
1m1 = 4m2
m1/m2 = 4/1 = 4 : 1
Therefore, m1 : m2 = 4 : 1
Put m1 : m2 = 4 : 1 in
7m1+2m2/m1+m2 = y ⇒ 7(4)+2(1)/4+1 = y
⇒ 28+2/5 = y ⇒ y = 30/5 = 6
∴ y = 6.
Question 6.
If A and B are (1, 4) and (5, 2) respectively, find the coordinates of P
when
AP/BP = 3/4.
Solution:
Let P(x, y) can divide the line joining by the points A(1, 4), B(5, 2) in the ratio AP : BP = 3 : 4
Section formula
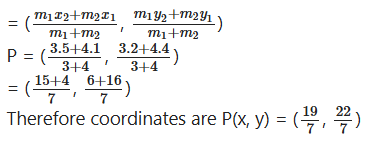
Question 7.
Do the points A(3, 2), B(-2, -3) and C(2, 3) form alriangle ? If so, name the type of triangle formed.
Solution:
Given points are A(3, 2), B(-2, -3) and C(2, 3)
Distance between two points

From the above, AB + BC > AC, AC + BC > AB and AB + AC > BC
Therefore, A, B and C form a triangle.
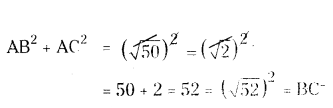
So, AB2 + AC2 = BC2
Therefore, ∆ABC is right angle triangle and ∠A is the right angle.
Question 8.
Show that the points (1, -1), (5, 2) and (9, 5) are collinear.
Solution:
Let A(1,-1), B(5, 2) and C(9, 5) are given points.
Distance between two points

So, 10 = 5 + 5
AC = AB + BC
Therefore. A, B, C are collinear points.
Question 9.
Find a point on the x-axis which is equidistant from the points (7, 6) and (-3, 4).
Solution:
Let a point on the x-axis is P(x, 0) which is equidistant from the points A(7, 6) and B(-3, 4)
that is AP = BP
AP2 = BP2
Distance between two points
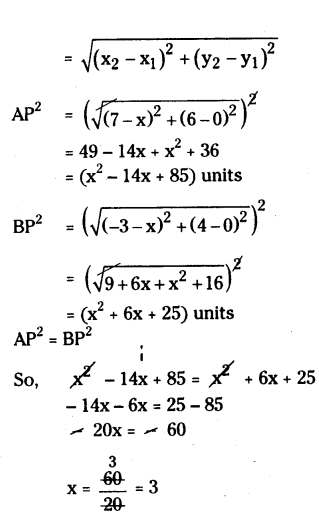
x = 3
Therefore required point is P(3, 0).
Question 10.
Find the centre of the circle passing through (6, -6), (3, -7) and (3, 3).
Solution:
Let A(6, -6), B(3, -7) and C(3, 3) are the points on the circle which are the vertices of ∆ABC.
Let P(x, y) be the centre of the circle.
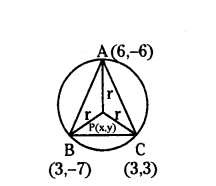
then AP = BP = CP
that is AP2 = BP2 = CP2
Distance between two points
= √(x2-x1)2+(y2-y1)2
AP2 = BP2
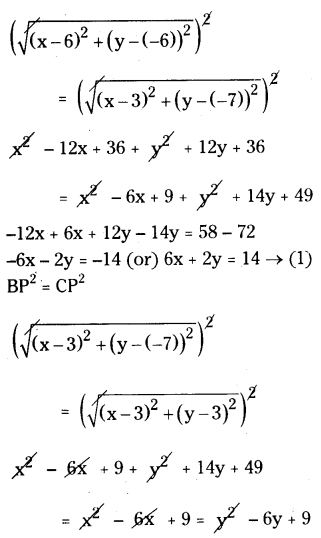
+ 14y + 58 = - 6y + 18
+ 14y + 6y = 18 - 58 = - 40
+ 20y + - 40
y = -40/20
Put y = 2 in (1) ⇒ 6x + 2 (-2) = 14
⇒ 6x = 14 + 4
⇒ 6x = 18
⇒ x = 18/6 = 3
Therefore centre of the circle P(x, y) = (3, -2)
Question 11.
The coordinates of one end of the diamter of a circle is (4, -1) and the co-ordinates of centre of the circle is (1, -3). Find the coordinates of the other end of the diameter.
Solution:
Let the two end of the diameter of a circle are A(4, -1) and B(x, y).
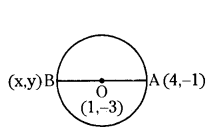
Centre of the circle O(1, -3)
Midpoint of AB = Centre of the circle.
Mid-point = ((x1+x2/2, y1+y2/2))
= (4+x/2, -1+y/2) = (1, -3)
by equating the x and y-coordinates
4+x/2 = 1
4 + x = 2 × 1
x = 2 - 4 = -2
-1+y/2 = -3
- 1 + y = -3 × 2
y = - 6 + 1 = 5
Therefore other end of the diameter B(x, y) = (-2, 5).
Question 12.
Two vertices of a triangle are (3, -5) and (-7, 4). It Its centroid is (2, -1) then find the third vertex.
Solution:
Let the vertices of ∆ABC are A(-3, 5), B(-7, 4) and C(x, y) and its centroid G = (2, -1)
Centroid of the triangle
= (x1+x2+x3/3, y1+y2+y3/3)
Centroid of ∆ABC
= (3+(-7)+x/3, -5+4+y/3) = G = (2, -1)
= (3-7+x/3, -1+y/3) = (2, -1)
By equating the x, y- coordinates
-4+x/3 = 2
-4 + x = 2 × 3
x = 6 + 4 = 10
-1+y/3 = -1
-1 + y = -1 × 3
y = -3 + 1 = -2
Therefore, third vertex of the triangle C(x, y) = (10, -2).
Question 13.
Determine the ratio in which the point P(a, +2) divides the line segment joining the points A(-4, 3) and
B(2, -4). Also find the value of ‘a’.
Solution:
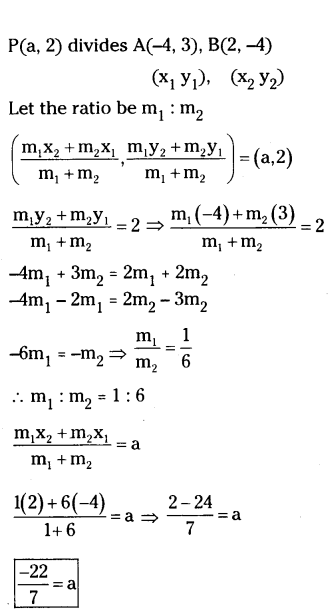
Question 14.
In the given figure, in ∆ABC points D and E are mid-points of sides BC and AC respectively. If given vertices are A(4, -2), B(2, -2) and C(-6, -7), then verify the result DE = 1/2 AB.
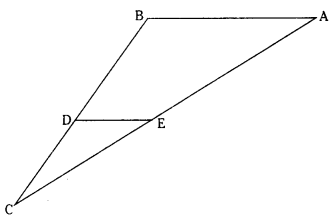
Solution:
Let A(4, -2), B(2, -2), C(-6, -7)
D - Midpoint of BC

Question 15.
If the point C(-1, 2) divides internally the line segment joining A(2, 5) and B(x, y) in the ratio 3 : 4, find the coordinates of B.
Solution:
Let C(-1, 2)

Question 16.
If the mid-point of the line segment joining the points A(3, 4) and B(k, 6) is p(x, y) and x + y - 10 = 0, find the value of k.
Solution:
Given points A(3, 4) and B(k, 6)
Midpoint of AB = P(x, y)
(3+k/2, 4+6/2) = (x, y)
3+k/2 = y ⇒ y = 5
Given x + y - 10 = 0
3+k/2 + 5 - 10 = 0 ⇒ 3+k/2 - 5 = 0
3+k/2 = 5 ⇒ 3 + k = 10 ⇒ k = 10 - 3
∴ k = 7
Question 17.
Krishna has an apple orchard which has a 10 m × 10 m sized kitchen garden attached to it. She divides it into a 10 × 10 grid and puts soil and manure into it. She grows a lemon plant at A, a coriander plant at B, an onion plant at C and a tomato plant at D. Her husband Ram praised her kitchen garden and points out that on joining A, B, C, D they may form a parallelogram. Look at the below figure carefully and answer the following questions:
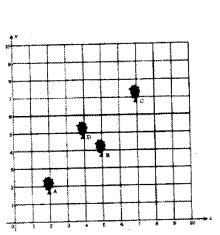
i) Write the coordinates of the points A, B, C and D, using the 10 × 10 grid as coordinate axes.
ii) Find whether ABCD is a parallelogram or not.
Solution:
i) Let A(2, 2), B(5, 4), C(7, 7), D(4, 5)

All sides equal, diagonals not equal.
∴ ABCD is a rhombus.
∴ ABCD is a parallelogram.
Question 18.
Find the ratio in which the line segment joining the points A(6, 3) and B(-2, -5) is divided by X-axis.
Solution:
Let the points A(6, 3), B (-2, -5)
(x1, y1) (x2, y2)
AB is divided by X-axis
The y-coordinate of that point is 0
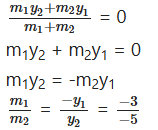
m1 : m2 = 3 : 5
∴ Required ratio = 3 : 5
Question 19.
Show that the points A(1, 7), B(4, 2), C(-1, -1) and D(-4, 4) are vertices of the square ABCD.
Solution:
Let A(1, 7), B(4, 2), C(-1, -1), D(-4, 4)

All sides are equal
AB = BC = CD = AD
Two diagonals are equal.
AC = BD
∴ ABCD is a square.
Question 20.
Prove that the points A(-1, 0), B(3, 1), C(2, 2) and D(-2, 1) are the vertices of a parallelogram ABCD. Is it also a rectangle ?
Solution:
Let A(-1, 0), B(3, 1), C(2, 2) and D(-2, 1).
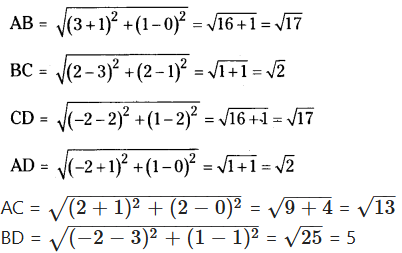
Appropriate sides are equal and diagonals are not equal.
∴ ABCD is only a parallelogram.
Question 21.
Find the co-ordinate of the points of trisection of the line-segment joining the points (5, 3) and (4, 5).
Solution:
Given points A(5, 3), B(4, 5)
(x1, y1) (x2, y2)
In points of section the ratio will be 1 : 2 (or) 2 : 1
1 : 2 = m1 : m2

Question 22.
In what ratio does the X-axis divide the line segment joining the points (-4, -6) and (-1, 7) ? Find the coordinates of the point of division.
Solution:
Given points A(-4, -6) and B(-1, 7)
(x1, y1) (x2, y2)
X-axis divides AB
Let the ratio = m1 : m2
The y-coordinate of that point is 0
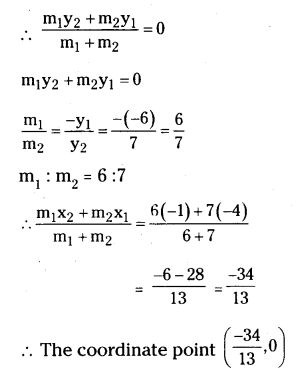
Question 23.
The vertices of a triangle are A(-1, 3), B(1, -1) and C(5, 1). Find the length of the median through the vertex.
Solution:

∴ Length of median from vertex C is 5 units.
Question 24.
Read the following passage and answer the questions that follows: In a classroom, four students. Sita, Gita, Rita and Anita are sitting at A(3, 4), B(6, 7), C(9, 4), D(6, 1) respectively, then a new student Anjali joins the class.
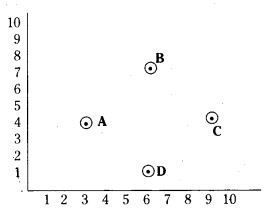
i) Teacher tells Anjali to sit in the middle of the four students. Find the coordinates of the position where she can sit.
ii) Calculate the distance between Sita and Anitha
iif) Which two students are equidistant from Gita ?
Solution:
i) Let A(3, 4), B(6, 7), C(9, 4), D(6, 1)
Midpoint of AC = (3+9/2, 4+4/2)
= (12/2, 8/2) = (6, 4)
ii) Sita A(3, 4), Anita D (6, 1)
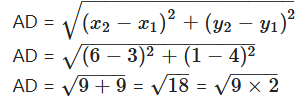
= 3√2 units
iii) Sita and Rita.
Question 25.
If the point C(-l, 2) divides internally the line segment joining the points A(2, 5) and B(x, y) is the ratio 3 : 4 find the value of x2 + y2.
Solution:

Question 26.
If the coordinate of the points A and B are (-2, -2) and (2, -4) respectively, find the coordinates of P such that AP = 3/7 AB. Where P lies on the line segment AB.
Solution:

Question 27.
Find the value of k, for which the points (7, 2), (5, 1) and (3, k) are collinear.
Solution:
The area of the triangle formed by those points = 0
Area of the triangle
1/2 {x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)} = 0
1/2|7(1 - k) + 5(k - 2) + 3(2 - 1)| = 0
1/2|-2k) = 0 .-. k = 0
Question 28.
If the distance between two points (x, 1) and (-1, 5) is ‘5’, find the value of V.
Solution:
Given points (x, 1) and (-1, 5)
Let A (x, 1) and B (-1, 5)
Distance between
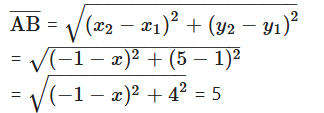
Now, squaring on both sides
(-1 - x)2 + 16 = 25
(-1 - x)2 = 25 - 16 = 9
(-1 - x)2 = 32 ⇒ -1 - x = 3
-1 - 3 = x ⇒ x = -4
Question 29.
Verify whether the following points are collinear or not.
(1, -1), (4, 1), (-2, -3)
Solution:
To show that three points are collinear the area formed by the triangle is zero. Given points are (1, -1), (4, 1), (-2, -3) Formula for area of triangle
∆ = 1/2|x1(y2 - y3) + x2(y3 - y1) + x3 (y1 - y2)|
= 1/2|1(1 + 3) + 4(- 3 + 1) - 2(- 1 - 1)|
= 1/2|8 - 8|
= 1/2|0| = 0
So the given three points are collinear.
Question 30.
Find out whether the points (1, 5), (2, 5) and (-2, -1) are collinear using the distance formula.
Solution:
A(1, 5), B(2, 5), C(-2, -1)
Distance formula,
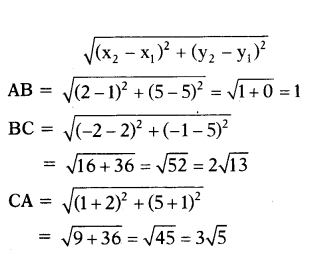
Question 31.
Find the value of k for which the points A (1, 2), B (-1, k), C (-3, -4) are collinear.
Solution:
Given A(1, 2), B(-1, k), C(-3, -4) are collinear.
∴ Area of ∆ABC = 0
⇒ 1/2|x1(y2 - y3) + x2(y3 - y1) + x3 (y1 - y2)| = o
⇒ 1/2|1[k - (- 4) + (-1)[- 4 - 2] (- 3) [2 - k] | = 0
⇒ 1/2|k + 4 + 6 - 6 + 3k| = 0
⇒ 1/2|4k + 4| = 0 ⇒ 4k + 4 = 0
⇒ 4k = -4 ⇒ k = -4/4 = - 1
(OR)
If A, B, C are collinear, then Slope of AB = Slope of BC
Now Slope of AB = y2-y1/x2-x1 = k-2/-2
Slope of AC = -4-2/-3-1 = -6/-4 = 3/2
So k-2/-2 = 3/2 ⇒ 2k - 4 = -6
⇒ 2k = - 2 .-. k = - 1
Question 32.
Show that the points A = (4, 2), B (7, 5) and C(9, 7) are collinear.
Solution:
To show that three points are collinear the area formed by the triangle is zero. Area of triangle
∆ = 1/2|x1(y2 - y3) + x2(y3 - y1) + x3 (y1 - y2)|
Here x1 = 4, y1 = 2, x2 = 7, y2 = 5, x3 = 9, y3 = 7
Now ∆ = 1/2|4(5 - 7) + 7(7 - 2) + 9(2 - 5)|
= 1/2|4(- 2) + 7(5) + 9 (-3)|
= 1/2|- 8 + 35 - 27|
= 1/2|0| = 0
So the above three are collinear.
Question 33.
If the distance between die two points (8, x) and (x, 8) is 2√2 units, then find the value of ‘x’.
Solution:
Given points are (8, x) and (x, 8) distance between them is 2√2 units.
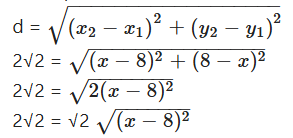
⇒ ± 2 = x - 8
x - 8 = 2 or x - 8 = -2
⇒ x = 10 or x = 6
Question 34.
Find the coordinates of point which divides the segment joining (2, 3) and (- 4, 0) in 1 : 2.
Solution:
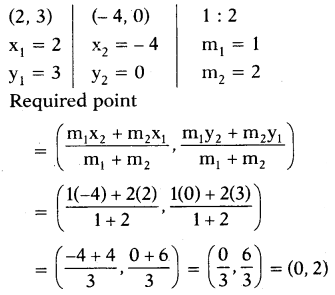
10th Class Maths Coordinate Geometry 8 Marks Important Questions
Question 1.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2, -5) and R(-3, 6), then find the coordinates of P.
Solution:
Let the point P(x, y) be the point equidistant from Q(2, -5) and R(-3, 6) and
given x = 2y. That is PQ = PR
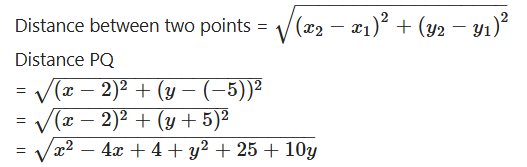

2y + 29 = 45
2y = 45 - 29
2y = 16
y = 16/2 = 8
x = 2y = 2 × 8 = 16
Therefore P(x, y) = (16, 8)
Question 2.
Show that four points (0, -1), (6, 7), (-2, 3) and (8, 3) are the vertices of a rectangle also find its area.
Solution:
Let A(0, -1), B(6, 7), C(-2, 3) and D(8, 3) be the given points.
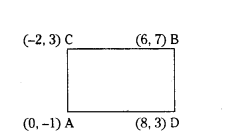


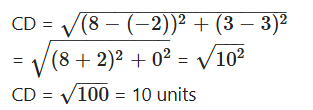
AB = CD = 10 units
In the given quadrilateral AD = BC, BD = AC and diagonals AB = CD.
So, ADBC is a rectangle.
Area of the rectangle = AD × AC = 4√5 × 2√5
Therefore area of the rectangle = 8 × 5 = 40 sq. units
Question 3.
If the vertices of an equilateral triangle (0,0), (3, √3), find the third vertex.
Solution:
Let O(0, 0), A(3, √3 ) and B(x, y) be the vertices of an equilateral triangle OAB.
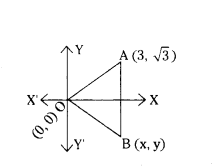
That is OA = OB = AB.
OA2 = OB2 = AB2
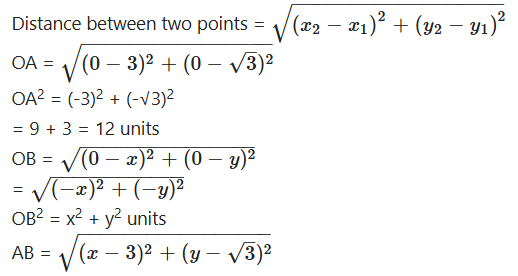
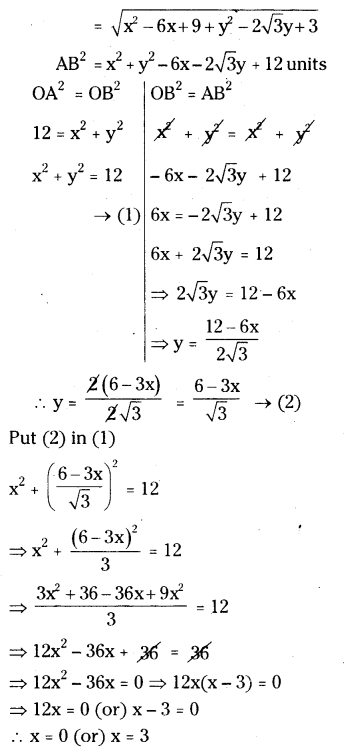
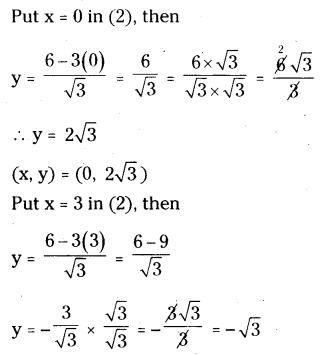
(x, y) = (3, - √3)
Therefore, the third vertex B are (0, 2√3) or(3,- √3).
Question 4.
Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of square ABCD.
Solution:
Given A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of quadrilateral ABCD.

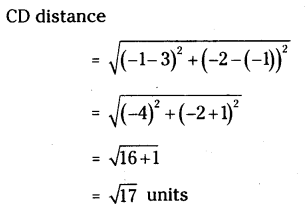

If in a quadrilateral all sides are equal and diagonals are equal, then it is said to be square.
Therefore, ABCD is a square.
Question 5.
Prove that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right angled triangle.
Solution:
Let A(7, 10), B(-2, 5), C(3, -4) are the vertices of ∆ABC.
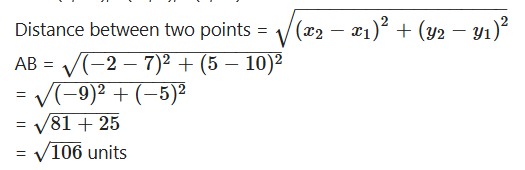

AB2 + BC2 = (√106)2 + (√106)2 = 106 + 106 = 212
AB2 + BC2 = AC2
So, given points are vertices of an isos-celes right angled triangle.
Question 6.
Point X divides the line segment joining the points A(-1, 3) and B(9, 8) such that AD/DB = k/l. If x lies on the line x - y + 2 = 0, find the value of k.
Solution:
Let X(x, y) divides the line segment joining the points A(-1, 3) and B(9, 8) in the ratio AX : BX = k : 1 and X(x, y) lies on x - y + 2 = 0 Section formula = (m1x2+m2x1/m1+m2, m1y2+m2y1/m1+m2)
x1 = -1, y1 = 3; x2 = 9, y2 = 8;
m1 = k, m2 = 1
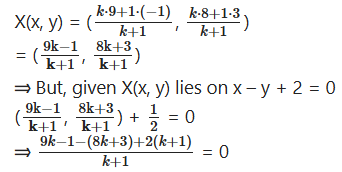
⇒ 9k - 1 - 8k - 3 + 2k + 2 = 0
⇒ 11k - 8k - 4 + 2 = 0
⇒ 3k - 2 = 0 => k = 2/3
⇒ k : 1 = - : 1 = 2 : 3
AX : BX = k : 1 = 2 : 3
Therefore, dividing ratio is 2 : 3.
Question 7.
Find the ratio in which the line segmentjoining (-2, -3) and (5,6) divided by i) x-axis ii) y-axis.
Also find the coordinates of the point of division in each case.
Solution:
i) Let P(x, 0) is the point on x-axis which divides the line joining the points A(-2, -3) and B(5, 6) in the ratio m1 : m2

By comparing x and y coordinates
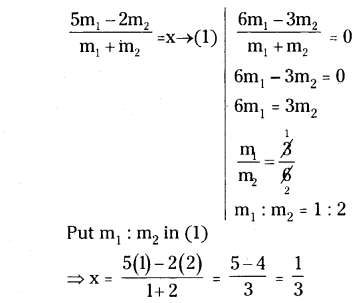
Therefore, P(x, 0) = P(1/3, 0) divides in the ratio 1 : 2 internally,
ii) Let Q(0, y) is the point on y-axis which divides the line joining the points A(-2, -3) and B(5, 6) in the ratio m1 : m2
x1 = -2
x2 = 5,
y1 = -3
y2 = 6
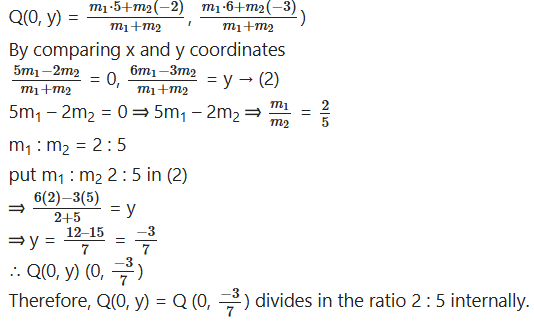
Question 8.
If the coordinates of the mid-points of the sides of a triangle are (3, 4), (4, 6) and (5, 7), find the vertices.
Solution:
Let A(x1, y1), B(x2, y2) and C(x3, y3) are the vertices of ∆ABC.

y1 + y2 = 8 → (1)

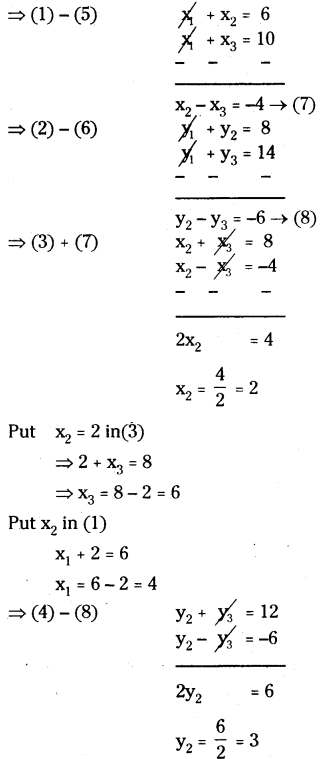
Put y2 = 3 in (4)
⇒ 3 + y3 = 12
⇒ y3 = 12 - 3 = 9
Put y2 = 3 in (2)
⇒ y1 + 3 = 8
⇒ y1 = 8 - 3 = 5
A(x1, y1) = (4, 5)
B(x2, y2 = (2, 3)
C(x3, y3) = (6, 9) are the vertices of ∆ABC.
Question 9.
The line segment joining the points (3, -4) and (1, 2) is trisected at the points X and Y. If the coordinates of X and Y are (p, -2) and (5/3, q) respectively. Find the value of p and q.
Solution:
Let A(3, -4) and B(1, 2) are the points of line segment AB.
Given X(p, -2) and Y (5/3, q) are the trisecting points which divides in the ratio X is 2 : 1 and Y is 1 : 2.
Section formula = (m1x2+m2x1/m1+m2, m1y2+m2y1/m1+m2)
Trisecting point X(p, -2) can divide A(3, -4) and B(1, 2) in the ratio 1 : 2
x1 = 3, y1 = -4, m1 = 1
x2 = 1, y2 = 2, m2 = 2
X = (1/1+2.3/1+2, 1?2+2(-4)1/+2) = (p, -2)
⇒ (1+6/3, 2-8/3) = (p, -2)
By comparing x, y coordinates 7/3 = p
Trisecting point Y (5/3, q) can divide
A(3, -4) and B(1, 2) in the ratio 2 : 1
x1 = 3, y1 = -4, m1 = 2
x2 = 1, y2 = 2, m2 = 1
Y = (2.1+1.3/2+1, 2?2+1(-4)2/+1) = (53/, q)
⇒ (2+3/3, 4-4/3) = (5/3, q)
⇒ (5/3, 0) = (5/3, q)
By comparing x and y-coordinates q = 0.
Therefore p = 7/3 and q = 0.
Question 10.
Find the points of trisection of the line segment joining the points A(5, -6) and B(-7, 5).
Solution:
Given AB is the line joining the points A(5, -6) and B(-7, 5).
Trisecting point: A point which divides the line joining by the points in the ra¬tio 1:2 (or) 2:1 is called trisecting point.
Let P divides 1 : 2 and Q divides AB are the trisecting points.
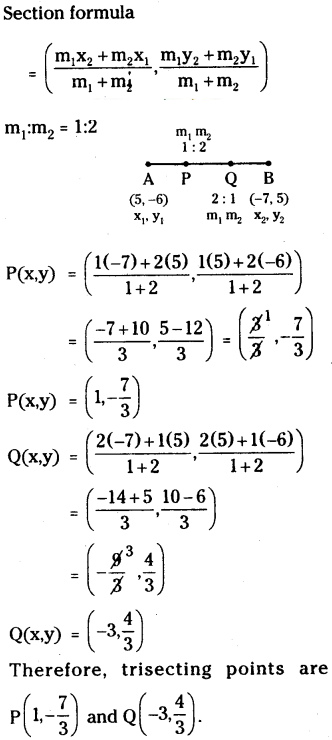
Q (x, y) = (-3, 4/3)
Therefore, trisecting points are P (1, 7/3) AND (-3, 4/3)
Question 11.
If the points A(6, 1), B(8, 2), C(9, 4) and D(x, y) are the vertices of a parallelogram taken in order, then find the value of x and y.
Solution:
Given A(6, 1), B(8, 2), C(9, 4) and D(x, y) are the vertices of parallelogram ABCD.
In parallelogram diagonals bisect each other that is mid points of diagonals are same.
So, midpoint of diagonal BD = midpoint of diagonal AC

Therefore, fourth vertex D(x, y) = (7, 3).
Question 12.
In what ratio does the point (-4, 6) divide the line segment joining the points A(-6, 10) and B(3, -8) ?
Solution:
Let P(-4, 6) can divide the line joining by the points A(-6, 10) and B(3, -8) in the ratio m1 : m2.

3m1 - 6m2 = - 4(m1 + m2)
3m1 - 6m2 = - 4m1 - 4m2
3m1 + 4m1 = - 4m2 + 6m2
7m1 = 2m2
m1/m2 = 1/2
m1 : m2 = 2 : 7
Therefore, ratio = 2 : 7
Question 13.
Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution:
Let P(x, y); A(7, 1); B(3, 5)
The distance between points (x1, y1) and (x2, y2) is

50 - 14x + x2 - 2y + y2 = 34 - 6x + x2 - 10y + y2
50- 14x - 2y - 34 + 6x + 10y = 0
-8x + 8y + 16 = 0
-x + y + 2 = 0
∴ x = y + 2
Question 14.
If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a parallelogram, taken in order, then
i) find the value of p.
ii) find the area of ▭ ABCD.
Solution:
i) A, B, C, D are the vertices of a parallelogram
Mid point of AC = Mid point of BD

ii) ar ∆ABC = 1/2 |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)
= 1/2 |6(2 - 4) + 8(4 - 1) + 9(1 - 2)|
= 1/2 |-12 + 24 - 9|
= 1/2 |3|=3/2 sq. units.
∴ Area of parallelogram ABCD
= 2 × ar ∆ABC
= 2 × ar ∆ABC = 2 × 1/2
= 3 sq. units.
Question 15.
Find the value of ‘k’ for which the points (3k - 1, k - 2), (k, k - 7) and (k - 1, -k -2) are collinear.
Solution:
Given points are collinear
Let A (3k - 1, k - 2), B (k, k - 7) and C (k- 1, -k -2) are on the same line ABC.
Then slope of AB and slope of AC should be same (∵ they are collinear)
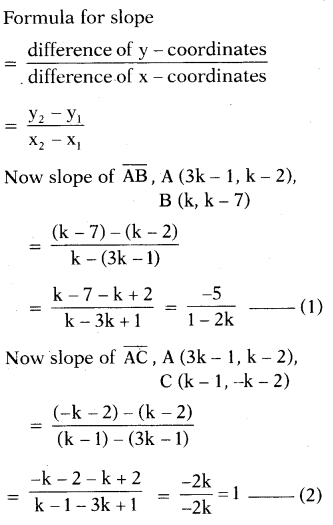
Now (1) = (2)
⇒ -5/1-2k = 1 ⇒ 1 - 2k = -5
⇒ 1 + 5 = 2k
⇒ 2k = 6
∴ k = 3
Question 16.
Find the co-ordinates of the points of trisection of the line segment joining the points A(2, 1) and B(5, - 8).
Solution:
Let P and Q be the points of trisection of AB, i.e.f AP = PQ = QB.
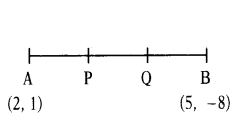
Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordi¬nates of P are (by applying the section formula)
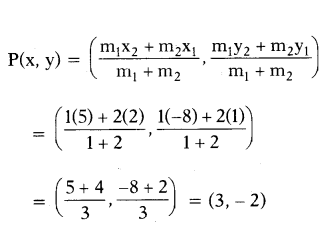
Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are
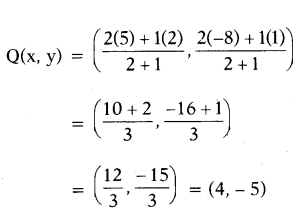
There fore, the coordinates of the points of trisection of the line segment are P(3, - 2) and Q(4, - 5).
Question 17.
If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, then find the area of the quadrilateral ABCD.
Solution:
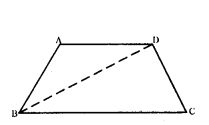
By joining B to D, you will get two triangles ABD and BCD.
The area of ∆ABD
= 1/2 |- 5 (- 5 - 5) + (- 4) (5 - 7) + 4 (7 + 5)|
= 1/2 |50 + 8 + 48| = 106/2 = 53 sq. units.
Also, the area of ∆BCD
= 1/2 |- 4 (- 6 - 5) - 1 (5 + 5) + 4 (- 5 + 6)|
= 1/2 |44 - 10 + 41 = 19 sq. units.
So, the area of quadrilateral
= Area of ∆ABD + Area of ∆BCD
= 53 + 19 = 72 sq. units.
Question 18.
Find the trisection points of the line segment joined by the points (-3, 3) and (3, -3).
Solution:
The points which divide the line segment by 1 : 2 and 2 : 1 ratio (internally) are called trisection points.
Formula for the points of trisection of the line segment joined by (x1, y1) and (x2, y2) are
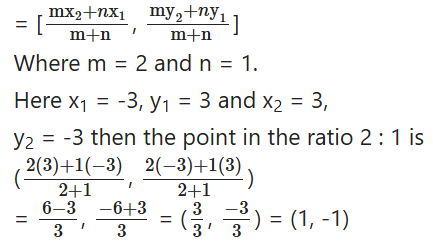
So (1, -1) is one trisection point. The point which is at 1 : 2 ratio is another trisection point.
So m = 1, n = 2, x1 = -3, y1 = 3, x2 = 3 and y2 = -3
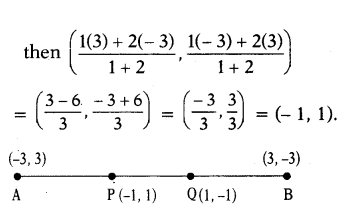
P, Q are trisection points.
Question 19.
If the points P(-3, 9), Q(a, b) and R(4, -5) are collinear and a + b = 1, then find the values of a and b.
Solution:
Points P, Q, R are colliner ⇒ area of ∆PQR = 0
P(-3, 9), Q(a, b), R(4, - 5)
Area of triangle
= 1/2 |-3(b + 5) + a(- 5 - 9) + 4(9 - b)|
after simplifications,
we get 2a + b = 3 ______ (1)
given equation a + b = 1 ______ (2)
Solving equations (1) and (2), we obtain
a = 2 and b = - 1
Question 20.
The area of the triangle is 18 sq. units, whose vertices are (3, 4), (-3, -2) and (p, -1); then find the value of ‘p’.
Solution:
Given points are (3, 4) (-3, -2) (p, -1)
x1 = 3, y1 = 4, x2 = -3, y2 = -2, x3 = p, y3 = -1
Area of triangle = 1/2 |x1(y2 - y3) + x2(y3 - y1) + x3(y1 - y2)
18 = 1/2 |(3 (-2 + 1) - 3 (- 1 - 4) + p(4 + 2)|
⇒ |- 3 + 15 + 6p| = 36
⇒ 6p + 12 = 36 (or) 6p + 12 = -36
P = 36-12/6 , P = -36/-12
P = 24/6 = 4, P = -48/6 = -8
∴ P = 4 or -8
Question 21.
Find the points of tri-section of the line segment joining the points (-2, 1) and
a 4). 1
Solution:
Given points (-2, 1) (7, 4)
x1 = - 2
y1 = 1
x2 = 7
y2 = 4
Points of trisection means the points which divide it in the ratio 1 : 2 and 2 : 1

= (4, 3)
∴ Points of trisection are (1,2) and (4, 3).
Question 22.
Find the ratio in which X-axis divides the line segment joining the points (2, - 3) and (5, 6). Then find the intersecting point on X-axis.
Solution:
Let X - axis divides the line segment joining points
(2, - 3) and (5, 6) in the ratio m1 : m2
x1 = 2
y1 = -3
x2 = 5
y2 = 6
Co-ordinate of point
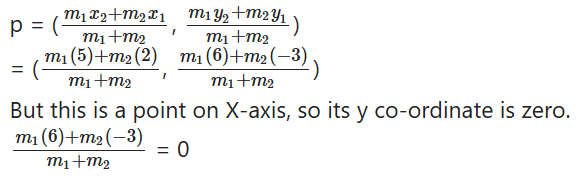
6m1 - 3m2 = 0
6m1 = 3m2 ⇒ m1/m2 = 3/6 = 1/2
∴ Required ratio = 1 : 2
point P on X - axis = (1(5)+2(2)/1+2, 0)
= (9/3, 0) = (3, 0)
Question 23.
Show that the points A(-1, -2), B(4, 3), C(2, 5) and D(-3, 0) in that order form a rectangle.
Solution:
Given points are A (-1, -2), B (4, 3)
C (2, 5), D (-3, 0)
Mid point of AC = (-1+2/2, -2+5/2)
= (1/2, 3/2)

Diagonal are equal and bisect each other. So given vertices form a rectangle.
Question 24.
Find the area of a rhombus ABCD, whose vertices taken in order, are A (-1, 1), B(1, -2), C(3, 1) andD(1, 4).
Solution:
Area of a rhombus = 1/2 × (Product of its diagonals)
Let the vertices be = 1/2 × AC × BD
A (-1, 1), B(1, -2), C(3, 1), D (1, 4)
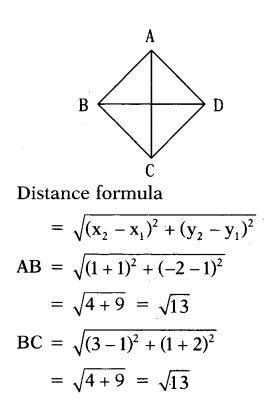

∴ Area of Rhombus = 1/2 × d1 × d2
= 1/2 × 4 × 6
= 12 sq. units.
Question 25.
If A(-2, 2), B(a, 6), C(4, b) and D(2( -2) are the vertices of a parallelogram ABCD, then find the values of a and b. Also find the lengths of its sides.
Solution:
Vertices of parallelogram ABCD are
A(-2, 2), B(a, 6), C(4, b), D(2, -2)
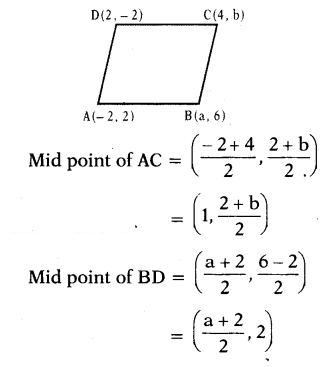
Since it is a parallelogram, mid-points of diagonals coincide.
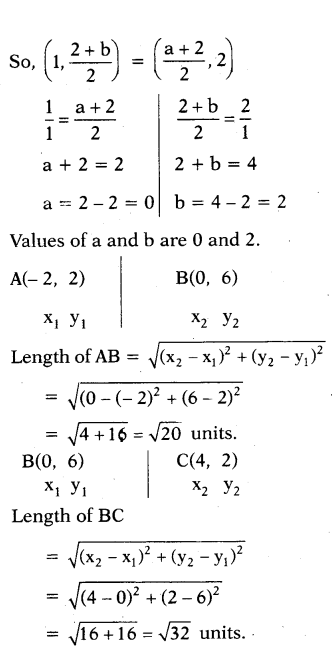
AB = DC = √20 [∵ opposite sides of a parallelogram are equal ]
AD = BC = √32
Question 26.
The three vertices of a parallelogram ABCD are A(-1, -2), B(4, -1) and C (6, 3). Find the coordinates of vertex D and find the area of parallelogram ABCD.
Solution:
Mid point of AC
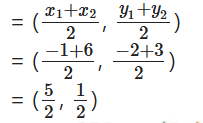

= 1/2| (-1) (- 1 - 2) + 4[2 - (- 2)] + 1[- 2 -(- 1)]|
= 1/2|(-1) (-3) + 4 (4) + 1(-1)|
= 1/2|3 + 16 - 1|
= 1/2 × 18
= 9 Square units
Area of parallelogram ABCD
= 2 × ∆ ABD area
= 2 × 9
= 18 Square Units
AP 10th Class Maths 7th Lesson Important Questions and Answers Coordinate Geometry
Question 1.
What do you mean by centroid of a triangle ?
Solution:
"The concurrent point of medians of a triangle is called centroid of the triangle".
Question 2.
Find the co-ordinates of the point, which divides the line segment joining (2, 0) and (0, 2) in the ratio 1:1.
Solution:
x1 = 2 ; x2 = 0 ; y1 = 0 ; y2 = 2
Point divides the line segment joining (2,0) and (0, 2) in the ratio 1 : 1
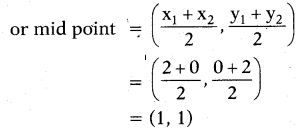
Question 3.
Find the distance between (a cos θ, 0) and (0, a sin θ).
Solution:
To find the distance between the points (a cos θ, 0) and (0, a sin θ) we use the formula.
√(x1-x2)2+(y1-y2)2
Where x1 = 0, y1 = a sin θ and
x2 = a cos θ, y2 = 0
∴ The distance between above given two points
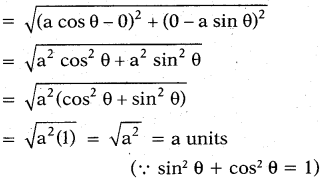
Question 4.
If A(4,0), B(0, y) and AB = 5, find the possible values of y. d
Solution:
A(4,0), B(0, y) and AB = 5
= 5
= 5
16 + y2 = 2
y2 = 25 - 16 = 9
y = ± √9 = ± 3
Possible values of y are 3 or - 3.
Question 5.
Find the radius of the circle with cen¬tre (3, 2) and passes through (4, - 1).
Solution:

Question 6.
Let the 3 vertices of a triangle ABC are A(3, -2), B(-5, 4) and C(2, - 2). What do you observe for the centroid of this triangle ?
Solution:
centroid of this triangle
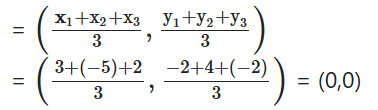
Observed that the centroid is the origin.
Question 7.
Find the centroid of a triangle, whose vertices are (6, 2), (0, 0) and (4, -5).
Solution:
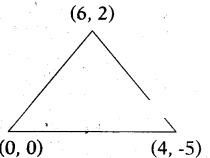
Given vertices are (6, 2) (0, 0) and (4, -5) then centroid
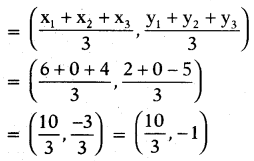
Question 8.
Find the radius of the circle whose cen-tre is (3, 2) and passes through (- 5, 6).
Solution:
Given : A circle with centre A (3, 2) passing through B (- 5, 6).
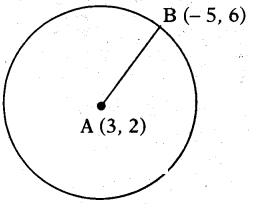
Radius = AB
[ ∵ Distance of a point from the centre of the circle]
Distance formula
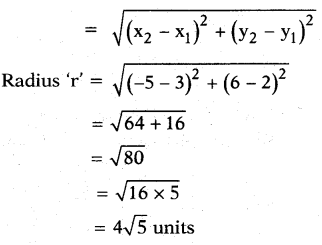
Question 9.
What is the distance between (0, - sin x) and (- cos x, 0) ?
Solution:
Distance between (0, - sin x) and (- cos x, 0)
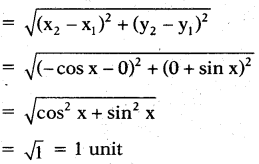
Question 10.
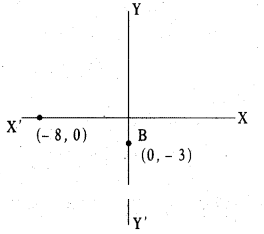
Where do the points (0, -3) and (-8, 0) lie on co-ordinate axis ?
Solution:
The point (0, - 3) lie on OY
∵ Its x co-ordiante is zero and
y - coordinate is negative.
and the point (-8, 0) lie on OX’
∵ Its y - cordinate is zero and
x-cordinate is negative.
Question 11.
Find a relation between x and y such that the point (x, y) is equidistant from the points (7, 1) and (3, 5).
Solution:
Let P(x, y); A(7, 1); B(3, 5)
The distance between points (x1, y1) and (x2, y2) is
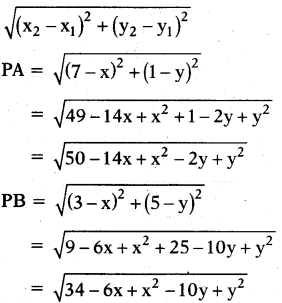
by the sum, PA = PB
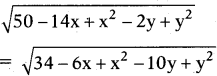
50 - 14x + x2 - 2y + y2
= 34 - 6x + x2 - 10y + y2
50 - 14x - 2y - 34 + 6x 4- 10y = 0
-8x + 8y + 16 = 0
-x + y + 2 = 0 ,
∴ x = y + 2
Question 12.
Find the value of k, for which the points (7, 2), (5, 1) and (3, k) are collinear.
Solution:
The area of the triangle formed by those points = 0
Area of the triangle
1/2 {x1(y2-y3) + x2(y3-y1)
+ x3(y1 - y2)} = 0
1/2 |7(1 - k) + 5(k - 2) + 3(2 - 1)| = 0
1/2 |-2k| = 0
∴ k = 0
Question 13.
Find the centroid of the triangle, whose vertices are (-4, 4), (-2, 2) and (6,-6).
Solution:
Centroid of the triangle
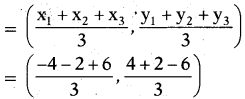
= (0,0)
Question 14.
If the distance between two points (x, 1) and (-1,5) is ‘5’, find the value of V.
Solution:
Given points (x, 1) and (-1, 5)
Let A (x, 1) and B (-1, 5)
Distance between
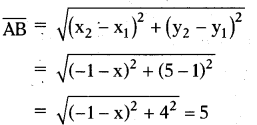
Now, squaring on both sides (-1 -x)2 + 16 = 25
(-1 - x)2 = 25- 16 = 9
(-1 - x)2 = 32
-1 - x = 3
-1 - 3 = x ⇒ x = -4
Question 15.
Verify whether the following points are collinear or not.
(1,-1), (4, 1), (-2,-3)
Solution:
To show that three points are collinear the area formed by the triangle is zero.
Given points are (1, -1), (4, 1), (-2, -3) Formula for area of triangle
A = 1/2 {x1(y2-y3) + x2(y3-y1)
= 1/2 |1(1 +3) + 4(-3 + 1)
-2 (-1-1)1
= 1/2|4-8 + 4|.
= 1/2|0| = 0
So the given three points are collinear.
Question 16.
Find the area of a triangle, whose sides are 5 cm, 12 cm and 13 cni, by using Heron’s formula.
Solution:
Let a = 5 cm; b = 12 cm; :c =13 cm
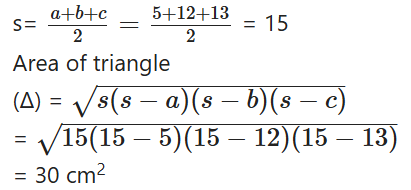
Question 17.
Find out whether the points (1,5), (2, 5) and (-2,-1) are collinear using the distance formula.
Solution:
A(1, 5), B(2, 5), C(- 2,-1)
Distance formula,
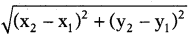
Question 18.
Read the following graph and answer the questions given below.
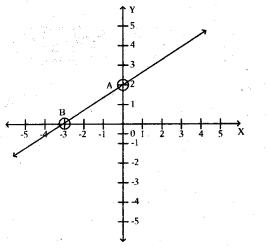
i) Write the coordinates of the points A and B.
ii) What is the slope of the line AB ?
Solution:
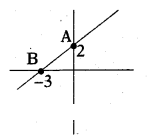
i) Coordinates of
point ‘A’ = (0, 2)
point B = (-3, 0)
ii) Slope = y2-y1/x2-x1
= 0-2/-3-0 = -2/-3 = 2/3
Question 19.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, - 3) and B is (1, 4).
Solution:
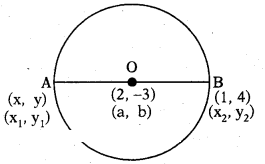

Question 20.
Check whether the points (3, 0), (6,4) and (-1, 3) are the vertices of a right - angled isosceles triangle or not. Also find the area of the triangle.
Solution:
Distance between A(3, O), B(6, 4)
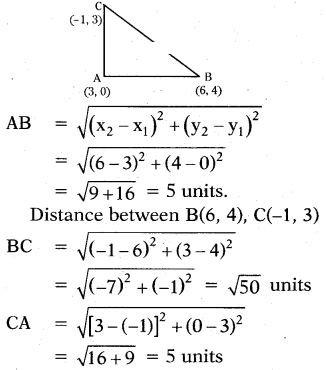
∴ AB2 = 25, BC2 = 50, CA2= 25
BC2 = AB2 + CA2 and AB = CA
∴ ∆ ABC is an Isosceles right angled triangle
∴ Area of ∆ABC = 1/2 x AB x AC
= 1/2 x 5 x 5 = 12.5sq.u
Question 21.
Find the area of the triangle formed by the points (2, 3), (- 1, 3)and (2,-1) using Heron’s formula.
Solution:
To find the area of the triangle formed by (2, 3) (- 1, 3) and (2,-1) using Heron’s formula.
Let the co-ordinates of A = (2, 3) ; B = (- 1, 3); C = (2, - 1) then the sides of AABC are represented by as follows

∴ CB = a = distance between the points (2, - 1) and (-1,3)
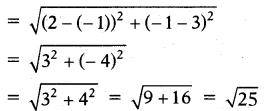
⇒ CB = a = 5 ........(1) .
and AB = c the distance between (-1,3) and (2, 3)
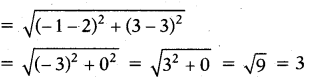
∴ AB = c = 3 .........(2)
and AC = b the distance between A(2, 3) and C(2, - 1)
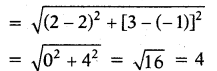
AC = b = 4 ......(3)
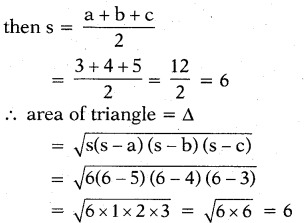
∴ Area of above triangle = 6 sq.units.
Question 22.
If the points A(6, 1), B(8, 2), C(9, 4) and D(p, 3) are the vertices of a paral-lelogram, taken in order, then
i) find the value of p.
ii) find the area of ▭ABCD.
Solution:
i) A, B, C, D are the vertices of a parallelogram
Mid point of AC =- Mid point of BD
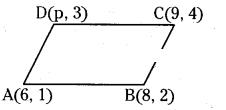
A(6, 1) = (x1, y1); C(9, 4) - (x2, y2)

ii) ar ∆ABC = 1/2 | x1 (y2 - y3) + x2(y3 - y1)
+ x3 (y1 -y2)|
= 1/2|6(2 - 4) + 8(4 - 1) + 9(1 - 2)|
= 1/2 |-12+24-9|
= 1/2 |3
= 3/2|sq. units.
∴ Area of parallelogram ABCD = 2 x ar AABC 3
= 2 × 3/2 = 3 sq. units.
Question 23.
Find the value of ‘k’ for which the points (3k - 1, k - 2), (k, k - 7) and (k - 1, -k -2) are collinear.
Solution:
Given points are collinear
Let A (3k - 1, k - 2), B (k, k - 7) and
C (k - 1, -k - 2) are on the same line LN
Then slope of AB and slope of AC should be same (∵ they are collinear) Formula for slope
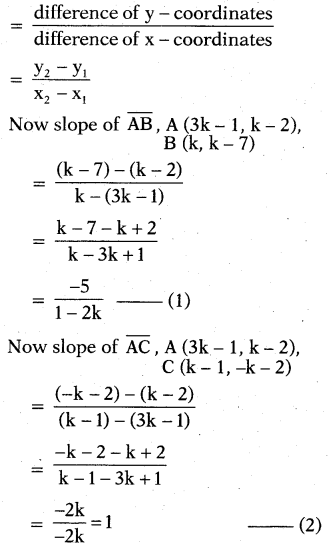
Now (1) = (2)
⇒ ?5/1?2k = 1
⇒ 1 - 2k = -5
⇒ 1 + 5 = 2k ⇒ 2k = 6
∴ k = 3
Question 24.
Find the co-ordinates of the points of trisection of the line segment joining the points A(2, 1) and B(5, - 8).
Solution:
Let P and Q be the points of trisection of AB, i.e., AP = PQ = QB.
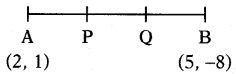
Therefore, P divides AB internally in the ratio 1 : 2. Therefore, the coordi¬nates of P are (by applying the section formula)
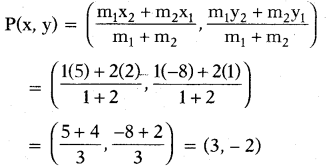
Now, Q also divides AB internally in the ratio 2 : 1. So, the coordinates of Q are
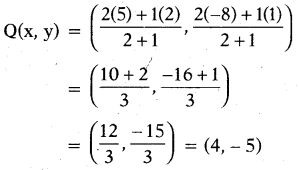
Therefore, the coordinates of the points of trisection of the line segment are P(3, - 2) and Q(4, - 5).
Question 25.
Find the distance between the points (5, 7) and (7, 5).
Solution:
Formula for the distance between the points (x1, y1) and (x2, y2) is √(x2?x1)2+(y2?y1)2
Here (x1, y1)=(5,7) and (x2, y2) = (7, 5)
∴ The distance between (5, 7) and (7, 5) is
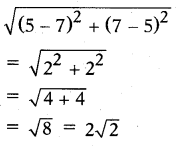
Question 26.
Find the distance between the points (5, 7) and (7, 5) by plotting them in co-ordinate plane with the help of a right angled triangle.
Solution:
A (5, 7), B (7, 5) then O (5, 5)
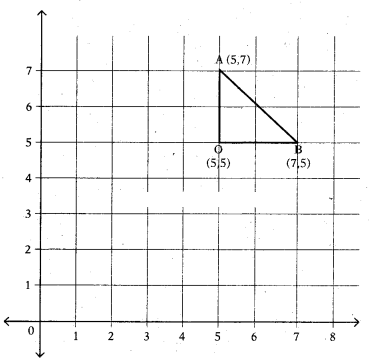
In the ∆AOB, ∠O = 90
∴ AB is hypotenuse.
AO =(7 - 5)= 2
OB = 7 - 5 = 2
Then from Pythagorus theorem
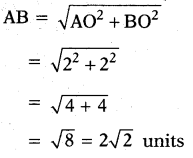
Hence the distance between (5, 7) and (7, 5) = 2√2 units
Question 27.
Are the points (5, 7) and (7, 5) equal ?
Solution:
No, the given points (5, 7) and (7, 5) are not equal.
Why because, the above two points represent two different points in the co-ordinate plane.
So they are not equal.
For (x1, y1) = (x2, y1) then x1 must be equal to x2 and y1 must be equal to y2.
So to become (5, 7) = (7, 5)
5 should be equal to 7, which is impossible.
So (5, 7) will not bp equal to (7, 5).
Question 28.
Find the point on X-axis which is equi distant from the points (5, 7) and (7,5).
Solution:
Let the point (p, q) i$ on X-axis, which is equi distant from the points (5, 7) and (7, 5).
As this point (p, q) is on X-axis, its y-coordinate q = 0. Then the point is
(p, 0).
The distance between (5, 7) and (p, 0) is √(p?5)2+(0?7)2 ..... (1)
And the distance between (7, 5) and (p,0) is √(p?7)2+(0?5)2...... (2)
The above (1) and (2) are equal.
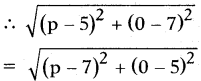
= (p - 5)2 + 72
= (p - 7)2 + 52
= p2 - 10p + 25 + 49 = p2 - 14p + 49 + 25
∴ -10p + 14p = 0
⇒ 4p = 0
∴ P = o
So (p, 0) = (0, 0) is the point on X-axis, which is equidistant from (5, 7) and (7, 5).
Question 29.
To which quadrants do the following points belong ?
(i) (5, 7)
(ii) (5, - 7)
(iii) (-5, 7)
(iv) (-5, -7)
Solution:
(5, 7) belongs to first quadrant q1
(5, -7) belongs to fourth quadrant q4.
(-5, 7) belongs to second quadrant q2.
(-5, -7) belongs to third quadrant q3.
Question 30.
What will be the lengths of line seg-ments that are parallel to X-axis, as shown in figure ?
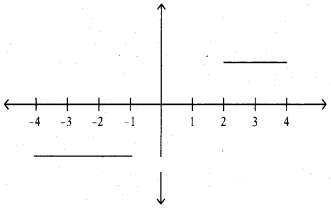
Solution:
In the above figure, length of the line segment above the X-axis is 4 - 2 = 2
And length of line segment below X-axis is 4 - 1 = 3