5th Lesson Arithmetic Progressions Class 10 Important Questions with Solutions
10th Class Maths Arithmetic Progressions 1 Mark Important Questions
Question 1.
Write the nth term of A.P.
Solution:
an = a + (n - 1) d
a = first term,
d = common difference,
n = number of terms.
Question 2.
Write the 5th term of an = 3n.
Solution:
Given an = 3n
put n = 5 in an = 3n
then a5 = 35 = 243
Question 3.
Write 8th term of an = 3n + 2.
Solution:
Given an = 3n + 2
Put n = 8 in an = 3n + 2
then a8 = 3(8) + 2 = 24 + 2 = 26
Question 4.
Write the first term and common difference of the following arithmetic progression.
i) -5, -1, 3, 7, . . .
ii) 1/5, 3/5, 1, 7/5, . . .
Solution:
i) Given A.P : -5, -1, 3, 7, . . .
First term a = -5
Common difference (d) = a2 - a1
= - 1 - (-5)
= -1 + 5
∴ d = 4
ii) Given 1/5, 3/5, 1, 7/5, . . .
First term a = 1/5
Common difference
∴ d = 5/5 - 3/5 = 5-3/5 = 2/5
Question 5.
Write the formula for sum of n terms in A.P.
Solution:
Sn = n/2 [2a + (n - 1) d]
n = number of terms,
a = first term,
d = common difference
Question 6.
Write the formula for sum of n terms in A.P., if a is first term and / is the last term.
Solution:
sn = n/2 (a + l)
n = number of terms,
a = first term
l = last term
Question 7.
Find the thirteen term from the last term of the AP.
20, 13, 6, -1, ... - 148.
Solution:
AP 20, 13, 6, -1 .... - 148
a = 20, d = 13 - 20 = -7.
Reversed AP -148, -141, -134 . -1, 6, 13, 20
a = -148, d = -141 + 148 = 7
a13 = a + 12d
= -148 + 12(7) = -148 + 84 = - 64
Question 8.
In an A.P. nth term is 5n - 7. Find the common difference of that series.
Solution:
an = 5n - 7
a1 = 5(1) - 7 = 5 - 7 = -2
a2 = 5(2) - 7 = 10 - 7 = 3
a3 = 5(3) - 7 = 15 - 7 = 8
AP = -2, 3, 8 ......
d = 3 - (-2) = 5
Question 9.
Find the value of ‘k’, k + 2, 4k - 6, 3k - 2 are in A.P.
Solution:
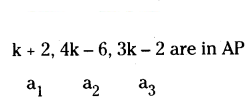 a2 - a1 - a3 - a2
a2 - a1 - a3 - a2
4k - 6 - (k + 2) = 3k - 2 - (4k - 6)
4k - 6 - k - 2 = 3k - 2 - 4k + 6
3k - 8 = -k + 4
3k + k = 8 + 4
4k = 12
k = 3
Question 10.
What is the common difference of the A.P., 1/p, 1-p/p, 1-2p/p,?
Solution:
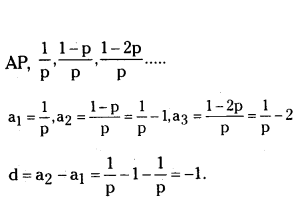
Question 11.
What is the nth term of the A.P, a, 3a, 5a, .. ?
Solution:
AP a, 3a, 5a ....
d = 3a - a = 2a
an = a + (n - 1) d
= a + (n - 1) 2a
= a + 2an - 2a
= 2an - a = a(2n - 1)
Question 12.
Find the eleventh term from the last term of the A.P.
27, 23, 19, ..., -65
Solution:
Given AP 27, 23, 19 ... 65
Reversed AP -65, -61, -57, .... 19, 23, 27.
a = -65,
d = -61 + 65 = 4
a11 = a + 10d
= -65 + 10(4)
a11 = -25
Question 13.
Find the 17th term from the end of the
A.P. : 1, 6, 11, 16,.. 211, 216
Solution:
Given AP 1, 6, 11, 16 .... 211, 216
Reversed AP 216, 211, 206, 201 .... 16, 11, 6, 1
a = 216
d = 211 - 216 = -5
a17 = a + 16(d)
= 216 + 16(-5) = 216 - 80
∴ a17 = 136.
Question 14.
Find the value of x for which 2x, (x + 10) and (3x + 2) are the three consecutive terms of an A.P., is
Solution:
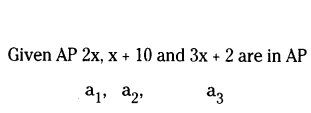 a2 - a1 = a3 - a2
a2 - a1 = a3 - a2
x + 10 - 2x = 3x + 2 - x - 10
- x + 10 = 2x - 8
- x - 2x = - 8 - 10
-3x = -18
x = 6
Question 15.
The first term of A.P. is p and the common difference is q, then find its 10th term.
Solution:
Given AP a = p, d = q
a10 = a + 9d
= p + 9q
Question 16.
The 8th term of an A.P. is 17 and its 14th term is 29. Find the common difference of this A.P.
Solution:
In an AP a8 = 17
a + 7d = 17 ... (1)
a14 = 29
a + 13d = 29 ... (2)
(2) - (1) → 6d = 12
d = 2
Question 17.
The next term of the sequence
√2, √8, √18, √32 .... is .....
Solution:
√2, √8, √18, √32 ....
√2, √4×2, √9×2, √16×2
√2, 2√2, 3√2, 4√2
The next term is = 5√2 = √5×5×2 = √50
Question 18.
If the common difference of AP is -6 then a16 - a12 = ....... .
Solution:
d = -6
a16 - a12 = a + 15d - (a + 11d)
= a + 15d - a - 11d
= 15d - 11d
= 4d = 4(-6) = -24
Question 19.
The first three terms of the AP are 3y - 1, 3y + 5 and 5y + 1 respectively then y = ....... .
Solution:
3y - 1, 3y + 5, 5y + 1 are in AP
a2 - a1 = a3 - a2
3y + 5 - (3y - 1) = 5y + 1 - (3y + 5)
3y + 5 - 3y + 1 = 5y + 1 - 3y - 5
6 = 2y - 4
2y = 10
y = 5
Question 20.
In a series, an = 17/n2+1 then a3 = .....
Solution:
an = 17/n2+1
a3 = 17/32+1 = 17/9+1 = 17/10
Question 21.
What is the sum of first 100 natural numbers?
Answer:
5050
Question 22.
Find the common difference of an arithmetic progression in which a25 - a12 = -52.
Answer:
-4
Question 23.
The ‘nth‘ term of an A.P. is
an = 3 + 2n, then find the common difference.
Answer:
2
Question 24.
Find number of terms of the A.P.
-5 + (-8) + (- 11) + ... + (-230).
Answer:
76
Question 25.
If there are ‘n’ AM’s between ‘a’ and ‘b’, then find d.
b - a
Answer:
d = b-a/n+1
Question 26.
Statement (A): Common difference of the AP : - 5, - 1, 3, 7, .... is 4.
Statement (B): Common difference of the a, a + d, a + 2d, ...... is given by d - 2nd term - 1st term.
Choose the correct answer satisfying the following statements
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 27.
Statement (A): The sum of the first ‘n’ terms of an AP is given by Sn = 3n2 - 4n.
Then its nth term an = 6n - 7.
Statement (B) : nth term of an AP, whose sum to ‘n’ terms is Sn, is given
by an = Sn - Sn - 1.
Choose the correct answer satisfying the following statements
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 28.
Statement (A) : Three consecutive terms 2k + 1, 3k + 3 and 5k - 1 from an AP, then k is equal to 6.
Statement (B) : In an AP
a, a + d, a + 2d, ... the sum to n terms of the AP be Sn =n/2 [2a + (n - 1)d].
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 29.
Which mathematical concept is used to find the total distance the gardener will cover in order to water all the trees?
Answer:
Arithmetic Progression.
Question 30.
Column - II give common difference for A.P. given column -1, match them correctly.
Column - I
A) 1, 3/2, 2, 5/2, .....
B) 1/3, 5/3, 9/3,13/2
Column - II
i) -4
ii) 0.2
iii) 4/3
iv) 1/2
Answer:
A - (iv), B - (iii)
10th Class Maths Arithmetic Progressions 2 Marks Important Questions
Question 1.
Find the arithmetic progression when first term a and common difference d.
i) a = 4, d = -3
ii) a = -1, d = 1/2
Solution:
i) Given first term a = 4,
Common difference d = -3
a2 = a + d = 4 + (-3) = 4 - 3 = 1
a3 = a + 2d = 4 + 2(-3) = 4 - 6 = -2
a4 = a + 3d = 4 + 3(-4) = 4 - 12 = -8
Therefore, A.P is 4, 1, -2, -8, .
ii) Given first term a = -1,
Common difference d = 1/2
a2 = a + d = -1 + 1/2 = - 1/2
a3 = a + 2d = -1 + 2(1/2) = -1 + 1 = 0
a4 = a + 3d = -1 + (1/2) = -1 + 3/2 = 1/2
Therefore, A.P is : -1, - 1/2, 0, 1/2, ....
Question 2.
If nth term of an A.P is 6n + 2. Find the common difference.
Solution:
Given an = 6n + 2
If n = 1, a1 = 6(1) + 2 = 6 + 2 = 8
If n = 2, a2 = 6(2) + 2 = 12 + 2 = 14
Common difference d = a2 - a1
= 14 - 8
= 6
Question 3.
Find the 5th term from the end of the A.P 17, 14,11, . , 40.
Solution:
a = +40
d = -3
a5 = a + 4d
= 40 + 4(-3)
= 40 - 12
a5 = 28
Question 4.
Find the nth term of AP 13, 8, 3, -2,.
Solution:
Given A.P:13, 8, 3, -2 ..
first term a = 13,
common difference d = a2 - a1
= 8 - 13 - 5
nth term an = a + (n - 1)d
= 13 + (n - 1)(-5)
= 13 - 5n + 5
∴ an = 18 - 5n.
Question 5.
Find the sum of the arithmetic progression : 50, 46,42, . to 10 terms.
Solution:
Given A.P : 50, 46, 42, .
first term a = 50,
common difference d a2 - a1
= 46 - 50 = -4
n = 10
Sum of n terms
Sn = n/2 (2a + (n - 1)d]
S10 = 10/2 [2(50) +(10 - 1)(-4)]
= 5[100 + 9(-4)]
= 5(100 - 36)
= 5 × 64
= 320
Therefore, S10 = 320
Question 6.
Find the common difference of the AP 4, 9, 14 .. If the first term changes to 6 and the common difference remains the same the written the new AP.
Solution:
Given AP, 4, 9, 14, .....
d = 9 - 4 = 5.
Let the first term be ‘6’
also d = 5
Then new AP
a = 6
a2 = 6 + 5 = 11
a3 = 11 + 5 = 16
a4 = 16 + 5 = 21
New AP, 6, 11, 16, 21 ...
Question 7.
The sum of first n terms of an AP is given by Sn = 2n2 + 3n. Find the sixteenth term of AP.
Solution:
In an AP Sn = 2n2 + 3n.
S1 = a1 = 2(1)2 + 3(1) = 2 + 3 = 5
S2 = 2(2)2 + 3(2) = 8 + 6 = 14
S3 = 2(3)2 + 3(3) = 18 + 9 = 27
a2 = S2 - S1 = 14 - 5 = 9.
a3 = S3 - S2 = 27 - 14 = 13.
∴ AP is 5, 9, 13 ... ,a = 5, d = 9 - 5 = 4
a16 = a + 15d = 5 + 15(4) = 5 + 60 = 65.
Question 8.
Find a and b so that the numbers a, 7, b, 23 are In A.P.
Solution:
Given AP a, 7, b, 23.
a1 = a, a2 = 7, a3 = b, a4 = 23
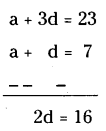 d = 16/2
d = 16/2
d = 8
a + 8 = 7.
a = 7 - 8
a = -1
b = a3 = a + 2d = -1 + 2(8)
= -1 + 16
= 15
b = 15 ∴ a = -1, b = 15
Question 9.
Show that (a - b)2, (a2 + b2) and (a + b)2 are in A.P.
Solution:
Given (a - b)2, (a2 + b2) and (a + b)2 are in A.P.
a2 - a1 = a2 + b2 - (a - b)2
= a2 + b2 - (a2 - 2ab + b2)
= a2 + b2 - a2 + 2ab - b2 = 2ab
a2 - a2 = (a + b)2 - (a2 + b2)
= a2 + 2ab + b2 - a2 - b2 = 2ab
Common difference is same
d = 2ab
∴ (a - b)2, (a2 + b2) and (a + b)2 are in AP.
Question 10.
In an A.P. if the sum of third and seventh term is zero, find its 5th term.
Solution:
Given in AP
a3 + a7 = 0
a + 2d + a + 6d = 0
2a + 8d = 0
2(a + 4d) = 0
a + 4d = 0/2 = 0
a + 4d = 0
a5 = 0
∴ 5th terms is ‘0’.
Question 11.
Write the next two terms of the A.P.
√27, √48,√75, ...
Solution:
Given AP, √27, √48,√75, ...
√9×3, √16×3, √25×3, ....
= 3√3, 4√3, 5√3
a = 3√3
d = 4√3 - 3√3 = √3
a4 = a + 3d
= 3√3 + 3(√3) = 6√3
= √6×6×3 = 108
a5 = a + 4d
= √3 + 4√3 = 5√3 = √5×5×3 = √125
Question 12.
Which term of the A.P. 3,8,13,18,.. is 78 ?
Solution:
Given AP 3, 8, 13, 18, ..., 78.
a = 3, d = 8 - 3 = 5
an = 78
a + (n - 1) d = 78
3 + (n - 1) 5 = 78
(n - 1) 5 = 75
n - 1 = 15
n = 15 + 1
n = 16
∴ 16th term of AP is 78.
Question 13.
For an AP with common difference 6, the sum of first ten terms is same as four times the sum of first five terms. Determine the first term of the AP.
Solution:
Given in an AP d = 6.
a1 + a2 + .... a10 - 4(a1 + a2 + ... a5)
a + a + d + a + 2d + a + 3d + a + 4d + a + 5d + a + 6d + a + 7d + a + 8d + a + 9d = 4(a + a + d + a + 2d + a + 3d + a + 4d)
10a + 45d = 4(5a + 10d)
10a + 45d = 20a + 40d
20a + 40d - 10a - 45d = 0
10a - 5d = 0
10a = 5d
2a = d
2a = 6 ⇒ a = 3
Question 14.
Find the common difference of the terms of A.P.
(x - y), (x + y), (x + 3y), ......
Solution:
Given terms of A.P = (x - y), (x + y), (x + 3y) then common difference = difference of successive terms
= (x + y) - (x - y) = x + y - x + y = 2y
∴ Common difference of given AP = 2y
Question 15.
Check whether - 25 is a term in the progression 5, 3, 1, .... or not ?
Solution:
The given 5, 3, 1, ... is an arithmetic progression here
a = 5, d = a2 - a1 = 3 - 5 = -2
Let - 25 is some of ‘n’,th term
i.e. an = -25
So an = a + (n - 1)d
- 25 = 5 + (n - 1)(- 2)
- 25 - 5 = (n - 1) (-2)
-30/-2 = n - 1
⇒ n - 1 = 15 and n = 15 + 1 = 16
So - 25 exist at 16th term in above series.
Question 16.
Show that the sum of multiples of 3 between 1 and 100 is 1683.
Solution:
To show the sum of multiples of 3 between 1 and 100 is 1683. .
The multiples of 3, in between 1 and 100 are 3, 6, 9, 12, .99 which is an A.P.
In which a = 3, d = 6 - 3 = 3
and number of terms = 99/3 =33.
Now sum of 33 terms of A.P. 3, 6, 9, .. 99 is
Sn = n/2(a + l) = 33/2 (3 + 99)
= 33×102/2 = 51 × 33
∴ Sum of multiples of ’31’ = 1683
Question 17.
Find the 8th term of the A.P.,
117, 104, 91, 78, ....
Solution:
In the given A.P., a1 = 117, a2 = 104
Common difference d = a2 - a1
= 104 - 117
= - 13
∴ 8th term t8 = a1 + 7d
= 117 + 7(-13)
= 117 - 91 = 26
Question 18.
Write the formula to find nth term of A.P. and explain the terms in it.
Solution:
nth term of AP
an : a + (n - 1) d
a : first term
d : common difference
Question 19.
The hand borewell driller charges Rs. 200 for the first one meter only and raises drilling charges @ 30/- for every subsequent meter. Write a progression for the above data.
Solution:
Cost of first meter = Rs. 200
For every subsequent meter = Rs. 30 raised.
So the progression = 200, 230, 260,.
Question 20.
Write the common difference of an Arithmetic Progression, whose nth term is given by tn = 3n + 7.
Solution:
Given nth term of an A.P. = tn = 3n + 7
First term of an A.P. = n = 1
⇒ t1 = 3 . 1 + 7 = 10
Second term of an A.P. = n = 2
⇒ t2 = 3 . 2 + 7 = 13
Third term of an A.P. = n = 3
⇒ t3 = 3 . 3 + 7 = 16
Common difference = d = t2 - t1
t3 - t2
= 13 - 10
= 16 - 13
= 3
Question 21.
Find the sum of first 200 natural numbers.
Solution:
Formula for the sum of first n natural numbers is Σn = n(n+1)/2 put n = 200 in above formula.
We get
Σ200 = 200×(200+1)/2
= 200×201/2 = 20,100
Question 22.
Is ‘zero’ a term of the Arithmetic Progression 31, 28, 25, .... ? Justify your answer.
Solution:
a = 31 ; d = 28 - 31 = -3
an = a + (n - 1)d
0 = 31 + (n - 1)(-3) ⇒ n = 34/3
∴ zero is not a term of the given arithmetic progression.
Since ‘n’ is number of the term, it should be a whole number.
Question 23.
Is the sequence √3, √6, √9, √12, .. form an Arithmetic Progression ? Give reason.
Solution:
Given sequence √3, √6, √9, √12, .....
a2 - a1 = √6 - √3 = √3 (√2 - 1)
a3 - a2 = √9 - √6 - √3 (√3 - √2)
a2 - a1 ≠ a3 - a2
so it is not an Arithmetic progression.
Question 24.
For the A.P.; - 3, - 7, - 11, ; can
we find directly a30 - a20 without actually finding a30 and a20.
Solution:
Given A.P. - 3, -7, -11, ..
a = - 3, d = -7 - (-3) = -4
a30 - a20 = (a + 29d) - (a + 19d)
= a + 29d - a - 19d
= 10d = 10(- 4)
= -40
Question 25.
Find the 10th term of the arithmetic progression 3, 5, 7, ..
Solution:
3, 5, 7, .... A.P
a = 3, d = 2, n = 10
an = a + (n - 1)d
a10 = 3 + (10 - 1)2
= 3 + (9 × 2) = 3 + 18 = 21
10th Class Maths Arithmetic Progressions 4 Marks Important Questions
Question 1.
In which of the following situations, the sequence of numbers formed will form an A.P?
0 The cost of digging a well for the first metre is Rs. 150 and rises by Rs. 20 for each succeeding metre.
Solution:
Given, the cost of digging for the first metre = ₹ 150
Additional charge for each succeeding metre = ₹ 20
Cost of digging for the two metres = ₹ 150 + ₹ 120 = ₹ 170
Cost of digging for the three metres = ₹ 150 + ₹ 20 + ₹ 20 = ₹ 190
150, 170, 190, .... forms an A.P as each succeeding term is obtained by adding 20 its preceding term.
ii) The amount of air present in the cylinder when a vacuum pump removes each time 1/4 of their remaining in the cylinder.
Solution:
Let amount of air in the cylinder = x units
Amount of air removes first time = 1/4 x.
So, air in the cylinder after first time = 3/4 x
Amount of air removes second time = 1/4 of 3/4 x = 3/16 x
So, x, 3/4 x, ... is not in the form of A.P. Because, each succeding term is not obtained by subtracting of its preceding term.
Question 2.
Which term of the A.P 5, 15, 25, .. will be 130 more than its 31st term ?
Solution:
Given A.P is 5, 15, 25, ...
a = 5, d = a2 - a1 = 15 - 5 = 10, n = 31
We know that, an = a + (n - 1) d
a31 = 5 + (31 - 1) 10
= 5 + 30 x 10
a31 = 305
Let an = 130 + a31
an = a + (n - 1) d = 130 + 305
⇒ 5 + (n - 1) 10 = 435
(n - 1) = 435-5/10 = 430/10
n = 43 + 1
∴ n = 44
Therefore, 44th term of given A.P is 130 more than its 31st term.
Question 3.
Find the term of the A.P : 9, 12, 15, 18, . which is 39 more than its 36th term ?
Solution:
Given A.P is 9,12, 15, 18,.
a = 9, d = a2 - a1 = 12 - 9 = 3
We know that,
an = a + (n - 1) d
a36 = 9 + (36 - 1) 3
= 9 + 35 × 3
a36 = 9 + 105 = 114
an = a + (n - 1) d = a36 + 39
⇒ 9 + (n - 1) 3 = 114 + 39
⇒ (n - 1)3 = 153 - 9 = 144
⇒ (n - 1) = 144/3 = 48
∴ n = 48 + 1 = 49
Therefore 49th term is 39 more than its 36th term.
Question 4.
The 24th term of an A.P is twice its 10th term. Show that its 72nd term is 4 times its 15th term.
Solution:
We know that an = a + (n - 1) d in A.P.
a24 = a + 23d
a10 = a + 9d
Given, a24 = 2.a10
a + 23d = 2 (a + 9d)
a + 23d = 2a + 18d
a - 2a = 18d - 23d
- a = -5d
a/d = 5/1
⇒ a = 5, d = 1
a15 = a + 14d = 5 + 14 (1) = 19
a72 = a + 71d = 5 + 71 (1)
a72 = 76 = 4 × 19 = 4 . a15
Therefore, a72 = 4 . a15
Question 5.
In an A.P the first term is 8, nth term is 33 and the sum of first n terms is 123, fold n and d.
Solution:
Given, first term a = 8, an = 33
We know that
an = a + (n - 1) d in A.P.
⇒ 8 + (n - 1) d = 33
⇒ (n - 1) d = 33 - 8 = 25
⇒ (n - 1) d = 25 → (1)
Sum of ’n’ terms
Sn = n/2 [2a + (n - 1) d] = 123
⇒ n/2 [2 × 8 + (n - 1) d] = 123 → (2)
Put (1) in (2)
n/2 [16 + 25] = 123
⇒ n (41) = 123 × 2
n = 123×2/41 = 6
∴ n = 6
Put n = 6 in (1)
⇒ (6 - 1) d = 25
⇒ d = 25/5 = 5
∴ Therefore, n = 6 and d = 5
Question 6.
Find the common difference of the A.P and write the next two terms of 51, 59, 67, 75, .
Solution:
Given A.P : 51, 59, 67, 75,.
first term a = 51,
common difference d = a2 - a1
= 59 - 51 = 8
a5 = a + 4d = 51 + 4(8) = 51 + 32 = 83
a6 = a + 5d = 51 + 5(8) = 51 + 40 = 91
next two terms in A.P are : 83, 91.
Question 7.
Show that the sequence is given by an = 5n - 7 in an A.P, find its common difference.
Solution:
Given an = 5n - 7
If n = 1 then a1 = 5(1) - 7 = 5 - 7 = -2
If n = 2 then a2 = 5(2) - 7 = 10 - 7 = 3
If n = 3 then a3 = 5(3) - 7 = 15 - 7 = 8
If n = 4 then a4 = 5(4) - 7 = 20 - 7 = 13
Sequence is -2, 3, 8, 13,.
common difference
d = a2 - a1 = 3 - (-2) = 3 + 2 = 5
a3 - a2 = 8 - 5 = 5
= a4 - a3 = 13 - 8
Common difference is same.
So, given sequence an = 5n - 7 is in A.P.
Question 8.
Find the 12th, 20th and nth term of the A.P given by 9, 13, 17, 21, 25,.
Solution:
Given A.P : 9, 13, 17, 21, 25, .
first term a = 9,
common difference d = 13 - 9 = 4
nth term in A.P an = a + (n - 1) d
an = 9 + (n - 1)4 = 9 + 4n - 4 = 4n + 5
12th term a12 = 4(12) + 5 = 48 + 5 = 53
20th term a20 = 4(20) + 5 = 80 + 5 = 85.
Question 9.
Which term of the A.P 3, 8, 13, . is 248 ?
Solution:
Given A.P : 3, 8, 13, .
first term a = 3,
common difference d = a2 - a1
= 8 - 3 = 5
nth term in A.P an = a + (n - 1) d ,
⇒ 3 + (n - 1) 5 = 248
⇒ (n - 1) 5 = 248 - 3
⇒ (n - 1) 5 = 245
n - 1 = 245/5 = 49
n = 49 + 1 = 50
Therefore, 50th term is 248.
Question 10.
How many terms are there in A.P - 1, - 5/6, - 2/3, - 1/2, ..., 10/3
Solution:
Given A.P : -1, - 5/6, - 2/3, - 1/2, ..., 10/3 first term a = -1,
common difference = a2 - a1
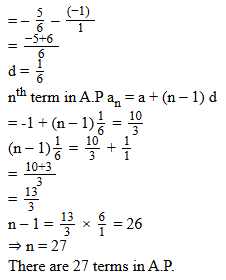
Question 11.
Find the sum of (-5) + (-8) + (-11) + . + (-230).
Solution:
Given (-5) + (-8) + (-11) + . + (-230)
First term a = -5,
Common difference d = a2 - a1
last term l = -230 = -8 - (-5)
= -8 + 5 = -3
nth term an = an + (n - 1) d
⇒ -5 + (n - 1) (-3) = -230
⇒ -5 - 3n + 3 = -230
⇒ -2 - 3n = - 230
⇒ -3n = -230 + 2 = -228
n = -228/-3 = 76
n = 76
Sum of n terms in A.P
Sn = n/2 (a + l)
= 76/2 [-5 + (-230)
= 38 (-235)
Therefore, sum of n terms Sn = - 8930
Question 12.
The sum of first 15 terms of an A.P. is 750 and its first term is 15. Find its 20th term.
Solution:
In an AP a =15
S15 = 750
n/2 (2a + (n - 1) d) = 750
15/2 (2 × 15 + (15 - 1) d) = 750
30 + 14d = 750 × 15/2
30 + 14d = 100
14d = 70
d = 5
a20 = a + 19d
= 15 + 19(5)
= 15 + 95
= 110.
Question 13.
Rohan repays hit total loan of ₹ 1,18,000 by paying every month, starting with the first instalment of ₹ 1,000. If he increases the instalment by ₹ 100 every month, what amount will be paid by him in the 30th instalment? What amount of loan he paid after 30th instalment ?
Solution:
From the given information, the A.P so formed is
1000, 1100, 1200, ....
a = 1000, d = 1100 - 1000= 100
a30 = a + 29d
= 1000 + 29(100)
= 1000 + 2900 = 3900
Amount paid in 30th instalment is 3900.
Loan paid after 30th instalment.
= 118000 - S30
= 118000 - 30/2 (2 × 1000 + (30 - 1) 100)
= 118000 - 15 (2000 + 2900)
= 118000- 15 (4900)
= 118000 - 73500 = ₹ 44500
Question 14.
Show that the sum of all terms of an A.P. whose first term is a, the second term is b and the last term is c is equal to (a+c)(b+c-2a)/2(b-a).
Solution:
In AP, first term = a.
second term = b.
last term = c.
d = b - a
an = a + (n - 1) d
c = a + (n - 1) (b - a)
c - a = (n - 1) (b - a)
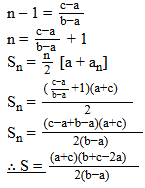
Question 15.
Solve the equation :
1 + 4 + 7 + 10 + .... + x = 287.
Solution:
Given AP 1 + 4 + 7 + 10 ... + x = 287.
a = 1
d = 4 - 1 = 3
Sn = 287
n/2 (2a + (n - 1)d) = 287
287 = n/2 (2 × 1 + (n - 1) 3)
574 = n(2 + 3n - 3)
574 = n(3n - 1)
3n2 - n - 574 = 0
3n2 - 42n + 41n - 574 = 0
3n (n - 14) + 41 (n - 14) = 0
(n - 14) (3n + 41) = 0
n - 14 = 0 (or) 3n = -41
n = 14 (or) n = -14/3
but n = 14 only
a + (n - 1) d = x
1 + (14 - 1) 3 = x
1 + 13(3) = x
1 + 39 = x
x = 40
Question 16.
Find the number of terms in the following
AP. 7, 13, 19, ..., 205.
Solution:
Given: 7, 13 19 ...., 205 are in A.P
a = 7, d = 6
Let an = 205
a + (n - 1)d = 205
7 + (n - 1)6 = 205
(n - 1)6 = 205 - 7
(n - 1)6 = 198
(n - 1) = 33
∴ n = 34
Number of terms in the given AP. is 34.
Question 17.
nth term of an A.P. is an. If a1 + a2 + a3 = 102 and a1 = 15, then find a10.
Solution:
Given a1 = 15 and a1 + a2 + a3 = 102
a + a + d + a + 2d = 102
⇒ 3a + 3d = 102
⇒ 3(a + d) = 102
∴ (a + d) = 102/3 = 34
⇒ d = 34 - a = 34 - 15 = 19
∴ a = 15, d = 19
then its 10th term = a10
= a + (10 - 1)d
= a + 9d
= 15 + 9(19)
= 15 + 171
= 186
∴ 10th term of it = 186
Question 18.
How many three digit numbers are divisible by 3 ?
Solution:
3 Digit numbers which are divisible by
3 are 102, 105, 108, .... 999
a = 102, d = 3, nth term = 999
a + (n - 1)d = 999
102 + (n - 1).3 = 999
⇒ (n - 1)3 = 897
n - 1 = 897/2 = 299
⇒ n = 300
∴ No. of three digit numbers which are divisible by 3 is 300.
Question 19.
If the sum of first 15 terms of an A.P. is 675 and its first term is 10, then find 25th term.
Solution:
In an A.P. first term = a = 10
Sum of first 15 terms
= S15 = 15/2 (2a + 14d) = 675
⇒ 15/ × 2(10 + 7d) = 675
⇒ 10 + 7d = 675/15
⇒ 10 + 7d = 45
⇒ 7d = 35
∴ d = 5
∴ 25th term = a25
= a + 24d
= 10 + 24 × 5
= 10 + 120
= 130
Question 20.
In a flower garden there are 23 plants in first row, 21 plants in second row, 19 plants in 3rd row and so on. If there are 10 rows in that garden, then find the total number of plants in the last row with the help of the formula tn = a + (n - 1)d.
Solution:
No. of plants in 1st row = 23
No. of plants in 2nd row = 21
No. of plants in 3rd row =19 and so on.
So the progression is 23, 21, 19, .....
in this AP. a = 23, d = 21 - 23 = -2
n = 10
tn = a + (n - 1) d
t10 = 23 + (10 - 1) (-2)
= 23 + 9(-2) = 23 - 18 = 5
Number of plants in the last row = 5.
Question 21.
If seven times of 7th term of an Arithmetic Progression is equal to the 11 times of 11th term of it, then find the 18th term of that Arithmetic Progression.
Solution:
In an A.P. 7th term be a + 6d and 11th term be a + 10 d
Seven times of 7th term is equal to 11 times of 11th term.
7(a + 6d) = 11(a + 10d)
7a + 42d = 11a + 110d
⇒ 11a -7a + 110d - 42d = 0
⇒ 4a + 68d = 0
⇒ 4(a + 17d) = 0
⇒ a + 17d = 0/4 = 0
a + (18 - 1)d = 0 {? tn = a + (n - 1)d}
18th term of an A.P. is zero.
Question 22.
Explain the terms in the formula
S
n = n/2 [2a + (n - 1)d].
Solution:
Sn = n/2 [2a + (n - 1)d]
Sn = sum of ‘n’ terms of an A.P.
a = first term of A.P.
d = common difference of A.P.
n = number of terms.
Question 23.
Find the sum of first 10 terms of an A.P.
3, 15, 27, 39, ....
Solution:
a = 3 ; d = 15 - 3 = 12 ; n = 10
Sn = n/2 [2a + (n - 1)d]
S10 = 10/2 [2(3) + (10 - 1)12]
= 5 [6 + 108]
= 5 × 114 = 570
Question 24.
Find the 7th term from the end of the Arithmetic Progression
7, 10, 13, ..., 184.
Solution:
Given Arithmetic progression
7, 10, 13, ..., 184.
Writing it in the reverse
184, 181, .., 13, 10, 7
a = 184 ; d = 181 - 184 = -3.
an = a + (n - 1)d
7th term son = 7
a7 = 184 + (7 - 1) (-3)
- 184 - 6(3) = 184 - 18 = 166.
Question 25.
Which term of the AP. 21, 18, 15, .... is - 81 ? Also find the term which becomes zero.
Solution:
Arithmetic progression 21, 18, 15, ..
a = 21, d = 18 - 21 = -3 ; an = -81
n = ?
an = a + (n - 1)d
- 81 = 21 + (n - 1)(- 3)
(n - 1)(- 3) = - 81 - 21 = -102
n - 1 = -102/-3 = 34
n = 34 + 1 = 35
∴ -81 is 35th term of thai A.P
again an = 0 ; n
an = a + (n - 1)d
0 = 21 +(n - 1)(-3)
(n - 1)(-3) = -21
n - 1 = -21/-3 = 7
n - 1 = 7 ⇒ n = 7 + 1 = 8
∴ 8th term of that A.P is zero.
Question 26.
In an arithmetic progression, if 4 times of fourth term is equal to 8 times of the eighth term, then prove that twelfth term of the progression is zero.
Give that
In an AP it 4 times of fourth term is equal to 8 times of the eighth term.
4(4
th term) = 8(8
th term)
4(a + 3d) = 8 (a + 7d)
4a + 12d = 8a + 56d
8a - 4a + 56d - 12d = 0
4a = - 44 d ⇒ a = -44 d/4
a = -11d
So, 12
th term ⇒ a
12 = a + 11d
We know that a = -11d
So, a
12 = -11d + 11d
a
12 = 0
∴ Hence proved.
10th Class Maths Arithmetic Progressions 8 Marks Important Questions
Question 1.
The sum of 5th and 9th terms of an A.P is 72 and the sum of 7th and 12th terms is 97. Find the A.P.
Solution:
We know that, nth term in A.P is
an = a + (n - 1) d
a5 + a9 = 72
a + 4d + a + 8d = 72
2a + 12d = 72
2a = 72 - 12d → (1)
a7 + a12 = 97
⇒ a + 6d + a + 11d = 97
⇒ 2a + 17d = 97 → (2)
Put (1) in (2)
⇒ 72 - 12d + 17d = 97
⇒ 5d = 97 - 72
⇒ 5d = 25
∴ d = 25/5 = 5
Put d = 5 in (1)
2a = 72 - 12 × 5
2a = 72 - 60 = 12
∴ a = 12/2 = 6
?, a + d, a + 2d, a + 3d, .
6, 6 + 5, 6 + (2 × 5), 6 + (3 × 5), .
Therefore, A.P is 6, 11, 16, 21, .
Question 2.
The 10th and 18th terms of an A.P are 41 and 73 respectively. Find 26th term.
Solution:
Given a10 = 41, a18 = 73
We know that,
an = a + (n - 1) d
a10 = a + (10 - 1) d = 41
⇒ a + 9d = 41 → (1)
a18 = a + 17d = 73 → (2)
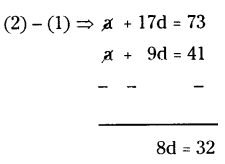 ∴ d = 32/8 = 4
∴ d = 32/8 = 4
Put d = 4 in (1) ⇒ a + 9 (4) = 41
⇒ a = 41 - 36 = 5
a26 = a + 25d
= 5 + 25(4)
= 5 + 100
a26 = 105
Therefore, 26th term is 105.
Question 3.
The 19th term of an A.P is equal to three times its sixth term. If its 9th term is 19, find the A.P.
Solution:
We know that an in A.P is
an = a + (n - 1) d
a19 = a + 18d, a6 = a + 5d
a19 = 3.a6
a + 18d = 3 (a + 5d)
a + 18d = 3a + 15d
a - 3a = 15 d - 18d
-2a = -3d ⇒ a = 3d/2 → (1)
Given a9 = a + 8d = 19 → (2)
Put (1) in (2) ⇒ 3d/2 + 8d/2 = 19
⇒ 3d+16d/2 = 19
⇒ 19d/2 = 19
d = 19 2/19
∴ d = 2
Put d = 2 in (1) ⇒ a = 3(2)/2 = 3
a, a + d, a + 2d, .
3, 3 + 2, 3 * 2 (2), .
Therefore, A.P is 3, 5, 7, .
Question 4.
In an A.P the sum of first ten terms is -150 and the sum of its next ten terms is -550. Find the A.P.
Solution:
We know that
Sn = n/2 [2a + (n - 1) d] in A.P.
S10 = 10/2 [2a + (n - 1) d] = -150
⇒ 2a + 9d = -150/5 = -30
⇒ 2a + 9d = -30 → (1)
S20 = Sum of 10 terms + Sum of 11th term to 20th terms
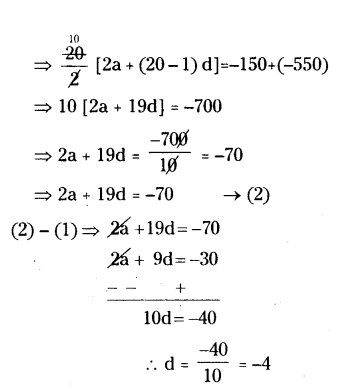 Put d = -4 in (1)
Put d = -4 in (1)
⇒ 2a + 9 (-4) = -30
⇒ 2a = - 30 + 36 = 6
∴ a = 6/2 = 3
a, a + d, a + 2d, .
3, 3 + (-4), 3 + 2 (-4), .
Therefore, A.P is 3, -1, -5, .
Question 5.
Sum of the first 14 terms of an A.P is 1505 and its first term is 10. Find its 25th term.
Solution:
Given, first term a = 10
We know that,
Sn = n/2 [2a + (n - 1)d] in A.P.
S14 = 14/2 [2 × 10 + (14 - 1) d] = 1505
⇒ 20 + 13d = 1505/7
⇒ 13d = 215 - 20
⇒ 13d = 195
⇒ d = 195/13
Therefore, d = 15
S25 = 25/2 [2 × 10 + (25 - 1)15]
= 25/2 [20 + 24 × 15]
S25 = 25/2 × 380 = 4750
Therefore 25th term is 4750.
Question 6.
The nth term of an A.P is given by (- 4n + 15). Find the sum of first 20 terms of this A.P.
Solution:
Given, an = -4n +15
a1 = - 4 (1) + 15 = - 4 + 15 = 11
a2 = -4(2) + 15 = - 8 + 15 = 7
a3 =-4(3) + 15 = - 12 + 15 = 3
A.P is 11, 7, 3, .
a = 11, d = a2 - a1 = 7 - 1 = -4
We know that,
Sn = n/2 [2a + (n - 1) d]
S20 = 20/2 [2 × 11 + (20 - 1) (-4)]
= 10 [22 - 19 × 4]
= 10 (22 - 76) = 10 × -54
S20 = -540
Therefore, sum of first 20 terms in A.P is -540.
Question 7.
Find the number of terms of the A.P : -12, -9, -6, . . . 21. If 1 is added to each term of this A.P, then find the sum of all terms of the A.P thus obtained.
Solution:
Given A.P is -12, -9, -6, . , 21.
a = -12, d = -9 - (-12) = - 9 + 12 = 3
We know that,
an = a + (n - 1) d
⇒ -12 + (n - 1) 3 = -21
⇒ (n - 1) 3 = 21 + 12 = 33
⇒ n - 1 = 33/3 = 11
∴ n = 11 + 1 = 12
In the given A.P. number of terms are 12.
If 1 is added to given A.P.
then, -12 + 1, -9 + 1, -6 + 1, . , 21 + 1
New A.P is-11,-8,-5,., 22
a = -11, d = a2 - a1 = -8 - (-11) = -8 + 11 = 3
Last term l = 22,
Sum of 12 terms is S12 = n/2 (a + 1)
= 12/2 [-11 + 22]
S12 = 6 × 11 = 66
Therefore, sum of all terms obtained is 66.
Question 8.
If pth term of A.P is q and the qth is p. Prove that its nth term is (p + q - n).
Solution:
Let first term a and common difference d in A.P an = a + (n - 1) d
We know, nth term
then pth term ap = a + (p - 1) d = q → (1)
qth term aq = a + (q - 1) d = p → (2)
By subtract (2) from (1)
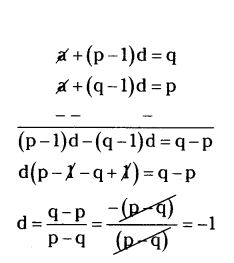 put d = -1 in (1)
put d = -1 in (1)
a + (p - 1) (-1) = q
a - (p - 1) = q
a = q + p - 1
Now, nth term = (q + p - 1) + (n - 1) (-1)
= q + p - 1 - n + 1
Therefore nth term = p + q - n
Question 9.
If 9th term of an A.P is equal to 6 times its second term and its 5th term is 22 find the A.P.
Solution:
We know,
nth term in A.P an = a + (n - 1) d
If n = 2 then a2 = a + (2 - 1) d = a + d
If n = 9 then a9 = a + 8d
If n = 5 then a5 = a + 4d = 22 → (1)
a9 = 6.a2
a + 8d = 6(a + d)
a + 8d = 6a + 6d
8d - 6d = 6a - a
2d = 5a
d = 5a/2
Put d = 5a/2 in (1)
a + 4(5a/2) = 22
a + 10a = 22
11a = 22
a = 22/11 = 2
Put a = 2 in (1)
2 + 4d = 22
4d = 22 - 2 = 20
d = 20/4 = 5
A.P is : a, a + d, a + 2d, a + 3d, ..
2, 2 + 5, 2 + (2 × 5), 2 + (3 × 5), ..
∴ A.P = 2, 7, 12, 17, ..
Question 10.
A manufacturer of TV sets produced 500 sets in the third year and 700 sets in the seventh year. Assuming that the production increase uniformly by a fixed number every year. Find
i) the production of TV sets in the 15 th year.
ii) the total production of TV sets in the first ten years.
Solution:
Since the production increases uniformly by a fixed number every year, the number of TV sets manufactured in 1st, 2nd, 3rd, years will form an A.P.
Let us denote the number of TV sets manufactured in the nth year by an.
Then, a3 = 500 and a7 = 700
a + 2d = 500 and a + 6d = 700
By solving these equations
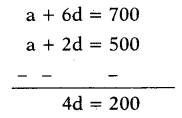 ⇒ d = 200/4 = 50
⇒ d = 200/4 = 50
a + 2d = 500
⇒ a + 2 × 50 = 500
⇒ a = 400
i) Now, a15 = a + 14d
= 400 + 14 × 50
= 400 + 700
= 1100
So, production of TV sets in the 15th year is 1100.
ii) Also, S10 = 10/2 [2 × 400 + (10 - 1)50]
= 5[800 + 450]
= 5[1250]
= 5 × 1250
= 6250
Question 11.
Find the sum of all 3 digit numbers that are divisible by 4.
Solution:
The 3 digit numbers are 100, 101, 102 .... 999 among them the number divisible by 4 are 100, 104, 108, ... 996 which is an A.P the first term a = 100
Common difference = a2 - a1
= 104 - 100 = 4
Let the number of terms = n
The nth term an = 996
an = a + (n - 1)d
996 = 100 + (n - 1) 4
996-100/4 = n - 1
896/4 = n - 1 = 224
⇒ n = 224 + 1 = 225
Now formula for sum of ‘n’ terms in AP is
Sn = n/2 [a + l] = 225/2 [100 + 996]
= 225×1096/2 = 1,23,300
Question 12.
Find the sum of all the integers between 1 to 50 which are not divisible by 3.
Solution:
[1, 4, 7, 10, .... 49] + [2, 5, 8, .... 50]
Case (i): [1,4, 7, 10, ..... 49]
Here a = 1, d = 3
an = a + (n- 1) d
49 = 1 + (n - 1) 3 ⇒ 49 = 3n - 2
49 + 2 = 51 = 3n
n = 51/3 = 17
Sn(1) = n/2 [2a + (n - 1) d]
= 17/2 [2(1) + (17 - 1) 3]
= 17/2 × 50 = 425
Case (ii): [2, 5, 8, .... 50]
a = 2, d = 3
an = a + (n- 1) d .
50 = 2 + (n - 1) 3 = 3n - 1 ⇒ 51/3 = n
∴ n = 17
Sn(2) = 17/2 [2(2) + (17 - 1) 3]
= 17/2 [4 + 48] = = 17/2 [52] = 442
Adding case (i) & case (ii)
Sn = 425 + 442 = 867.
Question 13.
A sum of Rs. 1,000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests for 1st, 2nd and 3rd years form an A.P. ? If so, find the total interest to be paid for 30 years making the use of this fact.
Solution:
Sum invested = P = Rs. 1000
Rate of interest = R = 8%
Time of investment = 1 year ,
∴ Amount of interest (simple)
I = PTR/100 = 1000×1×8/100 = Rs. 80
Amount of interest for 2 years
PTR/100 = 1000×2×8/100 = Rs. 160
Amount of interest for 3 years
PTR/100 = 1000×3×8/100 = Rs. 240
So the amount of interest for the years 1, 2, 3, ... are
80, 160, 240, ... are in an A.P.
In which the first term (a) = 80
Common difference (d) = a2 - a1
= 160 - 80 = 80
∴ The amount of interest to be paid in 30 years of time = S30
Sn = n/2 [2a + (n - 1)d]
= 30/2 [2(80) + (30 - 1) 80]
= 15[ 160 + 29(80)]
= 15[ 160 + 2320]
= 2480 × 15
= Rs. 37200
∴ Rs. 37200 will be paid towards interest for 30 years.
Question 14.
If the sum of first 7 terms and 15 terms of an A.P. are 98 and 390 respectively, then find thd sum of first 10 terms.
Solution:
Sum of the first 7 terms of AP = 98
7/2 [2a + (7 - 1)d] = 98
2a + 6d = 98 × 7/2
2a + 6d = 28
a + 3d = 14 ______ (1)
Sum of the first 15 terms of AP = 390
15/2 [2a + (15 - 1)d] = 390
2a + 14d = 390 × 15/2
2a + 14d = 52
a + 7d = 26 _____ (2)
by solving (1) and (2)
a = 5 and d = 3
Sum of the first 10 terms
= 10/2 [2a + (10 - 1)d]
= 5[2(5) + 9(3)]
= 5[10 + 27]
= 5 × 37 = 185
Question 15.
A man saved ₹ 16,500 in- ten years. In each year, after the first, he saved ₹ 100 more than he did in the preceding year. How much did he save in the first year?
Solution:
Given that S10 = ₹ 16,500; d = ₹ 100; n = 10; a = ?
Sn = n/2 [2a + (n - 1)d]
16,500 = 10/2 [2a + (10 - 1) 100]
16,500 = 5(2a + 900)
16,500/5 = 2a + 900
3300 = 2a + 900
2a + 900 = 3300
2a = 2400
a = 2400/2 = 1200
He saved in the first year = ₹ 1200
Question 16.
An A.P. has 21 terms. The sum of 10th, 11th, 12th terms is 129. The sum of the last 3 terms is 237, then find the A.P.
Solution:
(a + 9d) + (a + 10d) + (a + 11d) - 129
3a + 30d = 129
a + 10d = 43 ... (1)
(a + 18d) + (a + 19d) + (a + 20d) = 237
3a + 57d = 237
a + 19d = 79 ... (2)
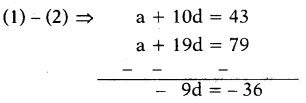 ∴ d = 4
∴ d = 4
‘d’ value substituting in equation (1)
a + 10(4) = 43
a = 43 - 40 = 3
∴ a = 3
∴ Required A.P, is 3, 7, 11, 15, 19, ....
AP 10th Class Maths 5th Lesson Important Questions and Answers Arithmetic Progressions
Question 1.
Check whether - 25 is a term in the progression 5, 3, 1, .....or not ?
Solution:
The given 5, 3, 1,......is an arithmetic
progression here
a = 5, d = a2 - a2 = 3 - 5 = -2
Let -25 is some of ‘n’th term
i.e. an - 25
So an = a + (n-1)d
-25 = 5 + (n - 1)(- 2)
- 25 - 5 = (n - 1) (-2)
-30/-2 = n - 1
⇒ n - 1 = 15 and n = 15+ 1 = 16
So - 25 exist at 16th term in above series.
Question 2.
Find out the common ratio in the GP 2, 2 √2, 4......
Solution:
The given GP is 2, 2√2, 4, ......
The common ratio = a2/a1=2√2/2
Question 3.
Show that the sum of multiples of 3 bet-ween 1 and 100 is 1683.
Solution:
To show the sum of multiples of 3 bet-ween 1 and 100 is 1683.
The multiples of 3, in between 1 and 100 are 3, 6, 9, 12,. 99 which is an A.P.
In which a = 3, d = 6 - 3 = 3
and number of terms = 99/3 = 33.
Now sum of 33 terms of A.P.
3, 6, 9, .. 99 is
Sn = n/2 (a + l)
= 33/2 (3 + 99)
= 33×102/2
= 51 × 33
∴ Sum of multiples of ‘3’ = 1683
Question 4.
Find the 8th term of the A.P., 117, 104, 91, 78, ......
Solution:
In the given A.P., a1 = 117, a2 = 104
Common difference d = a2 - a1
= 104 - 117
= -13
∴ 8th term t8 = a1 + 7d
= 117 + 7(-13)
= 117 - 91 = 26
Question 5.
Find the common difference of the terms of A.P.
(x - y), (x + y), (x + 3y), .....
Solution:
Given terms of A.P = (x - y), (x + y), (x + 3y)
then common difference = difference of successive terms
= (x + y) - (x - y) = x + y - x + y = 2y
∴ Common difference of given AP = 2y
Question 6.
1/4,1/16,1/64,1/256, ...... are in G.P. justify.
Solution:
To justify 1/4,1/16,1/64,1/256, ...... is a G.P.
We need to show the ratio of any two successive terms is equal.
Now the common ratio
= r1 1/16 ÷ 1/4 = 1/4
r2 = 1/64 ÷ 1/16 = 1/4 ⇒ r1 = r2
Hence it is a G.P.
Question 7.
State Fundamental Theorem of Arith-metic. Model PapeF
Solution:
Statement of Fundamental Theorem of Arithmetic "Every composite number can be expressed as a product of , primes, and this factorization is unique".
Question 8.
Find the numbe of terms in the follow¬ing A.P.
7,13,19, ....... ,205
Solution:
Given : 7, 13, 19 ......., 205 are in A.P
a = 7, d = 6
Let an = 205
a + (n - 1)d = 205 7 + (n - 1)6 = 205 .
(n- 1)6 = 205 -7 (n-1)6 =198 (n - 1) = 33 ⇒ n = 34
Number of terms in the given A.P is 34.
Question 9.
nth term of an A.P. is an . If a1 + a2 + a3 = 102 and a1 = 15, then find a10.
Solution:
Given a1 = 15 and a1 + a2 + a3 =102
a + a + d + a + 2d = 102
⇒ 3a + 3d = 102
⇒ 3 (a + d) = 102
∴ (a + d) = 102/3 = 34
⇒ d = 34 - a = 34 - 15 = 19
∴ a = 15, 0 = 19
then its 10th term = a10
= a + (10 - 1)d
= a + 9d = 15 + 9(19)
= 15 + 171 = 186
∴ 10th term of it = 186
Question 10.
How many three digit numbers are divisible by 3 ? Mar. *18|
Solution:
3 Digit numbers which are divisible by
3 are 102, 105, 108, ...... 999
a = 102, d = 3, nth term = 999
a + (n - 1)d = 999
102 + (n- 1) .3 = 999
(n- 1)3 = 897
n - 1 = 897/3 = 299
n = 300
∴ No. of three digit numbers which are divisible by 3 is 300.
Question 11.
If the sum of first 15 terms of an A.P. is 675 and its first term is 10, then find
25
th term.
Solution:
In an A,P. first term = a = 10
Sum of first 15 terms
S15 = 15/2 (2a + 14d) = 675
⇒ 15/2 x 2(10 + 7d) = 675
⇒ 10 + 7d = 675/15
⇒ 10 + 7d = 45
⇒ 7d = 35
∴ d = 5
∴ 25th term = a25 = a + 24d
= 10 + 24 × 5 = 10 + 120 = 130
Question 12.
The first term of a G.P. is 50 and 4th term is 1350. Find the 5th term.
Solution:
Let first term of a GP is ‘a’ and com¬mon ratio is ‘r’.
Given that t1 = a = 50
4th term t4 = ar3 = 1350
⇒ 50r3 = 1350 r3 = 1350/50 = 27
∴ r = 3
5th term t5 = ar4
Question 13.
Check whether -256 is term of G.P -4, -8, -16, .....
Solution:
The given GP = -4, -8, -16, .....
∴ a = -4, r = -8/-4 = 2
Let the given -256 is ‘n’th term of given GP.
∴ tn arn-1 = -256
⇒ -4(2)n-1 = -256
⇒ 2n-1 = -256/-4 = 64
2n-1 = 64 = 26
⇒ n -1 = 6
⇒ n = 6 + 1 = 7
-256 is ‘7’th term of given G.P.
Question 14.
A sum of Rs. 1,000 is invested at 8% simple interest per year. Calculate the interest at the end of each year. Do these interests for 1st, 2nd and 3 rd years form an A.P. ? If so, find the total in¬terest to be paid for 30 years making the use of this fact.
Solution:
Sum invested = P = Rs. 1000
Rate of interest = R = 8%
Time of investment = 1 year
∴ Amount of interest (simple)
 So the amount of interest for the
So the amount of interest for the
years 1, 2, 3, ......are
80, 160, 240,... are in an A.P.
In which the first term (a) 5= 80 Common difference (d) = a2 - a1
= 160 - 80 = 80
∴ The amount of interest to be paid in 30 years of time = S30
Sn = j [2a + (n- l)d]
= n/2 [2(80) + (30 - 1) 80]
= 15[160 + 29(80)]
= 15[160 + 2320]
= 2480 × 15 - Rs. 37200
∴ Rs, 37200 will be paid towards interest for 30 years.
Question 15.
If the sum of first 7 terms and 15 terms of an A.P. are 98 and 390 respectively, then find the sum of first 10 terms.
Solution:
Sum of the first 7 terms of AP = 98
7/2 [2a + (7-1)d] = 98
2a + 6d = 98 × 2/7
2a + 6d = 28
a + 3d = 14 .......(1)
Sum of the first 15 terms of AP = 390
15/2 [2a + (15 - 1)d] = 390
2a + 14d = 390 × 2/15
2a + 14d - 52
a + 7d = 26 .....(2)
by solving (1) and (2)
a = 5 and d = 3
Sum of the first 10 terms 10
= 10/2 [2a + (10 - 1)d]
- 5[2(5) + 9(3)]
= 5[10 + 27]
= 5 × 37 = 185
Question 16.
Check whether - 321 is a term of the A.P.: 22,15, 8, 1, ......
Solution:
Given A.P is 22, 15, 8, 1, .......
Let an = - 321
a = 22, d = -7
an = a + (n - 1)d
-321 = 22 + (n - 1) (-7)
- 321 = 22 - 7n + 7
- 321 - 29 - - 7n
- 350 - - 7n
n = 350/7 = 50
∴ - 321 be a term of given A.P. i.e., 50.
Question 17.
A man saved ₹ 16,500 in ten years. In each year, after the first, he saved ₹ 100 more than he did in the preceding year. How much aid he save in the first year?
Solution:
Given that S10 = ₹ 16,500; d = ₹ 100; n = 10; a = ?
Sn = n/2 [2a + (n - 1)d]
16,500 = 10/2 [2a + (10-1) 100]
16,500 = 5(2a + 900)
16,500/5 = 2a + 900
2a + 900 = 3300
2a = 2400
a = 2400/2 = 1200
He saved in the first year = ₹ 1200
Question 18.
An A.P. has 21 terms. The sum of 10th, 11th, 12th terms is 129. The sum of the last 3 terms is 237, then find the A.P.
Solution:
(a + 9d) + (a + 10d) + (a + 11d) = 129
3a + 30d = 129
a + 10d = 43 ......(1)
(a + 18d) + (a + 19d) + (a + 20d) = 237
3a + 57d = 237
a + 19d = 79 ......(2)
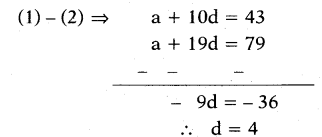 ‘d’ value substituting in equation (1)
‘d’ value substituting in equation (1)
a + 10(4) = 43
a = 43 - 40 = 3
∴ a = 3
∴ Required A.P. is 3, 7, 11, 15, 19,.
Question 19.
Find the 13th term of the A.P. 2, 7, 12, .......
Solution:
In the given A.P. 2, 7, 12, .......
The first term (a) = 2
Common difference (d) = a2 - a21
= 7 - 2 = 5
The required term (n) = 13
Formula for nth term in an A.P. is an = a + (n - 1) d ,
Then a13 = 2 + (13 -1)5 = 2 + 12 (5)
= 2 + 60 = 62
So 13th term = 62
Question 20.
In an A.P. the common difference (d) is 6 and seventh term is 36. Can we write such an A.P. ?
Solution:
Yes, we can write the above said A.P.
In the given A.P. (d) = 6
Seventh term a7 = 36
a7 = a + 6d = 36
⇒ a + 6 (6) = 36
∴ a = 36 - 36 = 0
∴ In the given progression a = 0 and d = 6 then it is 0, 6, 12, 18, ....
Question 21.
The ‘n’ th term of a given A.P. is 6n+2. Then write the first four terms in it.
Solution:
In the given A.P. an = 6n + 2
Then the first term = a1
= 6(1) + 2 = 6 + 2 = 8
Second term = a2 = 6 (2) + 2
= 12 + 2 = 14
Third term = a3 = 6 (3) + 2
= 18 + 2 = 20
Fourth term = a4 = 6 (4) + 2
= 24 + 2 = 26
So the first four terms in that A.P. are 8, 14, 20, 26.
Question 22.
In an A.P. the seventh term is 13 and 3rd term is 7. So find ‘a’ and ‘d’ in the method of elimination.
Solution:
In an A.P. the ‘n’th term = an
= a + (n - 1) d
Then a7 = a + (7 - 1) d
= a + 6d = 13 ......(1)
and a3 = a + (3 - 1) d
= a + 2d = 7 ...... (2)
Now solving equations (1) & (2) in elimination method
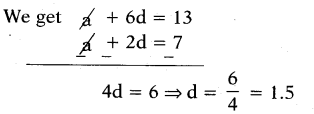 Then a + 2d = 7
Then a + 2d = 7
a + 2 (1.5) = 7 ⇒ a + 3 = 7
and a = 7 - 3 = 4
So a = 4 and d = 1.5
Question 23.
Which terms are to be known to cal-culate ‘n’ th term of A.P. ?
Solution:
The formula for ‘n’ th term of an A.P. is an = a + (n - 1) d
The variables in. the above formula are a, d, n .
So we should have the above three to calculate an.
Question 24.
Establish the relationship between the first and ‘n’th term of an A.P. in which ‘d’ = 0.
Solution:
Let the first term of that A.P. is ‘a’.
Then common difference (d) = 0 given then nth term = a + (n - 1) d
= a + (n - 1) (0)
= a + 0 = a
∴ an = a
So, when d = 0 is given the ‘n’th term of an A.P. (an) is equal to its first term (a).
Question 25.
What will be the salary of a person in the year 2020, whose salary in the year 2016 is Rs. 10,000, which in¬creases Rs. 1500 every year ?
Solution:
As the increase (increment) is fixed then it becomes an A.P.
His starting salary in 2016,
= First term of that AP (a)
So (a) = 10,000/-
Increase of salary in every year = Common difference
(d) = Rs. 1500/-
∴ His salary in 2020= 5th term in that A.P.
∴ a5 = a + (n - 1) d
= 10,000 + (5 - 1) (1500)
= 10,000 + 4 (1500)
= 10,000 + 6000 = 16,000/-
His salary in year 2020 is 16000/-
Question 26.
Parking fee for a two wheeler is Rs. 10 per day. i.e., for first day, and then after Rs. 2 for everyday. So what will be the amount to be paid for 15 days ?
Solution:
The additional payment for each day- is fixed. Hence the payments to be made are in G.P. .
Here in this problem
Charges for first day
= First term of AP (a)
∴ a = Rs. 10
Additional charge for each day = Rs. 2
∴ Common difference (d) = 2/-
∴ The A.P. is 10, 12, 14, 16, ....... (15 terms)
The total amount to be paid for 15 days is S15 = ?
Formula for Sn = [2a + (n - 1) d]
S15= n/2 [2(10) + (15-1) (2)]
S15= 15/2 [20 + 14(2)]
= 15/2 [20 + 28]
= 15/2 x 48
= 15 × 24 = 360.00
So he has to pay Rs. 360 for 15 days parking.