Pair of linear Equations in Two Variables

3rd Lesson Pair of Linear Equations in Two Variables Class 10 Important Questions with Solutions

10th Class Maths Pair of Linear Equations in Two Variables 1 Mark Important Questions

Question 1.
If the pair to linear equations x - y = 1, x + ky = 5 has a unique solution x = 2, y = 1, then find the value of k.

Solution:
x + ky = 5
x = 2, y = 1
⇒ 2 + k(1) = 5
⇒ k = 5 - 2
∴ k = 3

Question 2.
The pair of linear equations x + 2y + 5 = 0 and -3x - 6y + 1 = 0 has

A) a unique solution
B) exactly two solutions
C) infinitely many solutions
D) no solution

Solution:
D) Pair of linear eq’s are
x + 2y + 5 = 0 and
-3x - 6y + 1 = 0
a1/a2 = 1/-3 = -1/3
b1/b2 = 2/-6 = -1/3
c1/c2 = 5/1 = 5 a1/a2 = b1/b2 ≠ c1/c2
∴ The lines are parallel.
∴ No solution.

Question 3.
The pair of equations y = 0 and y = -7 has

A) one solution
B) two solutions
C) infinitely many solutions
D) no solution

Solution:
D) The two lines y = 0 and y = -7
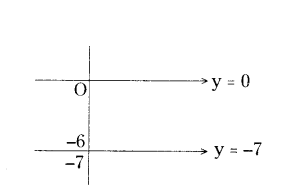∴ The two lines are parallel.
∴ No solution.

Question 4.
Graphically, the pair of equations given by 6x - 3y + 10 = 0, 2x - y + 9 = 0 represent two lines which are ........ .

A) intersecting at exactly one point
B) parallel
C) coincident
D) intersecting at exactly two points

Solution:
B) parallel
a1/a2 = b1/b2 ≠ c1/c2 ⇒ 6/2 = -3/-1 ≠ 10/9
The given lines are parallel.
∴ No solution.

Question 5.
What is the value of k for which the system of linear equations x + 2y = 3, 5x + ky + 7 = 0 is inconsistent ?

Solution:
Given, linear eq s are x + 2y = 3 and 5x + ky + 7 = 0
Inconsistent, a1/a2 = b1/b2 ≠ c1/c2
1/5 = 2/k
∴ k = 10

Question 6.
If a pair of linear equations are consistent, then the lines represented by them are ......

A) parallel
B) intersecting (or) coincident
C) always coincident
D) always intersecting

Solution:
B) intersecting (or) coincident

Question 7.
What are the values of x and y satisfying the two equations 32x + 33y = 34, 33x + 32y = 31 respectively ?

Solution:

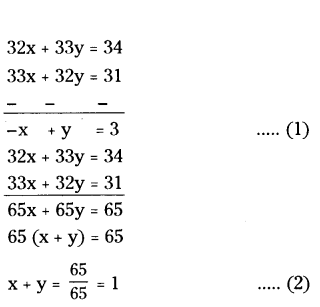
(1) + (2) ⇒ 2y = 4
⇒ y = 2
⇒ -x + 2 = 3
⇒ - x = 1
∴ x = -1, y = 2

Question 8.
Two lines are given to be parallel. The equation of one of the lines is 3x - 2y = 5. What can be the equation of the second line ?

Solution:
Given line is 3x - 2y = 5
To be parallel a1/a2 = b1/b2 ≠ c1/c2
⇒ 3/-12 = 1/-4, -2/8 = -1/4, c1/c2 = 5/7
∴ The required second equation is -12x + 8y + 7 = 0

Question 9.
What is the value of k for which the pair of linear equations x + y - 4 = 0, 2x + ky - 3 = 0 has no solution ?

Solution:
x + y - 4 = 0 and 2x + ky - 3 = 0
No solution, a1/a2 = b1/b2 ≠ c1/c2
⇒ 1/2 = 1/k
∴ k = 2

Question 10.
Perimeter of a rectangle whose length (l) is 4 cm more than twice, its breadth (b) is 14 cm. What is the pair of linear equation representing the above information ?

Solution:
breadth = b
length = 2b + 4
l = 2b + 4 ... (1)
P = 2(l + b)
14 = 2(l + b) ⇒ l + b = 7
⇒ l - 2b = 4 ... (2)

Question 11.
Find the solution of the pair of linear equation x = -5 and y = 6.

Solution:
(-5, 6)

Question 12.
What is the value of k for which the pair of linear equations 3x + 5y = 8 and kx + 15y = 24 has infinitely many solutions ?

Solution:
3x + 5y = 8
kx + 15y = 24
Infinitely many solutions
a1/a2 = b1/b2 = c1/c2
⇒ 3/k = 5/15
⇒ 3/k = 1/3
∴ k = 9

Question 13.
The point of intersection of the line represented by 3x - y = 3 and Y-axis is given by ....... .

Solution:
3x - y = 3
Let x = 0
⇒ 3(0) - y = 3
⇒ y = -3
Required point = (0, -3)

Question 14.
3 chairs and 1 table cost ₹ 900; where as 5 chairs and 3 tables cost ₹ 2,100. If the cost of 1 chair is ₹ x and the cost of 1 table is ₹ y. Then write the situation can be represented algebraically.

Solution:
3x + y = 900
5x + 3y = 2100

Question 15.
How many solutions has the pair of linear equations y = 0 and y = -5 ?

Solution:
The lines y = 0, y = -5 are parallel lines. No solution.

Question 16.
8 chairs and 5 tables cost ₹ 10,500, while 5 chairs and 3 tables cost ₹ 6450. What will be the cost of each chair will ?

Solution:
8x + 5y = 10500 .... (1)
5x + 3y = 6450 ..... (2)

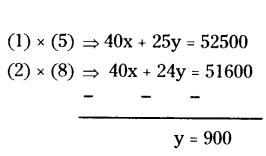
(2) ⇒ 5x + 2700 = 6450
∴ x = 750

Question 17.
If ABCD is a rectangle. Find the values of x and y.

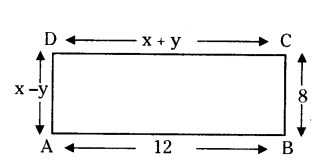
Solution:
x + y = 12
x - y = 8
2x = 20
x = 10
⇒ 10 + y = 12
⇒ y = 2

Question 18.
The pair of equations ax + 2y = 9 and 3x + by = 18 represent parallel lines, where a and b are integers, if

A) a = b
B) 3a = 2b
C) 2a = 3b
D) ab = 6

Solution:
D) ab = 6
ax + 2y = 9 and 3x + by = 18
parallel, a1/a2 = b1/b2 ≠ c1/c2
⇒ a/3 = 2/b
∴ ab = 6

Question 19.
The pair of linear equations
x + 2y - 5 = 0 and 2x - 4y + 6 = 0

A) is inconsistent
B) is consistent with many solutions
C) is consistent with a unique solution
D) is consistent with two solutions

Solution:
C) is consistent with a unique solution
x + 2y - 5 = 0
2x - 4y + 6 = 0
a1/a2 = 1/2
b1/b2 = 2/-4 = -1/2
c1/c2 = -5/6
a1/a2 ≠ b1/b2 ≠ c1/c2
∴ The lines are consistent and unique solution.

Question 20.
The larger of two supplementary angles exceeds the smaller by 18 degrees. What is the measure of larger angle ?

Solution:
x + y = 180°
x - y = 18°
2x = 198°
x = 198/2 = 99°
y = 180° - 99° = 81°.
Larger angle = 99°.

Question 21.
Assertion (A) : The system of linear equations 3x + 5y - 4 = 0 and 15x + 25y - 25 = 0 is inconsistent.

Reason (R) : The pair of linear equations a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 is inconsistent if a1/a2 = b1/b2 ≠ c1/c2
A) A is true, R is true and R is the correct explanation of A.
B) A is true, R is true but R is not the correct explanation of A
C) A is true, R is false
D) A is false, R is true

Solution:
A) A is true, R is true and R is the correct explanation of A.
3x + 5y - 4 = 0 ;
15x + 25y- 25 = 0
a1/a2 = 3/15 = 1/5
b1/b2 = 5/25 = 1/5
c1/c2 = -4/-25 = 4/25
a1/a2 = b1/b2 ≠ c1/c2
∴ The lines are inconsistent.

Question 22.
What is the angle between two parallel lines ?

Answer:
0°

Question 23.
A line parallel to x + y + 7= 0 is ....... .

A) 2x + 2y + 1 = 0
B) 2x - 2y - 14 = 0
C) x + 3y - 1 = 0
D) 8x - y + 1 = 0

Solution:
A) 2x + 2y + 1 = 0
x + y + 7 = 0 .... (1)
Except constant multiply (1) by 2
2x + 2y + 1 = 0
The lines are parallel.

Question 24.
Identify coincident lines from the following.

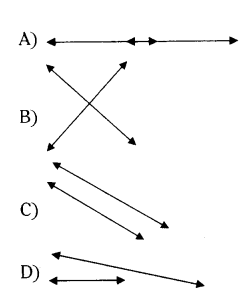
Answer:

Question 25.
"The cost of 1 kg potatoes and 2kg tomatoes was ₹ 30 on a certain day. After two days the cost of 2 kg potatoes and 4 kg tomatoes was found to be ₹ 66".

Read the above information and answer the following questions.
a) Write a pair of linear equations in two variables x and y from the data.

Solution:
x + 2y = 30, 2x + 4y = 66 (or) x + 2y = 33
b) Which system of linear equations in two variables does die data represent?

Solution:
Parallel lines, inconsistent, no solution.

Question 26.
The lines x + 2y + 7 = 0 and 7x + 14y + 49 = 0 are ...... lines.

Solution:
x + 2y + 7 = 0;
7x + 14y + 49 = 0
a1/a2 = 1/7; b1/b2 = 2/14 = 1/7; c1/c2 = 7/49 = 1/7
∴ a1/a2 = b1/b2 = c1/c2
∴ The lines are inconsistent.

Question 27.
a1/a2 = b1/b2 = c1/c2, then the lines are ...... .

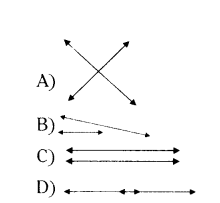
Answer:

Question 28.
Find the area of the triangle formed by the line x/p + y/q = 1 with the co-ordinate axes.

Solution:
Area of triangle
= 1/2 × p × q = pq/2

Question 29.
The two lines x + y = 3, x - y = 1 will intersect at ...... .

A) (2, 1)
B) (-1, 2)
C) (1, 2)
D) (3, 0)

Solution:
A) (2, 1)
x + y = 3
x - y = 1
2x = 4
⇒ x = 2
2 + y = 3
∴ y = 1

Question 30.
The value of m for which the system of equations mx - y = 2 and 6x - 2y - 3 = 0 has a unique solution.

Solution:
mx - y = 2
mx - y - 2 = 0 ... (1)
6x - 2y - 3 = 0 .... (2)
a1/a2 = m/6 b1/b2 = -1/-2 = 1/2 c1/c2 = -2/-3 = 2/3
Unique solution a1/a2 ≠ b1/b2 ≠ c1/c2
m/6 ≠ 1/2
m/3 ≠ 1
m ≠ 3.

Question 31.
The sum of the digits of a two-digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18, then find the number.

Solution:
Let x + y = 12 ... (1)
Number = 10x + y
Interchanged number = 10y + x
10y + x = 10x + y + 18
10x + y + 18 - 10y - x = 0
9x - 9y + 18 = 0
9(x - y + 2) = 0
x - y = -2 .... (2)
(1) + (2) ⇒ 2x = 10 ⇒ x = 5
⇒ y = 12 - 5 = 7 ⇒ y - 7
∴ The number is 57.

Question 32.
For what value of θ, the pair of linear equations x/√2 = y/√2 = 1 and x cos θ + y sin θ = 1 have infinitely many solutions?

Solution:
x/√2 = y/√2 = 1
x cosθ + y sinθ = 1
Infinitely many solutions, a1/a2 = b1/b2 = c1/c2
1/√2cosθ = 1/√2sinθ
cosθ = sinθ
θ = 45°

Question 33.
A line coincident to x/2 + y/3 = 1 is ....... .

A) 6x + y = 4
B) 9x - 3y = 7
C) 9x - y = 1
D) 9x + 6y = 18

Solution:
D) 9x + 6y = 18
x/2 + y/3 = 1
3x + 2y = 6 ... (1)
(1) × 3 ⇒ 9x + 6y = 18

Question 34.
Graphically the pair of equations 7x - y = 5, 21x - 3y = 10 represents two lines which are ...... .

A) parallel
B) intersecting at one point
C) coincident
D) intersecting At two points aj i 1

Solution:
A) parallel
a1/a2 = 7/21 = 1/3
b1/b2 = -1/-3 = 1/3
c1/c2 = 5/10 = 1/2
a1/a2 = b1/b2 ≠ c1/c2
∴ The lines are parallel.

Question 35.
Assertion (A) : If the pair of lines are coincident, then we say that pair of lines is consistent and it has a unique solution. Reason (R): If the pair of lines are parallel, then the pairs has no solution and is called inconsistent pair of equations.
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) Assertion (A) is true, Reason (R) is false.
D) Assertion (A) is false, Reason (R) is true.

Answer:
D) Assertion (A) is false, Reason (R) is true.

Question 36.
Assertion (A) : The lines x + y = 7, 3x - y = 4 are intersecting lines.
Reason (R) : The condition for intersecting lines a1/a2 = b1/b2 ≠ c1/c2
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) Assertion (A) is true. Reason (R) is false.
D) Assertion (A) is false, Reason (R) is true.

Answer:
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.

Question 37.
Assertion (A) : 1 he value of k for which the system of linear equations kx - y = 2 and 6x- 2y = 3 has a unique solution is 3.
Reason (R) : The graph of linear equation a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 given a pair of intersecting
lines, if a1/a2 ≠ b1/b2
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) Assertion (A) is true, Reason (R) is false.
D) Assertion (A) is false. Reason (R) is true.

Answer:
D) Assertion (A) is false. Reason (R) is true.

Question 38.
Assertion (A) : If kx + 2y = 5 and 3x + y = 1 have a unique solution, if k = 6.
Reason (R) : If the lines x + 2y = 3 and 5x + ky + 7 = 0 have unique solution, if k ≠ 1.
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) Assertion (A) is true, Reason (R) is false.
D) Assertion (A) is false, Reason (R) is true.

Answer:
D) Assertion (A) is false, Reason (R) is true.

Question 39.
Assertion (A): If the lines are coincident, then the number of solution is infinite.
Reason (R) : Parallel lines will have 2 solutions.
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) Assertion (A) is true, Reason (R) is true but R is not the correct explanation of A.
C) Assertion (A) is true, Reason (R) is false.
D) Assertion (A) is false, Reason (R) is true.

Answer:
C) Assertion (A) is true, Reason (R) is false.

Question 40.
What is meant by consistent equations? Give example.

Answer:
The pair of Linear equations having at least one solution are called consistent.

Question 41.
For what value of ‘k’, the pair of linear equations 2x - ky + 3 = 0,4x + 6y - 5 = 0 represent parallel lines ?

Solution:
If a1/a2 = b1/b2 ≠ c1/c2 then the equations are parallel lines.
Since 2/4 = -k/6 ≠ 3/-5
⇒ -4k = 12
∴ k = - 3.

Question 42.
Write the equation of the straight line shown in the graph.

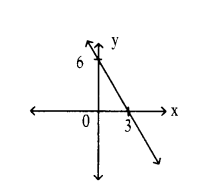
Solution:
Equation of line = x/a + y/b = 1
⇒ x/3 + y/6 = 1 ⇒ = 1
⇒ 2x + y = 6

10th Class Maths Pair of Linear Equations in Two Variables 2 Marks Important Questions

Question 1.
By comparing the ratio a1/a2, b1/b2 and c1/c2 find out whether the lines rep-resenting the following pairs of linear equations intersect at a point or parallel or coincide.

i) 5x - 4y + 8 = 0 and 7x + 6y - 9 = 0.

Solution:
The given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = 5, b₁ = -4, c₁ = 8 and a₂ = 7, b₂ = 6, c₂ = -9
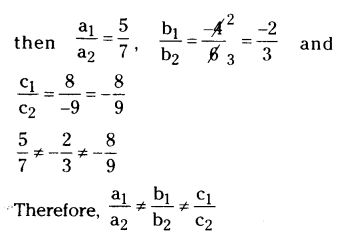Thus the given pair of linear equations can represent the intersecting lines. They can intersect at an unique point. So, they are consistent pair of linear equations.

ii) 2x - 5y + 7 = 0 and 6x - 15y + 21 = 0.

Solution:
The given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = 2, b₁ = -5, c₁ = 7 and a₂ = 6, b₂ = -15, c₂ = 21
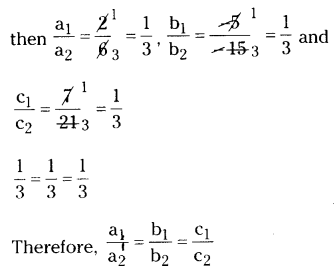Thus the given pair of linear equations are coincident lines and they have infi¬nitely many solutions,

iii) x + 2y - 4 = 0 and 2x + 4y - 12 = 0.

Solution:
The given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = 1, b₁ = 2, c₁ = -4 and a₂ = 2, b₂ = 4, c₂ = -12
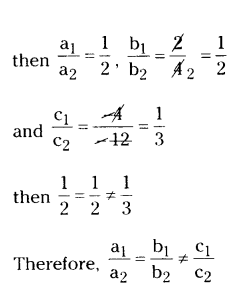Thus the given pairs of linear equations will represent the parallel lines.

Question 2.
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160. After a month, the cost of 4 kg of apples and 2 kg of grapes is f 300. Represent the situation algebraically.

Solution:
Let the cost of 1 kg apples ₹ x and cost of 1 kg of grapes ₹ y
then cost of 2 kg of apples + cost of 1 kg of grapes = ₹ 160
2x + 1y = 160
Cost of 4 kg of apples + cost of 2 kg of grapes = ₹ 300
4x + 2y = 300
Therefore, equations are 2x + y = 160 and 4x + 2y = 300.

Question 3.
Find the values of a and b for which the following system of linear equations has infinite number of solutions. 2x + 3y = 7 and 2ax + (a + b)y = 28 has
i) a unique solution
ii) no solution.

Solution:
Given linear equations are 2x + 3y = 7 and 2ax + (a + b)y = 28
They have infinite number of solutions.
2x + 3y - 7 = 0 and 2ax + (a + b)y - 28 = 0
The given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = 2, b₁ = 3, c₁ = -7 and a₂ = 2a, b₂ = (a + b), c₂ = -28
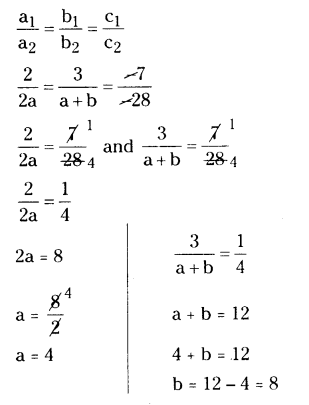∴ a = 4 and b = 8.

Question 4.
Find the value of k for which the following system of equations has no solution.

kx - 5y = 2
6x + 2y = 7

Solution:
The given lines kx - 5y - 2 = 0
6x + 2y - 7 = 0 have no solution.
Given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = k, b₁ = -5, c₁ = -2 and a₂ = 6, b₂ = 2, c₂ = -7
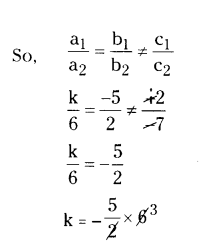∴ k = -15.

Question 5.
For what values of p, the system of equations px + 3y = p - 3 and 12x + py = p will have no solution ?

Solution:
Given linear equations are
px + 3y = p - 3 and 12x + py = p
px + 3y - (p - 3) = 0 and 12x + py - p = 0
have no solution.
Given lines as a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = p, b₁ = 3, c₁ = -(p - 3) and a₂ = 12,
b₂ = p, c₂ = -p
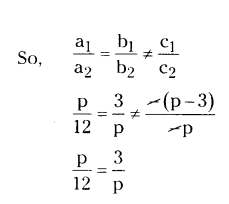p² = 3 × 12 ⇒ p² = 36 ⇒ p = ± 6.

Question 6.
37 pens and 53 pencils together cost ₹ 320, while 53 pens and 37 pencils together cost ₹ 400. Represent the given information in the form of linear equations.

Solution:
Let the cost of pen be ₹ x and pencil be ₹ y
Then cost of 37 pens + cost of 53 pencils = ₹ 320
37x + 53y = 320
Cost of 53 pens + cost of 37 pencils = ₹400
53x + 37y = 400
Therefore linear equations are
37x + 53y = 320 and
53x + 37y = 400.

Question 7.
2 tables and 3 chairs together cost ₹ 2000 where as 3 tables and 2 chairs together cost ₹ 2500 then write the given information in the general form of linear equation form.

Solution:
Let the cost of table be ₹ x and chair be ₹ y.
Then cost of 2 tables + cost of 3 chairs = ₹ 2000
2x + 3y = 2000
Cost of 3 tables + cost of 2 chairs = ₹ 2500
3x + 2y = 2500
Therefore linear equations are
2x + 3y = 2000 and
3x + 2y = 2500.

Question 8.
Write the number of solutions of the following pair of linear equations.

x + 2y - 8 = 0 and 2x + 4y - 16 = 0.

Solution:
Given linear equations are
x + 2y - 8 = 0 and
2x + 4y-16 = 0
The given lines as
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
a₁ = 1, b₁ = 2, c₁ = -8 and a₂ = 2, b₂ = 4, c₂ = -16
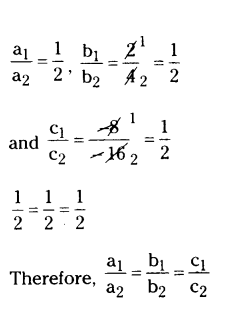Thus the given pair of linear equations can represent the coincident lines. So, they have infinitely many solutions.

Question 9.
Write the number of solutions of the following pair of linear equations :

x + 3y - 4 = 0 and 2x + 6y - 7 = 0.

Solution:
Given linear equations are
x + 3y - 4 = 0 and
2x + 6y - 7 = 0
The given lines as
a₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0
a₁ = 1, b₁ = 3, c₁ = -4 and a₂ = 2, b₂ = 6, c₂ = -7
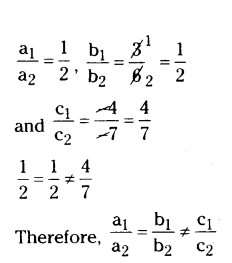Thus the given pair of linear equations can represent the parallel lines. So, they have no solution.

Question 10.
Find whether the following pair of linear equations is consistent or inconsistent.

3x + 2y = 8; 6x - 4y = 9.

Solution:
Given equations are 3x + 2y = 8 and 6x - 4y = 9.
On comparing with a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0 we get
a₁ = 3, b₁ = 2, c₁ = -8
a₂ = 6, b₂ = -4, c₂ = -9
a1/a2 = 3/6 = 1/2
b1/b2 = 2/-4 = -1/2
c1/c2 = -8/-9 = 8/9
a1/a2 ≠ b1/b2 ≠ c1/c2
∴ The lines are inconsistent.

Question 11.
For what values of k will the following pair of linear equations have infinitely many solutions ?

kx + 3y - (k - 3) = 0; 12x + ky - k = 0

Solution:
Given equations are kx + 3y - (k - 3) = 0 12x + ky - k = 0
Here a₁ = k, b₁ = 3, c₁ = -(k - 3) = - k + 3
a₂ = 12, b₂ = k, c₂ = -k.
Infinitely many solutions, the condition is
a1/a2 = b1/b2 = c1/c2
k/12 = 3/k = -(k-3)/-k

⇒ k/12 = 3/k
⇒ k² = 36
⇒ k = √36
⇒ k = ± 6

3/k = -(k-3)/-k
⇒ -3 = -k + 3
⇒ k = 3 + 3
⇒> k = 6
∴ k = 6 only.

Question 12.
For what value of p will the following pair of linear equations have infinitely many solution

(p - 3)x + 3y - p
px + py = 12

Solution:
Given equations are (p - 3) x + 3y = p
px + py = 12
here
a₁ = p - 3, b₁ = 3, c₁ = -p
a₂ = p, b₂ = p, c₂ = -12
infinitely many solutions, the condition is
a1/a2 = b1/b2 = c1/c2 ⇒ p-3/p = 3/p = -p/-12
Here
p-3/p = 3/p
⇒ p - 3 = 3 ⇒ p = 3 + 3
∴ P = 6.

Question 13.
Find the values(s) of k for which the pair of linear equations kx + y = k² and x + ky = 1 have infinitely many solutions.

Given equations are kx + y = k²; x + ky = 1.
a₁ = k, b₁ = 1, c₁ = -k²
a₂ = 1, b₂ = k, c₂ = -1
Infinitely many solution, then the condition is
a1/a2 = b1/b2 = c1/c2
⇒ k/1 1/k = -k2/-1
here k/1 1/k ⇒ k² = 1 ⇒ k = √1 = ±1.

Question 14.
Solve for x and y : x + y = 6, 2x - 3y = 4.

Solution:
Given equations are
x + y = 6 .... (1)
2x - 3y = 4 ... (2)

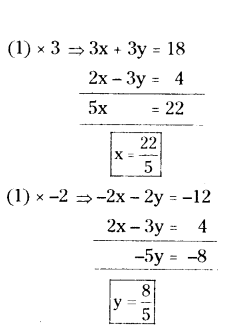
Question 15.
Find out whether the following pair of linear equations are consistent or inconsistent:

5x - 3y = 11, -10x + 6y = 22.

Solution:
Given equations are 5x - 3y = 11
-10x + 6y = 22
a₁ = 5, b₁ = -3, c₁ = -11
a₂ = -10, b₂ = 6, c₂ = -22
a1/a2 = 5/-10 = 1/-2
b1/b2 = -3/6 = 1/-2
c1/c2 = -11/-22 = 1/2
here a1/a2 = b1/b2 ≠ c1/c2
∴ The lines are inconsistent.
∴ These are parallel lines.

Question 16.
Is the system of linear equations 2x + 3y - 9 = 0 and 4x + 6y - 18 = 0 consistent ? Justify your answer.

Solution:
Given equations are 2x + 3y - 9 = 0 and 4x + 6y - 18 = 0
here a₁ = 2, b₁ = 3, c₁ = -9
here a₂ = 4, b₂ = 6, c₂ = -18
a1/a2 = 2/4 = 1/2
b1/b2 = 3/6 = 1/2
c1/c2 = -9/-18 = 1/2
here a1/a2 = b1/b2 = c1/c2
∴ The lines are consistent.
∴ The lines are coincidenl lines.

Question 17.
Given the linear equation 3x + 4y = 9. Write another linear equation in these two variables such that the geometrical representation of the pair if so formed is
i) intersecting lines
ii) coincident lines.

Solution:
Given equation 3x + 4y = 9.
a₁ = 3, b₁ = 4, c₁ = -9.
i) Condition for intersecting lines
a1/a2 ≠ b1/b2 ≠ c1/c2
Intersecting lines : 3x - 4y = 1

ii) Condition for coincident lines
a1/a2 ≠ b1/b2 ≠ c1/c2
∴ Coincident line is 6x + 8y = 18.

Question 18.
Find the value of k so that the pair of equations x + 2y = 5 and 3x + ky + 15 = 0 has a unique solution.

Solution:
Given equations are x + 2y = 5 and 3x + ky + 15 = 0
a₁ = 1, b₁ = 2, c₁ = -5
a₂ = 3, b₂ = k, c₂ = 15
Unique solution,
a1/a2 ≠ b1/b2
1/3 = 2/k
∴ k ≠ 6
Except k = 6, all other values will be the value of k.

Question 19.
In the below figure PQRS is a rectangle. Find x and y.

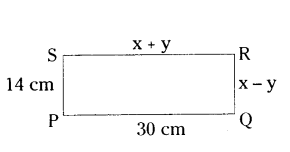
Solution:
PQRS is a rectangle

Question 20.
6 pencils and 4 pens together cost ₹ 50 whereas 5 pencils and 6 pens together cost ₹ 46. Express the above statements in the form of Linear equations.5

Solution:
Let cost of each pencil = ₹ x
∴ Cost of 6 pencils = 6 × ₹ x
= ₹ 6x
∴ Cost of 5 pencils =5 × ₹x
= ₹ 5x
Let cost of each pen = ₹ y
∴ Cost of 4 pens = 4 × ₹y
= ₹ 4y
∴ Cost of 6 pens = 6 × ₹ y
= ₹ 6y
Hence by problem
∴ 6x + 4y = 50
5x + 6y = 46

10th Class Maths Pair of Linear Equations in Two Variables 4 Marks Important Questions

Question 1.
Solve :
2x - y = 4
y - z = 6
x - z = 10

Solution:
Given
2x - y = 4 → (1)
y - z = 6 → (2)
x - z = 10 → (3)
z = x - 10 → (4)
Put (4) in (2)
y- (x- 10) = 6
y - x + 10 = 6
-x + y = 6 - 10
-x + y = -4 → (5)
By adding (1) and (5)
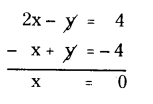∴ x = 0
Put x = 0 in (1)
2(0) - y = 4
-y = 4
y = -4
Put y = -4 in (2)
-4 - z = 6
-z = 6 + 4 = 10
z = -10
Therefore, x = 0, y = -4 and z = -10

Question 2.
Solve the linear equations by substitution method :
a) x + 2y + 1 = 0 and 2x - 3y - 12 = 0

Solution:
Given linear equations are
x + 2y = -1
x = -1 - 2y → (1)
and 2x - 3y = 12 → (2)
Put (1) in (2)
2(-1 - 2y) - 3y = 12
-2 + 4y - 3y = 12
-2 + y = 12
y = 12 + 2 = 14
∴ y = 14
Put y = 14 in (1)
x = -1 - 2(14) = -1 - 28
x = -29
Therefore, x = -29 and y = 14.

b) x/a = y/b and ax + by = a² + b².

Solution:
Given linear equations are
x/a = y/b
x = ay/b → (1)
and ax + by = a² + b² → (2)
and Put (1) in (2)
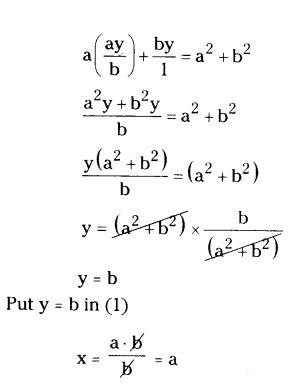Therefore, x = a and y = b.

Question 3.
For what value of k will the following system of linear equations has no solution ?
3x + y = 1 and (2k - 1)x + (k - 1)y = 2k + 1

Solution:
Given linear equations are 3x + y = 1 and (2k - 1)x + (k - 1)y = 2k + 1
3x + y - 1 = 0 and (2k - 1)x + (k - 1)y - (2k + 1) = 0
are in the form of a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0
a₁ = 3, b₁ = 1, c₁ = -1 and a₂ = 2k - 1, b₂ = k - 1, c₂ = -(2k + 1) they have no solution
That is a1/a2 = b1/b2 ? c1/c2
So, 3/2k-1 = 1/k-1
3(k - 1) = 1 (2k - 1)
3k - 3 = 2k - 1
3k - 2k = -1 + 3
∴ k = 2

Question 4.
Determine the value of k so that the following linear equations have no solution :
(3k + 1) x + 3y - 2 = 0 and (k² + 1) x + (k - 2) y - 5 = 0.

Solution:
Given linear equations are
(3k + 1) x + 3y - 2 = 0
and (k² + 1) x + (k - 2) y - 5 = 0
are as in a₁x + b₁y + c₁ = 0
and a₂x + b₂y + c₂ = 0
a₁ = 3k + 1, b₁ = 3, c₁ = -2 and a₂ = k² + 1, b₂ = k - 2, c₂ = -5
Give equations have no solution

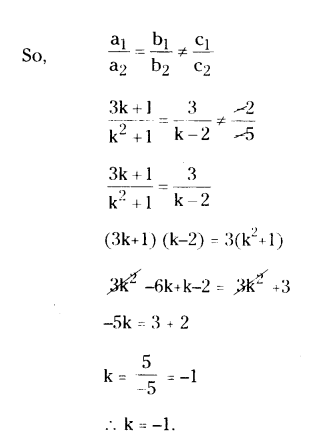
Question 5.
Find the value of a and b for which the following system of linear equa¬tions has infinite number of solutions: 2x - 3y = 7 and (a + b)x - (a + b - 3)y = 4a + b.

Solution:
Given linear equations has infinite number of solutions.

2x - 3y = 7
⇒ 2x - 3y - 7 = 0
and (a + b)x - (a + b - 3)y = 4a + b
and (a + b)x - (a + b - 3)y - (4a + b) = 0
are as in a₁x + b₁y + c₁ = 0
and a₂x + b₂y + c₂ = 0
a₁ = 2, b₁ = -3, c₁ = -7 and a₂ = a + b, b₂ = -(a + b - 3), c₂ = -(4a + b)
So, a1/a2 = b1/b2 = c1/c2
2/a+b = -3/-(a+b-3) = -7/-(4a+b)
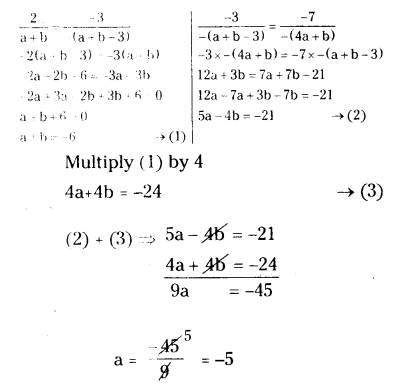Put a = -5 in (1)
-5 + b = -6
b = -6 + 5 = -1
∴ a = -5 and b = -1.

Question 6.
The sum of two numbers is 8. If their sum is four times their difference. Express the information is linear equations.

Solution:
Let the numbers be x and y.
Sum of two numbers = 8
x + y = 8
Sum of two numbers = 4 times of difference of two numbers
x + y = 4(x - y)
x + y = 4x - 4y
4x - 4y - x - y = 0
3x - 5y = 0
Therefore, linear equations are x + y = 8 and 3x - 5y = 0.

Question 7.
The sum of digits of a two digit number is 13. If the number is subtracted from the one obtained by interchanging the digits. The result is 45. Express it as the linear equations.

Solution:
Let the tens digit and ones digit are x and y respectively.
Their sum is 13 that is x + y = 13
Then number = 10x + 1y
If digits reversed then number = 10y + 1x
Reversed number - Number = 45
10y + x - 10x - y = 45
9y - 9x = 45
9(y - x) = 45
y - x = 45/9 = 5
x - y + 5 = 0
Therefore linear equations are
x + y = 13
x - y = -5.

Question 8.
The father is three times as old as his son. After twelve years his age will be twice as that of his son. Express it in as equations.

Solution:
Let the present ages of father and son are x and y respectively.
Then father’s age = 3 times of son’s age
x = 3y
x - 3y = 0
After 12 years father’s age = x + 12
son’s age = y + 12
then father’s age = 2 times of son’s age
x + 12 = 2(y + 12)
x + 12 = 2y + 24
x - 2y = 24 - 12
x - 2y = 12
Therefore linear equations are
x - 3y = 0 and
x - 2y = 12.

Question 9.
If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes 1/2 if we only add 1 to the denominator. What is the fraction ?

Solution:
Let the fraction be x/y.
x +1
Case (i) : x+1/y-1 = 1
⇒ x + 1 = y - 1
⇒ x + 1 - y + 1 = 0
⇒ x - y + 2 = 0 .... (1)

Case (ii) : x/y+1 = 1
2x = y + 1
2x - y - 1 = 0 ... (2)

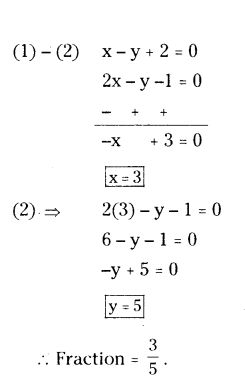
Question 10.
For which value of ‘k’ will the following pair of linear equations have no solution ?

3x + y = 1
(2k - 1) x + (k - 1)y = 2k + 1.

Solution:
Given equations 3x + y = 1 ... (1)
(2k - 1) x + (k - 1) y = 2k + 1 ... (2)
a₁ = 3, b₁ = 1, c₁ = -1
a₂ = 2k - 1, b₂ = k - 1, c₂ = -2k - 1
No solution, a1/a2 = b1/b2 ≠ c1/c2
3/2k-1 = 1/k-1
3k - 3 = 2k - 1
3k - 2k = -1 +3
∴ k = 2

Question 11.
If 2x + y = 23 and 4x - y = 19, find the value of (5y - 2x) and (y/x - 2)

Solution:
Given equations are 2x + y = 23 ... (1)
4x - y = 19 .... (2)

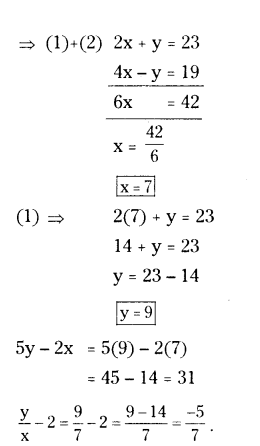
Question 12.
A lending library has a fixed charge for first three days and an additional charge for each day thereafter. Rithik paid ₹ 27 for a book kept for 7 days and Manmohan paid ₹ 21 for a book kept for 5 days. Find the fixed charges and the charge for each extra day.

Solution:
Let the fixed charge be ₹ x.
Let the extra charge be ₹ y.
x + 4y = 27 ... (1)
x + 2y = 21 ... (2)
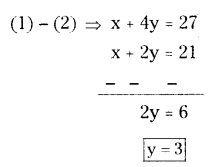(1) ⇒ x + 4(3) = 27
x + 12 = 27
x = 27 - 12
x = 15
∴ Fixed charge = ₹ 15
Charge for extra day = ₹ 3.

Question 13.
Solve the pair of equations graphically 4x - y = 4; 3x + 2y = 14.

Solution:
4x - y = 4; 3x + 2y = 14

x	0	2	1
y	-4	4	0

x	0	4	2
y	7	1	4

(0, -4), (2, 4). (1, 0) (0, 7), (4, 1) (2, 4)
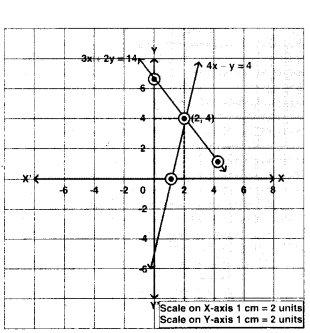From the graph
The two lines will intersect at (2, 4).
Solution x = 2, y = 4.

Question 14.
Determine the values of m and n, so that the following system of linear equation has infinite number of solutions.

(2m - 1)x + 3y - 5 = 0
3x + (n - 1) y - 2 = 0.

Solution:
Given equations are (2m - 1) x + 3y - 5 =, 0
3x + (n - 1) y - 2 = 0
a₁ = 2m - 1, b₁ = 3, c₁ = -5
a₂ = 3, b₂ = n - 1 c₂ = -2

Question 15.
Solve : x + y = a + b
ax - by = a² - b².

Solution:
Given equations are x + y = a + b .... (1)
ax - by = a² - b² .... (2)
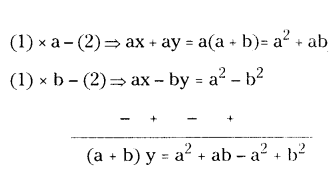(a + b) y = ab + b²
(a + b)y = b(a + b)
y = (a+b)b/a+b
y = b
(1) ⇒ x + ba + b
x = a
∴ Solution (x, y) = (a, b).

10th Class Maths Pair of Linear Equations in Two Variables 8 Marks Important Questions

Question 1.
Draw the graphs of 2x + y = 6 and 2x - y + 2 = 0. Shade the region bounded by these lines and x-axis. Find the area of the shaded region.

Answer:
2x + y = 6
y = 6 - 2x
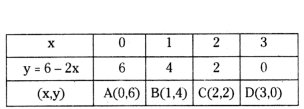2x - y + 2 = 0
y = 2x + 2
So, from the graph vertices of the ΔBTD are B(1, 4), T(-1, 0) and D(3, 0).
If BM ⊥ TD then BM = 4 units
Length of TD = 4 units
Area of triangle BTD
= 1/2 × base × height = 1/2 × TD × BM
= 1/2 × 4 × 4 = 8 sq. units
So, area of the triangle is 8 sq. units.

Question 2.
Solve the following linear equations graphically 4x - 5y - 20 = 0 and 3x + 5y - 15 = 0. Determine the vertices of the triangle formed by the lines representing the above equation and the Y-axis.

Solution:
4x - 5y - 20 = 0
5y = 4x - 20
y = 4x-20/5
3x + 5y - 15 = 0
5y = -3x + 15
y = -3x+15/5
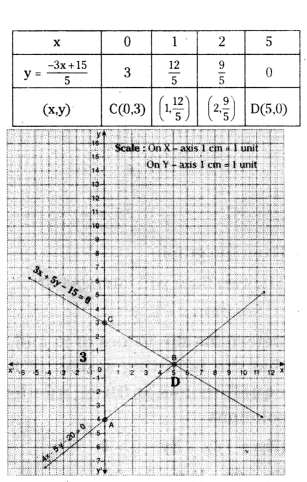From the graph vertices of the ΔABC are A(0,-4), B(5,0) and C(0,3).
Draw BM ⊥ AC then BM = 5 units and AC = 7 units
Area of the triangle ABC
= 1/2 × base × height
= 1/2 × AC × BM
= 1/2 × 7 × 5 = 35/2
Therefore area of triangle ABC = 17.5 sq. units.

Question 3.
Solve : 1/2(2x+3y) + 1/27(3x-2y) = 1/2 7/2x+3y + 4/3x-2y = 2 where
(2x + 3y) ≠ 0 and 3x - 2y ≠ 0.

Solution:
Given linear equations are
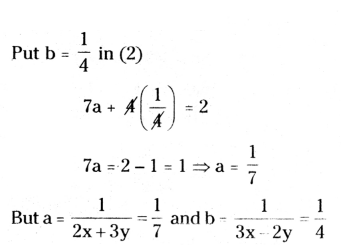2x + 3y = 7 → (3) and 3x - 2y - 4 → (4)
To equate the x coefficients.
(3) × 3 and (4) × 2
3(2x + 3y) = 3 × 7
6x + 9y = 21 → (5)
2(3x - 2y) = 2 × 4
6x - 4y = 8 → (6)
Subtract (6) from (5)
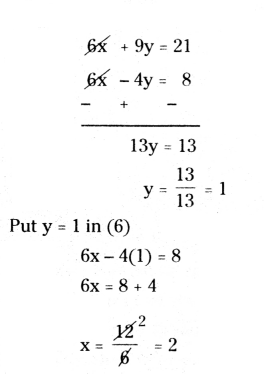Therefore x = 2 and y = 1.

Question 4.
Solve the linear equations 5/x-1 + 1/y-2 = 2 and 6/x-1 - 3/y-2 = 1.

Solution:
Given linear equations are
5/x-1 + 1/y-2 = 2 and 6/x-1 - 3/y-2 = 1.
Let 1/x-1 = a and 1/y-2 = b
then 5a + b = 2 ⇒ b = 2 - 5a → (1)
and 6a - 3b = 1 → (2)
Put (1) in (2)
6a - 3(2 - 5a) = 1
6a - 6 + 15a = 1
21a = 1 + 6 = 7
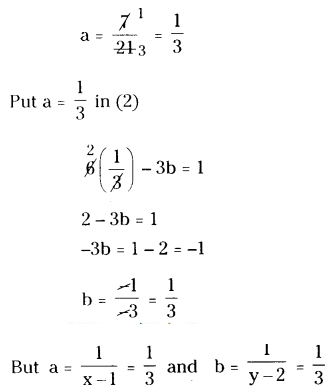x - 1 = 3
x = 3 + 1 = 4

y - 2 = 3
y = 3 + 2 = 5
Therefore, x = 4 and y = 5.

Question 5.
Aditya has pens and pencils which together are 40 in number. If he had 5 more pencils and 5 less pens, then the number of pencils would become 4 times the number of pens. Find the original number of pens and pencils.

Let the number of pens and pencils are x and y respectively.
x + y = 40 → (1)
If 5 more pencils and 5 less pens
Pencils = 4 times of pens
y + 5 = 4(x - 5)
y + 5 = 4x - 20
4x - y = 25 → (2)
By adding (1) and (2)
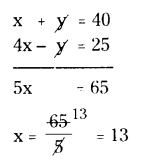Put x = 13 in (1)
13 + y = 40
y = 40 - 13 = 27
Therefore, number of pens x = 13
Number of pencils y = 27.

Question 6.
A two-digit number is 4 more than 6 times the sum of the digits. If 18 is subtracted from the number, the digits are reversed. Find the number.

Solution:
Let the tens and ones place digits are x and y respectively. Then number = 10x + 1y = 10x + y
Number = 6 times of sum + 4
10x + y = 6(x + y) + 4
10x + y = 6x + 6y + 4
10x - 6x + y - 6y = 4
4x - 5y = 4 → (1)
Number - 18 = reversed number
10x + y - 18 = 10y + x
10x - x + y - 10y = 18
9x - 9y = 18
9(x - y) = 18
x - y = 18/9 = 2
x - y = 2 → (2)
To equate the coefficients of x multiply (2) by 4
4x - 4y = 8 → (3)
Subtract (3) from (1)
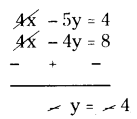Put y = 4 in (2)
x - 4 = 2
x = 2 + 4 = 6
Then the number
= 10 × 6 + 1 × 4 = 60 + 4 = 64.

Question 7.
The sum of the numerator and denominator of a fraction is 4 more than twice the numerator. If the numerator and denominator are increased by 3, they are in the ratio 2 : 3. Determine the fraction.

Solution:
Let the numerator and denominator of a fraction are x and y respectively.
Numerator + Denominator = twice of numerator + 4
x + y = 2x + 4;
2x - x - y + 4 = 0
x - y = -4 → (1)
If numerator and denominator increased by 3 then x+3/y+3 = 2/3
3(x + 3) = 2(y + 3)
3x + 9 = 2y + 6
3x - 2y = 6 - 9 = -3
3x - 2y = -3 → (2)
To equate the y-coefficients multiply (1) by 2
2x - 2y = -8 → (3)
Subtract (3) from (2)
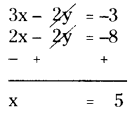Put x = 5 in (1)
5 - y = -4
-y = -4 - 5 = -9
∴ y = 9
Therefore, fraction = x/y = 5/9.

Question 8.
The ages of two friends Aditya and Kishore differ by 3 years. Aditya’s father Siva Prasad is twice as old as Aditya and Kishore is twice as old as his sister Swathi. The ages of Swathi and Siva Prasad differ by 30 years. Find the ages of Aditya and Kishore.

Solution:
Let Aditya and Kishore ages are x and y respectively, then x - y = 3 → (1)
Let the ages of Siva Prasad and Swathi’s are a and b respectively,
then age of Siva Prasad = 2 of Aditya
a = 2x → (2)
Age of Kishore = twice of Swathi’s age
y = 2b
b = y/2 → (3)
Siva Prasad age - Swathi’s age = 30
a - b = 30 → (4)
Put (2) and (3) in (4)
2x/1 - y/2 = 30 4x-y/2 = 30
4x - y = 60 → (5)
Subtract (1) from (5)
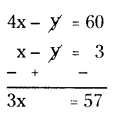x = 57/3 = 19
Put x = 19 in (1) ⇒ 19 - y = 3
⇒ -y = 3 - 19
⇒ -y = -16
⇒ y = 16
Therefore, Aditya’s age (x) = 19 years
and Kishore’s age (y) = 16 years

Question 9.
Points A and B are 70 km, a part on a highway. A car starts from A and another car starts from B simultaneously. If they travel in the same directions they meet in 7 hours, but if they travel towards each other, they meet in one hour. Find the speed of the two cars.

Solution:
Let speed of car A is x kmph and car B is y kmph.
The distance between two cars = 70 km. If they are moving in the same direction they can meet at Q after 7 hours. So, t = 7 hours,
distance - speed × time
Then distance travelled by car A = 7x
distance travelled by car B = 7y
distance - B distance = 70 km
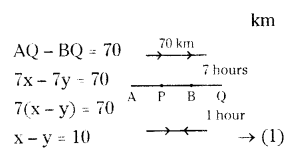If they are moving in opposite direction then can meet at P.
Then distance travelled by car A = 1x
distance travelled by car B = 1y
AP + PB = 70
x + y = 70 → (2)
By adding (1) and (2)
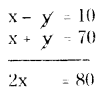x = 80/2 = 40
Put x = 40 in (2)
40 + y = 70
y = 70 - 40 = 30
speed of car A (x) = 40 kmph
Speed of car B (y) = 30 kmph.

Question 10.
If in a rectangle, the length is increased and breadth reduced each by 2 units, the area is reduced by 28 sq. units. If however the length is reduced by 1 unit and the breadth increased by 2 units, the area increases by 33 sq. units. Find the area of the rectangle.

Solution:
Let l and b are length and breadth of a rectangle. Then it area = l.b
If length increased by 2 and breadth reduced by 2
then (l + 2) (b - 2) = area - 28
lb - 2l + 2b - 4 = lb - 28
-2l + 2b = -28 + 4
-2l + 2b = -24 → (1)
If length decreased by 1 and breadth increased by 2
then (l - 1) (b + 2) = area + 33
lb + 2l - b - 2 = lb + 33
2l - b = 33 + 2
2l - b = 35 → (2)
By adding (1) and (2)
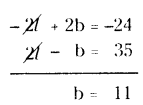Put b = 11 in (2)
2l - 11 = 35
2l = 35 + 11 = 46
l = 46/2 = 23
Therefore, length and breadth of rectangle are 23 units and 11 units.

Question 11.
A two-digit number is obtained by either multiplying the sum of the digits by 8 and then subtracting 5 or by multiplying the difference of the digits by 16 and then adding 3. Find the number.

Solution:
Let the digit One’s place = x.
Let the digit in Tens place = y
∴ Number = 10y + x
∴ 10y + x = 8(x + y) - 5 .... (1)
10y + x = 16(y - x) + 3 .... (2)
(1) ⇒ 10y + x = 8x + 8y - 5
⇒ 8x + 8y - 5 - 10y - x = 0
⇒ 7x - 2y - 5 = 0 ... (3)
(3) × 3 ⇒ 21x - 6y = 15 ... (4)
(2) ⇒ 10y + x = 16y - 16x + 3
⇒ 17x - 6y = 3 .... (5)
(4) - (5) ⇒ 4x = 12
x = 3
(4) ⇒ 21(3) - 6y = 15
63 - 6y = 15
63 - 15 = 6y
48 = 6y
y = 8
∴ Number = 83.

Question 12.
A two-digit number is such that the product of its digits is 8. When 18 is subtracted from the number; the digits interchange their places. Find the number.

Solution:
Let the two digit number be 10x + y.
xy = 8 ..... (1)
10x + y - 18 = 10y + x
9x - 9y - 18 = 0
x - y = 2
x = 2 + y .... (2)
(1) ⇒ (2 + y) y = B
⇒ y² + 2y = 8
⇒ y² + 4y - 2y - 8 = 0
⇒ y(y + 4) - 2(y + 4) = 0
⇒ (y + 4) (y - 2) = 0
∴ y = -4 or 2
(2) ⇒ x = 2 + 2 = 4
∴ The two digit number = 10(4) + 2 = 42

Question 13.
The difference of square of two numbers is 180. The square of the smaller number is 8 times the larger number. Find the number.

Solution:
Let x and y be the larger and smaller numbers respectively.
∴ x² - y² = 180 ... (1)
y² = 8x .... (2)
∴ x² - 8x = 180
x² - 8x - 180 = 0
x² - 18x + 10x - 180 = 0
x(x - 18) + 10(x - 18) = 0
(x - 18) (x + 10) = 0
x - 18 = 0 (or) x + 10 = 0
x = 18 (or) x = -10
∴ x = 18 only
y² = 8x = 8 × 18 = 144
y = √144
y = ±12
∴ The numbers are 18 and 12 or 18 and -12.

Question 14.
A lab assistant has the solution of 50% acid and other which has 25% acid, how much of each should be mixed to make 10 litres of 40% solution ?

Solution:
Let ‘x’ be the amount of 50% acid solution.
‘y’ be the amount of 25% acid solution,
∴ x + y = 10
y = 10 - x ... (1)
50% = 0.5 and 25% = 0.25, 40% = 0.4
0.5x + 0.25y = 0.4 (10)
0.5x + 0.25 (10 - x) = 4 (by (1))
0.5 x + 2.5 - 0.25x = 4
0.25x = 4 - 2.5
0.25x = 1.5
x = 1.5/0.25
x = 150/25
x = 6
(1) ⇒ y = 10 - 6
y = 4
∴ Required amount of solution of acid to make a 40% acid solution will be
for 50% = 6 litres
for 25% = 4 litres.

Question 15.
Solve : (a + 2b) x + (2a - b) y = 2; (a - 2b) x + (2a + b) y = 3.

Solution:
Given equations are
(a + 2b) x + (2a - b) y = 2 ... (1)
(a - 2b)x + (2a + b) y = 3 0) .... (2)
(1) + (2) ⇒ 2ax + 4ay = 5
⇒ 2x + 4y = 5/a ..... (3)
(1) - (2) ⇒ 4bx - 2by = -1
⇒ 4x - 2y = -1/k ..... (4)
(3) × (2) - (4) ⇒ 2(2x + 4y) - (4x - 2y)
= 10/a + 1/b
⇒ 10y = 10/a + 1/b
1/a + 1/10b

Question 16.
Solve : ax + by = a²; bx + ay = b².

Solution:
Given equations are ax + by = a² ...... (1)
bx + ay = b² ..... (2)

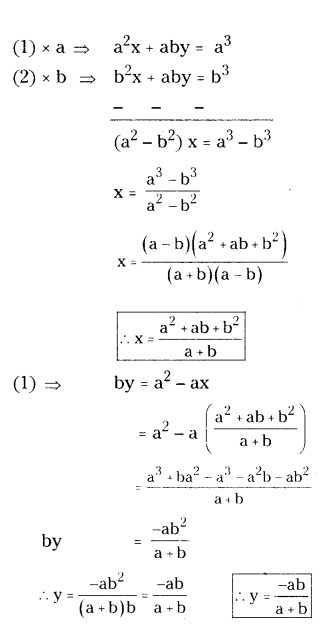
AP 10th Class Maths 4thLesson Important Questions and Answers Pair of Linear Equations in Two Variables

Question 1.
What is meant by consistent equations ? Give example.

Solution:
The pair of Linear equations having at least one solution are called consistent.

Question 2.
Find the value of ‘k’ for which the sys-tem of equations x + 2y - 3 = 0 and 5x + ky + 7 = 0 has no solution.

Solution:
Find the value of ’k’ for which the system of equations x + 2y - 3 = 0 and 5x + ky + 7 = 0 has no solutions.
They have no solution means they are parallel.
a₁x + b₁y + c₁ = 0 and
a₂x + b₂y + c₂ = 0 are parallel if
a1/a2 = b1/b2 ≠ c1/c2 here given
a₁ = 1, b₁ = 2, C₁ = - 3 and a₂ = 5, b₂ = k, c₂ = 7
a1/a2=b1/b2⇒1/5 = 2/k ⇒ k = 5(2) = 10
∴ If k = 10 then the above system will have no solution.

Question 3.
Find the value of k for which the pair of equations 2x + ky + 3 = 0,

4x + 6y - 5 = 0 represent parallel lines.

Solution:
2x + ky + 3 = 0 and 4x + 6y - 5 = 0
∴ a₁ = 2, b₁ = k, C₁ = 3
a₂ = 4, b₂ = 6, c₂ = -5
If the given equations are parallel lines, then
a1/a2 = b1/b2 ≠ c1/c2
Therefore a1/a2 = b1/b2 ≠ c1/c2 ⇒ 4k = 12
⇒ k = 12/4 = 3
∴ k = 3

Question 4.
The larger of two supplementary angles exceeds the smaller by 58°, then find the angles. *19

Solution:
Let supplementary angles be x and y.
x = y + 58° ⇒ x - y = 58° ..... (1)
∵ x + y = 180° .....(2)
By solving (1) and (2)
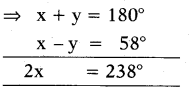∴ x = 119° and y = 180°- 119° - 61°
∴ The angle| are 119° and 61°.

Question 5.
For what value of ‘k’ the pair of linear equations 2x - ky + 3 = 0, 4x + 6y -5 = 0 represent parallel lines ?

Solution:
If a1/a2 = b1/b2 ≠ c1/c2, then the equations are parallel lines.
Since a1/a2 = b1/b2 ≠ c1/c2 ⇒ -4k = 12
∴ k = - 3.

Question 6.
Reduce the pair of equations 2/x+3/y = 1/3 and 5/x+4/y = - 2
(x ≠ 0, y ≠ 0) into a pair of linear equa-tions in two variables ‘a’ and ‘b’.

Solution:
Given equations are 2/x+3/y = 13 .......(1)
and 5/x+4/y = - 2 - (2)
Let 1/x = a and 1/y = b
then the given equations can be writ¬ten as 2a 4- 3b = 13 and 5a + 4b = -2

Question 7.
Write the equation of the straight line shown in the graph.

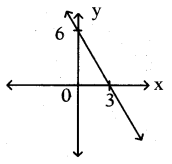
Solution:
Equation of line = x/a+y/b = 1
⇒ x/3+y/6 = 1 ⇒ 2x+y/6 = 1
⇒ 2x + y = 6AP 10th Class Maths Important Questions Chapter 4 Pair of Linear Equations in Two Variables 1

Question 8.
Solve the following equations by sub-stitution method

i) 2x - 7y = 3
ii) 4x + y = 21

Solution:
The given two linear equations are
2x - 7y = 3 ..... (1)
4x + y = 21 ......(2)
From the equation (2) we get
y = 21 - 4x now we substitute this Y value in equation (1)
We get
2x - 7(21 - 4x) = 3
⇒ 2x- 147 + 28 x - 3
⇒ 30 x = 147 + 3 = 150
then x = 150/30 ∴ x = 5
Now put x = 5 in equation (2) we get
4(5) + y = 21
20 + y = 21
y = 21 - 20 = 1
So x = 5 and y = 1 are the solutions of the system.

Question 9.
10 students of 10th class participated in a Quiz programme. The number of girls participated in it is 4 more than boys. So find the number of boys and girls participated in Quiz.

Solution:
Let the number of girls = x (say)
and the number of boys = y (say)
then total students = x + y
-10 ..... (1)
and also
The number of girls = number of boys + 4
x = y + 4 ......(2)
Put this ‘x’ value in equation (1), we get
y + 4 + y = 10
⇒ 2y + 4 = 10
⇒ 2y = 10 - 4 = 6
∴ y = 6/2 = 3
So y = 3 then
x + y = 10 becomes
x + 3 = 10
⇒ x = 10-3
∴ x = 7
So the number of girls = 7 and the number of boys = 3.

Question 10.
Is the pair of linear equations 3x - y = 40, 4x - 2y = 50 consistent or inconsis-tent ? Why ?

Solution:
Given equations are consistent.
Reason : Given equations are 3x - y = 40, 4x - 2y = 50
a1/a2 = 3/4 ; b1/b2=1/2 ; a1/a2 ≠ b1/b2
Hence the linear equations are consis-tent.

Question 11.
"Dependent pair of linear equations in two variables is always consistent". Is it TRUE or FALSE ? Justify.

Solution:
"Dependent pair of linear equations in two variables is always consistent".
This is true because dependent pair of linear equations represent coincident lines which have infinite number of solutions. Hence they are consistent.

Question 12.
Draw a rough diagram (graph) of lin-ear equation x = 2.

Solution:
Linear equation x = k represents a line, which is parallel to Y-axis at a distance of ‘k’ units.
∴ x = 2 can be represented as follows :

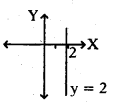
Question 13.
Solve x + 2y = 5 and 2x - y = 0 using any non-graphical method.

Solution:
x + 2y = 5 ..... (1)
2x-y = 0 .... (2)
2x = y ⇒ x = y/2
This value substitute in equation (1)
y/2 + 2y = 5 ⇒ y + 4y = 10
5y = 10 ⇒ y = 2
This value substitute in equation (2)
2x - 2 = 0 ⇒ 2x = 2 ⇒ x = 1
∴ x = 1, y = 2.

Question 14.
Vamsi bought 9 kg of onions and 2 kg of potatoes for Rs. 247. If the cost of 1 kg of onion is Rs. 3 more than that of potatoes, find their cost per kg.

Solution:
Let the cost of 1 kg of potato be x.
Then cost of 1 kg of onion is x + 3
x + x + 3 = 247
2x + 3 = 247
2x = 244 ⇒ x = 244/2 = Rs. 122.
The cost of potatoes per kg = Rs. 122
The cost of onions per kg = x + 3
= 122 + 3 = Rs. 125

Question 15.
Solve the given pair of linear equations by elimination method.

i) 2x + y - 5 = 0 and
ii) 3x - 2y - 4 = 0.

Solution:
In this elimination method, we solve this pair of linear equation by making either of coefficients equal.
The given equations are
2x + y = 5 ......(1)
3x - 2y = 4 .....(2)
To make the coefficients of ‘x’ equal let us multiply the equation (1) by 3 and the equation (2) by (2) on both sides. We get
(2x + y = 5) 3; (3x - 2y = 4) 2
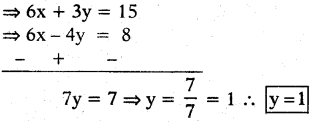then 2x + y = 5 becomes
2x + 1 = 5
⇒ 2x = 5 - 1 = 4
∴ x = 4/2 = 2 So x = 2
x = 2 and y = 1 are the solutions of the given equations.
Verification : Put x = 2 and y = 1 in equation (1) and (2)
2x + y = 5
2(2) + 1 = 5
4 + 1 = 5
5=5
LHS = RHS

3x - 2y = 4
3(2) - 2(1) = 4
6 - 2 = 4
4 = 4
LHS = RHS

Question 16.
Solve the following equations graphically.

1/3 x + 1/2 y = 1; 2x - 1/3 y = - 2/3

Solution:
First we convert above given equations into linear equation form.
So 1/3 x + 1/2 y = 1 can be written as 2x+3y/6 = 1
⇒ 2x + 3y = 6 .... (1)
and 2x + 1/3 y = -2/3 ⇒ 6x-y/3 = - 2/3
⇒ 6x - y = - 2 ...... (2)
now we find the points through which the above lines passes.

i) 2x + 3y = 6 ⇒ y = 6-2x/3
So (0, 2) (3, 0) are two points lie on 2x + 3y = 6

ii) 6x - y = - 2 ⇒ y = 6x + 2
So (0, 2) (1, 8) are two points lie on 6x - y = -2
I’m 5
now we plot a,ove points A(0, 2),
B(3,0) and join ↔AB again÷ve plot (0, 2) (1, 8) and join the line ↔CD . . Now we observe (0, 2) is intersection of two lines.
Hence the solution of given equations = (0, 2)
So x = 0; y = 2 is the solution.

Question 17.
Solve the following pair of equations by eliminating method.

2x + y - 5 = 0; 3x - 2y - 4 = 0

Solution:
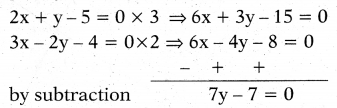substitute y = 1 in 2x + y -5 = 0
2x + 1 - 5 = 0
2x = 4
x = 2

Question 18.
Solve the following pair of linear equations graphically.

2x + y = 4 and 2x - 3y = 12

Solution:
Given equations are
2x + y - 4 = 0 and 2x - 3y - 12 = 0
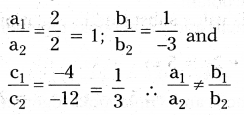The equations are consistent.
∴ They intersect at one point giving only one solution.
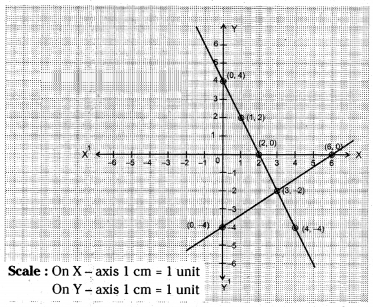From the observing of above graph the solution is x = 3 and y = -2

Question 19.
6 pencils and 4 notebooks together cost Rs. 90/- whereas 8 pencils and 3 note-books together cost Rs. 85/-. Find the cost of one pencil and that of one note-book.

Solution:
Let the cost of each pencil be ₹ x and the cost of each pen be ₹ y.
By problem,
6 pencils and 4 notebooks together cost ₹90.
∴ 6x.+ 4y = 90 ...... (1)
8 pencils and 3 notebooks together cost, ₹85.
∴ 8x + 3y = 85 .....(2)
By solving the eqns (1) and (2)
6x + 4y = 90 ⇒ 3(6x + 4y) = 90 x 3
⇒ 18x + 12y = 270
8x + 3y = 85 ⇒ 4(8x + 3y) = 85 x 4
⇒ 32x + 12y = 340
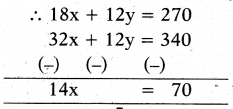x = 5
From (2) ⇒ 8(5) + 3y = 85
⇒ 3y = 85 - 40 = ₹ 45
∴ y = ₹15
∴ Cost of each pencil be = x = ₹ 5
Cost of each pen be = y = ₹ 15

Question 20.
Solve the pair of equations

3/x+y + 2/x-y = 2 and 9/x+y - 4/x-y = 1

Solution:
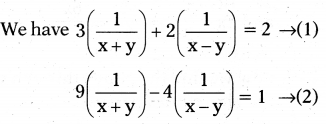If we substitute 1/x+y = p and 1/x-y = q
We get the following pair of linear equations
3p + 2q = 2 .......(3)
9p - 4q = 1 ........(4)
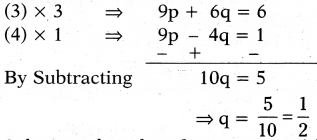Substitute the value of q in equation (3)
3p + 2(1/2) = 2
⇒3p + 1 = 2 ⇒ 3p = 1
P = 1/3
But 1/x+y = p = 1/3 x + y = 3 ...... (5)
1/x-y = q = 1/2 x - y = 2 ..... (6)
By solving (5) and (6)

Question 21.
Solve the following pair of linear equations graphically.
2x-3y + 13 = 0, 3x-2y + 12 = 0

Solution:
Given equations are 2x - 3y + 13 = 0 and 3x - 2y + 12 = 0
i.e., 2x - 3y = - 13 and 3x - 2y = - 12
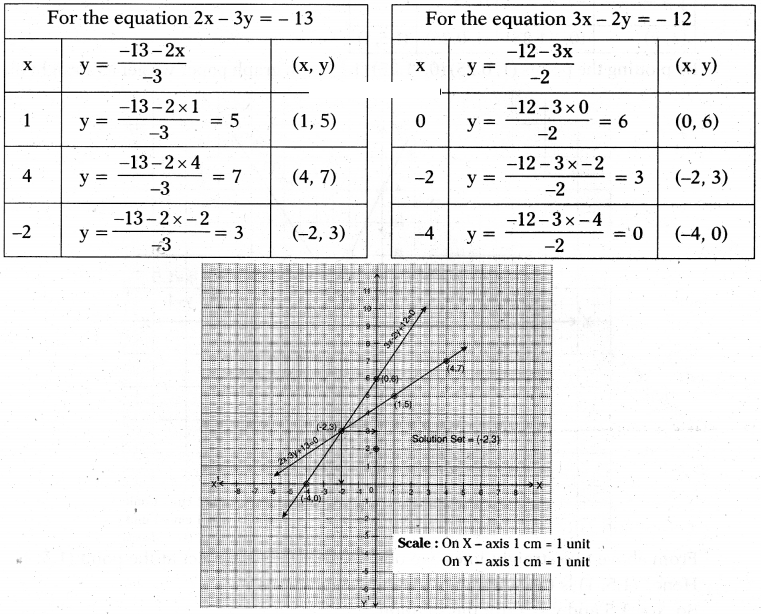The unique solution of this pair of equations = (-2, 3)

Question 22.
Solve the equations 2x + y = 4 and 3x - 2y = 5/2 graphically.

Solution:
To solve the equations
2x + y = 4 and 3x - 2y = 5/2 graphically
We can rewrite the given equations as follows
2x + y = 4 ⇒ y = 4 - 2x ..... (1)
3x - 2y = 5/2 ⇒ 6x-4y = 5 ⇒ y = 6x-5/4
Now we choose the co-ordinates of the points lie on the straight lines represented by above (1) & (2)
So we plot the points (0, 4), (1, 2), (2, 0) and (1.5, 1) on graph paper and connect them to get its straight line and
By plotting the points (1, 0.25) (0, -1.25) (1.5, 1) on graph paper we get its straight line.
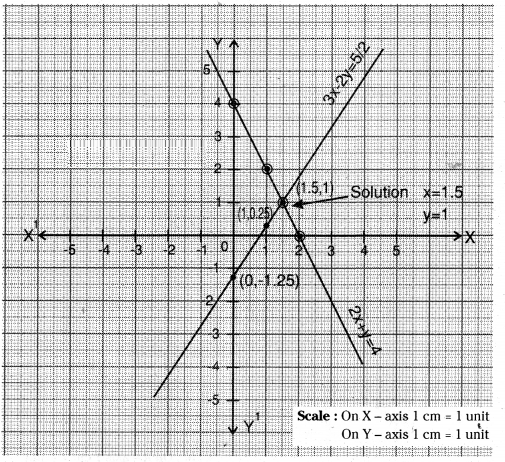From above two straight lines, we observe that they intersect at the point (1.5, 1). Hence (1.5, 1) is the solution of given two equations So, x = 1.5 and y = 1 are the solution.

Question 23.
Solve the pair of equations by reduc¬ing them to a pair of linear equations.

5/(x+y) - 2/(x-y) = -1
15/x+y - 7/x-y = -10, where x ≠ 0 and y ≠ 0

Solution:
Given 5/(x+y) - 2/(x-y) = -1 and
15/x+y - 7/x-y = -10
Take 1/x+y = a and 1/x-y = b, then the given equations reduce to
5a - 2b = - 1 .... (1)
15a - 7b = - 10 .....(2)
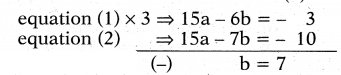∴ b = 7
Substituting b = 7 equation (1)
we get
5a - 2(7) = - 1 ⇒ 5a = - 1 + 14
⇒ 5a = 13 ⇒ a = 13/5

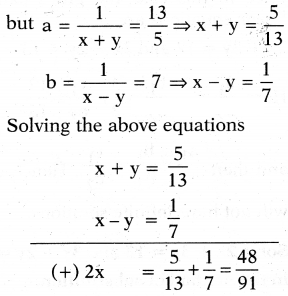
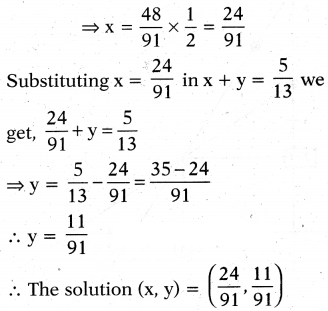
Question 24.
Cost of Mathematics textbook is Rs. 10 less than twice of cost of English text book. Write this in linear equation.

Solution:
Let the cost of English textbook = Rs. x
Twice of it = 2x Rs. 10 less to above = 2x - 10
Then cost of Mathematics textbook y = 2x - 10 is the required linear , equation.

Question 2.
Solve the pair 2x + 3y = 12 and
3x + 2y = 13 in elimination method.

Solution:
2x + 3y = 12 ....(1)
3x + 2y = 13 ..... (2)
Multiply the equation (1) with 3 on both sides, and the equation (2) on both sides.
We get
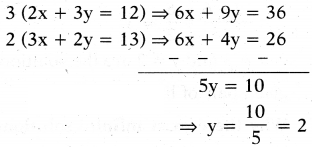2x + 3y = 12
⇒ 2x + 3(2) = 12
⇒ 2x + 6 = 12
⇒ 2x + 12 - 6 = 6
then x = 6/2 = 3
∴(2x + 3y = 12)
∴ x = 3 and y = 2 are the solution .

Question 25.
Solve the linear equations 2x + 3y = 12 and 3x + 2y = 13 by graph method.

Solution:
A linear equation can be expressed by a straight line on a graph.
The intersecting point of two straight lines is the solution of linear equation represented by them.
Now let us find the points on 2x + 3y = 12

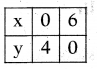
So the line represented by the equa¬tion 2x + 3y = 12 passes through the points (0, 4) and (6, 0).
Similarly 3x + 2y = 13 passes through the points (1, 5) and (3, 2)

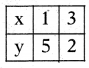
Now, see the graph
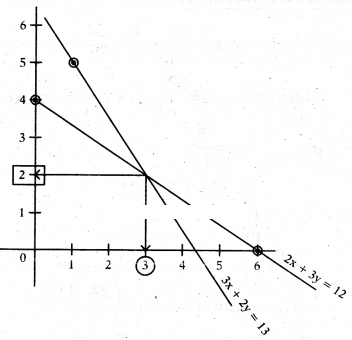So x = 3, and y = 2 is the solution of above system.

Question 26.
Say whether the solution for 2x + 3y = 12 and 3x + 2y = 13 is exist or not basing on the coefficients.

Solution:
The two linear equations a₁x + b₁y + C₁ = 0 and a₂x + b₂y + c₂ = 0 are consistent then their solution exists if and only if
a1/a2≠b1/b2
In the given two linear equations
2x + 3y = 12 and 3x + 2y = 13
a1/a2 = 2/3 ≠ 3/2 = b1/b2
Hence they are consistent and their solution exists.

Question 27.
Check whether the number of solutions of 2x + 3y = 12 and 3x + 2y = 13 are Infinity or not. Give reasons.

Solution:
The number of solutions to the pair of
linear equationsa₁x + b₁y + c₁ = 0
a₂x + b₂y + c₂ = 0 are infinity if and only if a1/a2 = b1/b2 = c1/c2
Here in this case the given pair of linear equations are
2x + 3y = 12 and 3x + 2y = 13
Here a1/a2 = 2/3, b1/b2 = 3/2,c1/c2 = 12/13
and then a1/a2 ≠ b1/b2 ≠ c1/c2
Hence they will not have infinite solutions.

Question 28.
Solve 2x + 3y = 12 and 3x + 2y = 13 in the method of substitution.

Solution:
The given equations are
2x + 3y - 12 ...... (1)
3x + 2y = 13 ...... (2)
∴ 2x = 12 - 3y [?From (1)]
x = 12-3y/2 ..... (3)
Substitute this value of x in given equa¬tion (2) we get
3 (12-3y/2) + 2y = 13
36-9y+4y/2 = 13
⇒ 36 - 5y = 13 x2 = 26
⇒ -5y = 26 -36 = - 10
∴ 5y = 10 and y = 1/5 = 2
Then from equation (3)
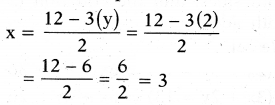∴ x = 3 and y = 2 are the solution for given pair of linear equations.

Question 29.
Why there exist infinite solutions to the straight line 2x + 3y = 12 ?

Solution:
2x + 3y = 12 can be represented by a straight line on x-y coordinate system.
Now the points lie on this straight line are infinite. All the points on the line satisfy the condition 2x + 3y = 16. Hence all
Such points are solutions to this straight line. Hence they are infinite.
For example
2x + 3y = 12