2nd Lesson Polynomials Class 10 Important Questions with Solutions
10th Class Maths Polynomials 1 Mark Important Questions
Question 1.
State the remainder theorem.
Solution:
Let p(x) be any polynomial of degree greater than or equal to one and let ‘a’ be any real number. If p(x) is divided by the linear polynomial x - a, then the remainder is p(a). That is
p(x) = (x - a).q(x) + p(a)
Question 2.
If α and β are the roots of p(x) = ax2 + bx + c, then find sum of the roots and product of the roots.
Solution:
Given polynomial p(x) = ax2 + bx + c
If α, β are roots then,
sum of roots (a + β) = -coefficient of x /coefficient of x2 = -b/a
product of roots
α.β = constant term coefficient of x2 = c/a
Question 3.
Find the roots of polynomial x2 - 16.
Solution:
x2 - 16 = 0
x2 = 16
x = ±4
Therefore roots are + 4 and - 4.
Question 4.
If f(x) = 2x3 + 5x2 + 6x + 9, find f(-1).
olution:
Put x = -1 in f(x) = 2x3 + 5x2 + 6x + 9
then f(-1) = 2(-1)3 + 5(-1)2 + 6 (-1) + 9
= 2(-1) + 5(1) -6 + 9
= - 2 + 5 - 6 + 9
= 6
∴ f(-1) = 6
Question 5.
Consider cubic polynomial x3 + 2x2 + 3x + 4. What is the sum of all roots ?
Solution:
Given p(x) = x3 + 2x2 + 3x + 4
Sum.of all roots α + β + γ = -b/a
= - coefficient of x2/coefficient of x3 = -2/1 = -2
Question 6.
If x = 2 is root of f(x) = x2 - x + k, then find k.
Solution:
Put x = 2 in f(x) = x2 - x + k
f(2) = (2)2 - (2) + k = 0
⇒ 4 - 2 + k = 0
⇒ 2 + k = 0
∴ k = -2
Question 7.
If p(x) = x2 + 5x + 6, then p(-2) is .....
Solution:
p(x) = x2 + 5x + 6
p(-2) = (-2)2 + 5 (-2) + 6
= 4 - 10 + 6 = 0
Question 8.
Write a quadratic polynomial whose sum and product of zeroes are 2 and -1 respectively.
Solution:
x2 - (α + β) x + αβ
α + β = 2 and ap = -1
= x2 - (2) = x - 1
= x2 - 2x - 1
Question 9.
What are the zeroes of the polynomial x2 - 3x - m(m + 3) ?
Solution:
x2 - 3x - m (m + 3)
Adding and subtracting mx
⇒ x2 - mx - 3x + mx - m(m + 3)
Let x(x - m - 3) + m(x - m - 3) = 0
⇒ (x - m - 3) (x + m) = 0
⇒ x - m - 3 = 0 (or)x + m = 0
∴ x = m + 3 or x = -m
Question 10.
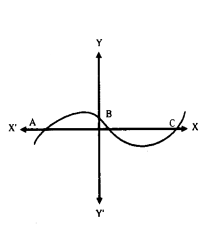
The graph of a polynomial p(x) cuts the X-axis at 3 points and touches it at 2 other points. Find the number of ze-roes of p(x).
Solution:
No. of zeroes = 3.
Example :
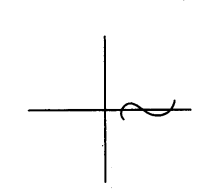
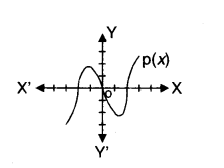
Question 11.
In the figure, the graph of a polynomial p(x) is shown. Find the number of zeroes of p(x).
Solution:
3
Question 12.
Write a quadratic polynomial, the product and sum of whose zeroes are 5 and 8 respectively.
Solution:
k(x2 - (α + β) x + αβ)
= k(x2 - 5x + 8)
Question 13.
If α, β are the zeroes of the quadratic polynomial p(x) = x2 - (k + 6)x + 2(2k - 1), then the value of k, if α + β = αβ is .......
A) -7
B) 7
C) -3
D) 3
Solution:
B) 7
p(x) = x2 - (k + 6) x + 2 (2k - 1)
a = 1, b = -(k + 6), c = 2(2k - 1)
α + β = 1/2 αβ (Given)
-b/a = c/2a
(ax2+ bx + c, a ≠ b, c ≠ 0)
-b = c2a
-2ab = c
-2 (1) (-(k + 6)) = 2(2k - 1)
2k + 12 = 4k - 2
12 + 2 = 4k - 2k
14 = 2k
∴ k = 14/2 = 7
Question 14.
Find the zeroes of a quadratic polynomial x2 - 5x + 6.
Solution:
x2 - 5x + 6 = 0
x2 - 2x - 3x + 6 = 0
x(x - 2) - 3(x - 2) = 0
(x - 3) (x - 2) = 0
x - 3 = 0 (or) x - 2 = 0
x = 3 or x = 2
Question 15.
If α and β are the zeroes of the polynomial x2 - 1, then find the value of (α + β).
Solution:
x2 - 1
a = 1, b = 0, c = -1
α + β = -b/a = -0/1 = 0
Question 16.
If one zero of the quadratic polynomial x2 + 3x + k is 2, then find the value of k.
Solution:
p(x) = x2 + 3x + k
P(2) = 0
⇒ (2)2 + 3(2) + k = 0
⇒ 4 + 6 + k = 0
⇒ k = -10
Question 17.
If - 1 is a zero of the polynomial p(x) = x2 - 7x - 8 then find the other zero.
Solution:
p(x) = x2 - 7x - 8.
x2 - 7x - 8 = 0
Let a, b are two zeroes.
a = -1, a + b = - (-7)/1
a + b = 7
- 1 + b = 7
∴ b = 8.
Question 18.
Write a quadratic polynomial sum of whose zeroes is 2 and product is -8.
Solution:
α + β = 2 αβ = -8
Quadratic polynomial
p(x) = k[x2 - (α + β)x + αβ
= k[x2 - 2x - 8]
k = 1 ⇒ p(x) = x2 - 2x - 8
Question 19.
What is the sum of the zeroes of the polynomial 2x2 - 8x + 6 ?
Solution:
α + β = -b/a = -(-8)/2 = 8/2 = 4.
Question 20.
The following figure shows the graph of y = p(x), where p(x) is a polynomial in variable x, find the number of zeroes of the polynomial p(x).
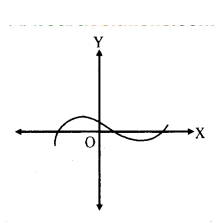
Solution:
The curve touches X-axis at 3 points then the zeroes are 3.
Question 21.
Graph of a polynomial p(x) is given in the figure. What is the number of zeroes of p(x) ?
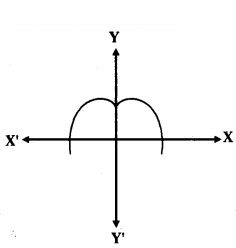
Solution:
The curve touches X-axis at 2 points, then the number of zeroes are 2.
Question 22.
Assertion (A) : Polynomial x2 + 4x has two real zeroes.
Reason (R) : Zeroes of the polynomial x2 + ax, a ≠ 0 are 0 and a.
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Solution:
C) Assertion (A) is true but reason (R) is false.
Question 23.
If α, β, γ are the zeroes of the polynomial px3 + qx2 + rx + s then, which of the following matching is correct ?
A) α + β + γ
B) αβ + βγ + αγ
C) αβγ
i) - s/p
ii) - q/p
iii) b/a
a) A(i), B(ii), C(iii)
b) A(ii), B(iii), C(i)
c) A(iii), B(i), C(ii)
d) A(ii), B(i), C(iii)
Answer:
b) A(ii), B(iii), C(i)
Question 24.
What is the zero of the polynomial 3x - 2 ?
Solution:
f(x) = 3x - 2; f(x) = 0
3x - 2 = 0 ⇒ 3x = 2 ⇒ x = 1/2
Question 25.
Write the polynomial in variable ∴x∵ whose zero is k/a .
x - (- k/a) = 0 ⇒ x + k/a = 0
⇒ ax + k = 0
∴ ax + k = 0 is a polynomial with degree
∴1∵ in variable ∴x∵ whose zero is - k/a.
Question 26.
Which of the following is a polynomial?
A) 1/x+1
B) 6√x + 8
C) x-3 + 2x
D) √5m + 6
Answer:
D) √5m + 6
Question 27.
If α, β, γ are zeroes of polynomial 4x3 - 2x2 + 7, match the following.
a) γ + β + α
b) αβ + βγ + γα
c) αβγ
i) - 7/4
ii) 1/2
iii) 0
A) a - i, b - ii, c - iii
B) a - iii, b - i, c - ii
C) a - ii, b - iii, c - i
D) a - ii, b - i, c - iii
Answer:
C) a - ii, b - iii, c - i
Question 28.
Find the sum of the zeroes of a cubic polynomial 2x3 - 5x + 7.
Answer:
0 (zero).
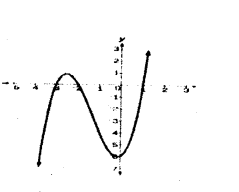
Question 29.
Find the number of zeroes of the polynomial p(x), whose graph is given.
Answer:
3
Question 30.
Choose the correct answer satisfying the following statements.
Statement (A) : Number of maximum zeroes of a cubic polynomial is 3.
Statement (B) : Zero of a linear polynomial x - 2 is - 2.
i) Both (A) and (B) are true.
ii) (A) is true, (B) is false.
iii) (A) is false, (B) is true.
iv) Both (A) and (B) are false.
Answer:
ii) (A) is true, (B) is false.
Question 31.
Number of zeroes of a cubic polynomial ....... .
Answer:
3.
Question 32.
Sum of the zeroes of polynomial x2 - 1 is ....... .
Answer:
0 [∵ - 1 + 1 = 0]
Question 33.
Degree of the polynomial p(x), whose graph is given below is ....... .
Answer:
Cubic polynomial
Question 34.
Choose the correct answer by observ-ing the following statements.
Statement I: The number of zeroes of the quadratic polynomial is at most 2.
Statement II: If α, β are zeroes of the quadratic polynomial ax2 + bx + c (a ≠ 0), then α + β = c/a
A) Both statements are true.
B) Statement I is true ; statement II is false.
C) Statement I is false ; statement II is true.
D) Both statements are false.
Answer:
B) Statement I is true ; statement II is false.
Question 35.
Choose the correct answer satisfying the following statements :
Statement (P) : The degree of the quadratic polynomial is 2.
Statement (Q) : Maximum no.of zeroes of a quadratic polynomial is 2.
A) Both (P) and (Q) are true
B) (P) is true, (Q) is false
C) (P) is false, (Q) is true
D) Both (P) and (Q) are false
Answer:
A) Both (P) and (Q) are true
10th Class Maths Polynomials 2 Marks Important Questions
Question 1.
If ax3 + bx2 + cx + d is a cubic polynomial whose roots are α, β, γ then write
i) α + β + γ
ii) α.β + β.γ + γ.a
iii) α.β.γ
Solution:
Given p(x) = ax3 + bx2 + cx + d
If α, β, γ are roots of p(x).
(i) Sum of roots
α + β + γ = - coefficient of x2 /coefficient of x3
α + β + γ = -b/a
Sum of roots taking two at α time
ii) α.β + β.γ + γ.a = coefficient of x/coefficient of x3
α.β + β.γ + γ.a = -b/a
(iii) Product of the roots iii) α.β.γ
= -constant/coefficient of x3 = -d/a
Question 2.
Find the quadratic polynomial if sum and product of roots are 3/2 and 5/2 respectively.
Solution:
Given sum of roots α + β = 3/2 = -b/a and product of roots α.β = 5/2 = c/a
then a = 2, b = -3 and c = 5
Quadratic polynomial is ax2 + bx + c That is quadratic polynomial is 2x2 - 3x + 5.
Question 3.
Check whether the first polynomial is the factor of second polynomial or not: x - 3, x2 - 9.
Solution:
First polynomial = x - 3
Second polynomial = x2 - 9 = (x + 3)(x- 3)
(x - 3) can divide the (x + 3)(x - 3)
So, (x - 3) is a factor of (x + 3)(x - 3) or x2 - 9.
Question 4.
If x = 4/3 is a root of the polynomial f(x) = 6x3 - 11x2 + kx - 20, then find the value of k.
Solution:
Given f(x) = 6x3 - 11x2 + kx - 20
Put x = 4/3 in f(x)
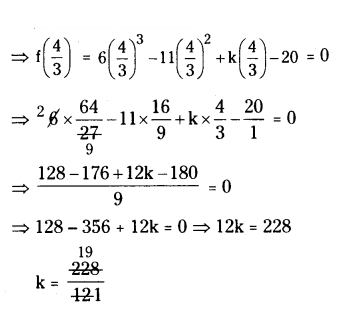
∴ k = 19
Question 5.
If α, β are zeroes of the quadratic polynomial ax2 + bx + c, then find the value of α2 - β2.
Solution:
We know, sum of the roots α + β = -b/a and product of roots α.β = c/a
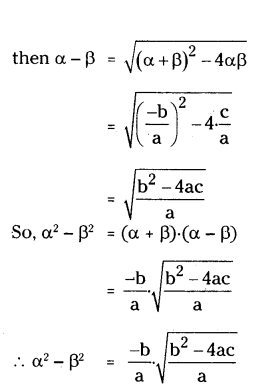
Question 6.
A teacher asked 10 of his students to write a polynomial in one variable on a paper and then to handover the paper. The following were the answer given by the students.
2x + 3, 3x
2 + 7x - 2, 4x
3 + 3x
2 + 2, x
3 +
√3 x + 7, 7x + √7, 5x
3 - 7x + 2, 2x
2 + 3 - 1/x
Answer the following questions.
i) How many of the above ten are not polynomials ?
H) How many of the above ten, are quadratic polynomials ?
Solution:
i) 2(2x2 + 3 - 5/x, x + 1/x)
ii) 1 (3x2 + 7x + 2)
Question 7.
A teacher told 10 students to write a polynomial on the black board.
Students wrote:
1) x2 + 2
2) 2x + 3
3) x3 + x2 + 1
4) x3 + 2x2 + 1
5) x2 - 2x + 1
6) x - 3
7) x4 + x2 + 1
8) x2 + 2x + 1
9) 2x3 - x2
10) x4 - 1
Answer the following questions.
(i) How many students wrote cubic polynomial ?
(ii) Divide the polynomial (x2 + 2x + 1) by x + 1.
Solution:
i) 3
ii) x2+2x+1/x+1 = x2+x+x+1/x+1
= x(x+1)+1(x+1)/x+1
= (x+1)2/x+1 = x + 1
Question 8.
Find the quadratic polynomial whose zeroes are 6 and -3.
Solution:
Let α = 6, β = -3
The Quadratic polynomial is
k(x2 - (α + β)x + αβ)
k(x2 - (6 - 3)x + 6 × (-3))
k(x2 - 3x- 18)
Let k = 1 l(x2 - 3x - 18)
∴ The required polynomial = x2 - 3x - 18.
Question 9.
Find the zeroes of the polynomial x2 + 4x - 12.
Solution:
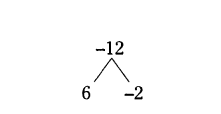
Let x2 + 4x- 12 = 0
x2 + 6x - 2x - 12 = 0
x[x + 6] - 2[x + 6] = 0
(x - 2) (x + 6) = 0
x - 2 = 0 (or) x + 6 = 0
x = 2 (or) x = -6.
Question 10.
If one zero of the polynomial p(x) = 6x2 + 37x - (k - 2) is reciprocal of the other, then find the value of k.
Solution:
Let p(x) = 6x2 + 37x - (k - 2)
a = 6, b = 37, c = -k + 2 = 2 - k.
Let α and 1/α are the zeroes of p(x) as a the zeroes are reciprocal to each other.
α + 1/α -b/a = -37/6; α(1/α) = c/a
1 = 2-k/6
∴ 2 - k = 6
2 - 6 = k
-4 = k
k = -4
Question 11.
Find the quotient x5+x4+x3+x2/x3+x2+x+1 when x ≠ 1.
Solution:
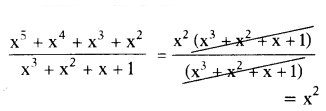 So the quotient is [x2]
So the quotient is [x2]
Question 12.
We can write a trinomial having degree 7th Justify the given statement by giving one example.
Solution:
Since the required is a trinomial, it should have 3 terms. As its degree is 7 the highest exponent (power) of the variable is 7. So the required will be
1) x7 - x6 + x5 (or) x7 - x + 10 (or) x7 - x5 - x (or) x7 + 5x6 + 6x5 or ..
Question 13.
For what value of k, - 4 is a zero of the polynomial x2 - x - (2k + 2).
Solution:
Given polynomial = f(x) = x2 - x - (2k + 2)
- 4 is a zero of f(x), so x = - 4.
Put x = - 4 then f(x) becomes zero
f(-4) = (-4)2 - (- 4) - (2k + 2) = 0
⇒ 16 + 4 - 2k - 2 = 0
⇒ 18 - 2k = 0
2k = 18 ⇒ k = 18/2 = 9
∴ The value of ∵k∵ is 9
Question 14.
Write an example for a quadratic polynomial which has no zeroes.
Solution:
A quadratic polynomial is in the form of ax2 + bx + c. As this has no zeroes, its discriminant will not be a real number.
So b2 - 4ac < 0
So we can choose certain a, b, c values where b2 - 4ac < 0
For examples a = 1 b = 4 and c = 9
So ax2 + bx + c = 0
⇒ x2 + 4x + 9 = 0 will not have zeroes,
Question 15.
If p(x) = x3 - 3x2 + 2x - 3 is a polynomial, then find the value of p(1).
Solution:
p(x) = x3 - 3x2 + 2x - 3
p(1) = (1)3 - 2(1)2 + 2(1) - 3
= 1 - 3 + 2 - 3 = 3 - 6 = -3
Question 16.
Srikar says that the order of the polynomial (x2 - 5) (x3 + 1) is 6. Do you agree with him ? How ?
Solution:
(x2 - 5)(x3 + 1) = x5 + x2 - 5x3 - 5
As its degree is 3 I do not agree with Srikar.
Question 17.
Find the zeroes of the polynomial
p(x) = x
2 - 4.
Solution:
p(x) = x2 - 4
x2 - 4 = 0
x2 = 4
∴ x = √4 = ± 2 .
Question 18.
Verify the relation between zeroes and coefficients of the Quadratic polynomial x2 - 4.
Solution:
p(x) = x2 - 4
= (x +2) (x - 2)
So zeroes are 2 and - 2
Sum of zeroes = 2 + (- 2) = 0
Product of zeroes = 2 (- 2) = - 4.
p(x) - x2 - 4
a = 1, b = 0, c = - 4
Sum of zeroes = -b/a = -0/1 = 0
Product of zeroes c/a = -4/1 = - 4.
Question 19.
If P(x) = x4 + 1, then find P(2) - P(- 2).
Solution:
P(x) = x4 + 1
P(2) = (2)4 + 1 = 16 + 1 = 17
P(-2) = (-2)4 + 1 = 16 + 1 = 17
P(2) - P(-2) = 17 - 17 = 0
Question 20.
Whether 1/2 and 1 are zeroes of the polynomial p(x) = 2x2 - 3x + 1 or not ? Justify.
Solution:
p(x) = 2x2 - 3x + 1
p(1/2)= 2(1/2)2 - 3(1/2) + 1
= 1/2 - 3/2 + 1 = 0
p(1) - 2(1)2 - 3(1) + 1 = 2 - 3 + 1 = 0
∴ 1/2 and 1 are zeroes of the polynomial p(x).
Question 21.
-3, 0 and 2 are the zeroes of the polynomial p(x) = x3 + (a - 1)x2 + bx + c, find a and c.
Solution:
Given solution compare with
ax3 + bx2 + cx + d
Given equation p(x) = x3 (a - 1) x2 + bx + c.
Given roots -3, 0, 2
Sum of the roots ⇒ α + β + γ = -b/a
- 3 + 0 + 2 = -(a-1)/1
-1 = -a + 1 ⇒ -1 -1 = -a
∴ a = 2
Product of the roots αβγ = -d/a
(-3) (0) (2) = -c/1 ⇒ c = 0
∴ a = 2 and c = 0
Question 22.
Write any two linear polynomials having one term and three terms.
Solution:
Linear polynomial one term = 2x.
Linear polynomial three terms = x + y + z
Question 23.
If p(x) = x2 + 3x + 4, then find the values of p(0) and p(1).
Solution:
p(x) = x2 + 3x + 4
p(0) = (0)2 + 3(0) + 4 = 0 + 0 + 4 = 4
∴ p(0) = 4
p(1) = (1)2 + 3(1) + 4 = 1 + 3 + 4 = 8
∴ p(1) = 8
Question 24.
If p(x) = x2 - 5x - 6; find the value of p(3).
Solution:
p(x) = x2 - 5x - 6 (given)
p(3) = 32 - 5(3) - 6
= 9 - 15 - 6 = 9 - 21 = -12
So p(3) = - 12.
Question 25.
Write two more polynomials and cre-ate two questions for each of them.
Solution:
i) x2 - 5x + 6 (polynomial (i))
Questions :
1) What is the order of the polynomial ?
2) What are the zeroes of the polynomial?
ii) x2 - (4x) (polynomial (ii))
Questions :
1) How many zeroes are there to this polynomial ?
2) Do this polynomial has ∴O∵ as its zero value ?
Question 26.
If p(y) = y3 - 1, then verify that 1,-1 are the zeroes of p(y) or not.
Solution:
p(y) = y3 - 1
p(1) = 13 - 1 = 1 - 1 = 0
∴ ∴1∵ is the zero of p(y).
p(- 1) = (-1)3 - 1 = - 1 - 1 = -2
∴ ∴-1∵ is not zero of p(y).
Question 27.
For what value of k, is 3 a zero of the polynomial 2x2 + x + k.
Solution:
Since 3 is a zero of the polynomial
p(x) = 2x2 + x + k, p(3) = 0
∴ p(3) - 2(3)2 + 3 + k = 0
⇒ 21 + k = 0 ⇒ k = -21
Question 28.
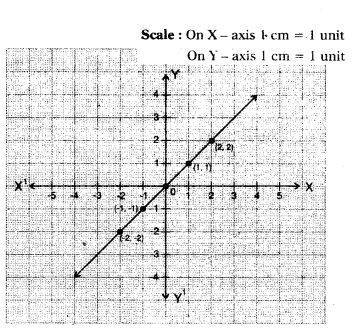
Draw a rough graph of x - y = 0.
Solution:
| x |
y |
(x, y) |
| 0 |
0 |
(0, 0) |
| 1 |
1 |
(1, 1) |
| -1 |
-1 |
(-1, -1) |
| -2 |
-2 |
(-2, -2) |
| 2 |
2 |
(2, 2) |
Question 29.
Observe the following graph and answer the following questions.
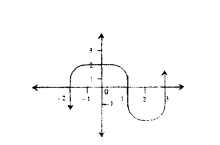
i) Which type of polynomial represented by the curve?
ii) What are the zeros of given polynomial ?
Solution:
i) The given curve crosses X-axis at 3 points. Hence the curve represents a cubic polynomial.
ii) The given curve crosses at the points (- 2, 0), (1, 0) and (3, 0). Hence the zeroes ofgiven polynomial are (-2, 1, 3).
10th Class Maths Polynomials 4 Marks Important Questions
Question 1.
Find the zeroes of the quadratic polynomial x2 + 7x + 12 and verify the relation between the zeroes and its coefficients.
Solution:
Given p(x) = x2 + 7x + 12
= x2 + 4x + 3x + 12
= x(x + 4) + 3(x + 4)
p(x) = (x + 4)(x + 3)
x + 4 = 0
x = -4
x + 3 = 0
x = -3
Therefore, x = -4 (or) -3
Zeroes of p(x) = x2 = - 4 + 7x + 12 are - 4 and -3.
Let α = - 4, β = -3
Sum of zeroes = α + β
= - 4 + (-3) = - 4 - 3
= -7

Question 2.
Find the zeroes of the polynomial f(y) = 4y2 + 8y and verify the relationship between the zeroes and its coefficients.
Solution:
Given f(y) = 4y2 + 8y = 4y(y + 2)
4y = 0
y = 0
y + 2 = 0
y = -2
Therefore, zeroes of f(y) = 4y2 + 8y are y = 0 (or) -2.
Let roots are α = 0 and β = -2
then, sum of roots = α + β = 0 + (-2) = -2
Sum of roots = coefficient of -y coefficient of y/2 = -8/4 = -2
Product of roots = α.β = 0 × (-2) = 0
Product of roots = Constant term coefficient of x/2 = 0/4 = 0
Question 3.
If α and β are the zeroes of the qua-dratic polynomial f(x) = x2 - x - 4, find the value of 1/α + 1/β - αβ.
Solution:
Given, f(x) = x2 - x - 4
α, β are the roots of the f(x).
Product of roots = α + β = -(-1/1) = 1/1 = 1

Question 4.
Divide the polynomial f(x) = 3x2 - x3 - 3x + 5 by the polynomial g(x) = x - 1 - x2 and verify the division algorithm.
Solution:
Given, f(x) = 3x2 - x3 - 3x + 5
and g(x) = x - 1 - x2
write in the standard form
f(x) = - x3 + 3x2 - 3x + 5 and
g(x) = - x2 + x - 1
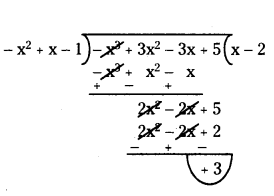
q(x) = x - 2, r(x) = 3
Verification:
Dividend = quotient × divisor + remainder
f(x) = q(x) × g(x) + r(x)
= (x - 2) (- x2 + x - 1) + 3
= - x3 + x2 - x + 2x2 - 2x + 2 + 3
f(x) = - x3 + 3x2 - 3x + 5
Hence verified.
Question 5.
Find a cubic polynomial with sum and the sum of the product of its zeroes taken two at a time and the product of its zeroes as 2, -7, -14 respectively.
Solution:
Let the cubic polynomial p(x) = ax3 + bx2 + cx + d and its zeroes are α, β and
γ.
α + β + γ = 2
αβ + βγ + αγ = -7 and αβγ = -14
α + β + γ = 2 = -(-2)/1 = -b/a
αβ + βγ + aγ = -7 = -7/1 = c/a
αβγ = -14 = -14/1 = -d/a
∴ a = 1, b = -2, c = -7 and d = 14
1x3 + (-2)x2 + (-7)x + 14
x3 - 2x2 - 7x + 14
So, the cubic polynomial which satisfies the given condition is x3 - 2x2 - 7x + 14.
Question 6.
If the zeroes of the polynomial x3 - 3x2 + x + 1 are a - b, a, a + b, find a and b.
Solution:
Given polynomial p(x) = x3 - 3x2 + x + 1
and a - b, a and a + b are zeroes of polynomial p(x).
So, sum of the zeroes
= a - b + a + a + b = -(-3)/1
3a = 3
∴ a = 3/3 = 1
sum of the product of its zeroes taken two at a time.
⇒ a(a - b) + a(a + b) + (a + b) (a - b) = 1/1 = 1
⇒ a2 - ab + a2 + ab + a2 - b2 = 1
⇒ 3a2 - b2 = 1
⇒ 3(1)2 - b2 = 1
⇒ -b2 = 1 - 3
⇒ -b2 = - 2
⇒ b = ±√2
∴ a = 1 and b = ± √2
Question 7.
Find the zeroes of the polynomial 6x2 - 3 - 7x.
Solution:
Given f(x) = 6x2 - 7x - 3
= 6x2 - 9x + 2x - 3
= 3x (2x - 3) + 1 (2x - 3)
= (3x + 1) (2x - 3)
then f(x) = (3x + 1) (2x - 3) = 0
⇒ 3x + 1 = 0 (or) 2x - 3 = 0
∴ x = -1/3 (or) 3/2
Therefore, zeroes of f(x) = 6x2 - 7x - 3
are α = -1/3 and β = 3/2.
Question 8.
If α, β are the zeroes of the polynomial f(x) = 2x2 + 5x + k satisfying the relation α2 + β2 + α.β = 21/4, then find the value of k.
Solution:
Given α, β are the zeroes of f(x) = 2x2 + 5x + k
a = 2, b = 5, c = k
Sum of zeroes = α + β = -b/a = -5/2
Product of zeroes = α.β = c/a = k/2
Given α2 + β2 + α.β = 21/4
(α2 + β2 + 2α.β) - α.β = 21/4
(α + β)2 - α.β = 21/4
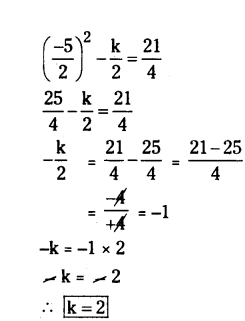
Question 9.
In α and β are the zeroes of the polynomial f(x) = ax2 + bx + c, then find
i) α2 + β2
ii) α/β + β/α
Solution:
Given α and β are zeroes of f(x) = ax2 + bx + c, then sum of zeroes α + β = -b/a and product of roots α.β = c/a
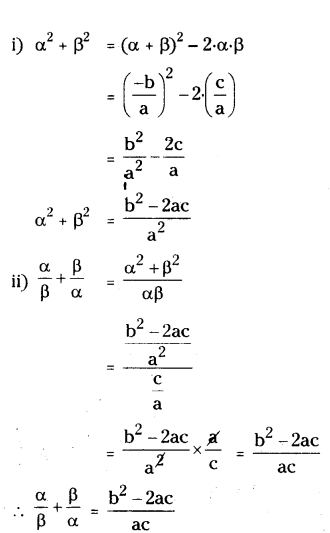
Question 10.
If sum of the squares of zeroes of f(x) = x2 - 8x + k is 40, find k.
Solution:
Let α and β are the zeroes of f(x) = x2 - 8x + k
Then sum of zeroes α + β = -b/a = -(-8)/1 = 8
Product of zeroes α.β = k/1 = k
Given α2 + β2 = 40
(α + β)2 - 2αβ = 40
(8)2 - 2k = 40
-2k = 40 - 64 = -24
k = 24/2 = 12
∴ k = 12
Question 11.
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively :
i) 1/4, -1
ii) 0, √5
Solution:
The quadratic polynomial when the sum and product of zeroes are given by f(x) = x2 - (Sum of zeroes)x + (Product of zeroes)
i) Sum of zeroes = 1/4 and product of zeroes = -1
f(x) = k[x2 - (1/4) x + (-1)]
= k(4x2-x-4/4)
∴ f(x) = k 1/4 (4x2 - x - 4)
= k/4 (4x2 - x - 4)
When k = 1
The Quadratic polynomial
f(x) = 1/4 (4x2 - x - 4)
ii) Sum of zeroes = 0, and product of zeroes = √5
f(x) = k[x2 - (0)x + √5]
= k(x2 + √5)
∴ f(x) = k(x2 + √5)
When k = 1
The quadratic polynomial
f(x) = x2 + √5
Question 12.
If α, β are zeroes of the quadratic polynomial x2 - 5x + 6 form another quadratic polynomial whose zeroes are 1/α, 1/β.
Solution:
x2 - 5x + 6
a = 1, b = -5, c = 6.
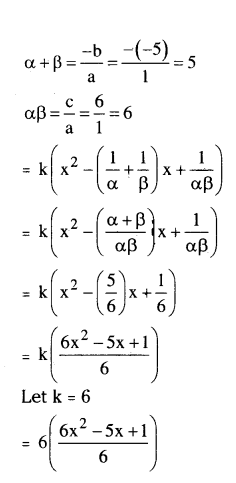 6x2 - 5x + 6
6x2 - 5x + 6
∴ p(x) = 6x2 - 5x + 1 is the required polynomial.
Question 13.
Find the zeroes of the quadratic polynomial 4s2 - 4s + 1 and verify the relationship between the zeroes and the coefficients.
Solution:
Let p(s) = 4s2 - 4s + 1
⇒ (2s)2 - 2 . 2s . 1 + 12 = 0
⇒ (2s - 1)2 = 0
⇒ 2s - 1 = 0
⇒ 2s = 1
∴ s = 1/2
∴ The zeroes are 1/2 and 1/2.
Verification:
Sum of zeroes = 1/2 + 1/2 = 1/2 = 1
Product of zeroes = 1/2 × 1/2 = 1/4.
Comparing 4s2 - 4s + 1 with ax2 + bx + c, a ≠ 0
a = 4, b = -4, c = 1
α + β = -b/a = -(-4)/4 = 4/4 = 1
αβ = c/a = 1/4.
Hence verified.
Question 14.
Find the zeroes of the quadratic polynomial 6x2 - 3 - 7x and verify the relationship between the zeroes and the coefficients.
Solution:
p(x) = 6x2 - 3 - 7x
p(x) = 6x2 - 7x - 3
6x2 - 7x - 3 = 0
6x2 - 9x + 2x - 3 = 0
3x (2x - 3) + 1(2x- 3) = 0
(2x - 3) (3x + 1) = 0
2x - 3 = 0 (or) 3x + 1 = 0
2x = 3 (or) 3x = -1
x = 3/2 (or) x = -1/3
Verification :
Sum of zeroes = 3/2 - 1/3 = 9-2/6 = 7/6
Product of zeroes = 3/2 × -1/2 = -1/2
On comparing with ax2 + bx + c, we get
a = 6, b = -7, c = -3
α + β = -b/a = -(-7)/6 = 7/6
αβ = -3/6 = -1/2
Hence verified.
Question 15.
If we multiply or divide both sides of a linear equation by a non zero number, then the roots of linear equation will remain the same. Is it true ? If so justify with an example.
Solution:
Let linear equation be 2x + 8 = 11
Its solution is
2x = 11 - 8 ⇒ 2x = 3 So x = 3/2
Let the 2x + 8 = 11 linear equation is multiplied by 10 on both sides.
(2x + 8= 11)10 = 20 x + 80 = 110
⇒ 20x = 110 - 80 = 30
then x = 30/20 = 3/2
So its solution doesn∵t change.
So the given statement is true.
Question 16.
The length of a rectangle is 5 more than its breadth. So express its perimeter in the form of polynomial.
Solution:
Let the breadth of rectangle = x m and its length = x + 5 m.
So the perimeter = 2(l + b)
= 2 (x + 5 + x)
= 2 (2x + 5)
= 4x + 10 m
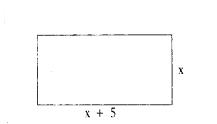
4x + 10 is the polynomial which represents the perimeter of above rectangle.
Question 17.
Show that 2 and - 1/3 are zeroes of the polynomial 3x2 - 5x - 2.
Solution:
p(x) = 3x2 - 5x - 2
p(2) = 3(2)2 - 5(2) - 2
= 12 - 10 - 2 = 12 - 12 = 0
p(-1/3) = 3(-1/3)2 - 5(-1/3) - 2
= 1/3 + 5/3 - 2 = 2 - 2 = 0
∴ 2 and - are zeros of p(x).
Question 18.
Which of √2 and 2 is a zero of the polynomial p(x) = x3 - 2x ? Why ?
Solution:
p(x) = x3 - 2x
P(√2) = (√2)3 - 2(√2) = 2√2 - 2√2 = 0
p(2) = (2)3 - 2(2) = 8 - 4 = 4.
Since p(32) = 0, 32 is a zero of the polynomial
Question 19.
If one of the zeroes of the cubic polynomial p(x) = ax3 + bx2 + cx + d is zero, then find the product of other two zeroes of p(x). (a ≠ 0)
Solution:
p(x) = ax3 + bx2 + cx + d
Let the zeroes of the polynomial be α, β and γ , given γ = 0.
αβ + βγ + γα = c/a
αβ = c/a [∵ γ = 0]
Question 20.
Find the quadratic polynomial, whose zeroes are 2/3 and 2.
Solution:
Let the quadratic polynomial be ax2 + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = 2/3 and β = 2. .
Sum of the zeores = α + β = 2/3 + 2 = 8/3
Product of the zeroes = αβ = 2/3 (2) = 4/3
∴ The quadratic polynomial ax2 + bx + c is
= [x2 - (α + β)x + αβ]
= [x2 - 8/3 x + 4/3
The quadratic polynomial will be 3x2 - 8x + 4.
Question 21.
Find the zeroes of the quadratic polynomial 5x2 - 4 - 8x and verify the relation between the zeroes and its coefficients.
Given polynomial is 5x
2 - 4 - 8x
= 5x
2 - 8x - 4
= 5x
2 - 10x + 2x - 4
= 5x(x - 2) + 2(x - 2) = (x - 2) (5x+ 2)
To find zeroes, (x - 2) (5x + 2) = 0
⇒ x - 2 = 0 or 5x + 2 = 0
⇒ x = 2 or x = - 2/5
Sum of the zeroes = 2 + (-2/5) = (8/5)
= -(-8)/5 = -Coefficient of x/Coefficient of x
2
Product of zeroes = 2(-2/5) = -4/5 = Constant/Coefficient of x
2
Question 22.
Write the quadratic polynomial, whose sum of zeroes is -3 and sum of the squares of zeroes is 17.
Solution:
The general form of quadratic polynomial having α, β as its zeroes is x2- (sum of zeroes)x + product of zeroes.
= x2 - (α + β) x + αβ,
here given (α + β) = -3 and (α2 + β2) = 17
∴ (α + β)2 = α2 + β2 + 2αβ
(-3)2 = 17 + 2αβ ⇒ 2αβ = 9 - 17 = -8
∴ αβ = - 8/2 = -4
∴ The required polynomial is x2 - (-3) x + (-4) = x2 + 3x - 4 is required quadratic polynomial.
Question 23.
If p and q are the zeroes of the polynomial 3x2 - 5x + 2, write the polynomial in ∴x∵ whose zeroes are 1/p and 1/q.
Solution:
It is given that, p and q are zeroes of polynomial 3x2 - 5x + 2.
Sum of zeroes = p + q = -(-5)/3 = 5/3 ..... (1)
Product of zeroes = pq = 2/3 ..... (2)
Now we have to find the polynomial
zeroes of which are 1/p and 1/q.
Sum of zeroes = 1/p + 1/q = p+q/pq
= 5/3/2/3 = 5/2
Product of zeroes = 1/p × 1/q = 1/pq
= 1/2/3 = 3/2
Now polynomial is x2 - (5/2)x + 3/2
= (2x2 - 5x + 3)/2
Hence required polynomial is 2x2 - 5x + 3.
Question 24.
Find the zeroes of the polynomial x2 + 7x + 10 and verify the relation between the co-efficients of the polynomial and the zeroes of the polynomial.
Solution:
Given polynomial p(x) = x2 + 7x + 10
x2 + 7x + 10 = 0
x2 + 5x + 2x + 10 = 0
x (x + 5) + 2 (x + 5) = 0
(x + 5) (x + 2) = 0
x + 5 = 0 (or) x + 2 = 0
.∵. x = -5 (or) x = -2
.∵. The zeroes of
x2 + 7x + 10 are -5, -2.
Let a = -5, b = -2 7
Sum of zeroes a + b = (-5) + (-2) = -7
= -7/1 = -x coefficient /x2coefficient
Product of zeroes ab = (-5) (-2)
= 10 = 10/1 = -x constant/ x2 coefficient
10th Class Maths Polynomials 8 Marks Important Questions
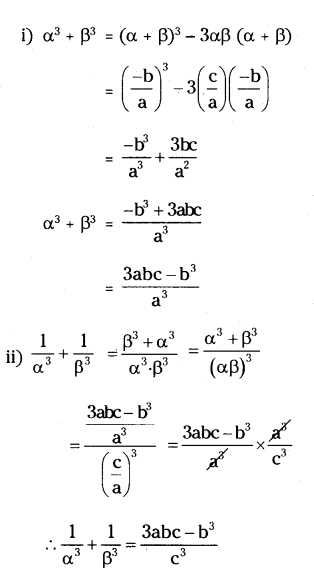
Question 1.
If α, β are the zeroes the quadratic polynomial p(x) = ax2 + bx + c, then find the value of
i) α3 + β3
ii) 1/α3+1/β3
iii) α2/β+β2/α
iv) α4 + β4
v) α2/β2+β2/α2.
Solution:
Given, p(x) = ax2 + bx + c
α and β are the zeroes of p(x).
Sum of roots = α + β = -b/a
Product of roots = α.β = c/a
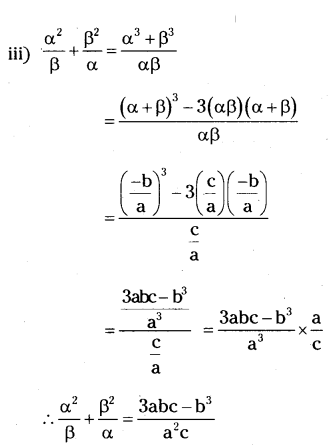
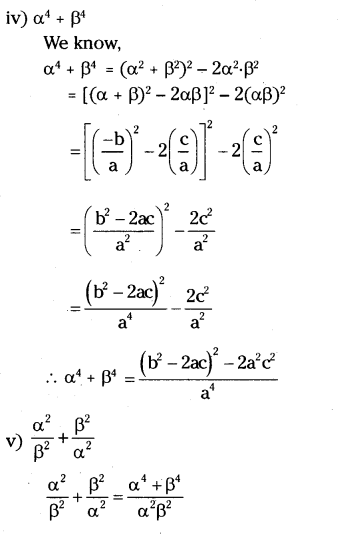
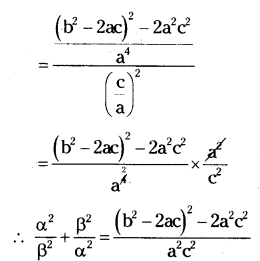
Question 2.
If α and β are the zeroes of the quadratic polynomial p(x) = x2 - x - 2, find a polynomial whose zeroes are 2α + 1 and 2β + 1.
Solution:
Given α and β are the zeroes of the polynomial p(x) = x2 - x - 2
Sum of the roots = α + β = (-1/1) = 1/1= 1
Product of roots = α.β = -2/1 = -2
Let A denoted the sum of zeroes of required polynomial
A = (2α + 1) + (2β + 1)
= 2α + 2β + 2
= 2 (α + β) + 2 (∵ α + β = 1)
∴ A = 2 (1) + 2 = 4
Let B denoted the product of zeroes of required polynomial
B = (2α + 1).(2β + 1)
= 4αβ + 2α + 2β + 1
= 4 (αβ) + 2 (α + β) + 1
= 4 (-2) + 2 (1) +1
∴ B = - 8 + 2 + 1 = -5
Polynomial is x2 - x (Sum of roots) + (Product of roots)
= x2 - Ax + B = x2 - 4x + (-5) = x2 - 4x - 5
∴ Required polynomial is x2 - 4x - 5.
Question 3.
Find the quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax2 + bx + c, a ≠ 0, c ≠ 0.
Solution:
Let α and β are the zeroes of polynomial f(x) = ax2 + bx + c
Then sum of roots α + β = -b/a
and product of roots α.β = c/a
Let P be the sum of roots and Q be the product of roots of a polynomial whose roots are 1/α and 1/β.
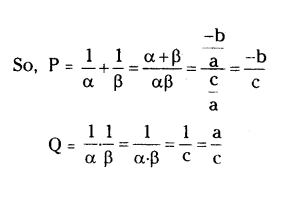
Question 4.
Divide the polynomial f(x) = x4 - 5x + 6, by the polynomial g(x) = 2 - x2 and verify the division algorithm.
Solution:
Given, f(x) = x4 - 5x + 6
and g(x) = 2 - x2
by writing the standard form we get, f(x) = x4 + 0x3 + 0x2 - 5x + 6
and g(x) = - x2 + 0x + 2
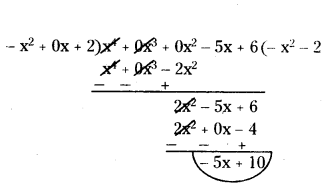
q(x) = - x
2 - 2 and r(x) = -5x + 10
Verification :
Dividend = quotient × divisor + remainder
f(x) = q(x) × g(x) + r(x)
= (- x2 - 2) (- x2 + 2) + (- 5x + 10)
= x4 + 2x2 - 2x2 - 4 - 5x + 10
f(x) = x4 - 5x + 6
Hence verified.
Question 5.
If two zeroes of the polynomial f(x) = x4 - 6x3 - 26x2 + 138x - 35 are 2 ± √3 find other zeroes.
Solution:
Given 2 + √3 and 2 - √3 are zeroes of the polynomial f(x) = x4 - 6x3 - 26x2 + 138x - 35
x = (2 + √3) and x = (2- √3)
x - (2 + √3) = 0 and x - (2 - √3) = 0
⇒ [x - (2 + √3)][x - (2 - √3)] = 0
⇒ (x - 2 - √3)(x - 2 + √3) = 0
⇒ (x - 2)2 - (√3)2 = 0
⇒ x2 - 4x + 4 - 3 = 0
∴ g(x) = x2 - 4x + 1
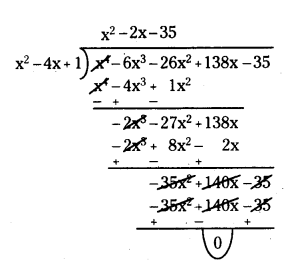
Now, q(x)= x2 - 2x - 35
= x2 - 7x + 5x - 35
= x (x - 7) + 5 (x - 7)
= (x - 7)(x + 5)
x - 7 = 0
x = 7
x + 5 = 0
x = -5
Therefore, other zeroes are 7 and -5.
Question 6.
What must be subtracted from 8x4 + 14x3 - 2x2 + 7x - 18. So that the result-ing polynomial is exactly divisible by 4x2 + 3x - 2.
Solution:
Given f(x) = 8x4 + 14x3 - 2x2 + 7x - 18
and g(x) = 4x2 + 3x - 2
2x2 + 2x - 1
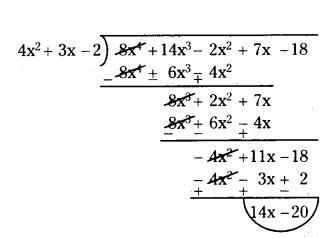
q(x) = 2x2 + 2x - 1 and r(x) = 14x - 20
If we subtract r(x) from f(x).
That is if we subtract 14x - 20 from f(x) = 8x4 + 14x3 - 2x2 + 7x - 18 it will be exactly divisible by g(x) = 4x2 + 3x - 2.
Question 7.
If the polynomial f(x) = x4 - 6x3 + 16x2 - 25x + 10 is divided by another polynomial x2 - 2x + k, the remainder comes out to be x + l, find k and l.
Solution:
Given, f(x) = x4 - 6x3 + 16x2 - 25x + 10 (dividend)
and g(x) = x2 - 2x + k (divisor)
r(x) = x + l (remainder) .
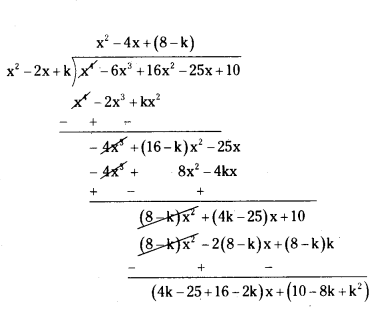
By comparing coefficients of the remainders
r(x) = 1x + l = (2k - 9)x + (k2 - 8k + 10)
2k - 9 = 1
2k = 9 + 1
k = 10/2 = 5
k2 - 8k + 10 = l
(5)2 - 8(5) + 10 = l
25 - 40 + 10 = l
-5 = l
∴ k = 5 and l = -5
Question 8.
Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :
i) p(x) = x3 - 3x2 + 5x - 3; g(x) = x2 - 2
Solution:
Given p(x) = x3 - 3x2 + 5x - 3 (Dividend)
g(x) = x2 - 2 (Divisor)
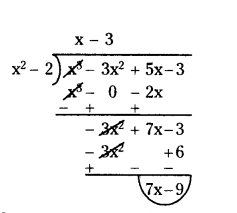
So, quotient is q(x) = x - 3
remainder is r(x) = 7x - 9
We know,
Dividend = Divisor × quotient + Remainder.
x3 - 3x2 + 5x - 3
ii) p(x) = x4 - 3x2 + 4x + 5
g(x) = x2 + 1 - x
Solution:
Given, p(x) = x4 - 3x2 + 4x + 5 (Dividend)
g(x) = x2 + 1 - x (Divisor)
Arrange the dividend and divisor in standard form.
p(x) = x4 - 3x2 + 4x + 5
g(x) = x2 + 1 - x
So, quotient is q(x) = x2 x - 3
remainder is r(x) = 8
We know,
Dividend = Divisor × Quotient + Remainder.
x4 - 3x2 + 4x + 5 = (x2 - x + 1) (x2 + x - 3) + 8.
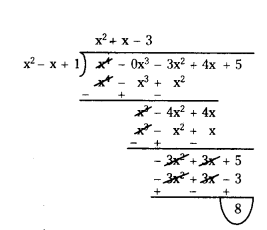
(iii) p(x) = x4 - 5x + 6; g(x)= 2 - x2
Solution:
Given, p(x) = x4 - 5x + 6 (Dividend)
g(x) = 2 - x2 (Divisor)
Arrange the dividend and divisor in decreasing order.
p(x) = x4 + ox3 + 0x2 - 5x + 6
g(x) = - x2 + 2
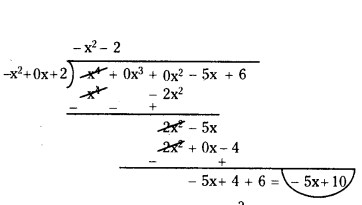
So, quotient is q(x) = - x2 - 2
remainder is r(x) = - 5x + 10
We know,
Dividend = Divisor × Quotient + Remainder.
x4 - 5x + 6 = (-x2 + 2) (- x2 - 2) + (-5x + 10).
Question 9.
Check whether the first polynomial is a factor of the second polynomial by dividing second polynomial by the first polynomial.
i) t
2 - 3, 2t
4 + 3t
3 - 2t
2 - 9t - 12
Solution:
Let p(t) = 2t4 + 3t3 - 2t2 - 9t - 12 (Dividend)
g(t) = t2 - 3 (Divisor)
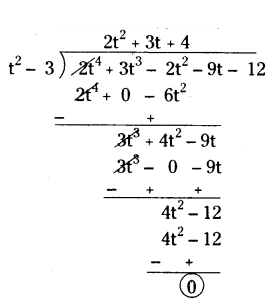
So, quotient q(t) = 2t2 + 3t + 4
remainder r(t) = 0
Therefore, g(t) = t2 - 3 is a factor of p(t) = 2t4 + 3t3 - 2t2 - 9t - 12
ii) x2 + 3x + 1, 3x4 + 5x3 - 7x2 + 2x + 2
Solution:
Let p(x) = 3x4 + 5x3 - 7x2 + 2x + 2 (Dividend)
g(x) = x2 + 3x + 1 (Divisor)
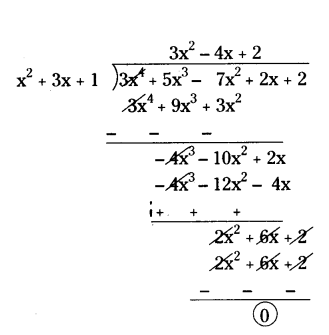
So, quotient q(x) = 3x2 - 4x + 2
remainder r(x) = 0
Therefore, g(x) = x2 + 3x + 1 is a factor of p(x) = 3x4 + 5x3 - 7x2 + 2x + 2
iii) x3 - 3x + 1, x5 - 4x3 + x2 + 3x + 1
Solution:
Let p(x) = x5 - 4x3 + x2 + 3x + 1 (Dividend)
g(x) = x3 + 0x2 - 3x + 1 (Divisor)
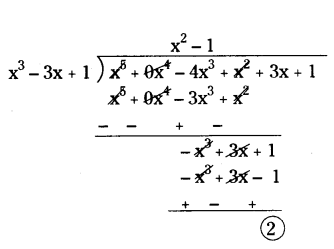
So, quotient q(x) = x2 - 1
remainder r(x) = 2
Therefore, g(x) = x3 - 3x + 1 is not a factor of p(x) = x5 - 4x3 + x2 + 3x + 1
Question 10.
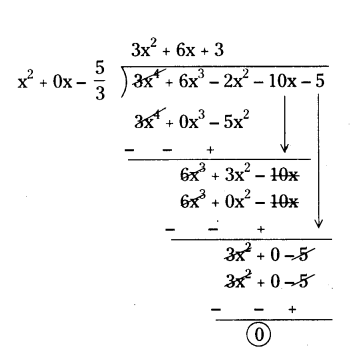
Obtain all other zeroes of 3x4 + 6x3 - 2x2 - 10x - 5, if two of its zeroes are √5/3 and √5/3
Solution:
Given, p(x) = 3x4 + 6x3 - 2x2 - 10x - 5
Two zeroes are √5/3 and - √5/3
That is (x - √5/3) and (x + √5/3)
∴ g(x) = (x - √5/3) (x + √5/3) = (x2 - 5/3) is a factor of p(x).

Question 11.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
i) deg p(x) = deg g(x)
ii) deg q(x) = deg r(x)
iii) deg r(x) = 0
Solution:
i) deg p(x) = deg g(x)
Let p(x) = 12x2 + 8x + 24, deg p(x) = 2
g(x) = 3x2 + 2x + 6, deg g(x) = 2
By division algorithm
we have p(x) = q(x) . g(x) + r(x)
So, divide p(x) by g(x)
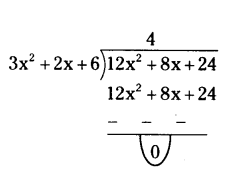
∴ q(x) = 4 and r(x) = 0
ii) deg q(x) = deg r(x)
Let p(x) = 6x3 + 11x2 - 39x - 65, deg p(x) = 3
g(x) = x2 + x - 1, deg g(x) = 2
By division algorithm,
p(x) = q(x) . g(x) + r(x)
So, divide p(x) by g(x).
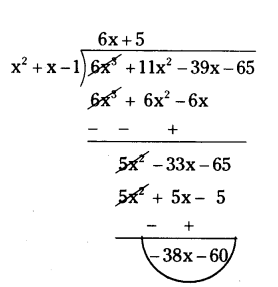
∴ q(x) = 6x + 5, deg q(x) = 1
r(x) = - 38x - 60, deg r(x) = 1
iii) deg r(x) = 0
Let p(x) = 3x2 - x3 - 3x + 5, deg p(x) = 3
g(x) = x - 1 - x2, deg g(x) = 2
By division algorithm,
p(x) = q(x) . g(x) + r(x)
So, divide p(x) by g(x).
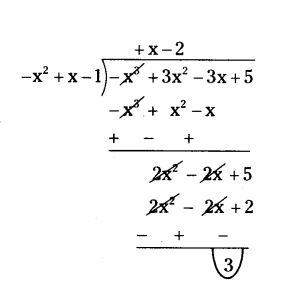
∴ q(x) = x - 2, deg q(x) = 1 and r(x) = 3, deg r(x) = 0
Question 12.
Verify that the numbers given along side of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case.
i) 2x3 + x2 - 5x + 2; (1/2, 1, -2)
ii) x3 + 4x3 + 5x - 2; (1, 1, 1)
Solution:
i) Given, p(x) = 2x3 + x2 - 5x + 2 and zeroes are 1/2, 1 and -2.
By comparing p(x) with ax3 + bx2 + cx + d
We get a = 2, b = 1, c = -5, d = 2
If x = 1/2, then
P(1/2) = 2(1/2)3 + (1/2)2 + (-5)(1/2) + 2
= 1/4 + 1/4 + 5/2 + 2/1
= 1+1-10+8/4 0/4 = 0
If x = 1, then
P(1)= 2(1)3 + 1(1)2 + (-5)(1) + 2
= 2 + 1 - 5 + 2 = 0
If x = -2, then
p(-2) = 2(-2)3 + 1 (-2)2 + (-5)(-2) + 2
= 2(-8) + 1(4) + 10 + 2
= -16 + 4 + 10 + 2 = 0
∴ 1/2, 1 and -2 are zeroes of
p(x) = 2x2 + x2 - 5x + 2
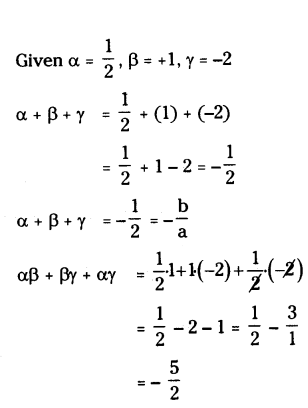
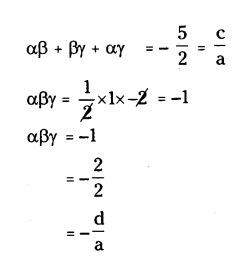
ii) Given p(x) = x3 + 4x2 + 5x - 2 and zeroes are 1, 1 and 1.
By comparing p(x) with ax3 + bx2 + cx + d
We get a = 1, b = 4, c = 5 and d = -2
If x = 1, then
p(1) = 1(1)3 + 4(1)2 + 5(1) + (-2)
= 1 + 4 + 5 - 2
= 10 - 2 = 8
∴ 1,1 and 1 are not zeroes of the given polynomial p(x).
Question 13.
If two zeroes of the polynomial x4 - 6x3 - 26x2 + 138x - 35 are 2 ± √3, find other zeroes.
Solution:
Given p(x) = x4 - 6x3 - 26x2 + 138x - 35 and two zeroes are 2 + √3 and 2 - √3.
Let other zeroes are α, β.
Sum of the zeroes
= 2 + √3 + 2 - √3 + α + β = -b/a = -(-6)/1 = 6
⇒ 4 + α + β = 6 ⇒ α + β = 6 - 4
⇒ α + β = 2 .... (1)
Product of zeroes
= (2 + √3) + (2 - √3)(α).(β) = c/a = -35/1
⇒ (4 - 3) α.β = -35
⇒ α.β = -35 ..... (2)
We know, (α - β)2 = (α + β)2 - 4αβ
(α - β)2 = 22 - 4(-35) = 4 + 140
α - β = √144 = ± 12 .... (3)
From (1) and (3)
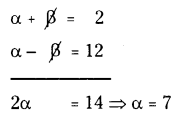
then a + β = 2 ⇒ 7 + β = 2
∴ β = 2 - 7 = -5
∴ Zeroes of polynomial x4 - 6x3 - 26x2 + 138x - 35 are 2 + √3, 2 - √3, 7 and -5.
Question 14.
If the polynomial x4 - 6x3 - 16x2 + 25x + 10 is divided by another polynomial x2 - 2x + k the remainder come out to be x + a, find k and a.
Solution:
Given, p(x) = x4 - 6x3 - 16x4 + 25x + 10
divisor g(x) = x4 - 2x + k
and r(x) = x + a
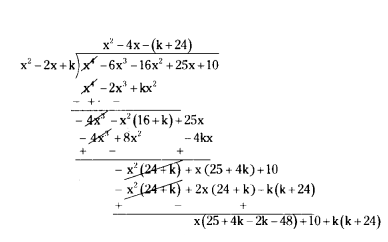
Remainder
⇒ x(4k + 25 - 2k - 48) + 10 + k(k + 24)
⇒ x(2k - 23) + (k3 + 24k + 10) = (x + a)
By comparing coefficients of x and constant term on both sides.
2k - 23 = 1
2k = 1 + 23
k = ± 24/2 = 12
k2 + 24k + 10 = a
(12)2 + 24(12) + 10 = a
144 + 288 + 10 = a
a = 442
∴ k = 12 and a = 442.
Question 15.
Find the zeroes of the polynomial x2 - 2 + 1/6 x and verify the relation between the coefficients and zeroes of the polynomial.
Solution:
Let p(x) = x2 - 2 + 1/6 x
= x2 + x/6 - 2
Let p(x) = 0
x2 + x/6 - 2 = 0
⇒ 6x2 + x - 12 = 0 × 6
⇒ 6x2 + x - 12 = 0
⇒ 6x2 + 9x - 8x - 12 = 0
⇒ 3x(2x + 3) - 4 (2x + 3) = 0
⇒ (2x + 3) (3x - 4) = 0
⇒ 2x + 3 = 0 (or) 3x - 4 = 0
∴ x = -3/2 (or) x = 4/3
Verification :
Sum of zeroes = -3/2 + 4/3
= 9+8/6 = -1/6
Product of zeroes = -3/2 × 4/3 = -2 = -2
On comparing with ax2 + bx + c,
a = 6, b = 1, c = -12
α + β = -b/a × -1/6
αβ = c/a × -12/6 = -2
Hence verified.
AP 10th Class Maths 3rd Lesson Important Questions and Answers Polynomials
Question 1.
If p(x) = x2 - 5x - 6; find the value of p(3).
Solution:
p(x) = x2 - 5x - 6 (given) .
p(3) = 32 - 5(3) - 6
= 9 - 15 - 6
= 9 - 21
= -12
So p(3) = - 12.
Question 2.
Write two more pdjmmilak and create two questions for each of them.
Solution:
i) x2 - 5x + 6 (polynomial (i)}
Questions:
1) What is the order of the polynomial ?
2) What are the zeroes of the polynomial?
ii) x2 - (4x) (polynomial (ii))
Questions:
1) How many zeroes are there to this polynomial ?
2) Do this polynomial has ∵0∵ as its zero value ?
Question 3.
If p(y) = y3 - 1, then verify that 1, -1 are the zeroes of p(y) or not.
Solution:
p(y) = y3 - 1
p(1) = 13 - 1 = 1 - 1 = 0
∴ ∴1∵ is the zero of p(y).
p(-1) = (-1) - 1 = -1 - 1 = -2
∴ ∴-1∵ is not zero of p(y).
Question 4.
For what value of k, is 3 a zero (tf the polynomial 2x2 + x + k
Solution:
Since 3 is a zero of the polynomial p(x) = 2x2 + x + k,
p(3) = 0
∴ p(3) = 2(3)2 + 3 + k = 0
⇒ 21 + k = 0
⇒ k = -21
Question 5.
Find the remainder when
7x5 - 3x2 + 5x - 2 is divided by x + 2.
Solution:
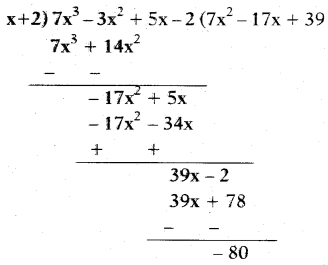
∴ Remainder = - 80
Question 6.
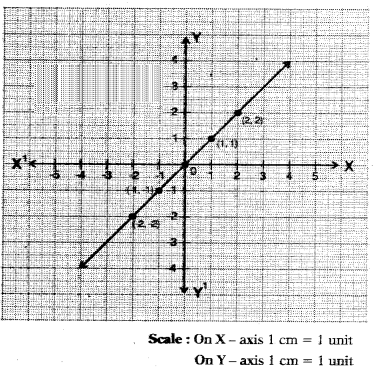
Draw a rough graph of x - y = 0.
Solution:
| x |
y |
(x, y) |
| 0 |
0 |
(0,0) |
| 1 |
1 |
(1, 1) |
| -1 |
-1 |
(-1, -1) |
| -2 |
-2 |
(-2, -2) |
| 2 |
2 |
(2, 2) |
Question 7.
Find the quadratic polynomial, whose zeroes are 2/3 and 2.
Solution:
Let the quadratic polynomial be
ax2 + bx + c, a ≠ 0 and its zeroes be α and β.
Here α = 2/3 and β = 2.
Sum of the zeores = α + β = 2/3 + 2 = 8/3
Product of the zeroes = αβ = 2/3 (2) = 4/3
∴ The quadratic polynomial
ax2 + bx + c is = [x2 - (α + β)x + αβ]
= [x2 - 8/3 x + 4/3]
The quadratic polynomial will be 3x2 - 8x + 4.
Question 8.
Find the zeroes of the quadratic poly-nomial 5x2 -4 - 8x and verify the rela-tion between the zeroes and its co-efficients.
Solution:
Given polynomial is 5x2 - 4 - 8x
= 5x2 - 8x - 4
= 5x2 - 10x + 2x - 4
= 5x(x - 2) + 2(x - 2)
= (x - 2) (5x + 2)
To find zeroes, (x - 2) (5x + 2) = 0
⇒ x - 2 = 0 or 5x + 2 = 0
⇒ x = 2 or x = - 2/5

Question 9.
Write the quadratic polynomial, whose sum of zeroes is -3 and sum of the i of zeroes is 17.
Solution:
The general form of quadratic polynomial having α,β as its zeroes is
= x2 - (sum of zeroes)x + product of zeroes.
= x2 - (α + β) x + αβ,
here given (α + β) = -3 and
(α2 + β2) = 17
∴ (α + β)2 = α2 + β2 + 2αβ
(-3)2 = 17 + 2αβ => 2αβ = 9 - 17 = -8
∴ αβ = - 8/2 = -4
∴ The required polynomial is x2 - (-3) x + (-4) = x2 + 3x - 4 is required quadratic polynomial.
Question 10.
if p and q are the zeroes of the poly¬nomial 3x2 - 5x + 2, write the polynomial in ∴x∵ whose zeroes are 1/p and 1/q
Solution:
It is given that, p and q are zeroes of polynomial 3x2 - 5x + 2.
Sum of zeroes = p + q = -(-5)/3 = 5/3 .....(1)
Product of zeroes = pq = = 2/3 .....(2)
Now we have to find the polynomial zeroes of which are 1/p and 1/q
 Hence required polynomial is 2x2 - 5x + 3.
Hence required polynomial is 2x2 - 5x + 3.
Question 11.
Solve the quadratic; polynomial x2 - 3x - 4 by graphical method.
Solution:
Let y = x2 - 3x - 4
For finding the points to draw y = x2 - 3x - 4
For plotting the points and drawing the graph.
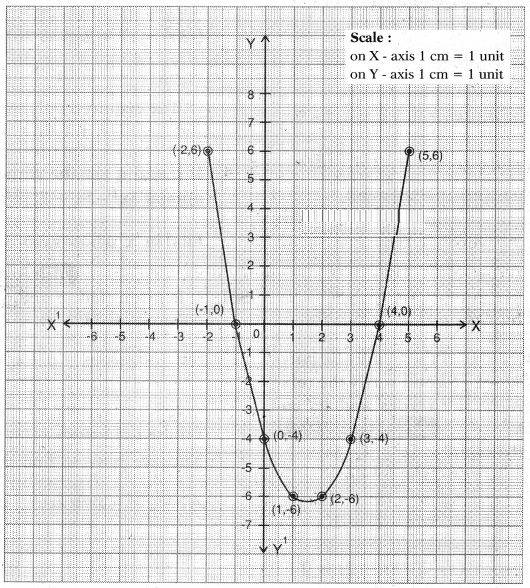
Note : The limitations of the solution in the problem need not be considered and award the marks for drawing the graph.
Question 12.
Draw the graph of polynomial 4x2 + 4x - 3 and find the zeroes, using the graph.
Solution:
To find the zeroes of the polynomial 4x2 + 4x - 3 by graph method. We need to find the points that lie on the curve.

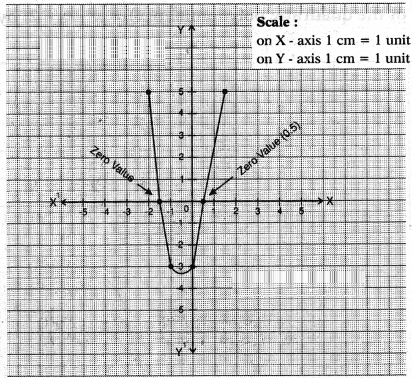
So zero values of y = 4x2 + 4x - 3 are 0.5 and -1.5
We observe the above curve passes through the points (0.5, 0) and (-1.5, 0) which are on x-axis.
Hence the zeroes of above polynomials are 0.5 and - 1.5.
Question 13.
Find the zeroes of the quadratic polynomial p(x) = x2+ x - 20 using graph.
Solution:
Given polynomial = p(x) = x2 + x - 20
List of values of p(x) :
Now let∵s locate the points listed above on a graph paper and join them free hand.
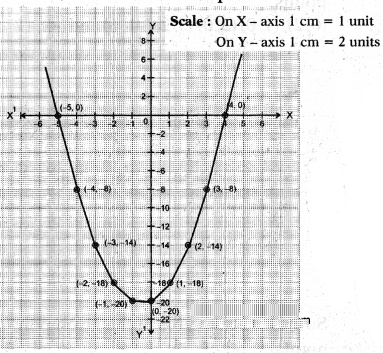
Result: We observe that the graph cuts the x-axis at (4, 0) and (-5, 0).
So, the zeroes of the given polynomial are 4 and -5.
Justification : Given p(x) = x2 + x - 20
⇒ x2 + 5x - 4x - 20 = 0
⇒ x(x + 5) - 4(x + 5) = 0
⇒ (x + 5) (x - 4) = 0
⇒ x = -5 dnd x = 4
Question 14.
Find the zeroes of the quadratic polynomial p(x) = x2 - x - 2, by using the graph.
Solution:
Let y = x2 - x - 2
Zeroes of the polynomial are 2,-1.
Question 15.
Draw the graph of polynomial
p(x) = x2 - 3x + 2 and find the zeros from the graph. June 2019
Solution:
Let y = p(x) = x2 - 3x + 2
If x = 0 then p(0) =0-0 + 2 = 2 So (0, 2)
x = 1 then p(1) = 12 + 3(1) + 2
= 1 - 3 + 2
= 0 So (1, 0)
x = 2 then p(2) = 22 - 3(2) + 2 = 4 - 6 + 2 = 0 So (2, 0)
x = 3 then p(3) = 32 - 3(3) + 2 = 9 - 9 + 2 = 2 So (3, 2)
and if x = -1 then p(-1)
= (-1)2 - 3(-1) + 2 = 1 + 3 + 2 = 6. So (-1, 6)
x = -2 then p(-2) = (-2)2 - 3 (-2) + 2 = 4 + 6 + 2= 12
So (-2, 12) that means the graph of the polyno¬mial
p(x) = x2 - 3x + 2 passes through the points.
(0,2), (1,0) (2,0) (3, 2) (-1,6) and (-2,12)
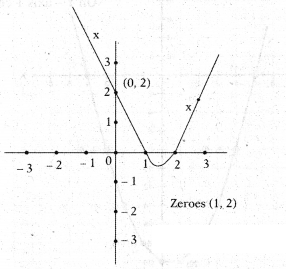
So 1 and 2 are zeros of the given polynomial.
Question 16.
Find the zeroes of x2 + 8x + 15.
Solution:
x2 + 8x + 15 = x2 + 5x + 3x + 15
= x(x + 5) + 3(x + 5)= (x + 3) (x + 5)
∴ -3,-5 are zeroes of the polynomial x2 + 8x + 15.
Question 17.
How do you say that the maximum number of zeroes of x2 + 8x + 15 is 2 ?
Solution:
The order of polynomial x2 + 8x + 15 is 2. Hence the maximum number of zeroes of it is 2.
Since the maximum possible zeroes of a polynomial is equal to its order.
Question 18.
Find the zeroes of x2 + 8x + 15 using graph.
Solution:
The zeroes of a polynomial are the X-coordinates of the points. Where its graph touches X-axis. Now let us find the points to draw the graph.
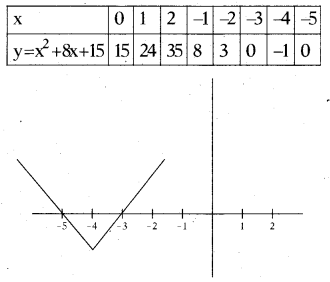
So the graph of polynomial x2 + 8x + 15 passes through the points (0, 15),
(1, 24), (2, 35), (-1, 8), (-2, 3), (-3, 0) and (-4, -1), (-5, 0)
The adjacent graph intersect the X-axis at - 3 and - 5.
Hence they are zeroes of it.
Question 19.
Check whether ∴6∵ becomes a zero of
x
2 + 8x + 15 or not ? Give reasons.
Solution:
If p(k) = 0 then ∴k∵ is a zero value of p(x)
Now p(x) = x2 + 8x + 15 then
p(6) = 62 + 8 (6) + 15
= 36 + 48 + 15 ≠ 0
As p(6) ≠ 0, ∴6∵ cannot be the zero value of p(x).
Question 20.
8 times of a number is added to its square give a result - 15. Then find the number by using its quadratic equation.
Solution:
Let us consider the given number = x
Then its square = x2
8 times of it = 8x
Now adding the above two x2 + 8x
result is = - 15
x2 + 8x = -15
x2 + 8x + 15 = 0
x2 + 5x + 3x + 15 = 0
⇒ x(x + 5) + 3(x + 5) = 0
⇒ (x + 3) (x + 5) = 0
∴ x + 3 = 0 or x + 5 = 0
Then x = - 3 or - 5
Question 21.
In how many points will the graph of x2 + 8x + 15 intersect X-axis ? Why ?
Solution:
We can write x2 + 8x + 15 as x2 + 5x + 3x + 15
⇒ (x + 5) (x + 3)
So its zero values are -5, -3
So the graph of x2 + 8x + 15 intersect x-axis at two points only.
Question 22.
Express the polynomial x2 + 8x + 15 in view of variable ∴y∵.
Solution:
y = x2 + 8x + 15
= x2 + 5x + 3x + 15
= x (x + 5) + 3 (x + 5)
y = (x + 3) (x + 5)
Question 23.
State the relation between coefficient of polynomials and zeroes of it.
Solution:
The polynomial is x2 -1- 8x + 15

Question 24.
Find p(3) if p(x) = x2 - 5x + 6 is given.
Solution:
p(x) = x2 - 5x + 6 (given)
then p(3) = 32 - 5(3) + 6
= 9 - 15 + 6 = 15 - 15 = 0
∴ P(3) = 0
AP 10th Class Maths 2nd Lesson Important Questions and Answers Sets (Old Syllabus)
Question 1.
Write roster and builder form of "The set of all natural numbers which di-vide 42".
Solution:
Factors of 42 = 1, 2, 3, 6, 7, 14, 21, 42
So roster form = {1, 2, 3, 6, 7, 14, 21, 42}
The builder form = {x/x ∈ N, x is a factor of 42}
Question 2.
Write A = {1, 2, 3, 4} in set builder form.
Solution:
The given set A = {1, 2, 3, 4}
The set builder form is A = {x/x ∈ N, x < 5}
Question 3.
Write all the subsets of B = {p, q}
Solution:
{p}, {q}, {p, q} and { } are the subsets of the given set B = {p, q}
As the n(B) = 2 then number of all sub-sets = 2n = 22 = 4
Question 4.
Write the following set {x : x = 2n + 1 and n ∈ N} in roster form.
Solution:
If n = 1 then 2n + 1 = 2(1) + 1
= 2 + 1 = 3
If n = 2 then 2n + 1 = 2(2) + 1
= 4 + 1 = 5
If n = 3 then 2n + 1 = 2(3) + 1 ∴
= 6 + 1 = 7
So {3, 5, 7, 9, } is the roster form of given set.
Question 5.
Give any two examples of disjoint sets from your daily life. 1161
Solution:
I) A∵ is set of Boys bom on Sunday
, ∴B∵ is set of Boys born on Monday
Then A and B disjoint sets
∵ A ∩ B = Φ
II) P is a set of all Indians .
Q is a set of all Russians
then P ∩ Q = Φ
Hence P, Q are disjoint sets.
Question 6.
If A = {Prime numbers less than 10}, and B = {Positive odd numbers less than 10}, then find (i) A ∩ B (ii) B - A.
Solution:
A = {Prime numbers less than 10} and
B = {Positive odd numbers less than 10}
∴ A = {2, 3, 5, 7},B = {1,3,5, 7, 9}
∴ (A ∩ B) = {2, 3, 5, 7} ∩ {1,3, 5,7, 9} = {3,5,7} - (1)
and (B - A) = {1, 3, 5, 7, 9} - {2,3, 5,7} = {1,9} --(2)
Question 7.
Write A = {3, 9,27, 81} in set - builder form.
Solution:
A = {x/x = 3n, n ∈ N and n < 5}
Question 8.
Write A = {2, 4, 8, 16} in set-builder form.
Solution:
Given set A = {2, 4, 8, 16}
Set builder form of A = {2x/x ∈ N, x < 5}
Question 9.
If A = {1/2,1/4,1/8,1/16,1/32} then write it in set-builder form.
Solution:
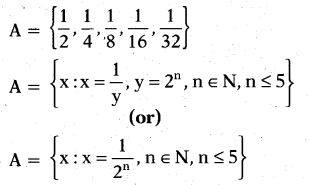
Question 10.
Write the set builder form of A = {1,1/4,1/9,1/16,1/25}
Solution:
{1,1/4,1/9,1/16,1/25} are in the form of 1/p2 whereas p < 6
So, A = {x : x = {x : x = 1/p2; p ∈ N, and p < 6} is the set builder form.
Question 11.
Given A = {x : x is an even number less than 10}
B = {x : x is a prime number Less than 10} find A ∩ B.
Solution:
Given A = (x : x is an even number less then 10}
∴ A = {2,4, 6, 8}
and B = {x : x is a prime number less than 10}
∴ B = {2, 3, 5, 7}
A ∩ B = {2,4, 6, 8} ∩ {2, 3, 5, 7}
∴ A ∩ B = {2}
Question 12.
Set A is a sub set of set B. If n(A) = 4 and n(B) = 7, then find n(A ∪ B).
Solution:
A ? B; n(A) = 4 and n(B) = 7
n(A ∪ B) = 7
Question 13.
Give one example for each question to set A and B, such that
i) A ∪ B = B, ii) A ∩ B = B.
Solution:
i) Let A = {1, 2, 3} and
B = {1,2,3,4, 5}
A ∪ B = {1,2, 3} ∪ {1, 2, 3, 4, 5}
= {1,2, 3,4, 5} = B
∴ A ∪ B = B
ii) Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10,..}
B = {2, 4,∵6, 8, 10, ...}
A ∩ B = {1, 2, 3, 4, 5, 6, 7, 8,9,10,..} ∩ {2, 4, 6, 8, 10, .}
= {2, 4, 6, 8, 10, ...} = B
∴ A ∩ B = B
Question 13.
If A = {5, 6, 7}, B = {6, 7, 8, 9} find A - (A - B) and A ∩ B. What is your observation?
Solution:
A = {5, 7}, B = {6, 7, 8, 9}
A - B = {5, 6, 7} - {6, 7, 8, 9}
= {5, 6, 7, 8, 9} = {5}
A - (A - B) = {5, 6, 7} - {5} = {6, 7}
A ∩ B - {5, 6, 7} ∩ {6, 7, 8, 9} = {6, 7}
We observe that A - (A - B) = A ∩ B.
Question 14.
Read the diagram and answer the questions given below.
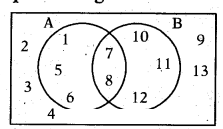
Find:
i) A ∪ B
ii) A - B
Solution:
i) A ∪ B = {1, 5, 6, 7, 8, 10, 11, 12}
ii) A - B = {1, 5, 6}
Question 15.
Let A = {x/x is an even number}
B = {x/x is an odd number}
C - {x/x is a prime number}
D = {x/x is a multiple of 5} Find
i) A ∪ B, ii) A ∩ B iii) C - D iv) A ∩ C.
Solution:
A = {x : x is an even number}
= {2,4,6,8,10 }
B = {x : x is an odd number}
= {1/3, 5,7,9, }
C = {x ; x is a prime number}
= {2,3,5,7,11, }
D = {x : x is a multiple of 5}
= {5, 10, 15, 20, 25, }
i) A ∪ B = {2, 4, 6, 8, 10, }∪{1,3, 5, 7, 9, .....}
= {1,2,3,4,5,6,7,8,9,10..}
ii) A ∩ B = {2, 4, 6, 8, 10, ..... } ∩ {1,3, 5, 7,9, ... }
= {} = Φ
iii) C - D = {2, 3, 5, 7, 11, .....} - {5, 10, 15, 20, 25, ..... }
= {2,3,7, 11, ..... }
iv) A ∩ C = {2, 4, 6, 8, 10, ...... } ∩{2,3,5,7,11 ...... }
= {2}
Question 16.
If A = {1,2,3, 4} and
B = {I, 2, 3, 5, 6} then find
i) A ∩ B, ii) B ∩ A iii) A - B and iv) B - C then comment on the above
Solution:
Given A = {1, 2, 3, 4} and
B = {1, 2, 3, 5, 6} then
i) A ∩ B = {1, 2, 3, 4} ∩ {1, 2, 3, 5, 6}
= {1,2,3}
ii) B ∩ A= {1,2, 3, 5, 6} ∩ {l,2, 3, 4}
= {1,2, 3}
So A ∩ B = B ∩ A
iii) A - B = {1,2, 3, 4} - {1,2, 3, 5,6}
= {4}
iv) B - A= {1,2, 3, 5, 6} - {1,2, 3, 4}
= {5,6}
So A - B ≠ B - A.
Question 17.
If A = {x : x is natural number}, B = {x: x is an even natural number}, C = {x, x is an odd natural number}, then find A ∩ B, A ∩ C, A - B, A - C and describe sets in set builder form.
Solution:
A = {1, 2, 3, 4, .....}
B = {2,4, 6, 8, ...... }; C = {1,3,5,7, ...... }
For finding,
A∩B = {1,2,3,4, } ∩ {2,4,6,8, .. }
= {2, 4, 6, 8..... }
= {x/x is an even natural number}
For finding,
A ∩ C = {1,2,3,4,...} ∩ {1,3,5,7, .... }
= {1,3,5,7 :...}
A = {x/x is an odd natural number}
For findging
A - B = {1,2,3,4, ..... } - {2,4,6,8, ..... }
= {1,3,5, ...... }
= {x/x is an odd natural number}
For finding
A - C = {1,2,3,4,...}-{1,3,5,7, }
= {2,4,6,8, ,.}
= {x/x is an even natural number}
Question 18.
If A = {3, 6, 9, 12, 15, 18,21},
B = {4, 8, 12, 16, 20}; then check whether A ∪ B = B ∪ A and A - B = B - A
Solution:
A ∪ B = {3,6,9,12,15,18,21}∪ {4,8,12,16,20}
= {3,4,6,8,9,12,15,16,18,20,21}
B ∪ A = {4,8,12,16,20} ∪ {3,6,9,12,15,18,21}
= {3,4,6,8,9,12,15,16,18,20,21}
A ∪ B = B ∪ A
A - B = {3,6,9,12,15,18,21} - {4,8,12,16,20} = {3,6,9,15,18,21}
B - A= {4,8,12,16,20} - {3,6,9,12,15,18,21} = {4,8,16,20}
A - B ≠ B - A
Question 19.
If A = {x : x is a natural number }
B = {x : x is an even number}
C = {x : x is an odd number }
D = {x : x is a prime number} then find A∪B,A∩C,B∩C and B ∩ D. Wbat do you notice ?
Solution:
A = {x : x is a natural number}
= {1,2,3, , }
B = {x : x is an even number}
= {2,4,6, }
C = {x : x is an odd number} .
= {1,3,5, .}
D = {x : x is a prime number = {2,3,5, }
A ∪ B = {1, 2, 3 ....}{2, 4, 6...... }
= {1,2,3.....}
A ∩ C = {1, 2, 3..... } ∩ {1, 3, 5...... }
= {1, 3, 5...... }
B ∩ C = {2,4,6... }∩{1,3,5..... }
= {} = ø
B ∩ D = {2,4,6,.} ∩ {2,3,5,.} = {2}
Noticed that A∪ B = A
A ∩ C = C
Question 20.
If A = {x : x is a natural number less than is 6}
B = {x : x is a prime number which is a divisor of 60} ,
C = {x : x is an odd natural number less than 10}
D = {x : x is an even natural number which is a divisor of 48}
Then write roster form for all above sets and find
i) A ∪ B
ii) B ∩ C
iii) A - D
iv) D - B
Solution:
Given sets in roster form.
A= {1,2, 3,4, 5}, B = {1,2, 3, 5}
C = {1, 3, 5, 7, 9}
D = {2, 4, 6, 8, 12, 16, 24}
i) A∪B = {1,2,5,4,5} ∪ {l,2,3,5}
= {1,2,3,4,5}
ii) B ∩C = {l,2,3,5} ∩ {l,3, 5,7,9}
= {1,3, 5}
iii) A - D. = {1,2, 3, 4,5} - {2, 4, 6, 8, 12, 16, 24}
= {1,3,5}
iv) D - B = {2, 4, 6, 8, 12, 16, 24} - {1,2, 3, 5}
= {4,6,8,12,16,24}
Question 21.
If A = {x : x is an even natural number and x < 12},
B = {x : x is a natural number and divisor of 6},
then find i) (A ∪ B) - (A ∩ B),
ii) (A - B) ∪ (B - A) What do you notice ?
Solution:
A = {2, 4, 6, 8, 10}; B = {1, 2, 3, 6}
A ∪ B = {2, 4, 6, 8, 10} ∪ {1, 2, 3, 6}
= {1,2,3,4,6,8,10}
A ∩ B = {2, 4, 6, 8, 10} ∩ {1, 2, 3, 6}
= {2, 6}
(A ∪ B) - (A ∩ B) = {1, 2, 3, 4, 6, 8, 10} - {2,6} = {1,3,4,8,10}
A - B = {2,4, 6, 8, 10} -{1,2, 3, 6}. ∴
= {4, 8, 10}
B - A = {1,2, 3, 6}-{2, 4, 6, 8, 10}
= {1,3}
(A - B) ∪ (B - A)- {4, 8, 10} ∪ {1,3}
= {1,3,4, 8, 10}
Noticed that (A ∪ B) - (A ∩ B) = (A - B) ∪ (B - A)
Question 22.
If A = {x/x e W, x < 10}
B = {x/x is a factor of 10}
C = {12, 22, 32,102}, then
Find i) A ∪ B ii) A ∩ B iii) A - C iv) B - C
Solution:
Given A = {x/x e W, x < 10}
B = {x/x is a factor of 10}
C = {12, 22, 32, ...... 102},
So A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {1,2, 5, 10}
C = {1,4, 9,16,25,36,49,64, 81,100}
i) A ∪ B
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ∪ {1,2,5,10}
= {0, 1,2, 3, 4, 5, 6, 7, 8, 9, 10} ... (1)
ii) A ∩ B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} ∩ {1,2, 5, 10} = {1,2, 5} ...... (2)
iii) A - C = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} - {1,4,9,16,25,36,49, 64, 81, 100}
= {0, 2, 3, 5,6, 7, 8} ...... (3)
iv) B - C = {1, 2, 5, 10}- {1,4,9,16,25,36,49,64, 81, 100}
= {2, 5, 10} .....(4)
Question 23.
If A = {x:x is a prime number and x < 20} B = {x : x = 2x + 1, x ∈ W and x < 9), find i) A ∩ B
ii) B ∩ A
iii) A - B
iv) B - A What do you observe ?
Solution:
A = {2, 3, 5, 7, 11, 13, 17, 19}
B = {1, 3, 5, 7}
i) A ∩ B = {2, 3, 5, 7,11, 13,17,19} ∩ {1,3, 5,7}
= {3,5,7} .
ii) B ∩ A = {1, 3, 5, 7} ∩ {2, 3, 5, 7, 11, 13, 17, 19} = {3,5,7}
iii) A - B = {2, 3,5,7, 11, 13, 17, 19} - {1,3, 5,7}
= {2, 11, 13, 17, 19}
iv) B - A = {1,3,5, 7} - {2, 3, 5, 7, li; 13, 17, 19}
= {1}
∴ We observed A ∩ B = B ∩ A
A - B ≠ B - A
Question 24.
A = {- 2, 1, 3, 4, 5}, B = {7, 3, 5, 2, 8} and C = {- 2, 4, 5, 8, 9}.
Find the following sets.
i) A - (B ∪ C), ii) (A - B) ∩ (A - C).
What is your observation ?
Solution:
A = {-2, 1, 3, 4, 5}; B = {7, 3, 5, 2, 8}, C = {- 2, 4, 5, 8, 9}
i) A - (B ∪ C)
B ∪ C = {7, 3, 5, 2, 8} ∪ {- i, 4, 5, 8, 9} = {-2, 2, 3, 4, 5, 7, 8, 9}
A - (B ∪ C) = {-2, 1, 3, 4, 5}- {-2, 2, 3, 4, 5, 7, 8, 9}
= {1}
ii) (A - B) ∩ (A - C)
A - B = {-2, 1,3,4, 5} - {7, 3, 5, 2, 8} = {-2,1,4}
A - C ={-2,1,3,4,5} - { - 2,4, 5,8,9)
= {1, 3)
(A - B) ∩ (A - C)= {-2, 1,4} ∩ {1,3}
= {1}
∴ A - (B ∪ C) = (A - B) ∩ (A - C)
Question 25.
A = {Regular Polygons}, B = {Triangles} and C = {Quadrilaterals}. Find
i) A ∩ B ii) A ∩ C iii) A - B iv) A - C
Solution:
A = {Triangles, Quadrilaterals, Pentagon, Hexagon, Heptagon}
B = {Triangles}; C = {Quadrilaterals}
i) A ∩ B = {Triangles, Quadrilaterals, Pentagon, Hexagon, Heptagon} ∩ {Triangles} = {Triangles}
ii) A ∩ C = {Triangles, Quadrilaterals, Pentagon, Hexagon, Heptagon} ∩ {Quadrilaterals} = {Quadrilaterals}
iii) A-B = {Triangles, Quadrilaterals, Pentagon, Hexagon, Heptagon} - {Triangles} = {Quadrilaterals, Pentagon, Hexagon, Heptagon}
iv) A - C = {Triangles, Quadrilaterals, Pentagon; Hexagon, Heptagon} - {Quadrilaterals}
= {Triangles, Pentagon, Hexagon, Heptagon}