14th Lesson Probability Class 10 Important Questions with Solutions
10th Class Maths Probability 1 Mark Important Questions
Question 1.
Vineeta said that probability of impossible events is 1. Dhanalakshmi said that probability of sure event is ‘O’ and Sireesha said that probability of any event lies in between 0 and 1. In the above with whom will you agree ?
Answer:
Sireesha.
Question 2.
A page is opened at a random from a book containing 90 pages. Then find the probability of a page number is a perfect square.
Answer:
1/90
Question 3.
From the figure, find the probability of getting blue ball.
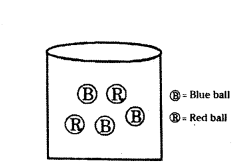
Answer:
3/5
Question 4.
If P(E) = 0.26, then find P (E) .
Answer:
0.74
Question 5.
Which of the following situations have equally likely events ?
Answer:
Getting 1 or 2 or 3 or 4 or 5 or 6 when a dice is rolled and winning or loosing a game and Head or Tail, when a coin is tossed.
Question 6.
If P(E) is the probability of an event E, then write the relation.
Answer:
0 ≤ P(E) ≤ 1
Question 7.
The probability of getting right answer to a question is 0.68, then find the
probability of getting a wrong answer.
Answer:
0.32 (or) 32%
Question 8.
Find the value of P(E) - 1 + p(E).
Answer:
0
Question 9.
From a well shuffled pack of cards, a card is drawn at random, then find the probability of getting a red jack.
Answer:
1/26
Question 10.
There are 50 cards numbered from to 50. A card is drawn at random, then find the probability that the number on the card is divisible by 8.
Answer:
3/25
Question 11.
A box contains pencils and pens. The probability of picking out a pen at random is 0.65. Then find the probability of not picking a pen.
Answer:
0.35
Question 12.
From a bag containing 6 red balls, 5 green balls and 3 blue balls, find the probability of getting a green ball at random.
Answer:
5/14
Question 13.
If E is an event whose probability is 2/5 then find the probability of not E.
Answer:
3/5
Question 14.
Three different greeting cards and their corresponding covers are randomly strewn about on a table. If Sita puts the greeting cards into the covers at random, find the probability of correctly matching of all the greeting cards and covers.
Answer:
1/6
Question 15.
If a ball is drawn at random from a box containing 11 red balls, 6 white balls and 9 green balls, then find the probability that the ball is not green.
Answer:
17/26
Question 16.
From a well shuffled pack of cards a card is drawn at random, then find the probability of getting a red coloured card.
Answer:
1/2
Question 17.
Find the probability of getting a number less than 5 when a die is rolled.
Answer:
2/3
Question 18.
If a card is drawn from a deck of 52 cards find the probability that it is a club card.
Answer:
1/4
Question 19.
In a single throw of two dice, find the probability of getting a total of 3 or 5.
Answer:
1/6
Question 20.
If two events have same chances to happen, then they are called which type of events ?
Answer:
Equally likely events.
Question 21.
Statement (A) : The probability of win-ning a game is 0.4, then the probability of losing it is 0.6.
Statement (B) : P(E) + P(not E) = 1
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 22.
Statement (A) : When two coins are tossed simultaneously, then the probability of getting no tail is 1/4.
Statement (B) : The probability of getting a head (i.e., no tail) in one toss of a coins is 1/2.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 23.
Statement (A) : In a simultaneously throw of a pair of dice. The probability of getting a double is 1/6.
Statement (B) : Probability of an event may be negative.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
ii) A is true, B is false
Question 24.
Statement (A) : If P(A) = 0.3 and P(A∪B)= 0.8, then P(B) is 2/7.
Statement (B) : P (E) = 1 - P(E), where E is any event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
i) Both A and B are true.
Question 25.
Statement (A) : If a box contains, 5 white, 2 red and 4 black marbles, then the probability of not drawing a white marble from the box is 5/11.
Statement (B) : p(E) = 1 - P(E), where E is any event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(iii) A is false, B is true.
Question 26.
Statement (A) : In rolling a dice, the probability of getting number 8 is zero.
Statement (B) : Its an impossible event.
i) Both A and B are true.
ii) A is true, B is false.
iii) A is false, B is true.
iv) Both A and B are false.
Answer:
(i) Both A and B are true.
Question 27.
Probability
A) 0.95
B) 0.02
C) -0.3
Written description
i) An incorrect assignment
ii) No chance of happening
iii) As much chance of happening as not
iv) Very likely to happen
v) Very little chance of happening
Answer:
A - (iv), B - (v), C - (i)
Question 28.
Probability
A) 0.5
B) 0
Written description
i) An incorrect assignment
ii) No chance of happening
iii) As much chance of happening as not
iv) Very likely to happen
v) Very little chance of happening
Answer:
A - (iii), B - (ii)
Question 29.
Written description
A) The probability of a sure event is
B) The probability of impossible event is
Probability
i) 0
ii) 1
iii) 2/7
iv) 12
v) 11/13
vi) 1/12
Answer:
A - (ii), B - (i)
Question 30.
A card is drawn from a well-shuffled deck of 52 cards randomly. What is the probability of getting a card, which is neither an ace nor a king card ?
Answer:
11/13
Question 31.
Write an example for sure event.
Answer:
When a die is thrown the event of getting a number less than or equal to 6.
Question 32.
What is the probability that 2022 have 53 Sundays ?
Answer:
1/7
Question 33.
The probability of getting a prime number in a single thrown of dice is _________ .
Answer:
3/6 or 1/2
Question 34.
If P(E) = 0.3, then P(not E) = __________
(A) 0.3
(B)
(C) 0
(D) 0.7
Answer:
D) 0.7 .
Question 35.
If P(E) = 0.4, then what is the probability of ‘not E’ ?
Answer:
Probability of ‘not E’ = 1 - P(E)
= 1 - 0.4 = 0.6
Question 36.
If P(E) = 0.7, then P(E) = ___________
Answer:
P(E) = 0.7
∴ P(E) = 1 - 0.7 = 0.3
Question 37.
If P(E) = 0.05, what is the probability of not‘E’?
Answer:
P(not E) = 0.95
Question 38.
If P(E) = 3/4, what is the probability of "not E" ?
Solution:
Probability P(E) = 3/4.
Prabability of "not E" P(E) = 1 - P(E)
= 1 - 3/4 = 1/4
Question 39.
When die is rolled once unbiased what is the probability of getting a multiple of 3 out of possible outcomes ?
Solution:
P(E) = Favourable outcomes/Total outcomes = 2/6 = 1/3
10th Class Maths Probability 2 Mark Important Questions
Question 1.
What is the probability that a number selected from the numbers 1, 2, 3,., 25 is a prime number, when each of the given numbers is equally likely to be selected ?
Solution:
Given the numbers : 1, 2, 3,., 25
Toted number of possible outcomes = 25
Prime numbers from 1 to 25 = 2, 3, 5, 7, 11, 13, 17, 19, 23
No. of prime numbers = 9
Let E be the event of probability of getting prime number from 1 to 25.
No. of favourable outcomes = 9
Now P(E) = No. of favourable outcomes/Total no.of possible outcomes
Therefore, P(E) = 9/25.
Question 2.
Tickets numbered from 1 to 20 are mixed up together and then a ticket is drawn at random. What is the probability that the ticket has a number which is a multiple of 3 or 7 ?
Solution:
Given numbers : 1, 2, 3,., 20
Total numbers = 20
Total no. of possible outcomes = 20
3 multiples from 1 to 20 = 3,6,9,12,15,18
7 multiples from 1 to 20 = 7, 14.
3 or 7 multiples = 3,6, 7,9,12,14,15,18
Total number of 3 or 7 multiples = 8
Let E be the event of probability of getting 3 or 7 multiples from 1 to.20.
No. of favourable outcomes = 8
Now P(E) = No. of favourable outcomes/Total no.of possible outcomes
= 8/20 = 2/5
Therefore, P(E) = 2/5.
Question 3.
Cards marked from the number 2 to 100 are placed in a box and mixed thoroughly. One card is drawn from this box. Find the probability that the number on the card is a number which is a perfect square.
Solution:
Given the numbers : 2, 3,., 100
No. of numbers = 99
Total number of possible events = 99
Perfect square numbers from 2 to 100 = 4, 9,16, 25, 36, 49, 64,81, 100
No. of perfect squares = 9
Let E be the probability of getting perfect square.
No. of favourable events = 9
Now P(E) = No. of favourable events/Total no. of possible events
= 9/99 = 1/11
Therefore, P(E) = 1/11.
Question 4.
An urn contains 10 red and 8 white balls. One ball is drawn at random. Find the probability that the ball drawn is white.
Solution:
Given urn contains 10 red and 8 white balls.
Total no. of balls 10 + 8 = 18
Total no. of possible outcomes = 18
Let E be the event of probability of getting white balls.
No. of white balls = 8
No. of favourable outcomes = 8
Now P(E) = No. of favourable outcomes/Total no. of possible outcomes
= 8/18 = 4/9
Therefore, P(E) = 4/9.
Question 5.
In a lottery there are 10 prizes and 25 blanks. What is the probability of getting a prize ?
Solution:
Given 10 prizes and 25 blanks
Total no. of card = 10 + 25 = 35
Total no. of possible outcomes = 35
Let E be the event of probability of getting prize.
No. of prizes = 10
No. of favourable outcomes = 10
Now, P(E) = Now P(E) = No. of favourable outcomes/Total no. of possible outcomes
= 10/35 = 2/7
Therefore, P(E) = 2/7 .
Question 6.
If the probability of winning a game is 0.3. What is the probability of loosing it ?
Solution:
Given the probability of winning a game is 0.3
That is P(winning) = 0.3
P(winning) + P(loosing) = 1
0.3 + P(loosing) = 1
P(loosing) = 1 - 0.1
Therefore, probability of loosing game = 0.9
Question 7.
The probability of an event is always in between 0 and 1. Why ?
Solution:
From the definition of probability P(E), the numerator (number of outcomes favourable to the event E) is always less than of equal to the denominator (the number of all possible outcomes).
So, the probability of an event is always in between 0 and 1.
i.e., 0 ≤ P(E) ≤ 1.
Question 8.
Find the probability of getting a sum of the numbers on them is 7, when two dice are rolled at a time.
Solution:
When two dice are rolled at a time the total outcomes are = 62 = 36
Number of outcomes such that their sum of numbers on face is 7 = 6
∴ Probability of getting sum of numbers on faces to be 7 = 6/36 = 1/6
Question 9.
Find the probability of getting a prime number, when a card drawn at random from the numbered cards from 1 to 25.
Solution:
Favourable outcomes of prime numbers from 1 to 25 = 9
Total number of outcomes = 25
Probability of getting a prime number
= Number of favourable outcomes/Total number of total outcomes = 9/25
Question 10.
From the first 50 natural numbers, find the probability of randomly selected number is a multiple of 3.
Solution:
Multiples of 3 from 1 to 50
3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48
No. of favourable outcomes to get multiples of 3 from 1 to 50 = 16
Probability of getting multiple of 3 from 1 to 50
= No. of favourable outcomes/No. of total outcomes = 16/50 = 8/25.
Question 11.
A dice is thrown once. Find the probability of getting a composite number.
Solution:
Possible outcomes = 1, 2, 3, 4, 5, 6
Favourable outcomes = 4, 6
Probability of a getting a compositive number
= Number of favourable outcomes/Total possible outcomes
= 2/6 = 1/3.
Question 12.
What is the probability of getting exactly two heads, when three coins tossed simultaneously ?
Solution:
Probability of getting exactly two heads
= number of favourable out comes/total number of out comes
= 3/8
Question 13.
From English alphabet if a letter is choosen at random, then find the probability that the letter is a consonant.
Solution:
Number of total outcomes = 26
Number of favourable outcomes = 21
Probability that the letter is consonant
= Number of favourable outcomes/Number of total outcomes = 21/26
Question 14.
If a dice is rolled once, then find the probability of getting an odd number.
Solution:
Total outcomes = {1, 2, 3, 4, 5, 6}
Number of Total outcomes = 6
Favourable outcomes = {1, 3, 5}
Number of favourable outcomes = 3
P (an odd number)
= Number of favourable outcomes/Number of Total outcomes = 3/6 = 1/2
Question 15.
Find the probability of getting a ‘vowel’ if a letter is chosen randomly from the word "INNOVATION".
Solution:
P(E) = Number of favourable outcomes/Number of Total outcomes = 3/6 = 1/2
Favourable outcomes = i, o, a, i, o
Number of favourable outcomes = 5
Number of total outcomes = 10
P(getting a vowel) = 5/10 = 1/2
Question 16.
You are writing a test of 40 objective type questions. Each question carries 1 mark. What is the probability of marks you may get to be in multiple of 5 ?
Solution:
Total Number of questions = 40
Total Number of outcomes = 40
Number of Multiples of 5 upto 40 = 8
Favourable outcomes = 8
Probability for getting multiples of 5
= Favourable outcomes for getting multiples of 5/Total No. of possible outcomes
= 8/40 = 1/5
Question 17.
A page is opened at random from a book containing 100 pages. Find the probability that the page number is a perfect square.
Solution:
Number of pages in given book = 100
The page numbers that will be perfectly a square number (If randomly that are selected) are 1, 4, 9, 16, 25, 36, 49, 64, 81 and 100.
∴ Number of favourable outcomes = 100
Number of all possible outcomes = its number of pages = 100
∴ Probability of getting a perfect number = 10/100 = 0.1.
Question 18.
A box contains 3 blue and 4 red balls. What is the probability that the ball taken out randomly will be red ?
Solution:
Total number of balls in the box = 3 + 4 = 7
No. of favourable outcomes for picking a red ball = 4
∴ Probability of red ball
= Number of favourable outcomes/Total outcomes ∴ P(E) = 4/7
Question 19.
A three digit number is formed by the digits 2, 3 and 5 without repetition. What is the probability that the number is divisible by 5 ?
Let ’E’ be the event of choosing a three digit number divisible by 5.
All possible three digit numbers (without repetition) 235, 253, 325, 352, 523, 532.
∴ n(S) = 6; E = {235, 325}; n(E) = 2
∴ p(E) = 2/6 = 1/3
Question 20.
In a classroom, 32 students out of 60 can take tea. Find the probability of "The tea not taken".
Solution:
Total Number of possible outcomes = 60
No. of students doesn’t take tea (No. of favourable outcomes) = 60 - 32 = 28
Probability of students not taken tea
= No, of favourable outcomes for not taken tea/Total No. of possible outcomes = 28/60 = 7/15
Question 21.
If P(E) = 0.25, what is the probability of ‘not E’ ?
Solution:
Given P(E) = 0.25
Hence P(E) + P(E) = 1
Where P(E) is the probability of ‘not E’.
⇒ 0.25 + P(E) = 1
⇒ P(E) = 1 - 0.25 = 0.75.
Question 22.
Find the probability of getting the letter M in the word. "MATHEMATICS".
Solution:
Let the event of getting the letter M be E
Number of favourable outcomes to E = 2
Number of all possible outcomes = 11
∴ P(E) = No. of favourable outcomes to E/All possible outcomes = = 2/11
10th Class Maths Probability 4 Mark Important Questions
Question 1.
Find the probability that a leap year selected at random will contain 53 Sundays.
Solution:
In every year there are 365 days.
But in a leap year there are 366 days.
366 days = 52 weeks + 2 days.
So, every leap year 52 Sundays and the remaining 2 days can be possible in 7 events. They are,
1) Sunday and Monday
2) Monday and Tuesday
3) Tuesday and Wednesday
4) Wednesday and Thursday
5) Thursday and Friday
6) Friday and Saturday
7) Saturday and Sunday.
So, total no. of possible outcomes = 7
Let E be the event of probability of getting 53 Sundays.
No. of favourable outcomes = 2
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 2/7
Question 2.
It is known that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box. What is the probability that it is a non-defective bulb ?
Solution:
Given no. of bulbs in the box = 600
Total no. of bulbs = 600
Total no. of possible outcomes = 600
Let E be the event of probability of getting a non-defective bulb.
No. of defective bulbs = 12
No. of non-defective bulbs = 600 - 12 = 588
No. of favourable outcomes = 588
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
= 588/600 = 49/50
∴ P(E) = 0.98.
Question 3.
A letter is chosen at random from the letters of the word ASSASSINATION. Find the probability that the letter chosen is a
i) Vowel
ii) Consonant.
Solution:
In the given word "ASSASSINATION" there are 13 letters.
So, total no. of possible outcomes = No. of letters = 13
i) No. of vowels in the word = 6
No. of favourable outcomes = 6
Let E be the event of probability of getting vowel in the given word.
Now,P(E) = No. of favourable outcomes/Total no. of possible outcomes = 6/13
ii) No. of consonants in the word = 7
Let E be the event of probability of getting consonant in the given word. No. of favourable outcomes = 7
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 7/13
Question 4.
A jar contains 24 marbles some are green and other are blue. If a marble is drawn at random from the jar, the probability that it is green is 2/3. Find the number of blue marbles in the jar.
Solution:
Given the no. of marbles in the jar = 24
Let the no. of green marbles = x
The no. of blue marbles = 24 - x
Total no. of possible outcomes = 24
Let E be the event of probability of getting green marble.
No. of favourable outcomes of getting green marbles = x
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
Given P(E) = x/24 = 2/3
x = 2/3 × 24 = 16
No. of green marbles (x) = 16
No. of blue marbles = 24 - x = 24 - 16 = 8
Therefore, no. of blue marbles = 8.
Question 5.
A number of x is selected from the numbers 1, 2, 3 and then a second number 7 is randomly selected from the numbers 1, 4, 9. What is the probability that the product xy of the two numbers will be less than 9 ?
Solution:
Given a number x is selected from 1, 2, 3 and y is selected from 1, 4, 9
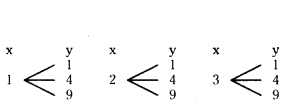
Therefore, two numbers can be selected in 9 ways as given below.
(x, y) as (1, 1), (1, 4), (1, 9), (2, 1), (2, 4), (2, 9), (3, 1), (3, 4), (3, 9)
So, total no. of possible outcomes = 9.
Let E be the event of probability of getting the product xy of the two numbers will be less than 9.
Favourable outcomes = (1, 1), (1, 4), (2, 1), (2, 4), (3, 1)
No. of favourable outcomes = 5
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 5/9.
Question 6.
What is the probability that a number selected from the numbers 1, 2, 3,., 15 is a multiple of 4 ?
Solution:
Given numbers : 1, 2, 3,., 15
Total numbers = 15
Total no. of possible outcomes = 15
4 multiples from 1 to 15 are 4, 8, 12
No. of 4 multiples = 3
No. of favourable outcomes = 3
Let E be the event of probability of getting 4 multiples
Now, P(E) No. of favourable outcomes/Total no. of possible outcomes
= 3/15 = 1/5
∴ P(E) = 1/5.
Question 7.
A number is selected at random from the first 50 natural numbers. Find the probability it is a multiple of 3 and 4.
Solution:
Given numbers : 1, 2, 3,., 50
Toted numbers = 50
Total no. of possible outcomes = 50
Multiples of 3 and 4 from 1 to 50 = 12, 24, 36,48
Let E be the event of probability of getting a number of multiple of 3 and 4.
No. of multiples of 3 and 4 = 4
No. of favourable outcomes = 4
Now, P(E) No. of favourable outcomes/Total no. of possible outcomes
= 4/50 = 2/25
∴ P(E) = 2/25.
Question 8.
There are 12 red, 18 blue and 6 white balls in a box. When balls is drawn at random from the box, what is the probability of not getting a red ball ?
Solution:
Total Number of balls = 12 + 8 + 6 = 36
Number of Red balls = 12
∴ Probability of getting Red ball P(R) = favourable outcomes/total outcomes = 12/36 = 1/3
∴ Probability of not getting Red ball
p(R) = 1 - 1/3 = 2/3
(Or)
Total Number of balls = 12 + 18 + 6 = 36
Exclude, the Red balls, the number of remaining balls = 18 + 6 = 24
Probability of not getting a Red ball = 24/36 = 2/3
Question 9.
When a card is drawn from a well shuffled deck of 52 cards, then find the probability of NOT getting a red faced card.
Solution:
Number of total outcomes = 52
Number of red face cards = 6
Probability of a red face card = 6/52.
∴ Probability of "NOT" getting a red face card = 1 - 6/52
= 52-6/52 = 46/52 = 23/26
Question 10.
There are 5 red balls, 4 green balls and 6 yellow balls in a box. If a ball is selected random, what is the probability of not getting a yellow ball ?
Solution:
Total number of balls in a bag = 15
Total number of chance to select a ball from a bag = 15
Favourable outcomes to select not yellow ball = 9
Probability of not getting a yellow ball = Number of favourable outcomes/Total number of outcomes = 9/15 = 3/5.
Question 11.
One card is selected from a well - shuffled deck of 52 cards. Find the probability of getting a red card with prime number.
Solution:
Number of cards in a deck = 52
Number of red card with prime number = 8
Probability of getting red card with prime number
P(E) = Number of favourable outcomes/Number of total outcomes = 8/52 = 2/13.
Question 12.
From the following data, find the prob-ability of selecting ‘B’ blood group student.
| Blood group |
A |
B |
AB |
O |
| Number of students |
10 |
13 |
12 |
5 |
Solution:
Number of favourable outcomes = 13
Number of total possible outcomes = 40
∴ Probability of selecting B blood group = No.of Favourable outcomes/No. of Total outcomes = 13/40
Question 13.
What is the probability of a number picked from first twenty natural numbers is even composite number ?
Solution:
Sample space = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ....... 20}
Favourable out comes = {4, 6, 8, 10, 12, 14, 16, 18, 20}
Probability of getting even composite number
from first twenty natural numbers = Number of favourable outcomes/Number of total outcomes = 9/20
Question 14.
A bag contains balls which are numbered from 1 to 50. A ball is drawn at random from the bag, the probability that it bears a two digit number multiple of 7.
Solution:
Number of possible outcomes = 50
Number of required outcomes = 6 {14, 21, 28, 35, 42, 49}
Probability of getting two digit number which is a multiple of 7 = Number of favourable outcomes/Number of total outcomes = 6/50 = 3/25
Question 15.
A box contains 4 red balls, 5 green balls and P white balls. If the probability of randomly picked ball from the box to be a red ball is 1/3, then find the number of white balls.
Solution:
P(E) = No. of outcomes/Sample Space
= 1/3 = 4/4+5+P
4 + 5 + P = 12 ⇒ P = 3
∴ Number of white balls = 3
Question 16.
A bag contains 7 red, 5 white and 6 black balls. A ball is drawn from the bag at random, find the probability that the ball drawn is not black.
Solution:
Number of total outcomes = 7 + 5 + 6 = 18
Number of favourable outcomes = 7 + 5 = 12
Probability that the ball dravn is not black = Number of favourable outcomes/Number of total possible outcomes
= 12/18 = 2/3
Question 17.
A box contains 20 cards which are numbered from 1 to 20. If one card is selected at random from the box, find the probability that it bears (i) a prime number, (ii) an even number.
Solution:
Total possibilities = {1, 2, 3, 4, 5, 6, 7, 8, 9, ...., 20}
Number of Total possibilities = 20
i) Prime numbers = {2, 3, 5, 7, 11, 13, 17, 19}
Number of favourable outcomes = 8
P(Prime Number) = Number of favourable outcomes/Total number of outcomes
= 8/20 = 2/5
∴ P(Prime Number) = 2/5
ii) Even numbers = {2, 4, 6, 8,10, 12, 14,16,18, 20}
Number of favourable outcomes = 10
P (Even Number) = Number of favourable outcomes/Total number of outcomes
= 10/20 = 1/2
∴ P(Even number) = 1/2
Question 18.
A box contains four slips numbered 1, 2, 3, 4 and another box contains five slips numbered 5, 6, 7, 8, 9. If one slip is taken randomly from each box,
i) How many number pairs are possible ?
ii) What is the probability of both being odd ?
iii) What is the probability of getting the sum of the numbers 10 ?
Solution:
i) Possible number pairs
(1, 5) (1, 6) (1, 7) (1, 8) (1, 9)
(2, 5) (2, 6) (2, 7) (2, 8) (2, 9)
(3, 5) (3, 6) (3, 7) (3, 8) (3, 9)
(4, 5) (4, 6) (4, 7) (4, 8) (4, 9)
Number of possible number pairs = 20
ii) Favourable outcomes (1, 5), (1, 7), (1, 9), (3, 5), (3, 7), (3, 9)
Number of favourable outcomes = 6
P(getting both being odd) = Number of favourable outcomes/Total number of outcomes
= 6/20 = 3/10
iii) Favourable outcomes (1, 9), (2, 8), (3, 7), (4, 6)
Number of favourable outcomes = 4
P(getting the sum of the numbers 10)
= 4/20 = 1/5
Question 19.
In a bag, there are 5 Red balls, 2 Black balls and 3 White balls. If one ball is selected randomly from the bag, then find the probability of -
i) getting a Red ball.
ii) getting not a Red ball.
Solution:
Red balls = 5
Black balls= 2
White balls = 3
Total balls = 5 + 2 + 3 = 10
Number of favourable
i) P(E) = outcomes/Total number of outcomes
P (getting a Red ball) = 5/10 = 1/2
ii) P (Not getting a Red ball) = Number of favourable outcomes/Total number of outcomes
= 2+3/10 = 5/10 = 1/2
Question 20.
There are 100 flash cards labelled from 1 to 100 in a bag. When a card is drawn from the bag at random, what is the probability of getting ...
i) a card with prime number from possible outcomes ?
ii) a card without prime number from possible outcomes ?
Answer:
Number of prime numbers between 1 and 100 = 25
i) Probability of getting a card with prime numbers = 25/100 = 1/4 = 0.25
ii) Probability of getting a card without prime number = 75/100 = 0.75
Question 21.
A shopkeeper has 100 memory cards in a box. Among them, 15 memory cards are defective. When a person came to the shop to buy a memory card, the shopkeeper drew a memory card at random from the box. Then,
i) what is the probability that this memory card is defective ?
ii) after drawing the first memory card which is defective, it is not placed back in the box. Then another memory card is drawn at random. What is the probability that this memory card is NOT defective ?
Solution:
i) Total all possible outcomes = n(T) = 100
Number of favourable outcomes = n(E) = 15
The probability that memory card is defective P(E) = n(E)/n(T) = 15/100 = 3/20
ii) Removed defective card is not placed in the box, so the probability that memory card is defective
= P(E’) = 14/100 = 7/50
The probability that memory card is
NOT defective = 1 - P(E’) = 1 - 7/50
= 50-7/50 = 43/50
Question 22.
A die is thrown once. Find the probability of getting (i) a prime number (ii) a number lying between 1 and 5.
Solution:
When a die is thrown once sample space = S = {1, 2, 3, 4, 5, 6}
Total number of outcomes = n(S) = 6
i) Let ‘E’ be an event of getting a prime number.
Favourable outcomes to E = {2, 3, 5}
n(E) = 3
∴ P(E) = n(E)/n(S) = 3/6 = 1/2
ii) Let ‘F’ be an event of getting a number lying between 1 and 5.
Favourable outcomes to F = {2, 3, 4}
n(F) = 3
∴ P(F) = n(E)/n(S) = 3/6 = 1/2
10th Class Maths Probability 8 Mark Important Questions
Question 1.
Two unbiased coins are tossed simultaneously. Find the probability of getting
i) two heads
ii) one head
iii) one tail
iv) atleast one head
v) at most one head
vi) no head
Solution:
If two unbiased coins are tossed simultaneously.
We get the outcomes HH, HT, TH, TT.
Total number of possible outcomes = 4.
i) Let E be the event of probability of getting two heads.
So, favourable outcomes = HH.
No. of favourable outcomes = 1
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 1/4
ii) Let E be the event of probability of getting one head.
So, favourable outcomes = HT, TH.
No. of favourable outcomes = 2
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 2/4 = 1/2
∴ P(E) = 1/2
iii) Let E be the event of probability of getting one tail.
So, favourable outcomes = TH, HT.
No. of favourable outcomes = 2
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 2/4 = 1/2
∴ P(E) = 1/2
iv) Let E be the event of probability of getting atleast one head.
So, favourable outcomes = HT, TH, HH
No. of favourable outcomes = 3
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 3/4
v) Let E be the event of probability of getting at most one head.
So, favourable outcomes . = HT, TH, HH
No. of favourable outcomes = 3
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 3/4
vi) Let E be the event of probability of getting no head.
So, favourable outcomes = TT
No. of favourable outcomes = 1
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 1/4
Question 2.
Find the probability that a number selected at random from the numbers 1, 2, 3,.., 35 is a
i) prime number
ii) multiple of 7
iii) a multiple of 3 or 5
Solution:
Given numbers are 1, 2, 3,.., 35
Total number of possible outcomes = 35
i) Let E be the event of probability of getting prime number.
Prime numbers from 1 to 35
= 2, 3, 5, 7,11,13,17, 19, 23, 29,31
No. of favourable outcomes = 11
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 11/35
ii) Let E be the event of probability of getting 7 multiple from 1 to 35.
7 multiples : 7, 14, 21, 28, 35
No. of favourable outcomes = 5
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 5/35 = 1/7
∴ P(E) = 1/7
iii) Let E be the event of probability of getting multiple of 3 or 5.
3 multiples
= 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33
5 multiples = 5, 10, 15, 20, 25. 30, 35
Favourable outcomes = 3, 5, 6, 9, 10, 12, 15, 18, 20, 21, 24, 25, 27, 30, 33, 35
No. of favourable outcomes = 16
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 16/35.
Question 3.
Cards marked with numbers 13, 14, 15 . 60 are placed in a box and mixed thoroughly one card is drawn at random from the box. Find the probability that number on the card drawn is
i) divisible by 5
ii) a number is a perfect square.
Solution:
Given number cards = 13, 14, 15,., 60
Total number of cards = 48
Total number of possible outcomes = 48
i) 5 multiples from 13 to 60 are: 15,20, 25, 30, 35, 40, 45, 50, 55, 60.
Let E be the event of probability of getting of 5 multiples.
No. of favourable outcomes = 10
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 10/48 = 5/24
∴ P(E) = 5/24
ii) Let E be the event of probability of getting a perfect square.
Perfect squares from 13 to 60 are 16, 25, 36, 49.
No. of perfect squares = 4
No. of favourable outcomes = 4
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 4/48 = 1/12
∴ P(E) = 1/12.
Question 4.
The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the probabili¬ty of getting a card of i) heart ii) queen iii) clubs
Solution:
Given king, queen and jack of clubs removed from deck.
Then number of cards remaining = 52 - 3 = 49
Total number of possible outcomes = 49
i) Let E be the event of probability of getting heart.
Number of cards of heart =13
No. of favourable outcomes = 49
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 13/49.
ii) Let E be the event of probability of getting queen.
No. of queens in the deck = 4
But, one queen clubs removed.
So, number of queens = 4 - 1 = 3
No. of favourable outcomes = 3
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 3/49.
iii) Let E be the event of probability of getting clubs.
No. of cards of clubs in the deck = 13
But, 3 cards (king, queen and jack) of clubs removed.
So, no. of cards of club = 13 - 3 = 10
No. of favourable outcomes = 10
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
∴ P(E) = 10/49.
Question 5.
A target shown in the given figure consists of three concentric circles of radii 3, 7 and 9 cm respectively. A dart is thrown and lands on the target. What is the probability that the dart will land on the shaded region ?
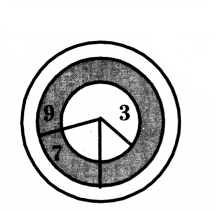
Solution:
Given radii of concentric circles 3 cm, 7 cm and 9 cm
Total area of the figure
= πr2 = π × 92 = 81π. sq. cm
Total possible area = 81π. sq. cm
Area of the circle of radius 3 cm
= π × 32 = 9π. sq. cm
Area of the circle of radius 7 cm
= π × 72 = 49π. sq. cm
Area of the shaded region
= 49π - 9π = (49 - 9) π = 40π. sq. cm
Let E be the probability of the dart land on the shaded region.
Favourable area = 40π. sq. cm
Now, P(E) = No. of favourable area/Total no. of possible area
= 40π/81π
∴ P(E) = 40/81.
Question 6.
A square dart board is shown in the figure. The length of a side of the larger square is 1.5 times the length of a side of the smaller square. If a dart is thrown and lands on the larger square. What is the probability that it will interior of the smaller square ?
Solution:
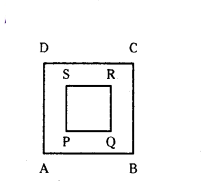
Given ABCD and PQRS are two squares.
Let side of square (PQRS) = x units.
Area of square PQRS = x.x = x2 sq. units.
Then side of the square ABCD = 1.5 times of x = 1.5 × x
Area of square ABCD = 1.5x × 1.5x = 2.25x2 sq. units.
Total possible area = 2.25x2 sq. units.
Favourable area of a dart get into the smaller square = x2 sq. units.
Let E be the event of probability of landing the dart into smaller square.
Now, P(E) = No. of favourable outcomes/Total no. of possible outcomes
P(E) = 1x2/2.25x2 = 1×100/2.25×100
= 100/225 = 4/9
∴ P(E) = 4/9.
Question 7.
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of red ball, find the number of blue balls in the bag.
Solution:
Number of red balls present in a bag = 5
Let the No.of blue balls = x (say)
Then the total No.of balls = 5 + x
From those (5 + x) balls in the bag
the number of favourable outcomes to take a red ball randomly = 5
So the probability of taking a red ball = 5/5+x
Now
The number of favourable outcomes to take a blue ball randomly = x
So the probability of taking a blue ball = x/5+x
From the given problem
Probability of blue bell = (Probability of red ball) (2)
x/5+x × 2
∴ x/5+x = 10/5+x ⇒ x = 10
∴ No. of blue balls in the bag = 10
Question 8.
From the deck of 52 cards, if a card is randomly chosen, find the probability of getting a card with (i) a prime number on it, (ii) face on it.
Solution:
The number cards in a deck = 52
Total number of outcomes = 52
i) Cards with a prime number on it = {2, 3, 5, 7} (in one suit)
Number of favourable outcomes = 4 × 4 = 16 (Q In each suit there are 4 cards with primes) Probability of getting a card with a prime number on it = Number of favourable outcomes/Total number of outcomes
= 16/52 = 4/13
ii) Number of face cards = 12
Number of favourable outcomes = 12
Probability of getting a face
card = Number of favourable outcomes/Total number of outcomes
= 12/52 = 3/13
Question 9.
Suppose you drop a dice at random on the circular region of diameter 28 cm as shown in the figure. What is the probability that it will land inside the rectangle ?
Solution:
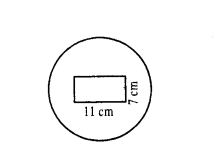
Diameter of circle = d = 28 cm
r = d/2 = 14 cm
Area of the circle = πr2
= 22/7 × 14 × 14
= 22 × 28 = 616 cm2
Area of the rectangle = l × b = 11 × 7 = 77 cm2
∴ Probability that it will land inside the rectangle = Area of the Rectangle/Area of the circle
= 77/616 = 7/56 = 1/8
Question 10.
A bag contains 20 discs, which are numbered from 1 to 20. If one disc is drawn at random from the bag, find the probability that it bears:
i) an even number,
ii) Prime number,
iii) Multiple of 5,
iv) Two digit odd number.
Solution:
Total number of possible outcomes = 20
i) For probability of the disc bears an even number
No. of favourable outcomes = 10 Probability = No. of favourable outcomes/Total No. of possible outcomes = 10/20 = 1/2
ii) For probability of the disc bears a prime number
No.of favourable outcomes = 8
Probability = 8/20 = 2/5
iii) For probability of the disc bears a multiple of 5
No. of favourable outcomes = 4
Probability = 4/20 = 1/5
iv) For probability of the disc bears a two digit odd number
No. of favourable outcomes = 5
Probability = 5/20 = 1/4
Question 11.
Two dice are thrown at the same time. What is the probability that the sum of two numbers appearing on the top of the dice is (a) 10, (b) less than or equal to 12, (c) a prime number, (d) multiple of ‘3’ ?
Solution:
Total number of possible outcomes when rolling two dice at a time = 6 × 6 = 36
Favourable outcomes of getting each sum is 10.
a) Sum be 10 = {(5, 5), (4, 6), (6, 4)}
No. of favourable outcomes = 3
∴ Required probability = P(E) = 3/36 = 1/12
(b) The outcomes favourable to the event
"Less than or equal to 12" be denotes by ‘F’ are
= {(1, 1) (1,2) (1, 3) (1, 4) (1, 5) (1, 6)
(2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6)
(3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6)
(4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6)
(5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6)
(6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)
No. of outcomes favourable to ‘F’ is n(F) = 36
∴ P(F) = n(F)/n(S) = 36/36 = 1
c) The outcomes favourable to the event "Sum of two numbers a prime number" be denoted by ‘G’ are (1, 1) (1, 2) (1, 4) (1, 6) (2,1) (2, 3) (2, 5) (3, 2) (3, 4) (4, 1) (4, 3) (5, 2) (5, 6) (6, 1) (6, 5)
No. of outcomes favourable to ‘G’ is n(G) = 15
∴ P(G) = n(G)/n(S) = 15/36 = 5/12
d) The outcomes favourable to the event "Sum of two numbers be multiple of 3" be denoted by ‘H’,are (1, 2) (1, 5) (2, 1) (2, 4) (3, 3) (3, 6) (4, 2) (4, 5) (5, 1) (5, 4) (6, 3) (6, 6)
No. of outcomes favourable to ‘H’ is n(H) = 12
∴ P(H) = n(H)/n(S) = 12/36 = 1/3
Question 12.
Two digit numbers are formed by the digits 0, 1, 2, 3, 4, where the digits are not repeated. Find the probability that
i) the number formed is greater than 42.
ii) the number formed is a multiple of 4.
Solution:
Two digit numbers formed by the digits 0, 1, 2, 3, 4
where the digits are not repeated
(10, 12, 13, 14, 20, 21, 23, 24, 30, 31, 32, 34, 40, 41, 42, 43)
∴ Sample space = (10, 12, 13, 4, 20, 21, 23, 24, 30, 31, 32, 34, 40, 41, 42, 43)
∴ n(S) = 16
i) Probability of getting the number formed is greater than 42
= No. of possible outcomes/Total outcomes
here no. of possible outcomes = 1 (that is 43 only)
∴ Probability = 1/16 ______ (1)
ii) In the sample space multiples of ‘4’ = 12, 20, 24, 32, 40
∴ No. of multiples of 4 = 5
Now probability for forming a multiple of ’4’ = 5/16 _____ (2)
Question 13.
A box contains 1 to 100 number cards. If one card is drawn at random. Find the probability of that card will be
i) a perfect square
ii) a prime number
iii) a two digit number
iv) a multiple of 9.
Solution:
Total number of possible outcomes = n(S) = 100
i) Let ‘E’ be an event of getting a perfect square.
Favourable outcomes to E = {1, 4, 9, 16, 25, 36, 49, 64, 81, 100}
n(E) = 10.
∴ P(E) = n(E)/n(S) = 10/100 = 1/10
ii) Let ‘F’ be an event of getting a prime number.
Favourable outcomes to
F = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97}
n(F) = 25. ∴ P(F) = n(F)/n(S) = 25/100 = 1/4
iii) Let ‘G’ be an event of getting a two digit number.
Favourable outcomes to G = {10 to 99}
n(G) = 90. ∴ P(G) = n(G)/n(S) = 90/100 = 9/10
iv) Let ‘H’ be an event of getting a multiple of 9.
Favourable outcomes to
H = {9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99}
n(H) = 11.
∴ P(H) = n(H)/n(S) = 11/100
Question 14.
A dice is thrown twice. What is the probability that
i) 3 will come up at least once ?
ii) 3 will not come up either time ?
Solution:
When a dice is thrown once sample space = S = (1, 2, 3, 4, 5, 6}
Total number of outcomes = n(S) = 6
A dice thrown twice, then total number of outcomes = n(S) = 6 × 6 = 36
i) Let ‘E’ be an event of getting 3 will come up at least once.
Favourable outcomes to E = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (1, 3), (2, 3), (4, 3), (5, 3), (6, 3)}
n(E) = 11
∴ P(E) = n(E)/n(S) = 11/36
ii) Probability that 3 will not come up either time = F = 36 - 11 = 25
Question 15.
One card is drawn from a well - shuffled deck of 52 cards. Find the probability of getting
(i) a king of black colour
(ii) a face card
(iii) a spade
(iv) a card not a heart
Solution:
When one card is drawn from a well shuffled deck of 52 cards.
The total number of outcomes in sample space is n(S) = 52
Probability = No.of favourable outcomes/Total No.of outcomes
Event i) : Consider E1 be the Event of getting a king of black colour.
Number of favourable outcomes for the event E1 is n(E1) = 2
P(E1) = n(E1)/n(S) = 2/52 = 1/26.
Event ii) : Consider E2 be the Event of getting a face card.
Number of favourable outcomes for the event E2 is n(E2) = 12
P(E2) = n(E2)/n(S) = 12/52 = 3/13.
Event iii) : Consider E3 be the Event of getting a spade.
Number of favourable outcomes for the event E3 is n(E3) = 13
P(E3) = n(E3)/n(S) = 13/52 = 1/4.
Event iv) : Consider E4 be the Event of getting a card not to be a heart.
Number of favourable outcomes for the event E4 is n(E4) = 39
P(E4) = n(E4)/n(S) = 39/52 = 3/4.
Question 16.
One card is drawn from a well shuffled deck of 52 cards. Find the probability of getting:
i) A queen of black colour
ii) a face card
iii) a jack of diamond
iv) a club card
Solution:
Total number of cards in a deck n(S) = 52
i) Probability of getting "A queen of black colour".
Number of favourable outcomes for getting a queen of black colour.
n(Q) = 2
∴ P(Q) = Number of favourable outcomes/Total Number of all possible outcomes
∴ P(Q) = 2/52 = 1/26
ii) Probability of getting "a face card". Number of favourable for getting face card = 12
∴ P(F) = 12/52 = 3/13
iii) Probability of getting "a jack of diamond".
Number of favourable outcomes for getting a jack of diamond = 1
∴ P(J) = 1/52
iv) Probability of getting a club card. Number of favourable outcomes for getting a club card = 13
∴ P(C) = 13/52 = 1/4
Question 17.
One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting:
i) A face card of diamond
ii) Ace card
iii) Spade card
iv) A jack of red
Solution:
Total number of cards in a deck = 52.
∴ Number of all possible outcomes n(S) = 52
i) Number of outcomes favourable to the face card of diamond n(D) = 3
∴ Probability of getting face card of diamond
P(D) = No.of favourable outcomes/No.of total outcomes
= n(D)/n(S) = 3/52
ii) Number of outcomes favourable to ace card n(A) = 4
∴ P(A) = n(A)/n(S) = 4/52 = 1/13
iii) Number of outcomes favourable to spade card n(SP) = 13
∴ P(SP) = 13/52 = 1/4
iv) Number of outcomes favourable to jack of red n(JR) = 2
∴ P(JR) = 2/52 = 1/26