12th Lesson Surface Areas and Volumes Class 10 Important Questions with Solutions
10th Class Maths Surface Areas and Volumes 1 Mark Important Questions
Question 1.
If the radii of two spheres are in the ratio 2 : 3, then find the ratio of their respective volumes.
Solution:
r1 : r2 = 2 : 3
V1 : V2 = 2/3 πr23 : 2/3 r23
r13 : r23
23 : 33
8 : 27
Given that, Area of base (πr2) = 156
Vertical height of cone (h) = 8 cm
Question 2.
Find the volume of a right circular cone whose area of the base is 156 cm2 and the vertical height is 8 cm.
Solution:
V = 1/3 πr2h = 1/3 × 156 × 8
= 52 × 8
= 416 cm2
Question 3.
Find the total surface area of a solid hemisphere of radius 7 cm.
Solution:
r = 7 cm
TSA of hemisphere = 3πr2
= 3 × 22/7 × 7 × 7 cm2
= 66 × 7 cm2
= 462 cm2
(or) TSA of hemisphere = 3πr2
= 3 × π × 7 × 7
= 147π cm2
Question 4.
The curved surface area of a right circular cylinder of height 14cm is 88 cm2. Find the diameter of its circular base.
Solution:
Cylinder, h = 14 cm
CSA = 88 cm2
2πrh = 88
2 × 22/7 × r × 14 = 88
44 × r × 2 = 88
r = 1
2r = 2 × 1
r = 1
d = 2r
d = 2 cm
Question 5.
A solid is of the form of a cone of radius V surmounted on a hemisphere of the same radius. If the height of the cone Is the same as the diameter of Its base, then find the volume of the solid.
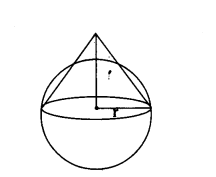
Solution:
Volume of solid = Vcone + Vhemisphere
= 1/3 πr2h + 23πr3
= 1/3 πr2[h + 2r]
= 1/3 πr2(r + 2r)(∴ h = r)
= 1/3 πr2 × 3r
= πr3
Question 6.
Assertion (A) : The surface area of largest sphere that can be inscribed in a hollow cube of side ‘a’ cm is πa2 cm2.
Reason (R) : The surface area of a sphere of radius ‘r’ is 4/3 πr3.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of the Assertion (A).
C) Assertion (A) is true, but Reason (R) is false.
D) Assertion (A) is false, but Reason (R) is true.
Solution:
C) Assertion (A) is true, but Reason (R) is false.
A : side of cube = a
radii of sphere = a/2
surface area = 4πr2
= 4π(a/2)2
= 4πa2/4
= πa2
A is true.
R : Surface area of sphere = 4 × πr2 R is wrong.
Question 7.
The curved surface area of a cylinder is 264 m2 and its volume is 924 m2. Then find the ratio of height to its diameter.
Solution:
Cylinder : 2πrh = 264
πr2h = 924
πr2h/2πrh = 924/264
r/2 = 924/264
r = 924/132
r = 7
d = 2 × 7 = 14 cm
2 × 22/7 × 7 × h = 264
h = 264/44
h = 6
h : d = 6 : 14 = 3 : 7
Question 8.
A rectangular sheet of paper 40 cm × 22 cm is rolled to form a hollow cylinder of height 40 tin then find the radius of cylinder.
Solution:
Rectangle: P = 2(l + b)
P = 2(40 + 22)
P = 2(62)
P = 124 m
Cylinder, h = 40 cm
2πrh = 124
2 × 22/7 × r × 40 = 124
r × 40 = 124 × 7/22 × 1/2
r = 62 × 7/22 × 1/40
r = 31×7/11×40 = 217/440
Question 9.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere ?
Solution:
2/3 πr3 =2πr2
r/3 = 1
r = 3
d = 2 × 3
d = 6
Question 10.
Diagonal of a cuboid is .....
Answer:
√l2+b2+h2
Question 11.
Volumes of two spheres are in the ratio 64 : 27 find the ratio of their surface areas.
Solution:
4/3 πr13 : 4/323 = 64 : 27
r13 : r23 = 43 : 33
r1 : r2 = 4 : 3
4πr12 : 4π22
42 : 32
16 : 9
Question 12.
A cylinder, a cone and a hemisphere have same base and same height, then the ratio of their volumes = ........
Solution:
Vcylinder : Vcone : Vhemisphere
πr2h : 1/3 πr2h : 2/3 πr3
πr3 : 1/3 πr3h : 2/3 πr3 (∵ r = h)
1 : 1/3 : 2/3
3 : 1 : 2
Question 13.
In a cone, l2 = .....
Answer:
h2 + r2
Question 14.
In a cone l2 - h2 = .......
Answer:
r2
Question 15.
Foot ball is an example of .......
Answer:
Sphere
Question 16.
Vertical cross section of cylinder is ......
A) Square
B) Circle
C) Semi circle
D) Rectangle
Answer:
D) Rectangle
Question 17.
The edge of a cube is 12 cm then its volume is ..... cm3.
Solution:
V = 123 = 1728 cm3
Question 18.
The volume of cube is 125 cm3 then its edge is ....... cm.
Answer:
5
Question 19.
Joker’s cap is an example of .......
A) Cuboid
B) Semi circle
C) Sphere
D) Cone
Solution:
D) Cone
Question 20.
Heap of stones is an example of .......
A) Cone
B) Cylinder
C) Circle
D) None
Answer:
A) Cone
Question 21.
Volume of cone = ..... x Volume of cylinder.
Answer:
1/3
Question 22.
Stem of a tree is an example of .......
A) Sphere
B) Cone
C) Cylinder
D) Rectangle
Answer:
C) Cylinder
Question 23.
Diagonal of a cube of edge ‘a’ units is ......
Solution:
a√3
Question 24.
The volume of a right circular cylinder of base radius 7 cm and height 10 cm is ..... cm3.
Solution:
r = 7 cm
h = 10 cm
V = πr2h
= 22/7 × 7 × 7 × 10
= 1540 cm3
Question 25.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3 then the ratio of their volumes =........
r1 : r2 = 2 : 3
h1 : h2 = 5 : 3
πr12h1 : πr22h2
22 × 5 : 32 × 3
20 : 27
Question 26.
The radius (r) of a sphere is reduced to its half then new volume would be ........
Solution:
Let radius = r/2
V = r/2 π(r/2)3 = 4/3π

Question 29.
The total surface area of sphere is 98.56 cm2 then the radius of the sphere is ....... cm.
Solution:
4πr2 = 98.56
r2 = 98.56×7/4×22
r2 = 7.84
r = 2.8 cm
Question 30.
What is the volume nearly equal to a metallic spherical ball of radius 4.5 cm?
Solution:
V = 4/3 πr3 ⇒ V = 4/3 × 22/7 × 4.5 × 4.5 × 4.5
V = 382 cm3
Question 31.
If the volume and surface area of a sphere is numerically equal, then its radius is ...... units.
Solution:
4πr3 = 4/3 πr3 ⇒ 1 = 1/3 × r
r = 3 units
Question 32.
The surface area of sphere of radius 10.5 cm is ....... cm2.
Solution:
Surface area = 4πr2
= 4 × 22/7 × 10.5 × 10.5 cm2
= 1386 cm2
Question 33.
The surface area of asphere of diameter 3.5 cm is ....... cm2.
Solution:
r = 3.5/2 cm
Surface area of sphere = 4πr2
4 × 22/7 × 3.5/2 × 3.5/2
= 38.5 cm2
Question 34.
The surface area of a sphere is 154 cm2 then its radius is ...... cm.
Solution:
4πr2 = 154
4 × 22/7 × r2 = 154
r2 = 154×7/22×4
r2 = 12.25
r = 3.5 cm
Question 35.
In a cone, the diameter ofbase is 10.5 cm and slant height is 10 cm then its curved surface area is..... cm2.
Solution:
r = 10.5/2
l = 10 cm
CSA = πrl
= 22/7 × 10.5/2 × 10
= 165 cm2
Question 36.
When two cubes are joined together the resultant figure is
A) Cone
B) Cuboid
C) Cube
D) Cylinder
Answer:
B) Cuboid
Question 37.
TSA of cone = .........
Answer:
πr (l + t)
Question 38.
Curved surface area of a hemisphere is 308 cm2 then its total surface area is..... cm2.
Solution:
2πr2 = 308
2 × 22/7 × r2 = 308
r2 = 308 × 7/22 × 1/2
r2 = 49
r = 7 cm
TSA = 3πr2
= 3 × 22/7 × 7 × 7
= 66 × 7
= 462 cm2
Question 39.
Write the area of four walls of a room.
Answer:
2h (l + b)
Question 40.
Two cubes of edge 6 cm are joined end to end. Then the resulting cuboid has the total surface area ...... cm2.
A) 160
B) 360
C) 240
D) None
Solution:
B) 360
l = 6 + 6 = 12 cm
b = 6 cm
h = 6 cm
TSA = 2(lb + bh + lh)
= 2(180)
= 360 cm2
Question 41.
Assertion (A) : The volume of a cube of edge 1 cm is 2 cm3.
Reason (R) : Volume of a cube is a3
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) istrue.
Answer:
D) Assertion (A) is false but reason (R) istrue.
Question 42.
Assertion (A) : Area of four walls of a room is 2h(l + b).
Reason (R) : CSA of cone = πrl.
A) Both assertion (A) and Treason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Question 43.
Assertion (A): Volume of cylinder = πr2h.
Reason (R) : A cube has 6 faces. .
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Question 44.
Assertion (A) : Volume of hemisphere of radius 7 cm is 616/3 cm2.
Reason (R): Volume of hemisphere = 2/3 πr3
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R)
Question 45.
Assertion (A) : CSA of cylinder with h = 7 cm, r = 10 cm is 440 cm2
Reason (R) : Volume of cube = a3
A) Both assertion (A) and reason (R) are true and reason (R) is the correct
explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
Question 46.
Assertion (A): The maximum length of a rod that can be placed in a room of dimensions 12 m × 11 m × 10 m is 13 m.
Reason (R) : Diagonal of a cuboid is √l2+b2+h2
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
D) Assertion (A) is false but reason (R) is true.
Question 47.
Assertion (A) : The volume of sphere of radius 5 cm is 4π cm3
Reason (R) : Volume of sphere = πr3.
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
D) Assertion (A) is false but reason (R) is true.
Question 48.
Assertion (A) : In a cone h = 4 cm r = 3 cm then l = 5 cm
Reason (R) : In a cone l2 = h2 + r2
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Question 49.
Assertion (A) : In a hemisphere if r = 10.5 cm then volume = 95.2 cm3
Reason (R): Volume of Hemisphere is 2/3 πr3
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
D) Assertion (A) is false but reason (R) is true.
Question 50.
Assertion (A) : The ratio of volume of two cubes is 1 : 27 then the ratio of their surface areas is 1 : 9
Reason (R) : Surface area of cube = 2h (l + b) - 2
A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
B) Both assertion (A) and reason (R) are true but reason (R:) is not the correct explanation of assertion (A).
C) Assertion (A) is true but reason (R) is false.
D) Assertion (A) is false but reason (R) is true.
Answer:
B) Both assertion (A) and reason (R) are true but reason (R:) is not the correct explanation of assertion (A).
Question 51.
The capacity of an oil drum is 10 litres then what is its volume ? ?(in cm3)
Answer:
10,000 cm3
Question 52.
Food grains are to be stored in containers of the same base length and height. Which type of containers are required less in number to store a fixed quantity of grains ?
i) Right Circular Cylinder
ii) Cube
iii) Right Circular Cone
Answer:
ii) Cube
Question 53.
Choose the correct answer satisfying the following statements.
Statement (A) : The ratio of volumes of cone and cylinder of same base and same height is 3 : 1 Statement (B) : Hie ratio of volumes of sphere and cone of same radius and same height is 2 : 1
i) Both A and B are true
ii) A is true, B is false
iii) A is false, B is true
iv) Both A and B are false
Answer:
iv) Both A and Bare false
Question 54.
Find the volume of a cylinder whose base radius is 3 cm and height is 7 cm.
Solution:
Radius of a cylinder r = 3 cm.
Height h = 7 cm.
Volume of the cylinder = πr2h
= 22/7 × (3)2 × 7
= 22/7 × 9 × 7
= 198 cm3
Question 55.
Curved surface area of Cone is πrl where l stands __________ .
Answer:
l = Slant height
Question 56.
The volume of a cube whose edge is 6 cm is
A) 108 cm3
B) 18 cm3
C) 216 cm3
D) 144 cm3
Answer:
C) 216 cm3
Question 57.
Find the volume of a cube, whose side is 4 cm.
Solution:
Side = a = 4 cm
Volume of cube V = a3 = 43 = 64 cm3
Question 58.
Find the volume of a sphere of radius 21 cm. (Take π = 22/7)
Solution:
Volume of the sphere = 4/3 πr3
= 4/3 × 22/7 × 21 × 21 × 21
= 38, 808 (cm)3
Question 59.
Find the total surface area of a hemisphere, whose radius is 7 cm.
Solution:
Radius of Hemisphere, r = 7 cm
T.S.A of Hemisphere = 3πr2
= 3 × 22/7 × 7 × 7
= 462 (cm)2
Question 60.
Find the volume of right circular cone with radius 3 cm. and height 14 cm.
Solution:
Volume of right circular cone = 1/3 πr2 h
= 1/3 × 22/7 × 3 × 3 × 14
= 132 cm2
10th Class Maths Surface Areas and Volumes 2 Mark Important Questions
Question 1.
From a solid right circular cylinder of height 14 cm and base radius 6 cm, a right circular cone of same height and same base radius is removed. Find the volume of the remaining solid.
Solution:
In a cylinder,
height, h = 14 cm
radius, r = 6 cm
In a case, h = 14 cm
r = 6 cm
Volume of remaining solid
= Vcylinder - Vcone
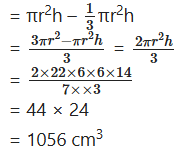
Question 2.
Find the curved surface area of a right circular cone whose height is 15 cm and base radius is 8 cm.
[Use π = 22/7]
Solution:
In a cone, height, h = 15 cm
radius, h = 8 cm
l = h2 + r2
= 152 + 82
= 225 + 64
l2 = 289
l = √289
l = 17 cm
CSA = πrl = 22/7 × 8 × 7 cm2
= 2992/7 cm2
Question 3.
The surface area of a sphere is 616 sq cm. Find its radius. [Use π = 22/7]
Solution:
Surface area of sphere = 616 cm2
4πr2 = 616
4 × 22/7 × r2 = 616
r2 = 616 × 7/20 × 1/4
r2 = 49
r = 7 cm
∴ Radius of sphere = 7 cm
Question 4.
Three cubes each of volume 64 cm3 are joined end to end to form a cuboid. Find the total surface area of the cuboid so formed ?
Solution:
Volume of cube = 64 cm3
a3 = 64
a3 = 43
a = 4 cm
When 3 cubes are joined together cuboid is formed.
l = 4 + 4 + 4 = 12 cm
b = 4 cm
h = 4 cm
Total surface area = 2(lb + bh + lh)
= 2(12 × 4 + 4 × 4 + 12 × 4)
= 2(481 + 6 + 48)
= 2(112) cm2
= 224 cm2
Question 5.
The volume of a right circular cylinder with its height equal to the radius is 25 1/7
cm3. Find the height of the cylinder. (Use π = 22/7)
Solution:
In a cylinder, r = h.
Volume of cylinder = πr2h
25 1/7 = πr3 ⇒ 176/7 = 22/7 r3
8 = r3
r3 = 23
r = 2 cm
∴ height h = 2 cm
Question 6.
A cubical block of side 7 cm is surmounted by a hemisphere of largest possible diameter as shown in Figure. Find the total surface area of the solid.
Solution:
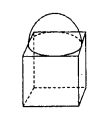
Side of cube = 7 cm
radius of hemisphere = 7/2 cm
Total surface area of solid
= TSA of cube + Surface area of hemisphere - Area of circle
= 6a2 + 2πr2 - πr2
= 6(7)2 + πr2
= 294 + 22/7 × 7/2 × 7/2
= 294 + 77/2 cm2
= 294 + 38.5 cm2
= 332.5 cm2
Question 7.
A sphere of diameter 6 cm is dropped in a right circular cylindrical vessel partly filled with water. The dimater of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Solution:
Let the water level raised in cylindrical vessel be h cm
Vsphere = Vwater displaced in cylinder
4πr3/3 = πR2h
4/3 π(3)3 = π(6)2h
4/3 × 27 = 36 h
h = 36/36
h = 1 cm
Question 8.
A cylinder and a cone have base radii 5 cm and 3 cm respectively and their respective heights are 4 cm and 8 cm. Find the ratio of their volumes.
Solution:
Cone
r = 3 cm
h = 8 cm
Volume = 1/3 πr2h
= 1/3 × 22/7 × 3 × 3 × 8
Cylinder
r = 5 cm
h = 4 cm
Volume = πr2h
= 22/7 × 5 × 5 × 4
Ratio = 22/7 × 3 × 8 : 22/7 × 5 × 5 × 4
= 3 × 8 : 5 × 5 × 4 = 6 : 25
Question 9.
A sphere of maximum volume is cut from a solid hemisphere of radius 6 cm. Find the volume of the cut out sphere.
Solution:
In Hemisphere, r = 6 cm
radius of sphere, R = 6/2 = 3 cm
Volume of sphere = 4/3 πR3
= 4/3 × 22/7 × 3
= 4/3 × 9 = 729/7
= 113.14 cm3
Question 10.
Two cubes of 5 cm each are kept together joining edge to edge to form a cuboid. Find the surface area of cuboid so formed.
Solution:
Two cubes of each edge 5 cm are joined then it is a cuboid
l = 5 + 5 = 10 cm
b = 5 cm
c = 5 cm
Surface of cuboid = 2(lb + bh + lh)
= 2[ 10 × 5 + 5 × 5 + 10 × 5]
= 2[50 + 25 + 50]
= 2(125) cm2
= 250 cm2
Question 11.
If the total surface area of a solid hemisphere is 462 cm2, find its volume [Take π = 22/7]
Solution:
Total surface area of hemisphere = 462 cm2
3πr2 = 462
3 × 22/7 × r2 = 462
r2 = 462 × 7/22 × 1/3
r2 = 21 × 7 × 1/3
r2 = 7 × 7
r = 7 cm
Volume = 2/3 πr3
= 2/3 × 2/3 × 2156/3 cm3
Question 12.
A 5m wide cloth is used to make a conical tent of base diameter 14m and height 24m. Find the cost of cloth used at the rate of ₹ 25 per metre.
Solution:
In a cone, h = 24 m
d = 14 m
r = 14/2 = 7 m
l2 = h2 + r2
l2 = 242 + 72
l2 = 576 + 49
l2 = 625
l = √625
l = 25 m
CSA of cone = πrl
= 22/7 × 7 × 25 cm2
= 550 m2
Length of cloth used = Area/width of cloth = 550/5 - 110 m
Cost of cloth = ₹ 25 per m.
Total cost = ₹ 25 × 110
= ₹ 2750
Question 13.
A conical tent is 10m high and the radius of its base is 24m. Find the cost of cloth used to make the tent at ₹ 70/m3.
Solution:
In a cone, h = 10 m
r = 24 m
CSA = πrl
l = √h2+r2
= π × 24 × √102+242
= 22/7 × 24 × √676
= 22/7 × 24 × 26 m2
Cost = ₹ 70 × 22/7 × 24 × 26
= ₹ 137280
Question 14.
From a solid cylinder whose height is 2.4 cm and diameter 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the volume of the remaining solid to the nearest cm3 (Use π = 22/7)
Solution:
Height of cone = height of cylinder, h = 2.4 cm
Diameter of cylindrical part = 1.4 cm
r = 1.4/2 = 0.7cm
Slant heigth (l) = √h2+r2
= √(2.4)2+(0.7)2
= √5.76+0.49
= √6.25
= 2.5 cm
Total surface area of remaining solid
= CSA of cylindrical part + CSA of conical part + Area of cylindrical base
= 2πrh + πrl + πr2
= 2 × 22/7 × 0.7 × 2.4 × 22/7 × 0.7 × 2.5 + 22/7 × 0.7 × 0.7 cm2
= 4.4 × 2.4 + 2.2 × 2 + 2.2 × 0.7
= 10.56 + 5.50 + 1.54
= 17.60 cm2
∴ TSA of remaining solid in nearest to 18 cm2.
Question 15.
The circumference of the base of a 9 in high wooden solid cone is 44 m. Find the volume of the cone.
Solution:
Let r be the radius
h = 9 m
Circumference of base = 2πr = 44 m
2 × 22/7 × r = 44
r = 44 × 7/22 × 1/2
r = 7 m
Volume of cone = 1/3 πr2h
= 1/3 × 22/7 × 7 × 7 × 9
= 22 × 21 m2
= 462 m3
Question 16.
Find the number of coins of 1.5 cm in diameter and 0.2 cm thick to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:
Let n be the number of cones required Volume of cylinder = n × Volume of 1.5 cm diameter coin
πR2H = n × πr2h ⇒ n = R2H/r2h
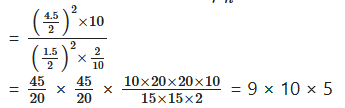
n = 450.
∴ number of coins required = 450.
Question 17.
A glass cylinder with diameter 20 cm has water to a height of 9 cm. A metal cube of 8 cm edge is immersed in it completely. Calculate the height by which water will rise in the cylinder. [Use π = 3.14]
Solution:
Let the water rise be h cm
Volume of water displaced = Volume of the cube of edge 8 cm
πr2h = 83
3.14 × 102 × h = 8 × 8 × 8
h = 8×8×8/3.14×10×10
h = 512/314 ⇒ h = 1.6 cm
∴ height = 1.6 cm
Question 18.
In a construction of kitchen shed at school, a truck unloaded the sand which was formed in the shape of a cone. The base radius of the cone is 2.7 m. and its height is 7 m. Find the volume of sand unloaded there.
Solution:
Base radius of the cone (r) = 2.7 m
height (h) = 7 m.
Volume of the cone = 1/3 pr2h
= 1/3 × 22/7 × (2.7)2 × 7
= 1/3 × 22/7 × 2.7 × 2.7 × 7
∴ Volume of the sand = 53.46 m3.
10th Class Maths Surface Areas and Volumes 4 Mark Important Questions
Question 1.
Find the number of spherical lead shots, each of diameter 6 cm that can be made from a splid cuboid of lead having dimensions 24 cm × 22 cm × 12 cm.
Solution:
In a cuboid l = 24 cm
b = 22 cm
h = 12 cm
Spherical shot, d = 6 cm
r = 6/2 = 3 cm

Question 2.
A wooden souvenir is made by scooping out a hemisphere from each end of a solid cylinder. If the height of the cylinder is 10 cm and its base is of radius 3.5 cm then find the total cost of polishing the souvenir at the rate of Rs. 10 per cm2.
Solution:
In cylinder, h = 10 cm
r = 3.5 cm
TSA of the article = CSA of cylinder + 2
surface area of hemisphere
= 2πrh + 2(2πr2)
= 2πr (h + 2r)
= 2 × 22/7 × 3.5(10 + 2(3.5))cm2
= 2 × 22 × 0.5 (10 + 7) cm2
= 22(17)
= 374 cm2
Cost of polishing = ₹ 10 per cm2
Total cost = 374 × ₹ 10
= ₹ 3740
Question 3.
A right circular cone of radius 3 cm has a curved surface area of 47.1 cm2. Find the volume of the cone (Use π = 3.14)
Solution:
In a cone raius = 3 cm
surface area = 47.1 cm2
πrl = 47.1
3.14 × 3 × l = 47.1
l = 47.1/3.14×3
l = 15/3
l = 5 cm
Volume of cone = 1/3 πr2h
l2 = h2 + r2
52 = h2 + 32
25 - 9 = h2
h2 = 16
h = 4 cm
Volume = 1/3 × 3.14 × 3 × 3 × 4 cm3
= 3.14 × 12 cm3
= 37.68 cm3
Question 4.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq.cm. Find the volume of the cylinder (Use π = 22/7)
Solution:
In a cone,
r + h = 37
TSA = 16.28 cm2
2πr(h + r) = 1628
2 × 22/7 × r × 37 = 1628
r = 1628 × 7/22 × 1/37 × 1/2
22 37 2
r = 7 cm
h = 37 - 7 = 30 cm
Circumference = 2πr = 2 × 22/7 × 7 = 44 cm
Volume of cylinder = πr2h
= 22/7 × 7 × 7 × 30m3
= 22 × 210 cm3
= 4620 cm3
Question 5.
In the given figure, a tent is in the shape of a cylinder surmounted by a conical top of same diameter. If the height and diameter of cylindrical part are 2.1 m and 3m respectively and the slant height of conical part is 2.8m. Find the cost of canvas needed to make the tent if the canvas available at the rate of ₹ 500 per sq. (Use π = 22/7)
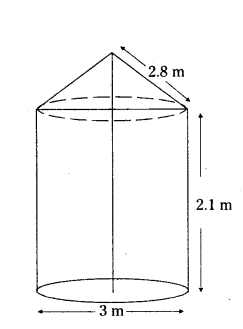
Solution:
radius of cone = radius of cylinder
r = 3/2 m
Slant height, l = 2.8 m
Height of cylinder, h = 2.1 m ,
Canvas needed to make the tent = CSA of conical part + CSA of cylindrical part
= πrl + 2πrh = 22/7 × 3/2 × 2.8 + 2 × 22/7 × 3/2 × 2.1
= 13.2 + 19.8 = 33 m2
Cost of 1 m2 canvas = ₹ 500
Cost of 33 m2 convas = 33 × 500
= ₹ 16,500
∴ Cost to make the tent = 116,500
Question 6.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the
hemisphere can have ? Find the cost of painting the total surface area of the solid so formed, at the rate of ₹ 5 per 100 sq. cm. (Use ₹ = 3.14)
Solution:
Total surface area of the solid = TSA of cube + CSA of hemisphere - Area of base of hemisphere
= 6a2 + 2πr2 - πr2
= 6 × 102 + 2 × 3.14 × 52 - 314 × 52cm2
= 600 + 157 - 78.5
= 678.5 cm2
Cost of painting = 5 per 100 cm2
Cost of painting the solid
= 678.5 × 5/100
= ₹ 33.925
Question 7.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of some radius on its circular face. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:
Total surface area of toy = CSA of cone + Surface area of hemisphere
= πrl + 2πr2
In a cone, r = 3.5 cm,
h = 15.5 - 3.5 = 12 cm
l2 - h2 + r2
l2 = 122 + 3.52
l2 = 144 + 12.25
l2 = 156.25
l = √156.25
l = 12.5
Question 8.
A hemispherical bowl of internal diameter 36 cm contains liquid. This liquid is filled into 72 cylindrical bottles of dimeter 6 cm. Find the height of each bottle, if 10% liquid is wasted in this transfer.
Solution:
In hemisphere
Diameter, d = 36 cm
radius, r = 18 cm
Volume of spherical bowl = 2/3 πr3
= 2/3 × 22/7 × 18 × 18 × 18
= 12219.43 cm3
In cylinder,
r = 3 cm
Volume = πr2h
Volume of 72 bottles = 22/7 × 3 × 3 × h × 72
Now 10% of 12219.43 = 1221.943 cm3 is wasted.
Remaining volume
= 12219.43 - 1221.943 cm3
= 10997.487 cm3
72 × 22/7 × 3 × 3 × h = 10997.487
h = 10997.487×7/72×22×9
height, h = 5.4 cm
Question 9.
A hemispherical bowl of internal diameter 30 cm contains some liquid. This liquid is to be filled into cylindrical shaped bottles each of diameter 5 cm and height 6 cm. Find the number of bottles necessary to empty the bowl.
Solution:
Inner diameter of bowl = 30 cm
Inner radius of bowl = 15 cm
Volume of liquid = 2/3 πr3
= 2/3 × π × 15 × 15 × 15 cm3
Radius of each cylindrical bottle = 2.5 cm
h = 6 cm
Volume of each cylindrical bottle
= πr2h
= π × 5/2 × 5/2 × 6 cm3
= 25/4 × 6π
Required number of bottles
= 2/3×π×15×15×15/25/2×π = 60
Question 10.
The rain water from 22 m × 20 m roof drains into cylindrical vessel of diameter 2 m and height 3.5 m. If the rain water collected from the roof fills 4/5 th of cylindrical vessel then find the rainfall in cm.
Solution:
Length of the roof = 22 m
Breadth of the roof = 20 m
Let the height of water on the roof be h m
Radius of cylinderical vessel = r = 2/2 = 1m
Height of water in the cylindrical vessel H = 3.5 m
Volume of water falling on the roof = Volume of water in the cylinder
lbh = πr2h
22 × 20 × h = π × 72 × 3.5
h = 22/7 × 1×35/22×20
h = 1/40 m
h = 2.5 cm
∴ 2.5 cm of rainfall falls on the roof.
Question 11.
A hollow cylindrical pipe is made up of copper. It is 21 m long, the outer and inner diameters of the pipe are 10 cm and 6 cm respectively. Find the volume of the copper used in making the pipe.
Solution:
Height of cylindrical pipe, h = 21 m = 210 cm
External Radius, R = 10/2 = 5 cm
Internal Radius, r = 6/2 = 3cm
Volume of copper making the pipe
= πR2h - πr2h
= πh(R2 - r2)
= 22/7 × 210(52 - 32)
= 22/7 × 210(25 - 9)
= 22 × 30 × 16
= 10560 cm3
Question 12.
A glass is in the shape of a cylinder of radius 7 cm and height 10 cm. Find the volume of juice in litre required to fill 6 such glasses. (Use π = 22/7)
Solution:
radius = 7 cm
height =10 cm
volume of 1 gram = πr2h
= 22/7 × 7 × 7 × 10cm3
= 22 × 70 cm3
= 1,540 cm3
∴ Volume of 6 such glasses = 1540 × 6 = 9,240 cm3
Question 13.
The radii of two cylinder are in the ratio of 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their curved surface area.
Solution:
In two cylinders
Ratio in radii of two cylinder = 2 : 3
Ratio of their heights = 5 : 3
r1 : r2 = 2 : 3
h1 : h2 = 5 : 3
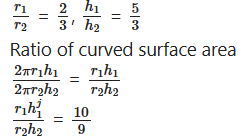
∴ Required Ratio = 10 : 9.
Question 14.
A wooden toy was made by scooping at a hemisphere of same radius from each end of a solid cylinder. If the length of the cylinder is 10 cm, then find the volume of that toy.
Solution:
Radius of cylinder = Radius of hemisphere = r = 3.5 cm
height of the cylinder = h = 10 cm
Volume of the toy = Volume of the cylinder - Volume of two hemisphere
= πr2h - 2 × 2/3 πr3 = πr2 (h - 4r/3)
= πr2 (10 - 4×3.5/3) = πr2 (10 - 14/3)
= 22/7 × 3.5 × 3.5 × 16/3
= 616/3 cm3
= 205.333 cm3
Question 15.
The base area of a cone is 616 sq.cm and its height is 48 cm. Find its total surface area.
Solution:
The base area of a cone = πr2 = 616 cm2
Given height of cone = 48 cm = h
Now π2 = 616
⇒ 22/7 × r2 = 616
⇒ r2 = 616×7/22
= 7 × 4 × 7
⇒ r = √7×4×7<
= 7 × 2
= 14 cm
If r = 14, h = 48, then
Slant height (l) = √r2+h2
= √142+482
= √196+2304
= √2500
= 50 cm.
∴ Curved surface area of the cone
= πrl = 22/7 × 14 × 50 = 2200
∴ Total surface area
= C.S.A + base area
= 2200 + 616 = 2816 cm2
10th Class Maths Surface Areas and Volumes 8 Mark Important Questions
Question 1.
The diameter of a metallic sphere is 6 cm. The sphere is melted and drawn into a wire of uniform cross-section. If the length of the wire is 36 m, And its radius.
Solution:
Given diameter of sphere = 6 cm
Radius of the sphere r = 6/2 = 3 cm
length of wire h = 36 m = 3600 cm
Volume of sphere V = 4/3 πr3
= 4/3 π × 3 × 3 ⇒ V = 36π cm3
but, given sphere is melted and drawn into a uniform wire. Wire Is in the shape of cylinder.
So, volume of wire = volume of sphere.
πr2h = 36π
π × r2 × 3600 = 36π
r2 = 36π/π×3600 = 1/100 = (1/10)2
r = 1/10 = 0.1 cm = 1 mm
Therefore radius of wire = 0.1 cm/1 mm
Question 2.
A metallic sphere of radius 4.2 cm is melted and recast into the shape of cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
Given radius of the sphere r = 4.2 cm
radius of the cylinder = 6 cm
height of the cylinder = ?
metallic sphere is recast into cylinder.
So, volume of cylinder = volume of sphere
πr2h = 4/3 πr3
π . 6 × 6 × h = 4/3 π × 4.2 × 4.2 × 4.2
h = 4/3 × π×4.2×4.2×4.2/π×6×6
= 4 × 1.4 × 0.7 × 0.7 = 2.774 cm
Therefore, height of the cylinder = 2.774 cm.
Question 3.
A sphere of diameter 6 cm is dropped in a right circular cylinderical vessel pastly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Solution:
Given diameter of sphere = 6 cm
radius = d/2 = 6/2 = 3 cm
diameter of the cylinder = 12 cm
radius = d/2 = 6 cm
Volume of sphere = 4/3 πr3
= 4/3 π × 3 × 3 × 3
= 36π cm3
Volume of cylinder = πr2h
= π × 62 h cm3
But, Volume of cylinder = Volume of sphere
π × 36 × h = 36π
h = 36π/π36 = 1cm
Therefore, water level raised by 1 cm.
Question 4.
Solid cylinder of brass 8 m high and 4 m diameter is melted and recast into a cone of diameter 3 m, find the height of the cone.
Given radius of cylinder (r) = d/2 = 4/2 = 2 m
height of cylinder h = 8 m
radius of cone r = 3/2 m
Given volume of cone = volume of cylinder
1/3 πr
2h = πr
2h
1/3 × π × 3/2 3/2 × h = π × 2 × 2 × 8
h = π×2×2×8×3×2×2×2/π×3××3
Therefore, height of the cone
128/3 = 42.66 m
Question 5.
Find the number of coins, 1.5 cm in diameter and 0.2 cm thick to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:
Given coin is in the shape of cylinder
radius of coin = d/2 = 1.5/2 cm
Thickness of coin h = 0.2 cm
Volume of coin = πr2h
= π × 1.5/2 × 1.5/2 × 0.2 cm3
Radius of cylinder r = d/2 = 4.5/2 cm
height of cylinder h = 10 cm
Volume of cylinder = πr2h
= π × 4.5/2 × 4.5/2 × 10 cm3
Let number of coins = n
Coins are melted to form a cylinder.
So, n × volume of coin = volume of cylinder
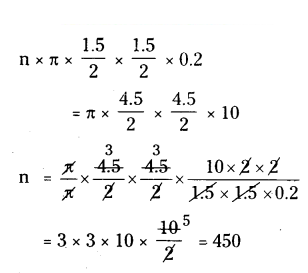
Therefore number of coins = 450
Question 6.
A 20 m deep well with diameter 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
Given diameter of the well d = 7 m
radius r = 7/2 m
height of the well h = 20 m
length of the platform l = 22 m
breadth b = 14 m
height h = ?
Volume of the earth in the platform = Volume of deep well
l.b.h = πr2h
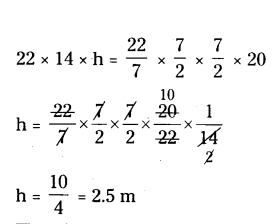
Therefore height of the platform = 2.5 m
Question 7.
A cylindrical pipe has inner diameter of 7 cm and water flows through it at 192.5 l per minute. Find the rate of flow in kilometres per hour.
Solution:
Given inner diameter of cylinder d = 7 cm
radius r = 7/2 cm
Volume of water per minute = 192.5 l.
Volume of water per hour
= (192.5 × 60)l
= (192.5 × 60 × 1000) cm3
Let height of the cylinder = h cm
Volume of the cylinder = Volume of water flows per hour
πr2h = 192.50 × 60 × 1000
22/7 × 7/2 × 7/2 × h = 192.50 × 60 × 1000
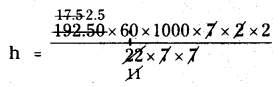
= 2.5 × 60 × 1000 × 2
h = 300000 cm = 3 km.
Therefore, the rate of flow of water is 3 km per hour.
Question 8.
A copper wire 3 mm in diameter is wound about a cylinder whose length is 1.2 m and diameter 10 cm, so as to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of the copper wire to be 8.88 gram per cm.
Solution:
Given diameter of the wire = d = 3 mm = 3/10 cm
Length of the wire (or) height of cylinder h = 1.2 m = 120 cm
Number of rounds taken by the wire in the cylinder = length of wire/diameter of wire
= 120/3/3/10 = 1200/3 = 400
Radius of the cylinder = d/2 = 10/2 cm
Circumference of wire per one round (or) length of wire per one round
= 2πr = 2 × 3.14 × 10/2
= 2 × 31.4 × 5 = 3.14 cm
Total length of wire used to make a cylinder =
length of wire per one round x number of rounds = 31.4 × 400 = 12560 cm
Given density of copper wire per cm = 8.88 grams
Mass of the wire
= length of wire × density of copper per cm
= 12560 × 8.88 = 111532.8 grams
Therefore total mass of the wire
= 111.533 kg.
Question 9.
How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid 11 cm × 10 cm × 7 cm ?
Solution:
Given radius of the coin (r) = d/2 = 1.75/2 cm
thickness or height of coin h = 2 mm = 2/10 cm
Volume of coin = πr2h
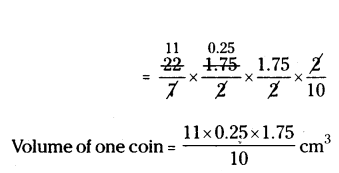
Let number of coins = n
Given coins are melted to form a cuboid dimensions of cuboid are 11 × 10 × 7
So, volume of x coins = volume of cuboid n × volume of coin = l.b.h
n × 11×0.25×1.75/10 = 11 × 10 × 7
n = ×11×10×7×10/×11×0.25×1.75
Therefore number of coins n = 1600
Question 10.
Water in a canal 1.5 m wide and 6 m deep in flow with speed of 10 km/ hour. How much area will it irrigate in 30 minutes if 8 cm of standing water is desired ?
Solution:
Given width of canal = 1.5 m
length of canal = 6 m
Area of the canal = 1.5 × 6 m2
Required area per 10 km/hour
= 1.5 × 6 × 10000
Required area per 10km/30minutes.
= 1.5 × 6 × 10000 × 1/2
Standing water = 8 cm (or) × 8/100 m
So, required area to irrigate = 1.5×6×10000×1/2/8/100
= 1.5×6×10000×100/8×2 m2
= 562500 m2
Question 11.
Cylindrical bucket 32 cm high and with radius of base 18 cm is filled with sand. This bucket is emptied out on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm. Find the radius and slant height of the heap.
Solution:
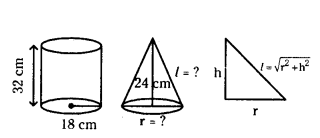
Given radius of cylinder r = 18 cm
height h = 32 cm
Volume of bucket = πr2h
= π × 18 × 18 × 32 cm3
Let radius of cone r = ?
height of cone h = 24 cm
Volume of cone = 1/3 πr2h
= 1/3 × π × r2 × 24
= 8πr2 cm3
We know that volume of cone = volume of cylinder
8πr2 = π × 18 × 18 × 32
r2 = π×18×18×32/8
r2 = 36 × 36 = 362
radius of the cone r = 36 cm
Slant height l = √r2+h2 = 362 + 242
= √1296+576
= √1872 = √13 cm
Question 12.
The surface area of solid metallic sphere is 616 cm2. It is melted and recast into a cone of height 28 cm. Find the diameter of the base of the cone so formed.
Solution:
Given surface area of sphere
4πr2 = 616 cm2
4 × 1/3 × r2 = 616
r2 = 616×7/4×22
r2 = 72
So, radius of sphere r = 7 cm
Sphere is melted into cone,
Given height of cone h = 28 cm
radius of cone r = ?
that is volume of cone = volue of sphere
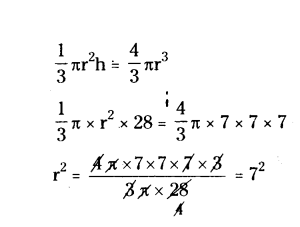
radius r = 7 cm
Diameter of cone = 2 × r = 2 × 7 = 14cm
Question 13.
A tent is in the form of a cylinder of diameter 20 m and height 2.5 m surmounted by a cone of equal base and height 7.5 m. Find the capacity of the tent and the cost of the canvas at Rs.100 per square metre.
Solution:
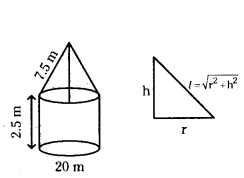
Given radius of the cylinder = d/2 = 20/2 = 10 m
height of the cylinder = 2.5 m
Volume of cylinder = πr2h
= π × 10 × 10 × 2.5 m3
radius of cone r = 10 m
height of cone h = 7.5 m
Volume of cone = 1/3 πr2h
= 1/3 × π × 10 × 10 × 7.5 m3
Capacity of tent = Volume of cylinder + Volume of cone
= π × 100 × 2.5 + 1/3 π × 100 × 7.5
= 100π (2.5 + 2.5)
Capacity of tent = 100 × 3.14 × 5 = 1570 m3
Surface area of cone = πrl
l = 12.5 m
πrl = π × 10 × 12.5 = 125π m2
Surface area of cylinder = 2πrh
= 2 × π × 10 × 2.5
= 50π m2
Total surface area of tent
= Surface area of cone + Surface area of cylinder
= 125π + 50π
= 175π m2
= 175 × 3.14
= 549.5 m2
Cost of canvas cloth of 100 per m2 is
= 549.5 × 100
= ₹ 54,950
AP 10th Class Maths Chapter 12 Important Questions Surface Areas and Volumes
Question 1.
Find the volume of a sphere of radius 21cm.(Take π = 22/7)
Solution:
Volume of the sphere = 4/3 πr3
= 4/3 × 22/7 × 21 × 21 × 21 = 38,808(cm)3
Question 2.
Find the total surface area of a hemisphere, whose radius is 7 cm.
Solution:
Radius of Hemisphere, r = 7 cm
T.S.A of Hemisphere = 3πr2
= 3 × 22/7 × 7 × 7 = 462 (cm)2
Question 3.
Find the volume of right circular cone with radius 3 cm. and height 14 cm.
Solution:
Volume of right circular cone = 1/3 πr2h
= 1/3 × 22/7 × 3 × 3 × 14 = 132 cm3
Question 4.
Find the curved surface area of cylinder, whose radius is 7 cm. and height is 10 cm.
Solution:
Radius of a cylinder = r = 7 cm
Height of a cylinder = h - 10 cm
CSA of a cylinder = A = 2πrh
= 2 × 22/7 × 7 × 10
= 44 × 10 = 440 sq.cm
Question 5.
The surface area of a football is 616 cm2, then find the radius of that ball. ( π = 22/7).
Solution:
Surface area of a football (sphere) = 4πr2.
4πr2 = 616
πr2 = 154
r2 = 154 × 7/22
r2 = 7 × 7 = 49
∴ r = 7 cm
Question 6.
The volume of a cylinder is 448π cm3 and height is 7 cm. What is its radius?
Solution:
Volume of the cylinder = πr2h = 448π
Here h = 7cm ,r = r
then πr2 × 7 = 448π
r2 = 448/7 = 64
∴ Radious (r) = 8 cm
Question 7.
Find the surface area of a sphere of radius 14 cm. (Take π = 22/7)
Solution:
Radius of given sphere = (r) = 14 cm
Formula for surface area of sphere = 4πr2
∴ Surface area of given sphere = 4 × 22/7 × 14 × 14 = 88 × 28 = 2464 cm2
Question 8.
Draw a rough diagram of a solid, showing the combination of a cone and cylinder, whose base radii are same.
Answer:
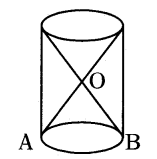
AB is radius of cylinder as well as cone.
Question 9.
Find the area of the paper sheet required to make a conical joker cap with radius 7 cm and slant height 14 cm.
Solution:
Given, radius = 7 cm
Slant height = 14 cm
Area of paper sheet = πrl
= 22/7 × 7 × 14
= 22 × 14 = 308 cm2
Question 10.
If the diameter of a sphere is equal to the side of a cube, find the ratio of their volumes.
Solution:
Let diameter of the sphere = d = side of the cube
∴ Radius of the sphere (r) = d/2
volume of the sphere = 4/3 πr3
= 4/3 π(d/2)3 = 4/3 π d3/8 = π/6 d3
And, volume of the cube = d3
∴ The ratio of volume of sphere to volume of cube = π/6 d3 : d3 = π/6 : 1
Question 11.
Find the volume and total surface area of a hemisphere whose radius is 35 cm?
Solution:
Radius of the hemisphere (r) = 35 cm.
Volume of the hemisphere = 2/3 πr3
= 2/3 × 22/7 × 35 × 35 × 35
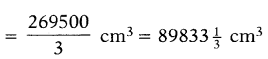
Total surface area = 3πr2
= 3 × 22/7 × 35 × 35 = 11550 cm2
Question 12.
A solid iron rod has a cylindrical shape. Its height is 11 cm and base diameter is 7 cm. Then find the total volume of 50 rods.
Solution:
The height of the cylinderical
Rod (h) = 11 cm,
Raidus (r) = 7/2 cm
Volume = πr2h = 22/7 × 7/2 × 7/2 × 11
= 423.5 (cm)3
Volume of 50 rods = 50 × 423.5 = 21175 (cm)3
Question 13.
Two cubes each of volume 125 cm3 are joined end to end together. Find the total surface area of the resulting cuboid.
Solution:
Volume of each cube = 125 cm3
∴ a3 = 125 cm3 ⇒ a = 5 cm
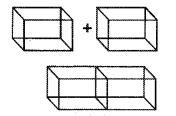
By joining these two cubes we get a cuboid, whose
length (l) = 10 cm
breadth (b) = 5 cm
height (h) = 5 cm
then the total surface area
= 2 (lb + bh + lh)
= 2(10(5) + 5(5) + 5(10))
= 2(50 + 25 + 50)
= 2(125) = 250 cm2
Question 14.
The base area of a cone is 616 sq.cm and its height is 48 cm. Find its total surface area.
Solution:
The base area of a cone = πr2 = 616 cm2
Given height of cone = 48 cm = h
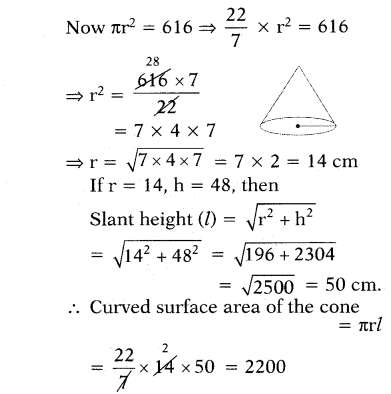
∴ Total surface area
= C.S.A + base area
= 2200 + 616 = 2816 cm2
Question 15.
Find the volume of largest right circular cone that can be cut out from a cube, whose edge is 7 cm.
Solution:
Volume of the cone (V) = 1/3 πr2h
[r = s/2 = h/2]
= 1/3 × 22/7 × 7/2 × 7/2 × 7
∴ V = 89.83 cm3
Question 16.
If half of the vertical angle of a cone of height 3 cm is 60°. Find its volume.
Solution:
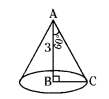
Let ‘B’ be the centre of base of the cone and BC is radius.
AB is vertical height (i.e.,)
AB = 3 cm
Given that ∠BAC = 60°
∆ABC is a right angled triangle, then
tan 60° = BC/AB
⇒ √3 = BC/3 ⇒ BC = 3√3 cm
Now we have h = 3 cm, r = 3√3 cm
Volume of the cone = 1/3 πr2h
1/3 π(3√3)2 × 3 = 27π cm3
(or)
= 594/7 = 84.86 cm3
Question 17.
Find the volume and total surface area of a hemisphere of diameter 7 cm. Take π = 22/7
Solution:
Diameter of hemisphere = 7 cm
∴ Radius of hemisphere = (r) = d/2 = 7/2 cm
Then volume of hemisphere = V = 2/3 πr3
= 2/3 × 22/7 × 7/2 × 7/2 × 7/2 = 22×49/12 = 89.83
Volume = 89.83 cm3
Total surface area of hemisphere = 3πr2
= 3 × 22/7 × 7/2 × 7/2 = 77×3/2 = 115.5 cm2
Question 18.
The length, breadth and height of a cuboid are (log 125 + log 8),
(log 1000 - log 10) and log 10 respectively. Find the total surface area of the cuboid.
Solution:
Length of cuboid (l) = (log 125 + log 8)
Breadth of cuboid (b)
= (log 1000 - log 10)
Height of cuboid (h) = log 10
∴ (l) = log (125 × 8)
= log 1000
= log 103 = 3 log 10 = 3
(b) = log 1000 - log 10
= log 1000/10
= log 100 = log 102 = 2
(h) = log 10 = 1
Then total surface area of cuboid
= 2(lb + bh + lh)
= 2(3 × 2 + 2 × 1 + 1 × 3)
= 2 (6 + 2 + 3) = 2(11)
= 22 square units.
Question 19.
The radius of a sphere is 3.5 cm. Find it’s surface area.
Solution:
Given, r = 3.5 cm
Surface area of sphere = 4πr2
= 4 × 22/7 × 3.5 × 3.5
= 88×12.25/7 = 154 cm2
Question 20.
Express the volume of a cone in terms of volume of right circular cylinder of the same base and height and explain how you arrived at it.
Solution:
We know that,
Volume of cone = 1/3 πr2h
Volume of cylinder = πr2h
Hence,
volume of cone : volume of cylinder
= 1/3 πr2h : πr2h
Hence, volume of cone = 1/3 × volume of cylinder.
Question 21.
The radius of a conical tent is 5m and its height is 12m. Calculate the length of the canvas used in making the tent if width of canvas is 2cm.
Solution:
Radius of the conical sent (r) = 5 m.
Height of the tent (h) = 12 m.
∴ Slant height of the cone
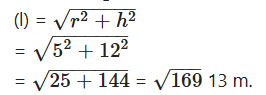
Now, surface area of the tent = πrl
= 22/7 × 5 × 13 = 1430/7 m2
Area of the canvas used = 1430/7 m2
It is given that the width of the canvas = 2m.
Length of the canvas used = Area/Width
= 1430/7 × 1/2
= 102.14 m
Question 22.
How many spherical balls can be made out of a solid cube of lead, whose edge measures 66 cm. and each ball being 3 cm in radius ?
Solution:
Side of the cube (s) = 66 cm
Radius of the spherical ball = r = 3 cm
Let the number of spherical balls that can be made = n
n × volume of a spherical ball = Volume of the cube
n × 4/3 πr3 = s3
n × 4/3 × 22/7 × 3 × 3 × 3 = (66)3
n = 66 × 66 × 66 × 3/4 × 7/22 × 1/3 × 1/3 × 1/3
= 2541
Number of spherical balls can be made = 2541
Question 23.
An oil drum is in the shape of cylinder, whose diameter is 2 m and height is 7 m. The painter charges ? ₹ 5 per m2 to paint the drum. Find the total charges to be paid to the painter for
10 drums.
Solution:
It is given that diameter of the (oil drum) cylinder = 2 m.
Radius of cylinder = d/2 = 2/2 = 1 m.
Total surface area of a cylindrical drum = 2πr(r + h)
= 2 × 22/7 × 1(1 + 7)
= 2 × 22/7 × 8 = 352/7 m2 = 50.28 m2.
So, the total surface area of a drum = 50.28 m2
Painting charge per 1 m2 = ₹ 5.
Cost of painting of 10 drums
= 50.28 × 5 × 10
= ₹ 2514
Question 24.
A hemisphere is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the Cube. Determine the total surface area of the remaining block.
Solution:
Let diameter of the hemisphere be ‘l’ = 21 cm
Radius of the hemisphere = l/2 = 21/2 cm
Also, length of the edge of the cube = l = 21 cm
∴ Total surface area of the remaining solid .
Question 25.
Two metallic spheres of radii 6 cm and 8 cm are melted along with another sphere and made into a big sphere of radius 12 cm. Find the radius of the third sphere.
Solution:
Radii of two metallic spheres
= r1 = 6 cm
r = 8 cm
Volume of the metallic spheres

⇒ 728 + x3 - 123
⇒ x3 = 123 - 728 = 1728 - 728
= 1000 cm
⇒ x = 10 cm.
Question 26.
Two cubes each of volume 216 cm3 are joined end to end together. Find the total surface area of the resulting cuboid.
Solution:
Given, volume of the cube V = a3 = 216 cm3
∴ a3 = 6 × 6 × 6 = 63
Hence a = 6 cm
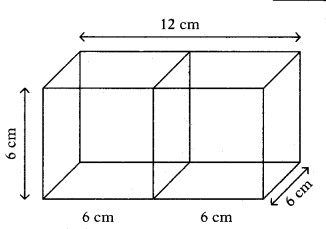
When two cubes are added, the length of cuboid = 2a = 2 × 6 = 12 cm,
breadth = a = 6 cm,
height = a = 6 cm is formed.
∴ T.S.A. of the cuboid = 2(lb + bh +lh)
= 2(12×6 + 6×6 + 12×6)
= 2(72 + 36 + 72)
= 2 × 180 = 360 cm2
∴ The surface area of resulting cuboid is 360 cm2.
Question 27.
What is area of required cloth to make 10 conical hats having 7 cm ground radius and 24 cm height ?
Solution:
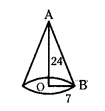
Ground radius of cone (r) = 7 cm
Height of cone (h) = 24 cm
Then its slant height
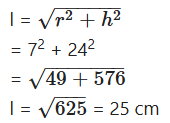
Then C.S.A. of the cone = Area of cloth required
= πrl = 22/7 × 7 × 25 = 550 cm2
Then the cloth required for 10 hats = 550 × 10 = 5500 cm2
Question 28.
A circle having 21 cm radius is cut into 3 equal parts to make 3 equal circular cones. Then what will be the radius of such cone ?
Solution:
Radius of the circle = 21 cm
Then the circumference of circle
= 2πr = 2 × 22/7 × 21 = 132 cm
1/3 of this circumference of circle = Circumference of the ground of the
cone
= 1/3 × 132 = 44 cm
Now let the ground radius of new cone = r
Then its ground circumference = 2πr = 44
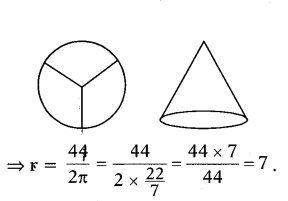
So ground radius of cone = 7 cm.
Question 29.
Define "Regular cone". Deduce formula for slant height of a regular cone.
Solution:
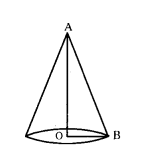
A solid having a circular base and vertex above the centre of circular base is called a regular cone.
A → Vertex
‘O’ centre of ground
OB is the radius of cone (r) and
0A is the height of cone (h)
AB is slant height (l)
Now ∆AOB is a right angled triangle.
Where ∠AOB = 90 and AB is hypotenuse.
Then from Pythagorus theorem
AB2 = OA2 + OB2 = r2 + h2
∴ AB = √r2+h2
∴ Slant hight (l) = √r2+h2
Question 30.
Draw a cone and label them.
Solution:

In the above cone
OB is the radius of the ground.
AO is the height of cone.
AB is slant height of cone.
Question 31.
Which kind of cones are formed by rotating on their axis of following triangles?
a) Equilateral
b) Right angled
c) Scalene
Solution:
a) Equilateral triangle : Having the altitude of this equilateral as rotat¬ing axis, on rotation we get a regular cone, (right cone)
b) Right angled triangle : Having a leg (a side other than hypotenuse) as rotating axis, on rotation of this right angled triangle we get a right circular cone.
c) Scalene triangle : Having a particular altitude from a vertex as rotating axis, on rotation we get a
cone
Question 32.
A sphere, a cylinder and a cone have the same radius and same height. Find the ratio of their volumes. (AS4) [Hint: Diameter of the sphere is equal to the heights of the cylinder and the cone.] A sphere, a cylinder and a cone have the same radius and same height.
Solution:
Sphere Cylinder Cone
Radius = r r r
Height = r 2r = h 2r = h
Now C.S.A of spehre = 4πr2 ......(1)
C.S.A of cylinder = 2πrh
= 2πr.2r-2r = 4πr2 ........ (2)
Now for cone, slant height = l
= √r2+h2
= √r2+4r2 ( ∵ h = 2r)
= √5r2 = √5(r)
Then C.S.A of cone = πrl = πr. √5r
= √5 πr2 ...... (3)
∴ Ratio of C.S.A of sphere, cylinder and cone = 4πr2 : 4πr2 : √5 πr2
= 4 : 4 : √5