AP 10th Class Maths Chapter 11 Important Questions Areas Related to Circles
1th Lesson Areas Related to Circles Class 10 Important Questions with Solutions
10th Class Maths Areas Related to Circles 1 Mark Important Questions
Question 1.
Find the circumference and area of a circle of radius 8.4 cm.
Solution:
Given radius of the circle = 8.4 cm
Circumference C = 2πr
= 2 × 22/7 × 8.4
= 52.8 cm
Area of the circle A = πr2
= 22/7 × 8.4 × 8.4
= 221.76 cm2
Question 2.
Find area of a circle whose circumference is 44 cm.
Solution:
Give circumference of the circle C = 44 cm
Let radius = 4
Circumference = 2πr = 44
= 2 × 22/7 r = 44
r = 44×7/2×22
r = 7 cm
Area of circle = πr2
= 22/7 × 7 × 7 = 154 cm2
Question 3.
Define minor sector.
Solution:
A sector of a circle is called a minor sector if the minor arc of the circle is a part of the boundary.
Shaded part of AOB is the minor sector.
Question 4.
Define major sector.
Solution:
A sector of a circle is called a major if the major arc of the circle is a part of its boundary.
Shaded part of POQ is the major sector.
Question 5.
Write the formula to find the length of arc.
Solution:
Length of arc l = x°/360° 2πr (or) x/180° πr.
Question 6.
Write the formula to find the area of a sector.
Solution:
Area of sector A = x°/360° πr2.
Question 7.
A pendulum swings through an angle of 30° and describe an arc 8.8 cm in length. Find the length of the pendulum.
Solution:
Given angle θ = 30°, l = 8.8 cm, r = ?
Length of an are
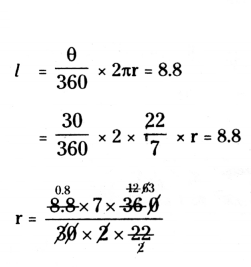
r = 0.8 × 7 × 3 = 16.8 cm
Question 8.
The radius of a circle is same as the side of a square. Find the ratio of their perimetrers.
Solution:
r = s
Perimeter of circle: Perimeter of square
2πr : 4r
πr : 2r
π : 2
Question 9.
Find the length of the arc of a circle of radius 14 cm which subtends an angle of 60° at the centre of the circle.
Solution:
θ = 60°, r = 14 cm
l = θ/360 × 2πr
= 60/360 × 2 × 22/7 × 14
1/6 × 2 × 22 × 2
= 22×2/3 = 44/3
Question 10.
If the radius of a semi-circular protractor is 7 cm, then find perimeter.
Solution:
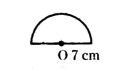
r = 7 cm
p = 36/7 r = 36/7 × 7 = 36 cm
Question 11.
Find the area of the sector of a circle of radius 6 cm whose centred angle is 30°. (Take π = 3.14)
Solution:
r = 6 cm
θ = 30°
Area of sector = θ/360 × πr2
= 30/360 22/7 × 6 × 6
= 1/12 × 22/7 × 36
= 11×36/6×7
= 11×6/7
= 66/7 cm2
Question 12.
Find the area of a quadrant of a circle where the circumference of circle is 176 m.
Solution:
θ = 90°
Circumference = 176 m
2πr = 176
2 × 227 × r = 176
r = 176 × 7/22 × 12
r = 8×7/2
r = 28 cm
A = θ/360 × πr2
= 90/360 × 22/7 × 28 × 28
= 1/4 × 22 × 4 × 28
= 11 × 2 × 28
A = 616 cm2
Question 13.
The minute hand of clock is 84 cm long. Find the distance covered by the tip of minute hand from 10 : 10 am to 10 : 25 am.
Solution:
60 min → 360
1 min → 6°
10 : 10 to 10 : 25 AM mean 15 min
15 min = 15 × 6° = 90°
θ = 90°
l = θ/360 × 2πr
= 90/360 × 2 × 22/7 × 84
1/4 × 2 × 22/7 × 84
= 11 × 12
l = 132 cm
Question 14.
The diameter of a car wheel is 42 cm. Find the number of complete revolutions it will make in moving 132 km.
Solution:
d = 42 cm
r = 21 cm
Circumference = 2πr
= 2 × 22/7 × 21
= 44 × 3
= 132 cm
No. of revolutions
= 132×104/132 = 104 (∵ 132 km = 1320000 = 132 × 104)
Question 15.
Find the area of a square that can be inscribed in a circle of area 14087 cm2.
Solution:
πr2 = 1408/7
22/7 × r2 = 1408/7
r2 = 1408/22
r2 = 704/11
r2 = 64
r = 8 cm
Question 16.
A circular arc of length 22 cm subtends an angle θ at the centre of the circle 21 cm. Find the value of θ.
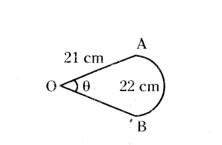
Solution:
l = 22 cm
r = 21 cm
l = θ/360 × 2πr
22 × θ/360 × 2 × 22/7 × 21
1 = θ/180 × 3
θ/60 = 1
θ = 60°
Question 17.
Find the perimeter of the sector of a circle of a radius 14 cm and central angle 45°.
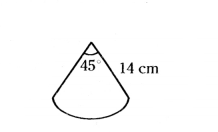
Solution:
r = 14 cm
θ = 45°
Perimeter = l + 2r
= θ/360 × 2πr + 2r
= 45/360 × 2 × 22/7 × 14 + 2 × 14
= 1/8 × 2 × 22 × 2 + 28
= 11 + 28
= 39 cm
Question 18.
Two concentric circles are at O. Find the area of shaded region, if outer and inner radii are 14 cm and 7 cm respectively.
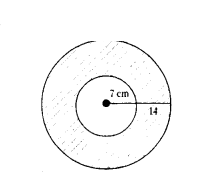
Solution:
R = 14 m
r = 7 m
Area of shaded region = π(R2 - r2)
= 22/7(142 - 72)
= 22/7(196 - 49)
= 22/7 × 147
= 22 × 21
= 462 cm2
Question 19.
The circumference of two circles are in the ratio 4 : 5. What is the ratio of their radii?
Solution:
2πr1 : 2πr2= 4 : 5
r1 : r2 = 4 : 5
Question 20.
If the perimeter of a circle is equal to that of a square, then find the ratio of their areas.
Solution:
4s = 2πr
⇒ s = πr/2 ⇒ s2 = πr2
⇒ (πr/2)2 : πr2 ⇒ π2r2/4 : πr2
⇒ π/4 : 1 [π = 22/7] ⇒ 14 : 11
Question 21.
If the radii of two circles are in the ratio of 4:3, then find the ratio of their areas.
Solution:
r2 : r2 = 4 : 3
⇒ πr12 : πr22
⇒ π 42 : π 32
⇒ 16 : 9
Question 22.
Find the area of a quadrant of a circle of radius 7 cm.
Solution:
r = 7
Area of quadrant = πr2/4
= 22×7×7/7×4
= 11×7/2
= 77/2 cm
Question 23.
Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°. (Take π = 227)
Solution:
r = 6 cm
θ = 60°
Area of sector = θ/360 × πr2
= 60/360 × 22/7 × 6 × 6 cm2
= 132/7 cm2
Question 24.
A horse tied to a pole with 28m long rope. Find the perimeter where the horse can graze. (Take π = 22/7)
Solution:
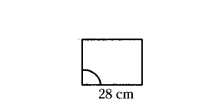
r = 28 cm
θ = 90°
Perimeter = 2πr
= 2 × 22/7 × 28 = 44 × 4 = 176 cm
Question 25.
In a circle of diameter 42 cm, if an arc subtends an angle of 60° at the centre where π = 22/7 then find the length of the arc.
Solution:
θ = 60°
d = 42 cm
r = 21 cm
l = θ/360 × 2πr
= 60/360 × 2 × 22/7 × 21
= 16 × 2 × 22 × 3 = 22 cm.
Question 26.
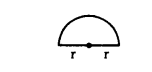
Find the perimeter of a semicircular protractor whose radius is r.
Solution:
P = πr + 2r
Question 27.
If the circumference of a circle increases from 2π it to 4π then its area ....... the original area.
Solution:
C = 2πr
If r = 1
C = 2π
A = π(r)2 = π(1)2 = π
2πr = 4π
r = 2
New area = πr2 = π(2)2
= 4π = 4 × old area
Question 28.
If the difference between the circumference and the radius of a circle is 37cm, π = 22/7, find the circumference (in cm) of the circle.
Solution:
2πr - r = 37 cm
(2 × 22/7 - 1) r = 37
(44-7/7)r = 37
37/7 r = 37
r = 7
C = 2πr
= 2 × 22/7 × 7
= 44 cm
Question 29.
Area of a sector of a circle is 1/6 to the area of circle. Find the degree measure of its minor arc.
Solution:
θ/360 × πr2 = 1/6 × πr2
θ/360 = 1/6
θ= 60°
Question 30.
Figure is a sector of circle of radius 10.5 cm, find the perimeter of the sector. (Take π = 22/7)
Solution:
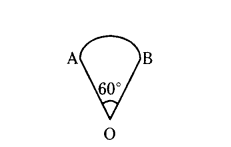
r = 10.5 cm
θ = 60°
P = l + 2r
= θ/360 × 2πr + 2r
= 60/360 × 2 × 22/7 × 10.5 + 2(10.5)
= 1/6 × 2 × 22 × 1.5 + 21
= 22 × 0.5 + 21
= 11 + 21
= 32 cm
Question 31.
Assertion (A) : Area of sector if l = 10 cm, r = 9 cm is 10.5 cm
Reason (F) : Area of sector = θ/360 × πr2
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) A is true, R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
D) A is false, R is true.
Question 32.
Assertion (A) : Area of circle with 1 cm radius is ? cm2.
Reason (R) : Length of the arc of the sector (l = θ/180 × 2πr
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) A is true, R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
C) A is true, R is false.
Question 33.
Assertion (A): Rddius of a circle is = 7/√π cm then area is 49 sq. units.
Reason (R) : Area of circle = πr2.
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) A is true, R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
Question 34.
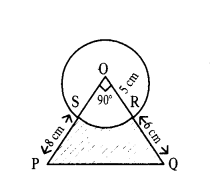
Assertion (A): If a chord of length equal to the radius in a triangle then the triangle formed with that chord is an equilateral triangle.
Reason (R) : Area of ring π(R2 - r2).
A) Assertion (A) is true, Reason (R) is true and R is the correct explanation of A.
B) A is true, R is true, but R is not the correct explanation of A.
C) A is true, R is false.
D) A is false, R is true.
Solution:
B) A is true, R is true, but R is not the correct explanation of A.
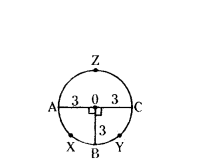
Question 35.
Observe the figure, match the column.
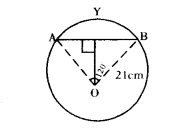
A) Area of segment AYB
B) Area of sector OAYB
i) 441/4√3
ii) 21/4(88 - 21√3)
iii) 462
iv) 21/2
Solution:
A - i, B - iii
Question 36.
Choose correct matching.
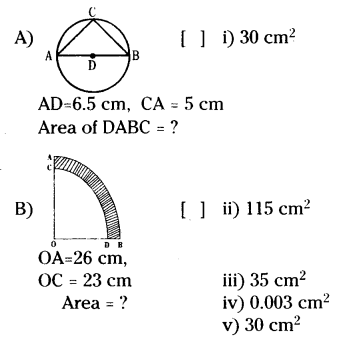
Answer:
A - (i), B - (ii).
Question 37.
Draw a rough diagram of minor segment of a circle and shade it.
Answer:
Question 38.
What do we call the part a and b in the below circle ?
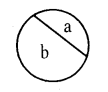
Solution:
‘a’ is minor segment and ‘b’ is major segment.
10th Class Maths Areas Related to Circles 2 Marks Important Questions
Question 1.
Find the area of quadrant of a circle whose circumference is 22 cm.
Solution:
Let radius = 4 cm
Circumference C = 2πr = 22 cm
= 2 × 22/7 × r = 22
r = 22×7/2×22 = 7/2 cm
Area of a quadrant = 14 πr2
= 1/4 × 22/7 × 7/2 × 7/2
Therefore, area of quadrant = 77/8 = 9.625 cm2
Question 2.
The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.
Solution:
Let the radius = r cm
Circumference = diameter + 16.8
2 × 22/7 r = 2r + 16.8
44r = 7 (2r + 16.8) = 14r + 16.8 × 7
44r - 14r = 117.6
30r = 117.6
r = 117.6/30 = 3.92 cm
Therefore, radius r = 3.92 cm.
Question 3.
A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Solution:
Let the radius of the circle r cm
Distance covered by wheel in 1 revolution = Total distance moved/Number of revolutions
= 11/5000km = 11×1000×100/5000
That is circumference of wheel = 220 cm
So, 2πr = 220
2 × 22/7 r = 220
r = 220 × 7/2×22 = 35 cm
Diameter d = 2 × r = 2 × 35 = 70 cm
Question 4.
A wheel has diameter 84 cm. Find how many complete revolutions must it take to cover 792 m.
Solution:
Let radius of wheel
r = Diameter/2 = 84/2 = 42 cm
Circumference of the wheel
2πr = 2 × 22/7 × 42 = 264 cm = 2.64 m
No. of revolutions made to 792 m = 792/2.64 = 300
Question 5.
Find the perimeter of a quadrant of a circle of radius 14 cm.
Solution:
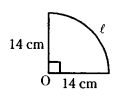
θ = 90°
r = 14 m
Perimeter of quadrant of cricle
= l + 2r =θ/360 × 21r + 2r
= 90/360 × 2 × 22/7 × 14 + 2 × 14
= 1/4 × 2 × 22 × 2 + 28
= 22 + 28 = 50 cm
Question 6.
Find the diameter of a circle whose area is equal to the sum of the areas of the two circles of radii 24 cm and 7 cm.
Solution:
Given r1 = 24 cm, r2 = 7 cm
πR2 = πr12 + πr22
R2 = 242 + 72
R2 = 576 + 49
R2 = 625
R = 25 cm
Diameter, d = 2R = 50 cm
Question 7.
Find the area of circle whose circumference is 22.
Solution:
Circumference of circle = 22 m
2πr = 22
2 × 22/7 × r = 22
2r/7 = 1
r = 72 m
Area of circle =πr2
= 22/7 × 7/2 × 7/2 cm2
= 77/2 cm2
Question 8.
Find the diameter of a circle whose area is equal to the sum of the areas of two circles of radii 40 cm and 9 cm.
Solution:
Given r1 = 40 cm, r2 = 9 cm
πR2 = πr12 + πr22
R2 = r12 + r22
R2 = 402+ 92
R2 = 1600 + 81
R2 = 1681
R = √1681
R = 41 cm
Diameter = 2 × 41 cm = 82 cm
Question 9.
A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of minor segment. (Use π = 3.14)
Solution:
Radius, r = 10 cm
θ= 90°
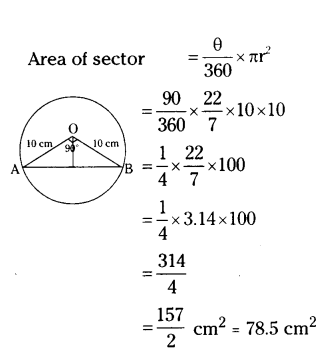
Area of right-angled triangle
= 1/2 × 10 × 10 = 50 cm2
Area of minor segment = Area of sector - Area of right triangle
= 78.5 - 50 = 28.5 cm2
Question 10.
A piece of wire 22 cm long is bent into the form an arc of a circle subtending an angle of 60° at its centre. Find the radius of the circle.
Solution:
Given l = 22 cm
θ = 60°
l = ?/360 × 2πr
22 = 60/360 × 2 × 227 × r
1 = 1/6 × 2 × 1/7 × r
1 = r/21
r = 21 m
radius = 21 cm
Question 11.
An iron wire when bent in the form of a square encloses an arrea of 121 cm2. If the same wire is bent in the form of a circle, then find the circumference of circle.
Solution:
Area of square = 121 m2
S2 = 121
⇒ S = √121
S = 11 cm
⇒ 4S = 4 × 11 = 44 cm
2πr = 44
⇒ 2 × 22/7 × r = 44
r = 7 cm
Area of circle = πr2
= 22/7 × 7 × 7 cm2
= 154 cm2
Question 12.
If the radius of the circle is 6 cm and the length of an arc is 12 cm. Find the area of sector.
Solution:
Radius, r = 6 cm
Length of arc, l = 12 cm
Area of sector = ?r/2
= 12×6/2
= 6 × 6
= 36 cm2
Question 13.
PA is the tangent drawn to a circle of whose centre is ‘O’, OA is the radius and P is the external point of the circle. If PA = 24 cm, OP = 25 cm., then find its radius.
Solution:
Given PA = 24 cm, OP = 25 cm
We have OP2 = OA2 + PA2
⇒ (25)2 = OA2 + (24)2
⇒ 625 = OA2 + 576
⇒ OA2 = 49
⇒ OA = 7 cm
Question 14.
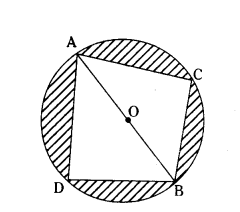
OABC is a Rhombus whose three vertices A, B and C lie on a circle with centre ‘O’. If the radius of the circle is 10 cm. Find the area of the Rhombus.
Solution:
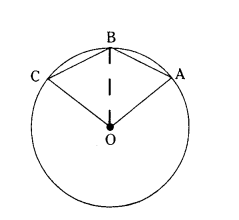
Join OB
Now OA = OB (radii)
OA = OB (Sides of Rhombus)
∴ ∆OAB is an equilateral triangle.
Area of equilateral ∆OAB
= √3/4 a2 = √3/4 × (10)2 = 25√3 cm2
∴ Area of Rhombus = 2 × area of ∆OAB
= 2 × 25√3 cm2
= 50√3 cm2
Question 15.
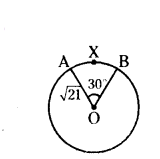
The minute hand of a clock is √21 cm long. Find the area of described by the minute hand on the face of the clock between 7 : 00 am to 7 : 05 am (π = √22/7)
Solution:
60 min → 360°
1 min → 360°/60° = 6°
Time between 7 am to 1 : 05 am = 5 min
Angle = 5 × 6°= 30°
Radius, r = √21 cm
Area swept = θ/360 × πr2
= 30°/360° × 227 × √21 × √21 = 1/12 2/27 × 21
= 11/2 m2 = 5.5 m2
Question 16.
Find the area of quadrant of a circle, where the circumference of a circle is 44 cm. (π =√22/7)
Solution:
2πr = 44
2 × 22/7 × r = 44
r = 7 cm,
θ = 90°
Area of quadrant = θ/360 × πr2
= 90°/360° × 22/7 × 7 × 7 cm2
= 1/4 × 22 × 7cm2 = 77/2 = 38.5 cm2
Question 17.
Find the area of a sector of a circle whose radius is 7 cm and angle at the centre is 60°.
Solution:
Radius = 7 cm, Angle at centre = 60°
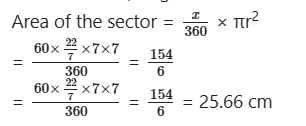
Question 18.
Find the area of a sector whose radius is 10 cm. and which make right angle at the center. (Take π = 3.14).
Solution:
Radius of the sector = 10 cm
Angle of sector = x° = 90°

Question 19.
Find the area of a sector whose radius is 10 cm. and which make right angle at the center. (Take π = 3.14).
Solution:
Radius of the sector =10 cm
Angle of sector = x° = 90°
Area of sector = A = x°/360° × πr2
= 90/360 × 3.14 × (10)2
= 1/4 × 3.14 × 100
= 1/4 × 314 = 78.5 cm2
Question 20.
Find the area of the shaded part in the given figure.

Solution:
Area of shaded part = Area of semi-circle - Area of triangle
= πr2/2 - 1/2 bh
= 22/7×7×7/2 - 1/2 × 14 × 6
= 11 × 7 - 7 × 6
= 77 - 42 = 35 sq. cm.
10th Class Maths Areas Related to Circles 4 Marks Important Questions
Question 1.
A horse is tied to a pole with 28 m long string. Find the area where the horse can graze.
Solution:
Given horse can graze the circular and radius r = 28 m
Area of land grazed by horse
= πr2 = 22/7 × 28 × 28 = 2464 m2
Question 2.
The circumferences of two circle s are in the ratio 2 : 3. Find their areas.
Solution:
Let radius of circules are r1 : r2
Ratio of their circumferences
= 2πr1 : 2πr2 = 2 : 3
= r1 : r2 = 2 : 3
Areas = πr12 : 2πr22
= 22/7 × 22 and 22/7 × 32
= 88/7 m2 and 198/7 m2
Question 3.
If a square is inscribed in a circle. Find the ratio of the areas the circle and the square.
Solution:
Let side of square = x units
area of square = x.x = x2 sq. units.
diagonal of square = √2.Side = √2.x
radius r = Length of diagonal/2
= √2.x/2 units
Area of circle = πr2
= π.(√2.x/2)2
= π.2.x/4
= πx2/2
Area of circle : Area of square
= πx2/2 : x2 = π/2 = : 1
Therefore, ratio = π : 2
Question 4.
A sector is cut from a circle of radius 21 cm, the angle of the sector is 150°. Find the length of its arc and area.
Solution:
Given radius r = 21 cm and θ = 150°,
Length of arc
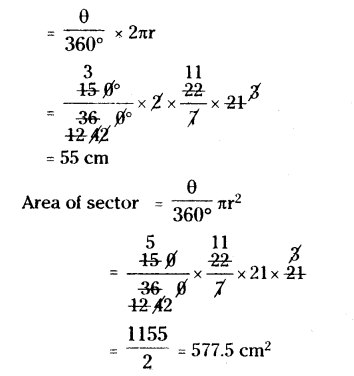
Question 5.
Find the angle subtended at the centre of a circle of radius 5 cm by an arc of length 5θ/3 cm.
Solution:
Radius of circle r = 5 cm
Let angle = θ
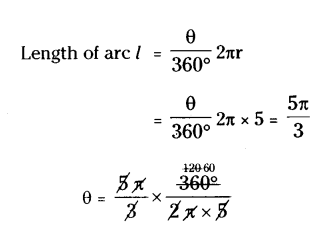
Therefore, angle subtended at the centre θ = 60°
Question 6.
A drain cover is made from a square metal plate of side 40 cm having 441 holes of diameter 1 m each drilled in it. Find the area of the remaining square plate.
Solution:
Side of square S = 40 cm, radius = d/2 = 1/2 cm
Area of square = S.S = 40 × 40 = 1600 cm2
Area of each hole
= πr2 = 22/7 (1/2)2 = 11/14 cm2
Area of 441 holes
= 441 × 11/14 = 346.5 cm2
Area of the remaining plate = 1600 - 346.5 = 1253.5 cm2
Question 7.
The area of a circular play ground is 22176 cm2. Find the cost of fencing this ground at the rate of ₹ 50 per metre.
Solution:
πr2 = 22176
22/7 × r2 = 22176
r2 = 22176 × 7/22
r2 = 1008 × 7
r2 = 7056
r = 84 m
2πr = 2 × 22/7 × 84
= 44 × 12
= 528 cm
c = 528/100 cm
c = 5.28 m
Cost of fencing per metre = ₹ 50
Total cost = 50 × 5.28 = ₹ 264
Question 8.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find the area of the sector formed by the arc. Also, find the length of the arc.
Solution:
r = 21 cm
θ = 60°
Area of sector = θ/360 × πr2
= 60/360 × 22/7 × 2/1 × 2/1 = 1/6 × 22 × 3 × 21
= 11 × 21 = 231 = cm2
Lenth of arc of sector = θ/360 × 2πr
= 60°/360° × 2 × 22/7 × 2/1 = 1/6 × 2 × 22 × 3 = 22 cm
Question 9.
Find the area of the sector of a circle of radius 6 cm and of central angle 90°. Also, find the area of corresponding major sector.
Solution:
r = 7 cm
θ = 90°
area of sector = θ/360 × πr2
= 90°/360° × 22/7 × 7 × 7 cm2
= 1/4 × 22 × 7 cm2
= 77/2 cm2 = 38.5 cm2
Area of major sector = Area of circle - area of minor sector
= πr2 - 38.5 cm2
= 22/7 × 7 × 7 cm2 - 38.5cm2
= 154 - 38.5 cm2
= 119.5 cm2
Question 10.
Find the area of the minor segment of a circle of radius 42 cm, if length of the corresponding arc is 44 cm.
Solution:
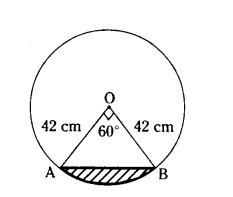
r = 42 cm
l = 44 cm
44 = θ/360 × 2πr
44 = θ/360 × 2 × 22/7 × 42
1 = θ/360 × 6
θ = 60°
∆OAB is an equilateral triangle.
Area of ∆OAB = √3/4 a2
= √3/4 × 42 × 42
= √3/2 × 21 × 42
= 21 × 21 √3
= 441√3 m2
Area of sector = θ/360 × πr2
= 60°/360° × 22/7 × 42 × 42
= 1/6 × 22 × 6 × 42
= 22 × 42
= 924 cm2
Area of minor segment = Area of sector - area of triangle
= (924 - 441√3 ) cm2
Question 11.
In the given figure, two concentric circles with centre O are shown. Radii of the circles are 2 cm and 5 cm respectively. Find the area of the shaded region.
Solution:
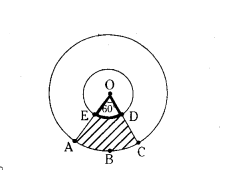
Given θ = 60°
r1 = 2 cm
r1 = 5 cm
Area of big sector = θ/360 × πr22
= 60°/360° × 22/7 × 5 × 5
= 1/6 × 22/7 × 25
= 11×25/21 = 275/21 cm2
Area of small sector = 60°/360° × πr22
= 1/6 × 22/7 × 22
= 1/6 × 22/7 × 4 = 44/21
Area of shaded region = 275/21 - 44/21
= 231/21 cm2
Question 12.
In the given figure, ‘O’ is the centre of circle such that diameter AB =13 cm and AC =12 cm. BC is joined. Find the area of shaded region (use = 3.14)
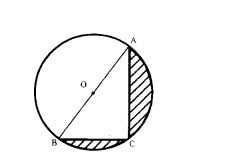
Solution:
‘O’ is the centre of circle
AB is the diameter.
AB = 13 cm
AC = 12 cm
∠ACB = 90° (Angle is a semi circle)
∴ ∆ACB is a right angled triangle.
AB2 = AC2 + BC2
132 = 122 + BC2
169 - 144 = BC2
BC2 = 25
BC = √25
BC = 5 cm
Ar ∆ACB = 1/2 × BC × AC
= 1/2 × 5 × 12 cm2
= 30 cm2
r = 13/2 cm
Area of semi circle
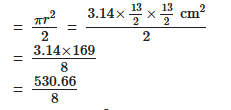
= 66.33 cm2
Area of shaded region = 66.33 - 30 cm2 = 36.33 cm2
Question 13.
In the figure, sectors of two concentric circles of radii 7 cm and 3.5 cm are given. Find the area of shaded region. (π = 22/7)
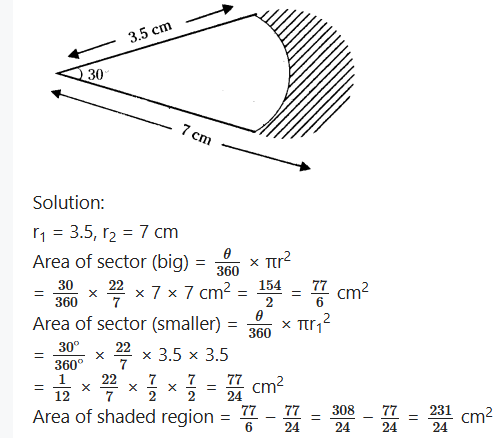
Question 14.
Find the area of the corresponding major sector of a circle of radius 28 cm and the central angle is 45°.
Solution:
r = 28 cm, θ = 45°
Area of minor sector = θ/360° × πr2
= 45°/360° × 22/7 × 28 × 28 cm2
= 1/8 × 22 × 4 × 28 cm2 = 28 × 11 cm2 = 616 cm2
Area of major sector= Area of circle - Area of minor sector
= πr2 - 616 cm2
= 22/7 × 28 × 28 - 28 × 11 cm2
= 28[22/7 × 28 - 11] = 28[88 - 11]
= 28 × 77 = 2156 cm2
Question 15.
In the figure AOB is a sector of angle 60° of a circle with centre ‘O’ and radius 17 cm. If AP⊥OB and AP = 15 cm then find the area of shaded region.
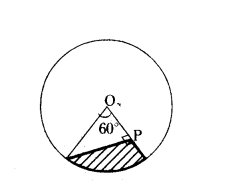
Solution:
θ = 60°
r = 17 cm
Area of sector = θ/360° × πr2
= 60°/360° × 22/7 × 17 × 17 = 1/6 × 22/7 × 289 cm2
11×289/21 = 3179/21 cm2
Area of ∆OPA:
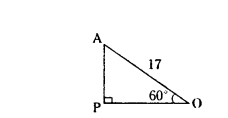
AP⊥DB
∠APO = 90°
∠AOP = 60°
∠PAO = 180° - 90° - 60°
= 180 - 150° = 30°
cos 60° = PO/17
1/2 = PO/17
PO = 17/2 = 8.5
sin 60° = AP/17
√3/2 = AP/17
AP = 8.5√3 cm
Area of ∆OAP = 1/2 × OP × AP
= 1/2 × 8.5 × 8.573 = 72.25√3/2
Area of shaded region = Area of sector - Ar ∆OAP
= 31792 - 72.25√3/2 cm2
Question 16.
A wire when bent in the form of an equilateral triangle encloses an area of 121√3 cm2. If the wire is bent in the form of a circle find the area enclosed by the circle. (Use π = 22/7)
Solution:
Area of equilateral triangle = 121√3 cm2
√3/4 a2 =121√3
a2 = 121 × 4
a = 11 × 2
a = 22 cm
Perimeter = 3a = 66 cm
2πr = 66 cm
2 × 22/7 × r = 66 ⇒ 2 × 17 × r = 3
r = 21/2 cm
Area of circle = πr2
= 22/7 × 21/2 × 21/2 cmsup>2 11 × 3 × 21/2 cm2
= 33×21/2 cm2 = 33 × 10.5 cm2 = 346.5 cm2
Question 17.
Find the area of shaded region in the figure, if BC = BD = 8 cm, AC = AD = 15 cm and ‘O’ is the centre of the circle (Take π = 3.14)
Solution:
‘O’ is centre of circle
AC = AD = 15 cm
BC = BD = 8 cm
∆ACB and ∆ADB are right angled triangles
∴ ∠ACB = 90° = ∠ADB
AB2 = AC2 + BC2
AB2 = 152 + 82
AB2 = 225 + 64
AB2 = 289
AB = √289
AB = 17 cm
r = 17/2 cm
ar ∆ABC = 1/2 × BC × AD = 1/2 × 8 × 15 = 60 cm2
ar ∆ADB = 60 cm2
∴ Area of two triangles = (60 + 60) cm2 = 120 cm2
Area of shaded region = Area of circle - Area of both triangles
= πr2 - 120 cm2
= 3.14 × 17/2 × 17/2 - 120 cm2
= 3.14 × 8.5 × 8.5 - 120 cm2
= 226.865 - 120 cm2
= 106.865 cm2
Question 18.
In the given figure, a semi circle of radius 7 cm is inscribed in a rectangle. Find the area of shaded region.

Solution:
In a semi circle r = 7 cm
Area = πr22 = 22/7 × 7 × 7/2
= 11 × 7 = 77 cm2
In a rectangle,
l = 7 + 7 = 14 cm
b = 7 cm
Area = 7 × 14 = 98 cm2
Area of shaded region = 98 - 77 cm2 = 21 cm2
Question 19.
Find the area of the shaded region in the given figure.
ABCD is a square of side 10.5 cm.
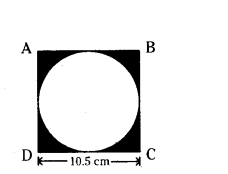
Solution:
Side of the Square = 10.5 cm
Radius of the circle (r) = 10.5/2
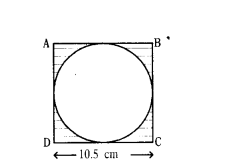
Area of the square = (Side)2 = (10.5)2 = 110.25 cm2
Area of the circle = pr2
= 22/7 × 10.5/2 × 10.5/2 = 86.625 cm2
Area of the shaded region = Area of the square - Area of the circle
= 110.25 - 86.625
= 23.625cm2
Question 20.
A chord of a circle of radius 10 cm. subtends a right angle at the centre. Find the area of the corresponding minor segment (use p = 3.14).
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
Area of sector OACB = x/360 × πr2
= 90°/360° × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of D AOB = 1/2 × 10 × 10
= 50 cm2
Area of the Minor Segment = Area of sector OACB - Area of D OAB
= 78.5 - 50.0 = 28.5 cm2
10th Class Maths Areas Related to Circles 8 Marks Important Questions
Question 1.
Find the area of the shaded region of the given figure, where a circular arc of radius 6 cm has been drawn with vertex of an equilateral triangle OAB of side 12 cm as centre.
Solution:
Given radius of the circle r = 6 cm
Side of triangle = 12 cm
Angle in the minor sector (or) angle in the equailateral triangle = 60°
Angle in the major sector θ = 360° - 60° = 300°
Area of the shaded region = (Area of equailateral triangle + Area of major sector)
= (√3/4 a2 + θ/360 πr2)
= √3/4 × 12 × 12 + 300/360 × 3.14 × 6 × 6
= (36√3 + 30 × 3.14)
= 114.235 + 92.2
= 208.435 cm2
Therefore, area of the shaded region
= 208.435 cm2
Question 2.
In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find
i) Length of the arc
ii) Area of the sector formed by the arc.
iii) Area of the segment formed by the corresponding chord of the arc.
iv) Find the area of the major segment.
Solution:
Given radius of the circle = 21 cm
Angle subtended by the arc θ = 60°

= 231 - 19.953
Area of minor segment = 40.047 cm2
iv) Area of major segment
= Area of circle - Area of minor segment
= πr2 - 40.047
= 22/7 × 21 × 21 - 40.047
= 1386 - 40.047
Therefore, area of major segment
= 1345.953 cm2
Question 3.
The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Solution:
Given length of clock (or) radius of circle r = 14 cm
Angle made by the minute hand in 5 minutes = θ = 30°
Area of the sector
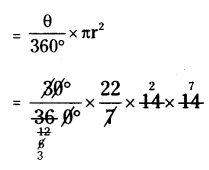
Area swept by the minutes hand in 5 minutes = 154/3 cm2
Question 4.
Find the area of the sector of a circle with radius 4 cm and of an angle 30°. Also find the area of the corresponding major sector.
Solution:
Given radius of the circle r = 4 cm
Angle of the sector θ = 30°
Area of the sector (OAXB)
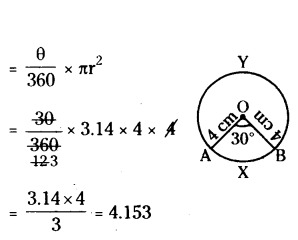
Therefore area of the sector = 4.153 cm2
Area of the corresponding major sector
= Area of sector OAYB
= Area of the circle - Area of OAXB
= πr2 - x/360 πr2 = (1 - x/360)πr2
= (1 - 30/360 ) × 22/7 × 4 × 4
= (1/1 - 1/12) × 3.14 × 4 × 4
= (12?1/12) × 3.14 × 4 × 4
= 11/12 × 3.14 × 4 × 4 = 46.05 cm2
Therefore, area of the corresponding major sector = 46.05 cm2
Question 5.
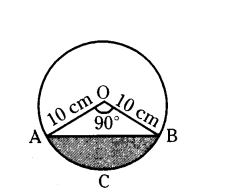
In a circle with centre O and radius 5 cm, AB is a chord of length 5√3 cm.
Find the area of the sector AOB.
Solution:
Given the radius of circle
OA = OB = r = 5 cm
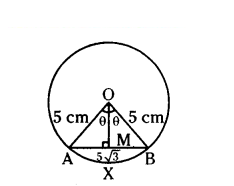
Length of the chord AB = 5√3 cm
Draw OM⊥AB, OM bisects AB
That is AM = BM = 5√3/2
In ∆AOM, ∠OMA = 90°, ∠AOM = θ
sin θ AM/OA = 5√3/2/5 = √3/2 sin 60°
Therefore θ = 60°
That is ∠AOB = 2 × 60 = 120
Area of sector OAXB
= ∠AOB/360 × πr2 = 120/360 × 3.14 × 5 × 5
Area of sector OAXB = 3.14/3 × 5 × 5
= 78.5/3 = 26.17 cm2
Question 6.
An arc of length 20π cm subtends an angle of 144° at the centre of a circle. Find the radius of the circle.
Solution:
Given length of the arc = 20π cm,
Let radius = r cm
Angle subtended by arc θ = 144°
Length of the arc l = θ/360 × 2πr
= 144/360 × 2πr = 20π
r = 20π×360/144×2π
Therefore, radius of circle r = 25 cm
Question 7.
The minute hand of a clock is √21 cm long. Find the area described by the minute hand on the face of the clock between 7.00 AM and 7.05 AM.
Solution:
Given the length of minute hand = radius of circle r = √21 cm
= θ/360 × πr2
= 30/360 × 22/7 × √21 × √21
= 30/360 × 22/7 × 21
= 11/2 = 5.5 cm2
Area described by the minute hand in 5 minutes = 5.5 cm2
Question 8.
The minute hand of a clock is 10 cm long. Find the area of the face of the clock described by the minute hand between 8 AM and 8.25 AM.
Solution:
Given length of the minute hand = Radius of the circle (r) = 10 cm
Minute hand makes the angle by moving 25 minutes at the centre θ = 150°
Area described by the minute hand
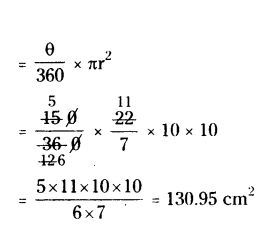
Area described by the minutes hand in 25 minutes = 130.95 cm2
Question 9.
A horse is placed for grazing inside a rectangular field 70 m by 52 m and is togethered to one corner by a rope 21 m long. On how much area can it graze ?
Solution:
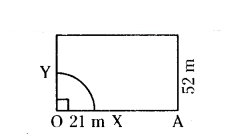
Given
Radius of the sector r = 21 m
Angle of the sector θ = 90°
Area of the sector = θ/360 × πr2
= 90/360 × 22/7 × 21 × 21
= 11×21×3/2
= 346.5 cm2
Therefore, area to be grazed by the horse = 346.5 cm2
Question 10.
ABCD is a flower bed. If OA = 21 m and OC = 14 m, find the area of the bed.
Solution:
Given the radius of large sector (or) OA = OB = 21 m A
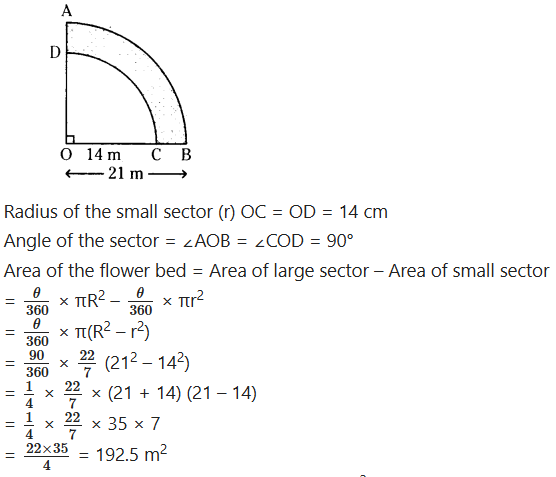
Therefore, area of the flower bed = 192.5 m2
Question 11.
ABCD is a quadrant of a circle of radius 14 cm with AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
Solution:
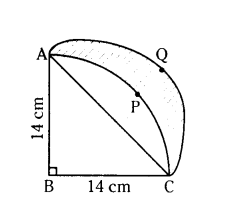
Given in ∆ABC, ∠B = 90°
AB = BC = 14 m
AC2 = AB2 + BC2
AC = √142+142
= √142×22
AC = 14√2cm
Diameter of semi circle AC = 14√2 Radius of semi circle
= AC/2 = 14√2/2= 7√2 cm
Area of shaded portion
= Area of APCQA
= Area of ACQA - Area of ACPA
= Area of semi circle - (Area of ABCPA - Area of ∆ABC)

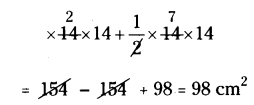
Area of shaded portion = 98 cm2
Question 12.
On a circular table cover of radius 32 cm a design is formed leaving an equilateral triangle ABC in the middle as shown in figure. Find the area of the design.
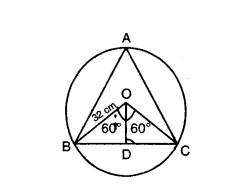
Solution:
Given ∆ABC is an equilateral triangle.
That is ∠A = ∠B = ∠C = 60°
and AB = BC = AC
Radius of the circle OA = OB = OC = 32 cm
Each side of ∆ABC can make the angle at the centre is 120°
So, θ = ∠BOC = 120°
Draw OD⊥BC
That is OD bisects BC and ∠BOC
BD = CD = BC/2
∠BOD = ∠COD = 1/2 ∠BOC
= 1/2 × 120 = 60°
In ∆OBD, ∠ODB = 90°

BC = 2.BD = 2 × 16√3 = 32√3 cm
Area of shaded region = 3 (area of sector - area of ∆ABC)

= 1888.11 cm2
Area of the shaded region = 1888.11 cm2
Question 13.
In the given figure O is the centre of the circle of radius 28 cm. Find the area of minor segment AXB.
Solution:
Given radius of the circle (r)
OA = OB = 28 cm
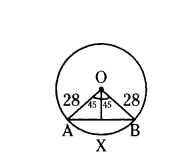
Angle at sector ∠AOB (θ) = 90°
Area of minor segment = Area of sector - Area of ∆AOB
= θ/360 πr2 - 1/2 × AB × OX
In ∆AOB, ∠AOB = 90°,
Draw OX⊥AB
OX bisects AB and ∠AOB
that is AX = BX = AB/2
and ∠AOX = ∠BOX = ∠AOB/2
∠AOX = ∠BOX = 90/2 = 45°
In ∆AOX, ∠AOX = 45°

= 22 × 28 - 14 × 14 × √2 × √2
= 616 - 392 = 224 cm2
Therefore, area of minor segment = 224 cm2
Question 14.
From a circular piece of cardboard of radius 3 cm two sectors of 90° have been cutoff. Find the perimeter of the remaining portion nearest hundredth
centimeters (π = 22/7).
Solution:
Given radius of the circle r = 3 cm
Angle of each sector θ = 90°
that is quadrant circle
two quadrant circles = semi circle
So, remaining portion is a semi circle
Perimeter of semi circle = πr
= 22/7 × 3 22/7 = 9.428 cm
Question 15.
A square OABC is inscribed in a quad-rant OPBQ of a circle. If OA = 21 cm find the area of the shaded region.
Solution:
Given OA = AB = BC = OC = 21 cm
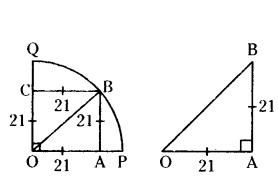
OB2 = OA2 + AB2
OB2 = 212 + 212 = 2 × 212
OB = √2×212= 21√2 cm
So, radius of the circle
OP = OB = OQ = 21√2 cm
Area of the shaded region = Area of OPBQ - Area of OABC
= 1/4πr2 - OA × AB
= 1/4 × 22/7 × 21√2 × 21√2 - 21 × 21
= 11 × 3 × 21 - 21 × 21
= 693 - 441 = 252 cm2
Therefore, area of shaded region = 252 cm2
Question 16.
A chord of circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:
i) Minor segment
ii) Major segment (use p = 3. 14)
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
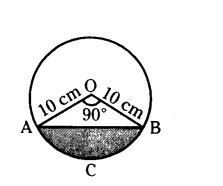
Area of sector OACB = x/360 × πr2
= 90°/360° × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of ∆ AOB = 1/2 × 10 × 10= 50 cm2
Area of the Minor Segment
= Area of sector OACB - Area of ∆ OAB
= 78.5 - 50.0 = 28.5 cm2
Area of Major Segment
= Area of the circle - Area of the Minor Segment
= (3.14 × 10 × 10) - 28.5
= 314 - 28.5 = 285.5 cm2
Question 17.
Find the area of the segment shaded in the figure in which PQ = 12 cm, PR = 5 cm and QR is the diameter of the circle with centre ‘O’. (Take p = 22/7)
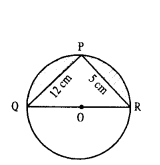
Solution:
To find the area of the segment shaded in the given figure.
Here PQ’ = 12 cm; PR’ = 5 cm; QR’ is diameter
Now PQOR is a semicircle
then angle in a semicircle is 90°
then ∠QPR = 90°
∴ ∆PQR is a right angled triangle
∴ Area of ∆PQR = 1/2 bh
= 1/2 × PQ × PR
= 1/2 × 12 × 5 = 30 cm2 ______ (1)
Now the area of shaded part = area of semicircle - area of ∆PQR
= 1/2 πr2 - 30 cm2 _______ (2)
In ∆PQR, QR2 = PQ2 + PR2 (from Pythagoras theorem)
QR2 = 122 + 52
= 144 + 25 = 169 = 132
QR = 13 then
Radius of the circle (r) = QO = QR/2 = 13/2 = 6.5 cm
then area of semicircle
= 1/2 Pr2
= 1/2 × 22/7 × 13/2 × 13/2 = 66.39 cm2 ________ (3)
Now putting the values of (1) and (3) in (2) we get
Area of shaded part = (66.39 - 30)
= 36.39 cm2.
Question 18.
Ten identical mementos is made by a school to awarding 10 students for first prize winners in games. If each memento is made as shown in figure (shaded portion) its base PQRS is silver plated from the front side at the rate of 20 per square cm. Find the total cost of the silver plating of 10 mementos. (OR = 5cm, RQ = 6cm, PS = 8 cm)
Solution:
Area of right angled triangle
= 1/2 × 13 × 11 = 143/2 = 71.5 cm2
Area of the sector = 90°/360° × 22/7 × 52
= 1/4 × 22/7 × 25
= 19.64 cm2
∴ Area of the shaded portion
= 71.5 - 19.64 = 51.86 cm2
The rate of silver plating per one square cm = Rs. 20
∴ The total cost of the plating of 10 mementos = 51.86 × 10 × 20
= Rs. 10,372
Question 19.
A square ODEF is inscribed in a quadrant OPEQ of circle and OD = 14√2 cm. Aarthi said that "the area of shaded region is 224 cm2." Do you agree ? Give reasons.
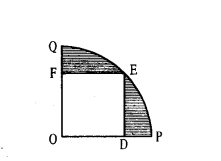
Solution:
Side of the square = OD = 14√2 cm
Length of the diagonal = OE
= √2 (OD)
= √2 (14√2) = 28 cm
Radius of the quadrant OPEQ = r = diagonal of the square ODEF.
Radius of the quadrant OPEQ = r = 28 cm
Area of the quadrant OPEQ = 1/4 pr2
= 1/4 × 22/7 × 28 × 28
= 22 × 28
= 616 cm2
Area of the square ODEF = (OD)2
= (14√2)2 = 196 × 2 = 392 cm2
∴ The area of the shaded region
= Area of the quadrant OPEQ - Area of the square ODEF
= 616 - 392 = 224 cm2
Yes, I agree with Aarthi statement.