10th Lesson Circles Class 10 Important Questions with Solutions
10th Class Maths Circles 1 Mark Important Questions
Question 1.
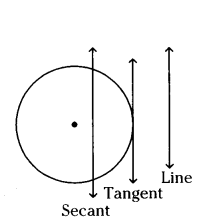
Define secant.
Answer:
A line which intersects a circle in two distinct points is called a secant of the circle.
Question 2.
What is tangent ?
Answer:
A line which touches the circle at only one point is called a tangent of the circle.
Question 3.
How many tangents can a circle have?
Answer:
Infinitely many.
Question 4.
How many tangents can be draw to a circle from an external point ?
Answer:
Two.
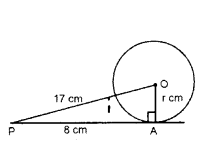
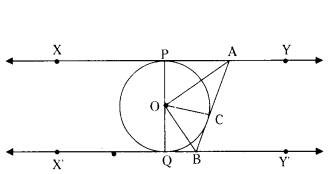
Question 5.
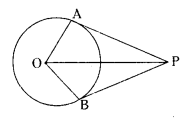
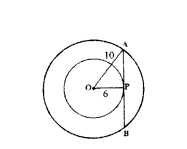
cm. The tangent at a point A on the circle acts the line through O to B such that AB = 15 cm. Find OB.
Solution:
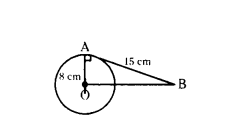
In ∆AOB, ∠OAB = 90°
OA = 8 cm, AB = 15 cm, OB = ?
By Pythagoras theorem,
OB2 = OA2 + AB2 = 82 + 152
OB2 = 64 + 225 = 289 = 172
OB = 17 cm
Question 6.
In the given figure, AB = BC = 10 cm. If AC = 7 cm, then find the length of BP.
Solution:
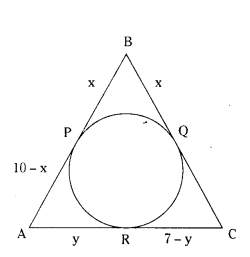
Tangents drawn from an external point of a circle are equal
10 - x = y
x + y = 10 .. (1)
7 - y = 10 - x
x - y = 3 ... (2)
(1) + (2) ⇒ 2x = 13
x = 6.5
∴ BP = 6.5 cm
Question 7.
In the given figure, AB is a tangent to the circle centered at O. If OA = 6 cm and ∠OAB = 30°, then find the radius of the circle.
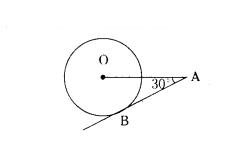
Solution:
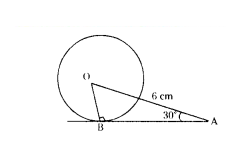
In Right ∆OBA, B = 90°
OB ⊥ AB
sin 30° = OB/OA
1/2 = OB/15
OB = 3 cm.
Question 8.
In the given figure, AC and AB are tangents to a circle centred at O. If ∠COD = 120°, then ∠BAO =
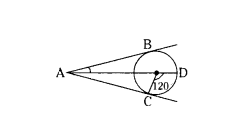
Solution:
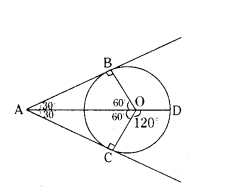
In the figure ∆ABO ≅ ∆ACO
∠CAO = 180 - 90 - 60 = 30°
= 180° - 90° = 30°
∴ ∠CAO = ∠BAO = 30°
Question 9.
In figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ =
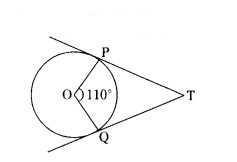
Solution:
In the figure POQT
∠P = ∠Q = 90°
∠POQ = 110°
∠PTQ = 360° - 110° - 90° - 90°
= 360° - 290° = 70°
Question 10.
In the given figure, O is the centre of the circle and PQ is the chord. If the tangent PR at P makes an angle of 50° with PQ, then find the measure of ∠POQ
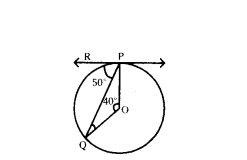
Solution:
∆POQ is an Isosceles triangle
∠OPR = 90° as OP ⊥ PR
∠OPQ = 90° - 50° = 40°
∴ ∠OQP = 40 = ∠OPQ
∴ ∠POQ = 180° - 40° - 40° = 100°
Question 11.
Find the length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centtre.
Solution:
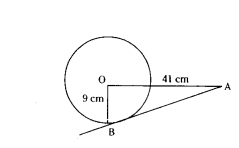
In the figure 412 = 92 + AB2
1681 - 81 = AB2 ⇒ AB2 = 1600
AB = 40 cm
Question 12.
A circle is of radius 3 cm. Find the distance between two of its parallel tangents.
Solution:
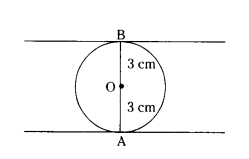
AO + BO = 3 + 3 = 6 cm
Question 13.
In Fig. ∆ABC is circumscribing a circle, the length of BC is ....... cm.
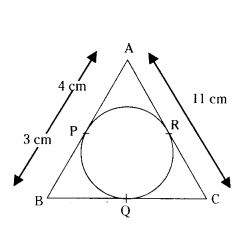
Solution:
The lengths of tangents drawn from an external point of a circle are equal.
PB = BQ = 3 cm
AR = PA = 4 cm
CR= 11 - 4 = 7 cm
∴ QC = 7 cm
BC = BQ + QC
= 3 + 7 = 10 cm
Question 14.
The length of the tangent from an external point A to a circle of radius 3 cm, is 4 cm. Find the distance of A from the center of the circle.
Solution:
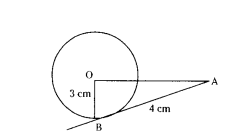
OB ⊥ AB
OA2 = 32 + 42
OA2 = 25
OA = √25 = 5 cm
Question 15.
Assertion (A) : A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R) : The lengths of tangents drawn from an external point to a circle are equal.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Solution:
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
Question 16.
In the given circle in fig., find the number of tangents parallel to tangent PQ.
Solution:
1 tangent
Question 17.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any (joint on the circle. Then find the measure of ∠AQB.
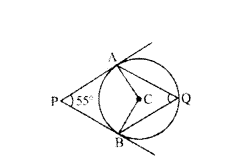
Solution:
∠AQB = 180° - 55° = 125°
Question 18.
In the figure, if PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB =
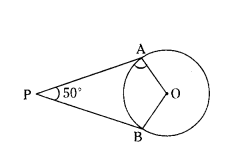
Solution:
∠AOB = 180° - 50° = 130°
Let ∠OAB = ∠OBA = x°
x° + x° + 130° = 180°
2x° = 180° - 130°
2x = 50°
x = 50/2
x = 25°
∠OAB = 25°
Question 19.
In the given figure, find the perimeter of ∆ABC.
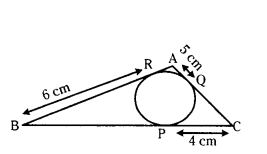
Solution:
The length of tangents drawn from an external point of a circle an equal.
BR = BP = 6 cm
AQ = AR = 5 cm
PC = QC = 4 cm
Perimeter of ∆ABC = 10 + 9 + 11 =30 cm
Question 20.
In the given figure, BC and BD are tangents to the circle with centre O and radius 9 cm. If OB = 15 cm, then find the length (BC + BD).
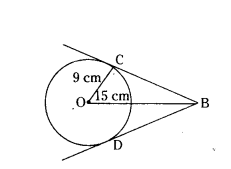
Solution:
In ∆BCO, ∠OCB = 90°
152 = 92 + BC
225 - 81 = BC2
144 = BC2
BC = 12 cm
The lengths of tangents drawn from an external point are equal
BC = BD = 12 cm
BC + BD = 12 + 12 = 24 cm.
Question 21.
Assertion (A) : A tangent to a circle is perpendicular to the radius through the point of contact.
Reason (R) : The lengths of tangents drawn from the external point to a circle are equal.
Choose the correct answer.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Answer:
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Question 22.
Statement p: If a circle touches all four Sides of a quadrilateral ABCD, then AB + CD = BC + AD.
Statement q : A parallelogram circum-scribing a circle is a rhombus.
Choose the correct answer.
A) p true, q false
B) p false, q true
C) p true, q true
D) p false, q false
Answer:
C) p true, q true
Question 23.
In the figure, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm then PS = ........ cm.
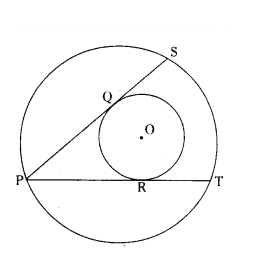
Solution:
The lengths of tangents drawn from the external point of a circle are equal
PQ = PR = 5 cm
OQ ⊥ PS
∴ PQ = QS
∴ PQ = QS = 5 cm
PS = PQ + QS
= 5 + 5 = 10 cm
Question 24.
In the figure PA and PB are tangents to a circle with centre ‘O’. If ∠AOB = 120° then ∠OPA = .......
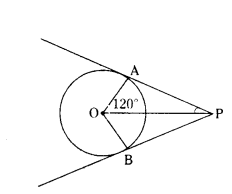
Solution:
In the figure, ∠AOB = 120°
∠AOP = ∠BOP = 120/2 = 60°
OA⊥PA
∠OAP = 90°
∴ ∠OPA = 180° - 60° - 90°
= 180° - 150° = 30°
Question 25.
Assertion (A) : In the given figure PA = PB
Reason (R) : Area of Circle = πr
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Answer:
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
Question 26.
Assertion (A) : In the figure AB = 14 cm
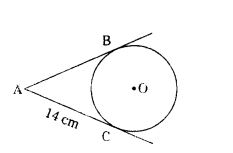
Reason (R) : The lengths of tangents drawn from an external point of a circle are equal.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Answer:
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
Question 27.
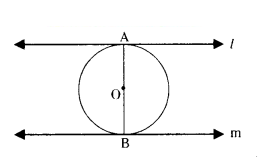
Assertion (A) : In the figure l‖ m
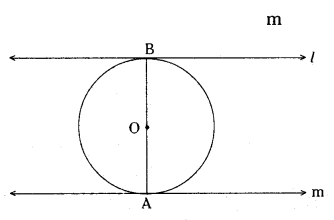
Reason (R) : The tangents drawn at the
end point of diameter of a circle are parallel.
A) Both Assertion (A) and Reason (R) are true and Reason, (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Solution:
A) Both Assertion (A) and Reason (R) are true and Reason, (R) is the correct explanation of Assertion (A).
Question 28.
Assertion (A) : In the figure, x = 50°.
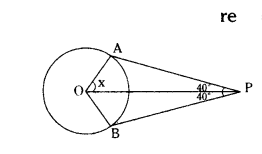
Reason (R) : Cyclic parallelogram is triangle.
A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
B) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
C) Assertion (A) is true but Reason (R) is false.
D) Assertion (A) is false but Reason (R) is true.
Solution:
C) Assertion (A) is true but Reason (R) is false.
Question 29.
For a circle which is inscribed in a AABC having sides 8 cm, 10 cm and 12 cm. Then match the column.
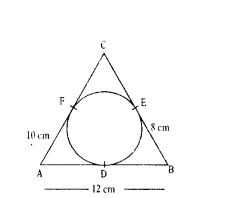
A) AD
B) BE
C) CF
D) AD/AF
i) 1
ii) 7
iii) 5
iv) 3
Answer:
A - (ii), B - (iii), C - (iv), D - (i)
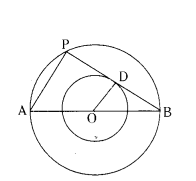
Question 30.
If two tangents PA and PB are drawn to a circle with centre ‘O’ from an external point ‘P’ (figure), then match the column.
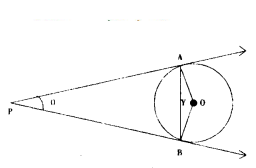
A) ∠PAB
B) ∠OAP
C) ∠OAB
D) ∠AOB
i) 90°
ii) θ/2
iii) 90 - θ/2
iv) 180° - θ
Answer:
A - (iii), B - (i), C - (ii), D - (iv)
Question 31.
If AB is a chord of length 6 cm, of a circle of radius 5 cm, the tangents at A and B intersects at a point X, then match the column.
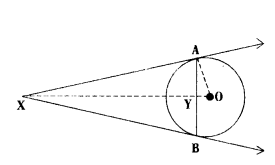
A) AY
B) OY
C) XA
D) OA
i) 4 cm
ii) 3.75cm
iii) 5 cm
iv) 3 cm
Answer:
A - (iv), B - (i), C - (ii), D
Question 32.
The length of the minutes hand of a clock is 7 cm then how much distance does it cover in one hour ?
Answer:
44 cm
Question 33.
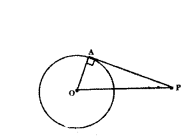
How many tangents can be drawn on a circle from a point outside the circle?
Solution:
Only two tangents can be drawn from an external point to the circle i.e., PA, PB are the two tangents to the circle.
Question 34.
What is the angle between the radius and tangent at the point of contact ?
Answer:
90°
Question 35.
Statement p : If a circle touches all four sides of a quadrilateral ABCD, then AB + CD = BC + AD.
Statement q: A parallelogram circumscribing a circle is a rhombus.
A) p true, q false
B) p false, q true
C) p true, q true
D) p false, q false
Answer:
C) p true, q true
Question 36.
The number of common tangents can be drawn to two concentric circles is .......
Solution:
0 (zero).
Question 37.
Statement ‘p’ : A tangent to a circle intersects it in one point.
Statement ‘q’ : We can draw infinite tangents to a given circle.
Choose the correct answer :
A) Statement ‘p’ and ‘q’ both are true.
B) Statement ‘p’ is true, ‘q’ is false.
C) Statement ‘p’ is false, ‘q’ is true.
D) Statement ‘p’ and ‘q’ both are false.
Answer:
A) Statement ‘p’ and ‘q’ both are true.
10th Class Maths Circles 2 Mark Important Questions
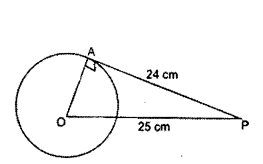
Question 1.
If the tangent at a (mint P to a circle with centre O cuts a line through O at Q such that PQ = 24 cm and OQ = 25 cm. Find the radius of the circle.
Solution:
In ∆POQ, ∠OPQ = 90°
OQ = 25 cm, PQ = 24 cm, OP = ?
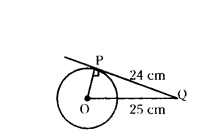
By Pythagoras theorem,
OQ2 - OP2 + PQ2
OP2 = OQ2 - PQ2 = 252 - 242
OP2 = 72
∴ OP = 7 cm
Therefore, radius of the circle OP = 7 cm.
Question 2.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q. So that OQ = 13 cm. Find the length of PQ.
Solution:
In ∆OPQ, ∠OPQ = 90°
OP = 5 cm, OQ = 13 cm, PQ = ?
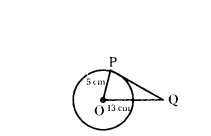
By Pythagoras theorem,
OP2 + PQ2 = OQ2
PQ2 - OQ2 - OP2
= 132 - 52 = 169 - 25 = 144
PQ2 - 122
∴ PQ = 12 cm
Question 3.
In the given figure, PQ is a chord of the circle centered at O. PT is a tangent to the circle at P. If ∠QPT = 55°, then find ∠PRQ.
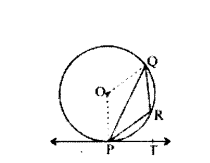
Solution:
Given PQ is a chord.
‘O’ is centre of circle
PT is a tangent
∠QPT = 55°
∠QPT + ∠OPT = 90°
∠OPT = 90° - 55° - 35°
In ∆POQ
∠POQ = 180° - ∠OPQ - ∠PQO
= 180° - 35° - 35° = 180° - 70° = 110°
Major curve ∠POQ = 360° -110° = 250°
∠QRP = 1/2 × 250 = 125°
∴ ∠PRQ = 125°
Question 4.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution:
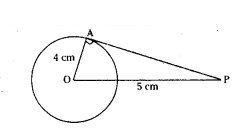
In the figure
‘O’ is centre of circle
OA = 4 cm
OP = 5 cm
52 = 42 + PA2
25 - 16 = PA2
PA2 = 9
PA = √ 9 = 3 cm
∴ The length of tangent = 3 cm
Question 5.
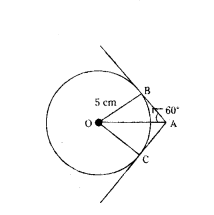
In the given figure, tangents AB and AC are drawn to a circle centred at O. If ∠OAB = 60° and OB = 5 cm, find lengths OA and AC.
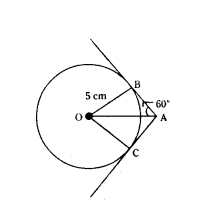
Solution:
In the figure,
AB and AC are tangents
AB = AC
∠OAB = 60°
OB = 5 cm
‘O’ is centre of circle.
OC = 5 cm
In Right ∆OBA, ∠B = 90°
sin 60° = 5/OA
√3/2 = 5/OA
√3 OA = 10
OA = 10/√3 cm
tan 60° = 5/OA
√3 = 5/OA
AB = 5/√3
AB = AC
∴ AC = 5/√3 × √3/√3 = 5/3 √3 √3 cm
∴ OA = 10/√3 × √3/√3 = 10√3/3 cm
AC = 5/3 √3 cm
Question 6.
In fig. AB is diameter of a circle centred at O. BC is tangent to the circle at B. if OP bisects the chord AD and ∠AOP = 60°, then find ∠C.
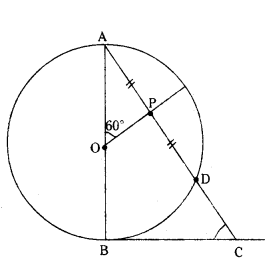
Solution:
‘O’ is centre of circle
BC is tangent
OP bisects chord AD.
then OP ⊥ AD
∴ AP = PD
∠AOP = 60°
∠APO = 90°
∴ ∠BAC = 180° -60° -90°
= 180° - 150° = 30°
OB ⊥ BC
∠OBC = 90°
In ∆ABC
∠A + ∠B + ∠C = 180°
30° + 90° + ∠C = 180°
120° + ∠C = 180°
∠C = 180° -120°
∠C = 60°
C = 60°
Question 7.
In fig. XAY is a tangent to the circle centred at O. If ∠ABO = 40°, then find ∠BAY and ∠AOB.
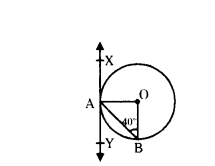
Solution:
Given XAY is a tangent to the circle
‘O’ is centre of circle.
∠ABO = 40°
OA = OB
∴ ∠OAB = ∠OBA = 40°
∠AOB = 180°- 40°- 40°
= 180° - 80° = 100°
∠AOB = 100°
OA⊥XY
∴ ∠OAY = 90°
∠OAB + ∠BAY = 90°
40° + ∠BAY = 90°
∠BAY = 90°-40°
∠BAY = 50°
∴ ∠BAY = 50°
Question 8.
Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
Solution:
Given TP and TQ are two tangents
‘O’ is centre of circle
we have to prove ∠PTQ = 2∠OPQ
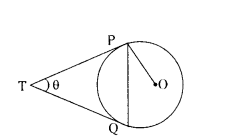
We have TP = TQ
∴ TPQ is an Isosceles Triangle
∠TPQ = ∠TQP
= 1/2 (180 - θ) = 90 - θ/2
∠OPT = 90°
∠OPQ = ∠OPT - ∠TPQ
= 90° - (90° - θ/2 ) = 1/2 θ = 1/2 ∠PTQ
∴ ∠PTQ = 2∠OPQ.
Question 9.
The distance between two tangents parallel to each other of a circle is 13 cm. Find the radius of the circle.
Solution:
Distance between parallel tangents = 13 cm
∴ Diameter =13 cm
Radius = 13/2 = 6.5 cm
Question 10.
In the given figure, PA is a tangent to the circle drawn from the external point P and PBC is the secant to the circle with BC as diameter. If ∠AOC = 130°, then find the measure of ∠APB, where O is the centre of the circle.
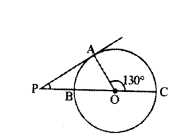
Solution:
In the figure ∠AOC = 130°
‘O’ is centre of circle
∠AOP = 180° - 130° = 50°
OA ⊥ PA
∠OAP = 90°
In ∆OAP,
∠OAP + ∠AOP + ∠APO = 180°
90° + 50° + ∠APO = 180°
∠APO = 180°-140°
∠APO = 40°
∴ ∠APB = 40°
Question 11.
In Fig. perimeter of ∆PQR p is 20 cm. Find the length of tangent PA.
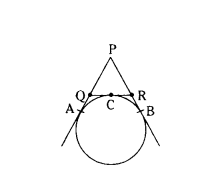
Solution:
Given perimeter of ∆PQR = 20 cm
PQ + QR + PR = 20 cm
PQ + (QC + CR) + PR = 20
The lengths of tangents drawn from external point of circle are equal.
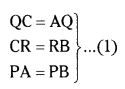
(PQ + QA) + RB + PR ) = 20 (by (1))
PA + PB = 20
PA + PA = 20 (by (1))
2PA = 20
PA = 10 cm
Question 12.
In Fig. BC is tangent to the circle at point B of circle centered at O. BD is a chord of the circle so that ∠BAD = 55°. Find m ∠DBC.
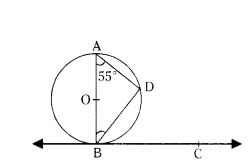
Solution:
Given BC is tangent to the circle.
Let point B of circle.
O’ is a centre of circle BD is a chord.
∠BAD = 55°
Angle in a semi circle is 90°
∠ADB = 90°
∠DBA = 180° - 90° - 55°
= 180 - 145 = 35°
∴ ∠DBC = 90° - 35° = 55°
∴ ∠DBC = 55°
Question 13.
XY and MN are the tangents drawn at the end points of the diameter DE of the circle with centre O. Prove that XY ‖ MN.
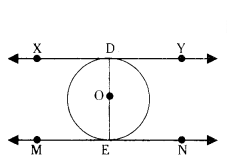
Solution:
Given XY and MN are two tangents drawn at the end points of the diameter DE.
O is the centre of the circle.
We have to prove XY ‖ MN .
We have
OE ⊥ MN
OD ⊥ XY
∴ ∠OEM = ∠OEN = 90°
∠ODX = ∠ODY = 90°
Also ∠ODY + ∠OEN = 90° + 90° = 180°
Sum of interior angles on the same side of the transversal is 180°.
∴ XY ‖ MN.
Question 14.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other is a secant to the circle.
Solution:
Question 15.
PA is the tangent drawn to a circle of whose centre is ‘O’, OA is the radius and P is the external point of the circle. If PA = 24 cm, OP = 25 cm., then find its radius.
Solution:
Given PA = 24 cm, OP = 25 cm
We have OP2 = OA2 + PA2
⇒ (25)2 = OA2 + (24)2
⇒ 625 = OA2 + 576
⇒ OA2 = 49
⇒ OA = 7 cm
Question 16.
Find the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
Solution:
Radius of the circle = 5 cm
Length of the tangent = x cm
Distance between centre to point be = 13 cm
132 = 52 + x2
x2 = 169 - 25 = 144 ⇒ x = 12 cm
Now, in ∆AOP,
∠POA + ∠OPA + ∠A = 180°
⇒ ∠POA + 40° + 90° = 180°
⇒ ∠POA = 50°
Question 17.
Find the length of the tangent from a point, which is 9.1 cm away frbm the centre of the circle, whose radius is 8.4 cm.
Solution:
Radius of the circle = r = 8.4 cm
Distance between centre to the point = d = 9.1 cm.
Length of the tangent = l = √d2-r2
= √(9.1)2-(8.4)2
= √82.81?70.56
= √12.25 = 3.5 cm.
∴ Length of the tangent = 3.5 cm.
Question 18.
"The length of the tangent from an external point ‘P’ to a circle with centre ‘O’ is always less than OP." Is this statement true ? Give reasons.
Solution:
∆ OAP is right triangle.
OP is hypotenuse. AP is tangent to the circle at A.
∴ OP > AP (v Hypotenuse is longest side)
OP > length of the tangent
∴ Given statement is true.
Question 19.
The length of the tangent to a circle from a point 17 cm from its centre is 8 cm. Find the radius of the circle.
Solution:
Let PA is the length of the tangent PA = 8 cm
The distance of the external point from the centre OP = 17cm
Radius = OA = r cm.
∴ 172 = r2 + 82
⇒ r2 = 172 - 82 = 289 - 64 = 225
⇒ r = √225 = 15 cm
Question 20.
A point P is 25 cm from the centre O of the circle. The length of the tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
Solution:
From right angled ∆ AOP
OP2 = OA2 + AP2
(25)2 = OA2 + (24)2
625 = OA2 + 576
OA2 = 625 - 576 = 49 = 72
OA = 7 cm
∴ The radius of the circle is 7 cm.
Question 21.
Find the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
Solution:
Radius of the circle = 5 cm
Length of the tangent = x cm
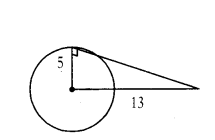
Distance between centre to point be
= 13 cm
132 = 52 + x2
x2 = 169 - 25 = 144 ⇒ x = 12 cm
Question 22.
In the given figure, ‘O’ is the centre of a circle, OQ is the radius and OQ = 5 cm. The length of the tangent drawn from external point to the circle PQ =12 cm, then find the distance between the points ‘O’ and ‘P’.
Solution:
The radius is perpendicular to the tangent at the point of contact i.e. ∠OQP = 90°
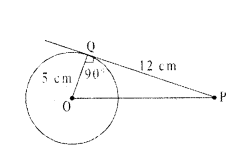
∆OQP is a Right angled triangle
⇒ (OP)2 = (OQ)2 + (PQ)2
⇒ OP = √(OQ)2 + (PQ)22 = √(5)2+(12)2
⇒ OP = √25+144 = √169 = 13 cm
∴ The distance between two points O and P = 13 cm
Question 23.
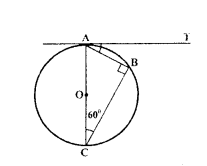
AOB is the diameter of a circle with centre ‘O’ and AC is a tangent to the circle at A. If ∠BOC = 130°, then find ∠ACO.
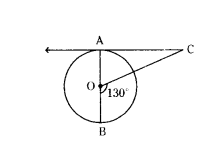
Solution:
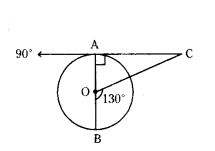
Given that
AOB is diame’ter and centre is O
AC is a tangent
∠BOC =130° and point of contact at A.
We know that
The angle at point of contacat is 90°
The angle of straight line is 180°
∠AOC + ∠BOC = 180°
∠AOC + 130° = 180°
∠AOC = 180° - 130°
∠AOC = 50°
In a triangle
The sum of angles = 180°
∠AOC + ZOAC + ∠ACO = 180°
∠ACO + 90° + 50° = 180°
∠ACO = 180° - 140°
∠ACO = 40°
So, the angle ∠ACO is 40°
10th Class Maths Circles 4 Mark Important Questions
Question 1.
From an external point P, two tangents PA and PB are drawn to the circle with centre O. Prove that OP is the perpendicular bisector of AB.
Solution:
Given O is the centre of circle.
AP and PB are tangents drawn to a circle from P that is AP = BP and AB is the chord which meets OP at C.
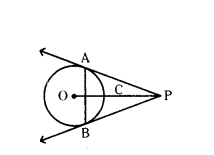
In ∆APC and ∆BPC,
PA = PB (Side)
∠APC = ∠BPC (Angle)
PC = PC (Side)
by S-A-S similarity ∆APC ~ ∆BCP
By CPCT, ∠ACP = ∠BCP
∠ACP + ∠BCP = 180°
Therefore, ∠ACP = ∠BCP = 180°/2 = 90°
Hence, OP⊥AB
So, OP is the perpendicular bisector of AB.
Question 2.
O is the centre of the circle in the given figure. PA and PB are tangents. Show that AOBP is a cyclic quadrilateral.
Solution:
In the figure OA⊥AB and OB⊥BP.
Radius is perpendicular to the tangent at its point of contact.
∠OAP = ∠OBP = 90°
So, ∠OAP +∠OBP = 180°
In quadrilateral OAPB,
∠OAP + ∠APB + ∠OBP + ∠AOB = 360°
(∠OAP + ∠OBP) + ∠APB + ZAOB = 360°
180° + ∠APB + ∠AOB = 360°
∠APB + ∠AOB = 360° - 180° = 180°
So, the quadrilateral OAPB is cyclic.
Question 3.
If AB, AC, PQ are tangents to the circle and AB = 5 cm in the given figure. Find the perimeter of the triangle.
Solution:
Given AB, AC, PQ are tangents.
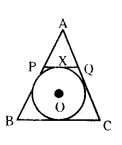
AB = 5 cm
Tangents drawn to a circle for the external point are equal.
That is AB = AC, BP = PX, QC = XQ
Perimeter of ∆APQ
= AP + AQ + PQ
= AP + AQ + PX + XQ
= (AP + PX) + (AQ + XQ)
= AB + AC
But, AB = AC = 5 cm
Perimeter = AB + AC = 5 + 5 = 10 cm
Question 4.
In the given figure, ∆ABC is a right triangle, right angle at B such that BC = 6 cm and AB = 8 cm. Find the radius of the in circle.
Solution:
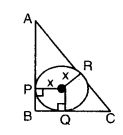
Given in ∆ABC, ∠B = 90°
AB = 8 cm, BC = 6 cm
Let radius of circle be x cm
So, OPBQ is a square
That is OP= OQ = PB = BQ = x cm
Tangents drawn to the circle from an external point are equal.
That is AP = AR, PPB = BQ = x, CQ = CR
AR = AP = AB - BP = 8 - x
CR = CQ = BC - BQ = 6 - x
AR + CR = AC = 8 - x + 6 - x = 14 - 2x
by Pythagoras theorem,
AC2 = AB2 + BC2
(14 - 2x)2 = 82 + 62 = 102
14 - 2x = 10 ⇒ -2x = 10 - 14
-2x = -4
x = 4/2 = 2 cm
∴ Radius of the circle is 2 cm.
Question 5.
Two circles touch externally at a point P. From a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and R respectively. Prove that TQ = TR.
Solution:
Given TP, TQ and TR are tangents to the two externally touching circles.
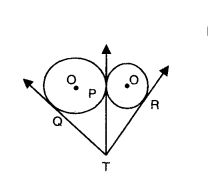
Tangents drawn to the circle from an external point are equal.
That is TP = TQ → (1)
TP = TR → (2)
From (1) and (2) TQ = TR.
Question 6.
In the given figure, AP and AQ are tangents from A to the circle with centre O. B is a point on the circle, then prove that AX + XB = AY + YB.
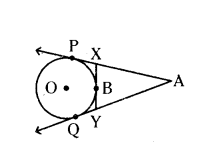
Solution:
Given in the figure, AP, AQ and XY are tangents drawn to the circle. Tangents drawn from external point are equal.
That is, AP = AQ
XP = XB
YQ = YB
Now, AP = AQ
AX + XP = AY + YQ
AX + XjB = AY + YB (∵ XP = XB, YQ = YB)
Question 7.
In the given figure, a circle touches all the four sides of a quadrilateral ABCD with AB = 6 cm, BC = 7 cm and CD = 4 cm. Find AD.
Solution:
Given circle touches all the four sides of a quadrilateral AB, BC, CD and DA at P, Q, R and S respectively.
We know that if a circle touches all the four sides of a quadrilateral ABCD then AB + CD = BC + AD.
Given AB = 6 cm, BC = 7 cm and CD = 4cm
6 + 4 = 7 + AD
10 - 7 = AD
∴ AD = 3 cm
Question 8.
In the given figure CP and CQ are tangents to a circle with centre O. AB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm then find the length of BR.
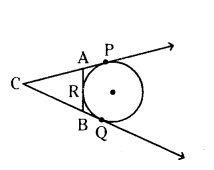
Solution:
Given, CP, CQ and AB are tangents to the circle with centre O. CP = 11 cm, BC = 7 cm.
We know that, tangents drawn from external point C are equal.
That is, AP = AR, BQ = BR and CQ = CP
BC + BQ = CP
7 + BQ = 11
BQ = 11 - 7 = 4cm
BQ = BR = 4 cm
Therefore, BR = 4 cm
Question 9.
In the given figure ∆ABC is circum-scribing a circle. Find the length of BC.
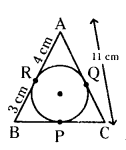
Solution:
Given ∆ABC is circumscribing a circle.
AC = 11 cm, AR = 4 cm, BR = 3 cm
We know that tangents drawn from an external point are equal.
That is AR = AQ, BP = BR, CP = CQ
AC = AQ + CQ = 11 cm
AR + CQ = 11 cm (∵ AQ = AR)
4 + CQ = 11
CQ = 11 - 4 = 7 cm
But, CQ = CP = 7 cm
and BP = 3 cm
BC = BP + CP = 3 cm + 7 cm = 10 cm
Therefore, BC = 10 cm
Question 10.
Prove that the angle between the two tangents drawn from an external to circle is supplementary to the angle subtended by the line joining the points of contact at the centre.
Solution:
Let ‘O’ be the centre of circle
P is the external point
AB is the chord
OA = OB = radius
OA⊥PA and OB⊥PB
∴ ∠OBD = 90°; ∠OAP = 90°
In the Quadrilateral OAPB,
Sum of all interior angles = 360°
∠OAP + ∠OBP + ∠BOA + ∠APB = 360°
90° + 90° + ∠BOA + ∠APB - 360°
∠BOA + ∠APB = 180°
∴ The angle between the two tangents drawn from an external point to a circle supplementary to the angle subtended by the line segment.
Question 11.
ABC is an isosceles triangle with AB = AC, circumscribed about a circle. Prove that BC is bisected at E.
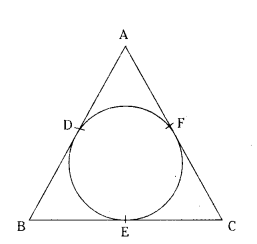
Solution:
We know that,
The lengths of tangents drawn from an external point of a circle are equal.
In Isosceles triangle ABC, AB = AC.
AB - AF = AC - AF
AB - AD = AC - AD
BD = CF
BE = CF [by (1)]
∴ BC is bisected at the point of contact.
Question 12.
In the given figure, the radii of two concentric circles are 13 cm and 8 cm. AB is diameter of the bigger circle. BD is the tangent to the smaller circle touching it at D. Find the length AD.
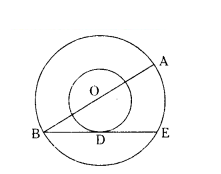
Solution:
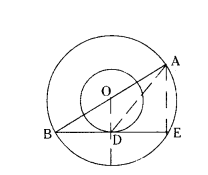
Join OD and AE
∠ODB = 90° (OD⊥BE)
∠AEB = 90° (angle in semi circle)
OD ‖ AE (corresponding angles)
AE = 2 × OD
AE = 2 × 8 = 16 cm
In Right ∆ODB,
BD2 = 132 - 82 = 169 - 64 = 105
BD = √105 cm
DE = √105 cm
In Right ∆AED,
AD2 = AE2 + DE2
= 162 + (√105)2 = 256 + 105 = 361
AD = √361
AD = 19 cm
Question 13.
P & Q are centres of circles of radii 9 cm and 2 cm respectively. PQ = 17 cm. R is the centre of the circle of radius x cm, which touches the above circle externally. Given that angle PRQ is 90°. Write an equation in x and solve it.
Solution:
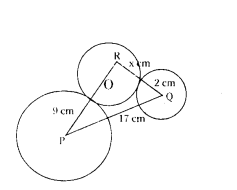
In Right APQR, by pythagoras theorem
PQ2 = PR2 + QR2
172 = (x + 9)2 + (x + 2)2 [Aftering solving]
x2 + 11x - 102 = 0
x2 + 17x - 6x - 102 = 0
x(x + 17) - 6(x + 17) = 0
(x - 6) (x + 17) = 0
x = 6 or x = -17
x = 6 cm only
∴ x = 6 cm
Question 14.
If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that
AQ = 1/2 (BC + CA + AB).
Solution:
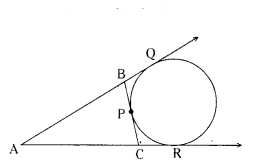
Given : The circle touches the side BC of ∆ABC at P.
The circle touches the extended sides
AB and AC of the triangles at Q and R.
To prove : AQ = 1/2 (BC + CA + AB)
Proof : We know that, "the lengths of tangents drawn from an external point of a circle are equal".
BP = BQ ... (1)
CP = CR ... (2)
AQ = AR .. (3)
Perimeter of ∆ABC = AB + BC + AC
From the figure
BC = BP + PC
AB + BC + AC = AB + (BP + PC) + AC
= AB + BQ + CR + AC
From the figrue
AB + BQ = AQ
CR + AC = AR
BQ + CR = BC
AB + BC + AC = AQ + AR
∴ AB + BC + AC = AQ + AQ
2AQ = AB + BC + AC
∴ AQ = 1/2 [AB + BC + AC]
Question 15.
In the figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.

Solution:
In the figure join OT.
OT meets PQ at the point R
∆TPQ is an isosceles .
TO is the angle bisector of ∠PTO
We have, the lengths of tangents drawn from external point of a circle are equal.
∴ TP = TQ
OT⊥PQ
OT bisects PQ
PR = RQ = 4 cm
OR = √OP2?PR2
OR = √52?42 = 3cm
∠TPR + ∠RPO = 90° (∵ ∠TPO = 90°)
∠TPR + ∠PTR = 90°
∠RPO = ∠PTR
∆TRP ~ ∆RPO (AA rule)
TP/PO = RP/RO
⇒ TP/15 = 4/3
TP = 20/3 cm
Question 16.
In given figure XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that
∠AOB = 90°
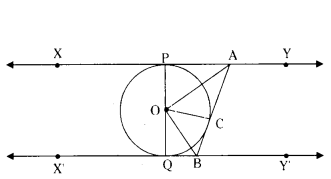
Solution:
O is centre of circle
Join OC
In ∆OPA and ∆OCA
OP = OC (radii)
AP = AC (Tangents from A)
AO = BO (Common side)
by SSS congruence rule
∆OPA ≅ ∠OCA
by CPCT ∴ ∠POA = ∠COA .. (1)
similarly ∠QOB = ∠OCB
∠QOB = ∠COB .... (2)
here POQ is a diameter of circle
∴ ∠POA + ∠COA +∠COB + ∠QOB = 180°
by (1) & (2)
2∠COA + 2∠COB = 180°
∠COA + ∠COB = 90°
∠AOB = 90°
Question 17.
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP.
Solution:
In the figure
‘O’ is centre of circle
OD⊥BD
∴ ∠ODB = 90° = ∠ODP
Let P be a point on bigger circle.
∴ ∠APB = 90°
In ∆ABP and ∆OBD
∠APB = ∠ODB = 90°
∠ABP = ∠ODB (Common)
∆ABP ~ ∆OBD (AA similarly)
∴ AP/OD = AB/OB
AP/8 = 26/13
AP = 2 × 8
AP = 16 cm
Question 18.
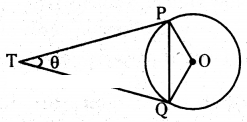
If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at angle of 80°, then find the measured of ∠POA.
Solution:
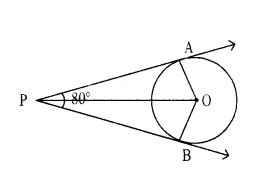
Between ∆AOP and ∆BOP
∠OAP = ∠OBP = 90° (∵ tangent and line from origin meet at 90° to each other)
OA = OB = radius of the circle = r (say) and OP is the common side
Hence, we can say ∆AOP = ∆BOP
Therefore, we can say
∠OPA = ∠OPB = 1/2 (∠APB)
= 1/2 (80°) = 40°
(∵ given that tangents PA and PB are inclined to each other by 80°)
Now, in ∆AOP,
∠POA + ∠OPA + ∠A = 180°
⇒ ∠POA + 40° + 90° = 180°
⇒ ∠POA = 50°
Question 19.
Prove that "in two concentric circles, a chord of the bigger circle, that touches the smaller circle is bisected at the point of contact with the smaller circle."
Solution:
Proof : We are given two concentric circles C1 and C2 with centre O and a
chord AB of the larger circle C1, touching the smaller circle C, at the point P
(see figure) we need to prove that AP = PB. Join OP.
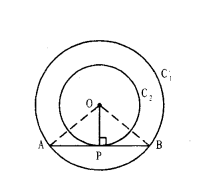
Then AB is a tangent to the circle C2 at P and OP is its radius.
Therefore, by Theorem 9.1
i. e., OP⊥AB
Now, ∆OAP and ∆OBP are congruent. This means AP = PB. Therefore, OP is . the bisector of the chord AB, as the perpendicular from the centre bisects the chord.
Question 20.
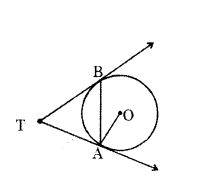
From an external point, two tangents are drawn to a circle. A line joining the external point and the center of the circle bisects the angle between the tangents. Is this true or not ? Justify your answer.
Solution:
Proof : Let PQ and PR be two tangents drawn from a point P outside of the circle with centre O. Join OQ and OR, triangle OQP and ORP are congruent because we know that,
∠OQP = ∠ORP - 90° (Theorem 9.1) i.e.,
OP⊥XY
OQ = OR (Radii)
OP is common.
This means ∠OPQ = ∠OPR (CPCT)
Therefore, OP is the angle bisector of ∠QPR.
Hence, the centre lies on the bisector of the angle between the two tangents.
Question 21.
AB is a chord of the circle and AOC is its diameter, such that ∠ACB = 60°. If AT is the tangent to the circle at the point A, then find the measure of ∠BAT.
Solution:
According to the data ∠ACB = 60°
AOC = diameter; AB = chord
AT is a tangent to the circle at A.
∴ ∠ACB = 90° (∵ semi-circle angle)
∠BAC + ∠ACB - 90°
∠BAC + 60° - 90°
⇒ ∠BAC = 30°
AT⊥AOC, ∠CAT = 90°
∠BAC + ∠BAT = 90°
30° + ∠BAT = 90°
⇒ ∠BAT = 60°
Question 22.
In the given figure, TA and TB are tangents to the circle with centre ‘O’. If ∠ATB = 80°, then find the measure of ∠ABT.
Solution:
In ∆TAB
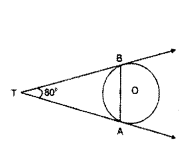
TA = TB (v Length of the tangents drawn from the external point are equal)
⇒ ∠TBA = ∠TAB (∵ Angles opposite to the equal sides are equal)
⇒ Let ∠TBA = ∠TAB = x°
80° + x° + x° = 180° (∵ Sum of the angles in a triangle is 180°)
2x° = 180° - 80° = 100°
x° = 50°
∴ ∠ABT = 50°
Question 23.
In the given figure AB, AC and PQ are tangents to a circle and AB = 6 cm. Find the perimeter of ∆APQ.
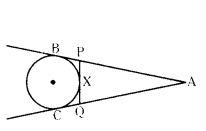
Solution:
We know that tangents drawn from an external point to a circle are equal in length.
∴ AB = AC
AP + PB = AQ + QC
AP + PX = AQ + QX (∵ PX = BP and QX = QC)
AP + PX = AQ + QX = 6 cm
Now, Perimeter of
∆APQ = AP + PQ + AQ = (AP + PX) + (QX + AQ)
= 64 + 6 = 12 cm
∴ Perimeter of ∆APQ = 12 cm
Question 24.
A circle of radius 3 cm is inscribed in a triangle ABC and AF = 5 cm, BF = 3 cm as shown in the figure.
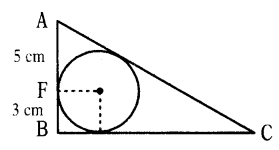
Somu said that the measure of the side AC is 17 cm. Do you agree ? Give reasons.
Solution:
AB = 8 cm, AD = 5 cm, BE = 3 cm
Let CD = CE = x
AC = 5 + x, BC = 3 + x
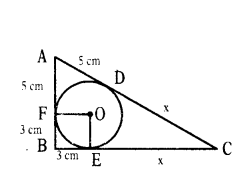
Since OE = OF = radius and
OF ⊥ AB, OE ⊥ BC
∴ AB ⊥ BC
From ∆ABC
AC2 = AB2 + BC2
(5 + x)2 = (8)2 + (3 + x)2 (∵ a2 - b2 = (a + b) (a - b))
(8 + 2x)2 = 64
8 + 2x = 32
⇒ 2x = 24
⇒ x = 12
∴ AC = 5 + x = 5 + 12 = 17 cm
Question 25.
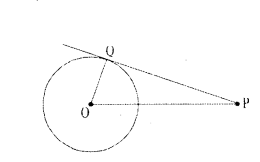
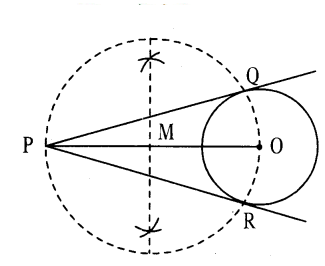
Draw the tangent to a given circle with centre O from a point R outside the circle. How many tangents can be drawn to the circle from that point ?
Solution:
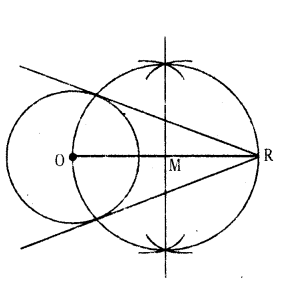
Steps of construction :
- Draw a circle with centre ‘O’,
- Take a point P outside the circle. Join OP.
- Draw the perpendicular bisector to OP which bisects it at M.
- Taking M as centre and PM or MO as radius draw a circle. Let the circle intersects the given circle at A and B.
- Join P to A and B.
- PA and PB are the required tangents.
- Only two tangents can be drawn.
(OR)
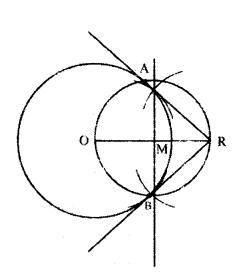
10th Class Maths Circles 8 Mark Important Questions
Question 1.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Solution:
Given PQ = 8 cm, OP = OQ = 5 cm
Let TP = TQ = a cm
and TR = b cm
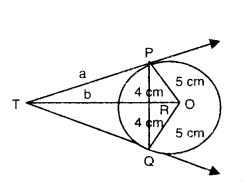
OT is perpendicular bisector of PQ.
i.e., OR = QR = PQ/15 = √8/2 = 4 cm
In ∆OPR,
OP = OR2 + PR2
OR2 = OP2 - PR2 = 52 - 42
OR2 = 25 - 16 = 9 = 32
OR = 3 cm
In ∆TPR, TP2 = TR2 + PR2 → (1)
and in ∆OPT, OT2 = TP2 + OP2 → (2)
Put (1) in (2)
OT2 = (TR2 + PR2) + OP2
(b + 3)2 = b2 + 42 + 52

Question 2.
In the given figure if AB = AC prove that BE = EC.
Solution:
Given in ∆ABC, AB = AC which circumscribed a circle.
Tangents drawn from an external point are equal.

(AD + BD) + CE = (AF + CF) + BE
AB + CE = AC + BE
M + CE = M + BE (∵ AB = AC)
CE = BE (or) BE - CE
So, point of contact E can bisect the base BC.
Question 3.
In the figure, the in circle of AABC touches the sides BC, CA and AB at D, E and F respectively. Show that AF + BD + CE - AE + BF + CD = 1/2 (Perimeter of ∆ABC).
Solution:
Tangents drawn from external point are equal.

AF + BD + CE = AE + BF + CD
Perimeter of ∆ABC
= AB + BC + AC
= (AF + FB) + (BD + DC) + (AE + CE)
= AF + AE + FB + BD + DC + CE
= AF + AF + BD 4 BD + CE + CE
= 2AF + 2BD + 2CE (∵ AE - AF, FB = BD CD = CE)
= 2(AF + BD + CE)
(OR)
2(AE + BF + CD)
1/2 (Perimeter of ∆ABC)
= AF + BD + CE = AE + BF + CD
Hence, AF + BD + CE = AE + BF + CD
= 1/2 (Perimeter of ∆ABC)
Quetsion 4.
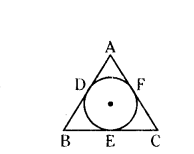
A circle is inscribed in a ∆ABC having sides 8 cm, 10 cm and 12 cm as shown in the figure. Find AD, BE and CF.
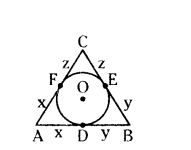
Solution:
Given a circle is inscribed in a ∆ABC.
AB = 8 cm, BC = 10 cm, AC = 12 cm
We know that tangents drawn from an external point to a circle are equal.
Let AD - AF = x cm
BD = BE = y cm and
CE = CF = z cm AB - AD + DB = 8 cm
x + y = 8 cm → (1)
BC = BE + CE = 10 cm
y + z = 10 cm → (2)
AC = AF + CF = 12 cm
x + z = 12 cm → (3)
by adding (1), (2) and (3)
(x + y) + (y + z) + (x + z) = 8 + 10 + 12
x + y + y + z + z + x = 30
2 (x + y + z) = 30
x + y + z = 30/2 = 15 cm → (4)
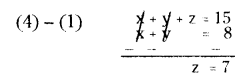
Put z = 7 in (2) y + 7 = 10
y = 10 - 7 = 3 cm
Put y = 3 cm in (1) x + 3 = 8 cm
x = 8 - 3 = 5 cm
Therefore,
AD = x = 5 cm
BE = y = 3 cm
CF = z = 7 cm
Question 5.
Prove that the angle between two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact at the centre.
Solution:
Let AP and AQ are tangents drawn to a circle from an external point to a circle with centre O.
That is AP = AQ
In ∆OAP and ∆OAQ,
AP = AQ (Tangents from the external point)
QP = QQ (Radius)
OA = OA (Common side)
by side-side-side congruency,
∆OAP ≅ ∆OAQ
by ∠PCT - ∠OAP = ∠OAQ and ∠AOP = ∠AOQ
∠OPA = ∠OQA = 90°
∠PAQ = 2, ∠OAP and ∠POQ = 2.∠AOP
In ∆AOP,
∠OAP + ∠AOP + ∠OPA = 180°
∠OAP + ∠AOP = 180° - 90° = 90°
∠AOP = 90° - ∠OAP
2.∠AOP = 2 (90 - ∠OAP)
∠POQ = 180° - 2.∠OAP (∵ 2∠AOP = ∠POQ)
∠POQ + 2.∠OAP = 180° (∵ 2∠OAP = ∠PAQ)
Hence proved, ∠POQ + ∠PAQ = 180°
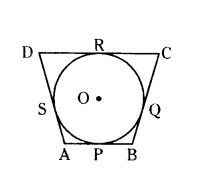
Question 6.
In the figure, a circle is inscribed in a quadrilateral ABCD in which ∠B = 90°. If AD = 23 cm, AB = 29 cm and DS = 5 cm. Find the radius of the circle.
Solution:
Given the circle touches the quadrilateral ABCD at P, Q, R and S respectively, ∠B = 90° with centre O.
AB = 29 cm. AD = 23 cm and DS = 5 cm. We know that, tangents drawn from the external point are equal.
AP = AS, BP = BQ, CQ = CR and DR = DS
AD = AS + DS = 23 cm
AS = 23 - DS = 23 - 5 = 18 cm
But, AS = AP = 18 cm
AB = AP + PB = 29 cm
18 + PB = 29
PB = 29 - 18 = 11 cm
But OPBQ is a square.
Therefore, OP = OQ = BQ = PB = 11 cm
Hence, radius r = 11 cm
Question 7.
In the given figure there are two concentric circles with centre O of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12 cm, find the length of BP.
Solution:
Given two concentric circles with centre O of radii. OA = 5 cm, OB = 3cm.
Tangent AP = 12 cm
In ∆OAP, ∠OAP = 90°
OP2 = OA2 + AP2
⇒ 52 + 122 = 169
OP = √169 = 13 cm
In ∆OBP, ∠OBP = 90°
OB2 + BP2 = OP2
32 + BP2 = 132
BP2 = 169 - 9 = 160
Therefore, BP = √169 = 4√10 cm
Quetsion 8.
Draw two tangents to a circle of radius 2.5 cm, from a point ‘P’ at a distance of 7 cm from its centre.
Solution:
- Draw u line segment PO = 7 cm.
- From the point O, draw a circle of radius = 2.5 cm.
- Draw a perpendicular bisector of PO. Let M be the mid-point of PO.
- Taking M as centre and 0M as radius, draw a circle.
- Let this circle intersects the given circle at the point Q and R.
- Join PQ and PR.
Question 9.
Two concentric circles of radii 10 cm and 6 cm are drawn. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:
Radius of outer circle = R = 10 cm
Radius of inner circle = r = 6 cru
Given that AB in a chord of outer circle and tangent to inner circle of P.
Draw OP ⊥ AB
Then PA = PB
In ∆ OAP,
∠OPA = 90°
OP2 + PA2 = OA2
62 + PA2 = 102
PA2 = 100 - 36 = 64
⇒ PA = 8 cm
∴ AB = PA + PB
= 2PA
= 2(8)
= 16 cm
Length of the chord AB = 16 cm
AP 10th Class Maths Important Questions Chapter 10 Tangents and Secants to a Circle
Question 1.
What do we call the part a and b in the below circle ?
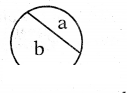
Solution:
‘a’ is minor segment and ‘b’ is major segment.
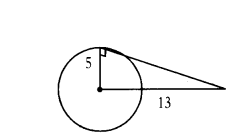
Question 2.
Find the length of the tangent to a circle of radius 7 cm at a point from a distance 25 cm from the centre.
Solution:
Given OA = 25 cm, OB = r = 7 cm
In ∆AOB, ∠B = 90°
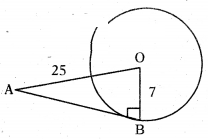
OA2 = OB2 + AB2
⇒ AB2 = OA2 - OB2 = 252 - 72
⇒AB = √252-72 = √625-49
= √576
= 24 cm
Question 3.
Find the area of a sector of a circle whose radius is 7 cm and angle at the centre is 60°.
Solution:
Radius = 7 cm, Angle at centre = 60°
Area of the sector = x/360 x πr²
= 60×22/7×7×7/360 = 154/6 = 25.66 cm2
Question 4.
A tangent is drawn to a circle of radius 4 cm. from a point that lies at a distance of 5 cm. from the centre. Find the measure of length of the tangent.
Solution:
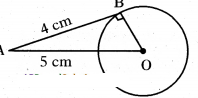
∆OAB is a right triangle.
OA2 = 0B2 + AB2
52 = OB2 + 42
OB2 = 25 -16 = 9
OB = √9 = 3 cm.
Question 5.
Find the area of the shaded part in the given figure.
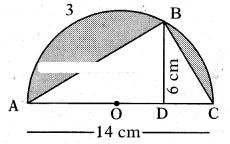
Solution:
Area of shaded part
= Area of semi-circle - Area of triangle
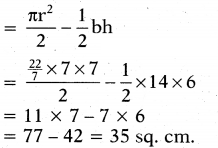
Question 1.
Find the length of the tangent from a point 13 cm away from the centre of the circle of radius 5 cm.
Solution:
Radius of the circle = 5 cm
Length of the tangent = x cm
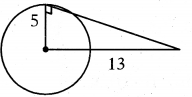
Distance between centre to point be = 13 cm
132 = 52 + x2
x2 = 169 - 25 = 144 ⇒ x = 12 cm
Question 2.
If tangents PA and PB from a point P to a circle with centre ‘O’ are inclined to each other at angle of 80°, then find the measured of ∠POA.
Solution:
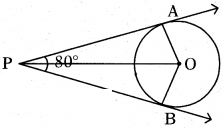
Between ∆A0P and ∆B0P
∠OAP = ∠OBP = 90° (∵ tangent and line from origin meet at 90° to each other)
0A=0B = radius of the circle = r (say)
and OP is the common side
Hence, we can say ∆AOP = ∆BOP
Therefore, we can say
∠OPA = ∠OPB = 1/2 (∠APB)
= 1/2 (80°) = 40°
(∵ given that tangents PA and PB are inclined to each other by 80°)
Now, in ∆AOP,
∠POA + ∠OPA + ∠A = 180°
⇒ ∠POA + 40° + 90° = 180°
⇒ ∠POA = 50°
Question 3.
Draw a circle of radius 3 cm, mark a point ‘P’ on the circle and draw a tan gent at ‘P’.
Solution:
Steps of construction:
1) Draw a circle of radius ‘3’ cm from the centre "O" and pick a point ‘P’ on the circle. Join OP
2) Now draw a perpendicular at the point ‘P’ to the line segment OP
such that XY ⊥ OP.
3) Then XY is the desired tangent at ‘P’ to the given circle.
Question 4.
A chord of a circle of radius 10 cm. subtends a right angle at the centre. Find the area of the corresponding minor segment (use π = 3.14),
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
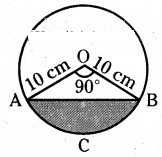
Area of sector OACB = x/360 × πr²
= 90°/360° × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of ∆ AOB = 1/2 × 10 × 10
= 50 cm2
Area of the Minor Segment = Area of sector OACB - Area of ∆ OAB
= 78.5 - 50.0 = 28.5 cm2
Question 1.
A chord of circle of radius 10 cm sub-tends a right angle at the centre. Find the area of the corresponding :
i) Minor segment ii) Major segment (use π = 3. 14)
Solution:
Radius of circle (r) = 10 cm
Sector angle (x) = 90°
Radius of sector (r) = 10 cm.
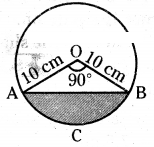
Area of sector OACB = x/360 × πr2
= 90°/360° × 3.14 × 10 × 10
= 78.5 Sq. cm
Area of ∆ AOB = 1/2 × 10 × 10
= 50 cm2
Area of the Minor Segment = Area of sector OACB - Area of ∆ OAB
= 78.5 - 50.0 = 28.5 cm2
Area of Major Segment = Area of the circle - Area of the Minor Segment
= (3.14 × 10 × 10) - 28.5
= 314-28.5 = 285.5 cm2
Question 2.
Draw a circle of radius 3 cm. Take a point ’P’ at a distance of 5 cm from the centre of the circle. From P, draw 2 tangents to the circle.
Solution:
Award marks for construction as follows:
i) To draw a circle with radius 3 cm
ii) To plot a point P such that OP = 5 cm.
iii) To Bisect QP at M and draw circle with radius OM br MP
iv) To draw tangents from intersecting points of two circles.
Question 3.
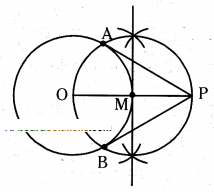
Draw a Circle of radius 4 cm. From a point 7.5 cm away from its centre, construct the pair of tangents to the circle.
Solution:
1) Draw a circle with:radius 4 cm with centre O.
2) Locate a point P such that OP 7.5 cm
3) Bisect OP and draw circle with radius MO or MP with centre M.
4) Draw tangents PA and PB from external point P to the given circle.
Question 4.
Draw a circle of radius 5 cm. From a point 8 cm away from its centre, con-struct a pair of tangents to the circle. Find the lengths of tangents.
Solution:
Steps of construction :
1) Construct a circle with a radius of 5 cm.
2) Trace the point ‘p’ in the exterior of the circle which is at a distance of ‘8’ cm from its centre.
3) Construct a perpendicular bisector to OP which meets at M.
4) The draw a circle with a radius of MP or MO from the point M. This circle cuts the previous circle drawn from the centre ‘O’ at the points A and B.
5) Now join the points PA and then PB.
6) PA, PB are the required tangents which are measured 6.2 cm long.
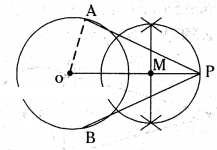
OA = 5 cm ; OP = 8 cm
AP = PB = 6.2 cm.
Question 5.
Draw a circle of radius 4 cm and draw a pair of tangents to the circle, which are intersecting each other 6 cm away from the centre.
Solution:
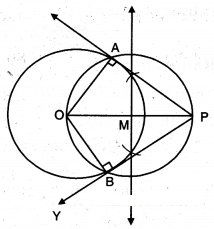
Steps of Construction:
1) Draw a circle with centre ‘O’ and radius 4 cm.
Take a point ‘P’ outside the circle such that OP = 6 cm. Join OP.
Draw the perpendicular bisector to OP which bisects it at M.
4) Taking M as centre and PM or MO as radius draw a circle.
Let the circle intersects the given circle at ’A’ and ‘B’.
Join P to A and B.
PA and PB are the required tangents of lengths.
Question 6.
Two tangents TP and TQ are drawn to a circle with centre ‘O’ from an external point T, then prove that ∠PTQ = 2. ∠OPQ.
Solution:
Given a circle with centre 0.
Two tangents TP, TQ are drawn to the circle from an external point T.
We need to prove ∠PTQ = 2∠OPQ
Let ∠PTQ = θ
TP = TQ (The lengths of tangents drawn from an external point to a circle are equal)
So ∆TPQ is an isosceles triangle
∴ ∠TPQ + ∠TQP + ∠PTQ = 180°
(Sum of three angles in a triangle)
∠TPQ = ∠TQP = 1/2 (180° - θ)
= 90°- θ/2
∠OPQ = ∠OPT - ∠TPQ
= 90° - 0(90° - θ/2) = θ/2
= 1/2 ∠PTQ
∴∠PTQ = 2∠OPQ
Question 7.
Find the area of the segment shaded in the figure in which PQ = 12 cm, PR = 5 cm and QR is the diameter of the circle with centre ‘O’. (Take π = 22/7)
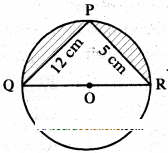
Solution:
To find the area of the segment shaded in the given figure.
Here ‘PQ’ = 12 cm; ‘PR’ = 5 cm; ‘QR’ is diameter
Now PQOR is a semicircle then angle in a semicircle is 90°.
then ∠QPR = 90°
∴ ∆PQR is a right angled triangle
∴ Area of ∆PQR = 1/2 bh
= 1/2 × PQ × PR
= 1/2 × 12 × 5 =30 cm2 .....(1)
Now the area of shaded part = area of semicircle - area of ∆PQR
= 1/2 πrcm2 - 30 cm2 ......(2)
In ∆PQR, QR2 = PQ2 + PR2
(from Pythagoras theorem)
QR2 = 122 + 52
= 144 + 25 = 169 = 132
∴ QR =13 then
Radius of the circle (r) = QO = QR/2
= 13/2 = 6.5 cm
then area of semicircle
= 1/2 πrcm2
= 1/2 × 22/7 × 13/2 × 13/2 = 66.39 cm2 ......(3)
Now putting the values of (1) and (3) in (2) we get
Area of shaded part = (66.39 - 30)
= 36.39 cm2.
Question 8.
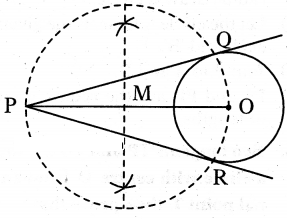
Draw two tangents to a circle of radius 2.5 cm, from a point ‘P’ at a distance of 7 cm from its centre.
Solution:
1. Draw a line segment PO = 7 cm.
2. From the point O, draw a circle of radius = 2.5 cm.
3. Draw a perpendicular bisector of PO. Let M be the mid-point of PO.
4. Taking M as centre and OM as radius, draw a circle.
5. Let this circle intersects the given circle at the point Q and R.
6. Join PQ and PR.
Question 1.
As shown in the figure, radius of the given circle is 21 cm and ∠AOB = 120°. Then find the area of segment AYB.
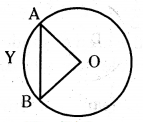
Solution:
Given radius of area = OA = OB = 21 cm
Now3 the angle at centre for the sector ˆOAB = 120°.
Formula for area of sector = x/360 x πrcm2
= 120/360 × 22/7 × 21 × 21
= 22 × 21 = 462 cm2 ......... (1)
Now area of segment ˆAYB
= Area of sector - area of ∆ OAB.
Let OD is perpendicular to AB, then
∠AOB = 120/2 = 60°
∴ sin 60° = AD/OA
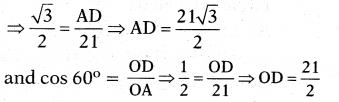
∴ area of ∆OAB = 1/2 bh
= 1/2 × AB × OD = AD × OD
= = 190.95 cm2 ...... (2)
∴ area of segment ˆAYB
= 462 - 190.95
= 271.05 cm2
= 271.05 cm2
Question 2.
In a wall clock, length of minutes needle is 7 cm. Then find the area covered by it in 10 minutes of time.
Solution:
Length of minutes needle =(r) = 7 cm
We need to calculate the area covered by in 10 minutes of time = Area of sector.
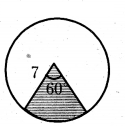
Now the angle covered by it in 60 minutes = 360°
∴ In 10 minutes = 360/60 × 10 = 60°
Area of sector = × 7 × 7
= 154/6 = 77/3
∴ Area covered by it in 10 minutes of time = 77/3 cm2 = 25.66 cm2
Question 3.
Find the area of a right hexagon inscribed in a circle having 14 cm of radius.
Solution:
Radius of circle = OA = OB = OC = OD = OE = OF = 14 cm
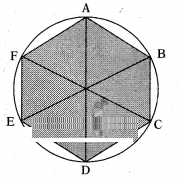
∠AOB = 360/60 = 60°
∴ In ∆AOB AO = BO = 14 cm
∠AOB = 60°
then ∠OAB = ∠OBA
(∵ Opposite to equal sides)
And ∠OAB + ∠OBA + 60 = 180
=> ∠OAB = ∠OBA = ∠AOB = 60°
Hence it is an equilateral triangle.
∴ OA = OB = AB = 14 cm
∴ Area of hexagon = 6 (Area of ∆AOB)
= 6. √3/4 a2
= 6. √3/4 × 14 × 14
Area of hexagon = 294 √3 cm2
Question 4.
Four carrorp board pans are arranged as shown in figure. Radius of the pan is 3 cm each. Then find the area in between of them.
Solution:
Area in between 4 pans = Area of square ABCD formed by joining their centres - 4 (area of sector)

Now side of square ABCD = 3 + 3 = 6
Then area of square ABCD
= 6 × 6
= 36 cm2
and now area of sector = x/360 × πr2
Area of 4 sectors
= 4 × 90/360 × 22/7 × 3 × 3
= 198/7 = 28.3 cm2
∴ Area in between 4 pans i.e., shaded
= 36 - 28.3 = 7.7 cm2