Contents
- 1 Question 1. If A = [2−10115] and B = [−10110−2] then find (AB’)’
- 2 Question 2. If A = ⎡⎣⎢−25−1104⎤⎦⎥ and B = [−243012] then find 2A + B’ and 3B’ – A.
- 3 Question 3. If A = [2−5−43] then find A + A’ and A. A’ (May 2007) (Board Model Paper)
- 4 Question 4. If A = ⎡⎣⎢−12325x367⎤⎦⎥ is a symmetric matrix then find x.
- 5 Question 5. If A = ⎡⎣⎢0−2−120x1−20⎤⎦⎥ is a skew symmetric matrix, find x. (May 2014, 11)
- 6 Question 6. Is ⎡⎣⎢0−1−410−7470⎤⎦⎥ a symmetric or skew symmetric?
- 7 II. Question 1. If A = [cosα−sinαsinαcosα], show that A . A’ = A’ . A = I2. (March 2007)
- 8 Question 2. If A = ⎡⎣⎢12354−130−5⎤⎦⎥ and B = ⎡⎣⎢201−1−22050⎤⎦⎥, then find 3A – 4B’.
- 9 Question 4. For any square matrix A; show that A A’ is symmetric. (March 2015-A.P)
Question 1.
If A = [2−10115] and B = [−10110−2] then find (AB’)’
Answer:
We have (AB)’ = B’A’
and (AB’)’ = (B’)’ A’ = BA’ (∵ (B )’ = B)

Question 2.
If A = ⎡⎣⎢−25−1104⎤⎦⎥ and B = [−243012] then find 2A + B’ and 3B’ – A.
Answer:
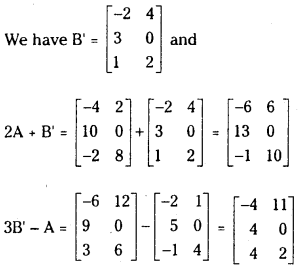
Question 3.
If A = [2−5−43] then find A + A’ and A. A’ (May 2007) (Board Model Paper)
Answer:
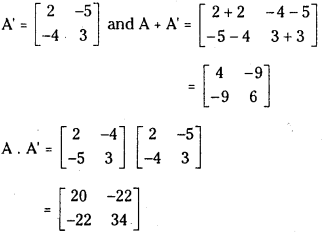
Question 4.
If A = ⎡⎣⎢−12325x367⎤⎦⎥ is a symmetric matrix then find x.
Answer:
A matrix ‘A’ is said to be symmetric if A’ = A
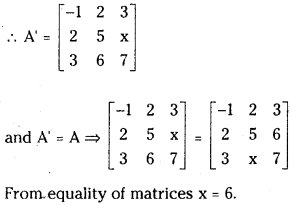
Question 5.
If A = ⎡⎣⎢0−2−120x1−20⎤⎦⎥ is a skew symmetric matrix, find x. (May 2014, 11)
Answer:
A matrix A is said to be skew symmetric if A’ = – A
from equality of matrix x = 2
Question 6.
Is ⎡⎣⎢0−1−410−7470⎤⎦⎥ a symmetric or skew symmetric?
Answer:
Let A =
i.e., A’ =
∴ The matrix A is a skew symmetric matrix.
Answer: Answer: Question 3. Answer: Answer:
Question 1.
If A =

Question 2.
If A =

If A =

Question 4.
For any square matrix A; show that A A’ is symmetric. (March 2015-A.P)
By definition a matrix is said to be symmetric if A’ = A.
∴(A A’)’ = (A’)’ A’ = A A’
[(∵ (AB)’ = B’A’ and (A’)’ = A]
Hence AA’ is a symmetric matrix.



