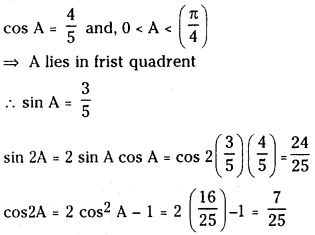TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(d)

I.
Question 1.
Simplify
(i) $\frac{\sin 2 \theta}{1+\cos 2 \theta}$

Answer:

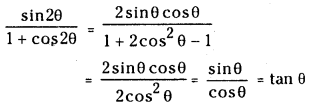
(ii) $\frac{3 \cos \theta+\cos 3 \theta}{3 \sin \theta-\sin 3 \theta}$
Answer:

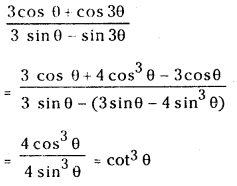
Question 2.
Evaluate the following
(i) 6sin 20° – 8 sin³ 20°

Answer:
2(3 sin 20° – 4sin³ 20°) (Formula)
= 2.sin (3 × 20°) = 2 sin 60°
= $\frac{2 \sqrt{3}}{-2}$ = √3

(ii) cos²72° – sin²54°
Answer:
cos²72° – sin²54°
= sin²18° – cos²36°

(iii) sin²42° – sin²12°
Answer:
sin²42° – sin²12° (Formula)
sin (42° + 12°) sin (42° – 12°)
= sin 54° sin 30°
= $\left(\frac{\sqrt{5}+1}{4}\right) \frac{1}{2}=\frac{\sqrt{5}+1}{8}$

Question 3.
(i) Express $\frac{\sin 4 \theta}{\sin \theta}$ in terms of cos3 θ and cos θ.

Answer:
sin4θ = sin (3θ + θ) = sin 3θ cos θ +cos 3θ sin θ
= (3 sin θ – i sin 3θ) cos θ + (4 cos 3θ – 3 cos θ) sin θ
= 3 sin θ cos θ – 4 sin 3θ cos θ + 4 cos 3θ sin θ – 3 cos θ sin θ
= 4 cos 3θ sin θ – 4 sin 3θ cos θ
= sin θ(1 cos 3θ – 4 sin 2θ cos θ)
= sin θ [4 cos 3θ – 4 sin 2θ cos θ]
∴ $\frac{\sin 4 \theta}{\sin \theta}=\frac{\sin \theta\left(4 \cos ^3 \theta-4 \sin ^2 \theta \cos \theta\right)}{\sin \theta}$
= 4 cos 3θ – 4 sin 2θ cos θ
= 4 cos 3θ – 4 (1- cos 2θ) cos θ
= 8 cos 3θ – 4 cos θ

(ii) Express cos⁶ A + sin⁶ A in terms of sin 2A.
Answer:
cos⁶A + sin⁶A = (cos²A + sin²A)³
= (cos²A + sin²A)³ – 3 cos²A sin²A (cos²A + sin² A)
= 1 – 3 cos²A sin²A ……………(1)
= 1 – $\frac{3}{4}$ (4 cos² A sin² A)
= 1 – $\frac{3}{4}$sin²2A

(iii) Express $\frac{1-\cos \theta+\sin \theta}{1+\cos \theta+\sin \theta}$ in terms of tan $\frac{\theta}{2}$
Answer:

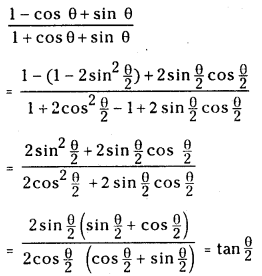
Question 4.
(i) If sin α = $\frac{3}{5}$, where $\frac{\pi}{2}$ < α < π, evaluate cos 3α and tan 2α. (March 2015-T.S)

Answer:
since $\frac{\pi}{2}$ < α < π, a lies in second quadrant and given sin α = $\frac{3}{5}$ we have cos α = –$\frac{4}{5}$
cos 3α = 4 cos³ α – 3 cos α

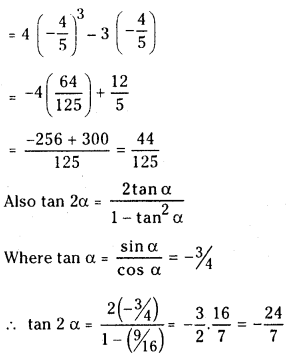
(ii) If cos A = $\frac{7}{25}$ and $\frac{3 \pi}{2}$ < A < 2π, then find the value of cot $\frac{A}{2}$.
Answer:

(iii) If 0 < θ < $\frac{\pi}{8}$, show that $\sqrt{2+\sqrt{2+\sqrt{2+2 \cos 4 \theta}}}$ = 2cos(θ/2)
Answer:

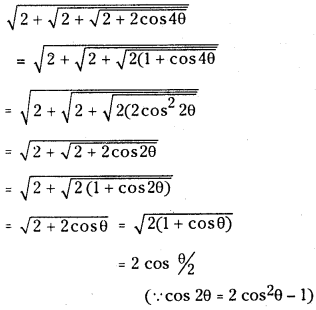
Question 5.
Find the extreme values of
(i) cos 2x + cos2x

Answer:
cos 2x + cos2x = 2 cos² x – 1 + cos² x
= 3 cos² x – 1
and 0 ≤ cos² x ≤ 1
⇒ 0 ≤ 3 cos² x ≤ 3
⇒ -1 ≤ 3 cos² x – 1 ≤ 2
Maximum value = 2
and minimum value = -1
(or) cos 2x + cos² x = cos 2x + $\left(\frac{1+\cos 2 x}{2}\right)$
We have -1 < cos 2x ≤ 1
⇒ -3 ≤ 3 cos 2x ≤ 3
⇒ -2 ≤ 3 cos 2x + 1 ≤ 4
⇒ -1 ≤ $\frac{3 \cos 2 x+1}{2}$ ≤ 2
Maximum value = 2
Minimum value = -1

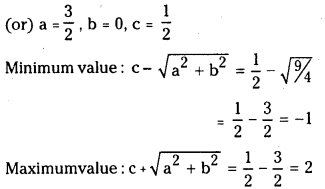
(ii) 3sin²x + 5 cos²x
Answer:
3sin²x + 5 cos²x

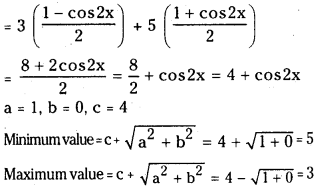
Question 7.
Find the periods for the following functions
(i) cos⁴x

Answer:

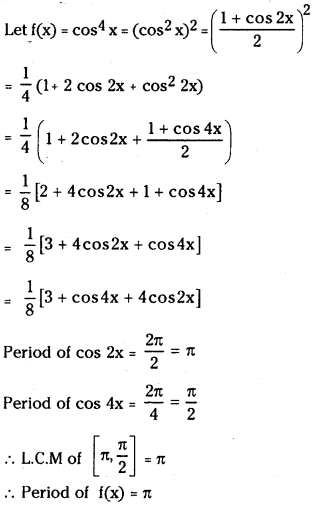
(ii) 2sin$\left(\frac{\pi \mathbf{x}}{\mathrm{4}}\right)$ + 3cos$\left(\frac{\pi x}{3}\right)$
Answer:

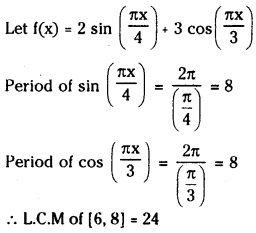
(iii) sin²x + 2 cos²x
Answer:
Let f(x) = sin²x + 2cos²x

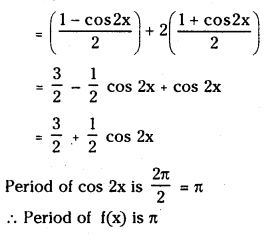
(iv) 2sin($\frac{\pi}{4}$ + x)cos x
Answer:

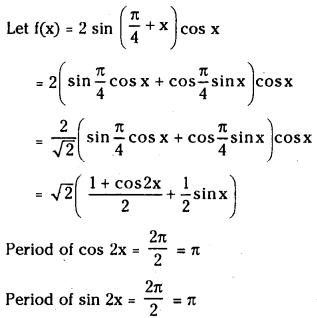
Period of f(x) is LCM of [π, π] = π

(v) $\frac{5 \sin x+3 \cos x}{4 \sin 2 x+5 \cos x}$
Answer:

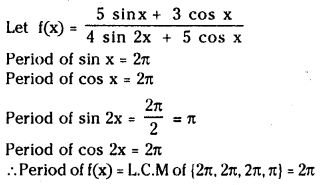
II.
Question 1.
(i) If 0 < A < $\left(\frac{\pi}{4}\right)$, and cos A = $\frac{4}{5}$, find the values of sin 2A and cos 2A.

Answer: