Contents
- 1 I. Question 1. Simplify the following (i) cos 100° . cos 40° + sin 100° . sin 40°
- 2 Question 4. (i) Prove that cos 35° + cos 85° + cos 155° = 0
- 3 Question 5. Evaluate (i) sin28212∘ – sin22212∘
- 4 Question 6. Find the minimum and maximum values of (i) 3 cos x + 4 sin x
- 5 Question 7. Find the range of (i) 7 cos x – 24 sin x + 5
- 6 II. Question 1. (i)If cos α = –35 and sin β = 725 where π2 < α < π and 0 < β < π2, then find the values of tan(α + β) and sin(α + β).
- 7 Question 2. i) Find the expansion of sin (A + B – C).
I.
Question 1.
Simplify the following
(i) cos 100° . cos 40° + sin 100° . sin 40°
Answer:
Use cos A. cos B + sin A sin B = cos (A – B)
∴ cos 100° . cos 40° + sin 100°.sin 40°
= cos (100° – 40°)
= cos 60°
=
(ii)
Answer:
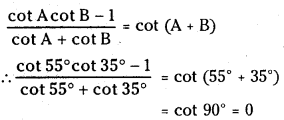
(iii) tan [
Answer:

(iv) Evaluate Σ
Answer:
Σ
= Σ (cot A – cot C)
= cot A – cot C + cot B – cot A + cot C – cot B = 0
Question 4.
(i) Prove that
cos 35° + cos 85° + cos 155° = 0
Answer:
cos 35° + cos 85° + cos 155°
= cos 35° + 2cos
= cos 35° + 2 cos 120° cos (-35°)
= cos 35° – cos 35° = 0
(ii) tan 72° = tan 18° + 2 tan 54°
Answer:
We have cot A – tan A =
⇒
∴ cot A – tan A = 2 cot 2A
⇒ cot A = tan A + 2 cot 2A°
Take A = 18°, then cot 18° = tan 18° + 2 cot 36°
⇒ cot(90 – 72) = tan 18° + 2 cot(90 – 54)
⇒ tan 72° = tan 18° + 2 tan 54°
(iii) sin 750° cos 480° + cos 120° cos 60° = –
Answer:
L.H.S = sin [2.(360) + 30] cos[360 + 120] + cos 120 cos 60
= sin 30 cos 120 + cos 120 cos 60
=
(iv) cos A + cos(
Answer:
Use cos(A + B) + cos(A – B) = 2cos A cos B
L.H.S = cos A + 2cos
= cos A + 2 cos 240 cos A
= cos A + 2 cos ( 180 + 60) cos A
= cos A + 2 ( – cos 60) cos A
= cos A + 2
(v) cos2θ + cos2(
Answer:
cos2θ + cos2( 120 + θ) + cos2( 120 – θ)
= cos2θ + cos2(120 + θ) + 1 – sin2(120 – θ)
= 1 + cos2θ + cos [ 120 + θ + 120 – θ] cos [ 120 + θ- 120 + θ]
= 1 + cos2θ + cos (240) cos 2θ
= 1 + cos2θ + cos (180 + 60) cos 2θ
[∵ Use cos2A – sin2B = cos (A + B) cos (A – B)]
= 1 + cos2θ – cos 60 ( 2 cos2θ – 1)
= 1 + cos2θ –
= 1 + cos2θ – cos2 θ +
Question 5.
Evaluate
(i) sin28212∘ – sin22212∘
Answer:
sin282
= sin[82
∵ Use sin2A – sin2B = sin(A + B) sin(A – B)
= sin 105° . sin 60°
= sin 60° sin (60° + 45°)
= sin 60° [sin 60° cos 45° + cos 60° sin 45°]
=
(ii) cos2 112
Answer:
Use cos2 A – sin2 B = cos (A + B) cos (A – B)
cos2112
= cos [112
= cos 165° . cos 60
= cos 60° cos (180 – 15)
= -cos 60°. cos 15°
=
(iii) sin2
Answer:
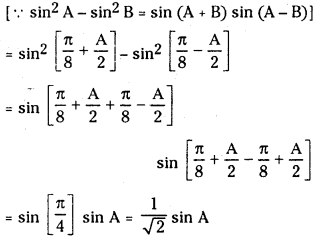
(iv) cos252
Answer:
[∵ cos2A – sin2B = cos (A + B) cos (A – B)]
cos252
= cos[52
= cos 75° cos 30°
= cos 30° cos(90 – 15)
= cos 30° sin 15°
=
Question 6.
Find the minimum and maximum values of
(i) 3 cos x + 4 sin x
Answer:
Recall for a cos x + b sin x + c
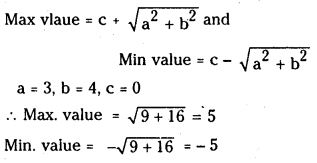
(ii) sin 2x – cos 2x
Answer:
a = 1, b = -1, c = 0
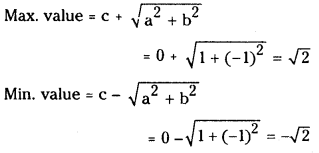
Question 7.
Find the range of
(i) 7 cos x – 24 sin x + 5
Answer:
a = -24, b = 7, c = 5
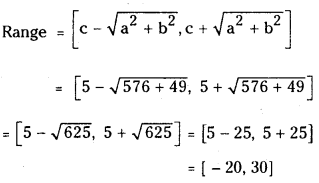
(ii) 13 cos x + 3√3 sin x – 4
Answer:
a = 3√3, b = 13, c = -4
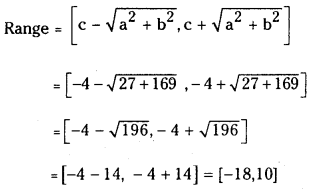
II.
Question 1.
(i)If cos α = –35 and sin β = 725 where π2 < α < π and 0 < β < π2 , then find the values of tan(α + β) and sin(α + β).
Answer:
cos α = –
sin α =
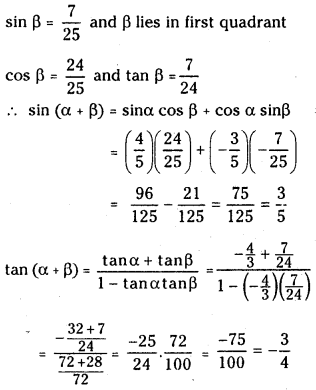
(ii) If 0 < A < B <
Answer:

(iii) If A + B, A are acute angles such that sin (A + B) =
Answer:
A + B, A are acute angles ⇒ B is also acute.
Given sin (A + B) =
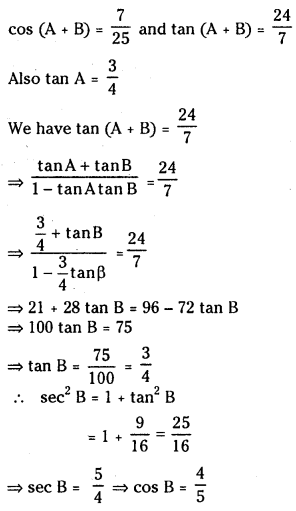
(iv) If tan α – tan β = m, and cot α – cot β = n then prove that cot(α – β) =
Answer:
We have tan α – tan β = m
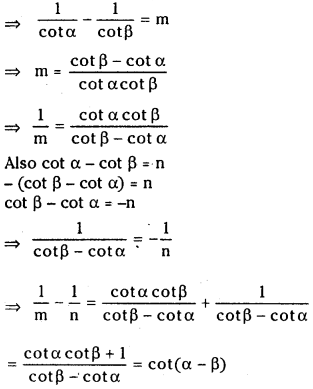
(v) If tan (α – β) =
Answer:

Question 2.
i) Find the expansion of sin (A + B – C).
Answer:
0 sin (A + B – C) = Sin [ (A + B) – C]
= sin (A + B) cos C – cos (A + B) sin C] – (sin A cos B + cos A sin B) cos C – (cos A cos B – sin A sin B] sin C
= sin A cos B cos C + cos A sin B cos C – cos A cos B sin C – sin A sin B sin C
ii) Find the expansion of cos (A – B – C).
Answer:
cos (A – B – C) = cos [(A – B) – C]
= cos (A – B) cos C + sin (A – B) sin C
= (cos A cos B + sin A sin B) cos C + (sin A cos B – cos A sin B] sin C
= cos A cos B cos C + sin A sin B cos C + sin A cos B sin C – cos A sin B sin C
iii) In a ΔABC, A is obtuse. If sin A =
Answer:
Given, A + B + C = 180°
⇒ A + B = 180° – C
∴ sin (A + B) = sin (180° – C)
= sin C ………………..(1)
∴ A is obtuse angle and A lies in II quadrant.
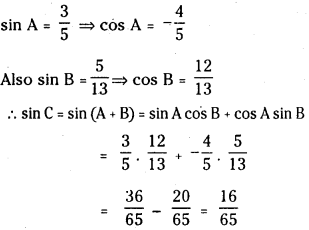
iv) If
Answer:



