Contents
- 1 TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(b)
- 1.1 I. Question 1. Find the following products wherever possible. i) [-1 4 2]⎡⎣⎢513⎤⎦⎥
- 1.2 Question 2. If A = [1−4−2235] and B = ⎡⎣⎢242351⎤⎦⎥ do AB and BA exist ? If they exist find them. Do A and B commute with respect to multiplication.
- 1.3 Question 3. Find A2 where A = [4−121]
- 1.4 Question 4. If A = [i00i] find A2.
- 1.5 Question 5. If A = [i00−i]; B = [01−10] and C = [0ii0] and I is the unit matrix of order 2, then show that i) A2 = B2 = C2 = – I
- 1.6 Question 6. If A = [2113] and B = [312004] find AB. Find BA if it exists. Answer: Given A = [2113] and B = [312004] are matrices of 2 × 2 and 2 × 3. The resulting matrix AB is of the form 2 × 3. Question 7. If A = [2−14K] and A2 = 0 then find the value of K. (May 2011, Mar. ’14, ’05)
- 1.7 II. Question 1. If A = ⎡⎣⎢300030003⎤⎦⎥ there find A4.
- 1.8 Question 2. If A = ⎡⎣⎢15−212−136−3⎤⎦⎥ then Find A3.
- 1.9 Question 3. If A = ⎡⎣⎢103−21−11−11⎤⎦⎥ then find A3 – 3A2 – A – 3I, where I is a unit matrix of order 3. (March 2011)
- 1.10 Question 4. If I = [1001] and E = [0010] show that (aI + bE) = a3I + 3a2bE, where I is a unit matrix of order 2. (Mar. 2015-A.P)(May ’05)|
- 1.11 III. Question 1. If A = diag[a1 a2 a3] then for any Integer n ≥ 1 show that An = diag[an1,an2,an3]
- 1.12 Question 2. If θ – Φ = π2, then show that [cos2θcosθsinθcosθsinθsin2θ][cos2ϕcosϕsinϕcosϕsinϕsin2ϕ] = 0
- 1.13 Question 3. If A = [31−4−1], then show that An = [1+2nn−4n1−2n] for any integer n ≥ 1, by using mathematical induction.
- 1.14 Question 4. Given examples of two square matrices A and B of the same order for which AB = 0 but BA ≠ 0.
- 1.15 Question 5. A trust fund has to invest Rs. 30,000 in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication determine how to divide Rs. 30,000 among the two types of bonds, if the trust fund must obtain an annual total interest of (a) Rs. 1800 and (b) Rs. 2,000.
TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(b)
I.
Question 1.
Find the following products wherever possible.
i) [-1 4 2]⎡⎣⎢513⎤⎦⎥
Answer:
It is a product of 1 × 3 and 3 × 1 matrices and the resulting is an 1 × 1 matrix.
[-1 4 2]
= [-1 × 5 + 4 × 1 + 2 × 3]1 × 1 = [5]1 × 1
ii)
Answer:
It is a product of 2 × 3 and 3 × 1 matrices and the resulting is an 2 × 1 matrix.
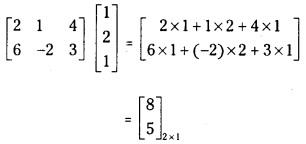
iii)
Answer:
Product of 2 × 2 and 2 × 2 matrices and the resulting is an 2 × 2 matrix.
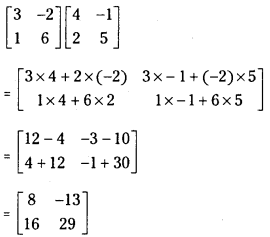
iv)
Answer:
Product of 3 × 3 and 3 × 3 matrices and the resulting is an 3 × 3 matrix.

v)
Answer:
Product of A3 × 3 and B2 × 3 matrices. Matrix multiplication is not confirmable since the number of columns of A ≠ number of rows of B.
vi)
Answer:
Product of A3 × 1 and B2 × 3 matrices. Matrix multiplication is not confirmable since the number of coloumn of A ≠ number of rows of B.
vii)
Answer:
Product of 2 × 2 and 2 × 2 matrices and the resulting is an 2 × 2 matrix.
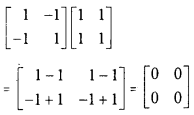
viii)
Answer:
Product of 3 × 3 and 3 × 3 matrices and the resulting matrix is an 3 × 3 matrix.

Question 2.
If A = [1−4−2235] and B = ⎡⎣⎢242351⎤⎦⎥ do AB and BA exist ? If they exist find them. Do A and B commute with respect to
multiplication.
Answer:
Given A =
We have the product of A2×3 and B3×2 matrices and resulting AB is a product matrix of order 2 × 2. Similarly the product of B3×2 and A2×3 matrices results a product matrix BA of order 3 × 3.

Since AB ≠ BA, we have A and B are not com¬mutative with respect to multiplication of matrices.
Question 3.
Find A2 where A = [4−121]
Answer:
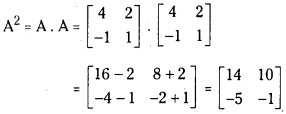
Question 4.
If A = [i00i] find A2.
Answer:
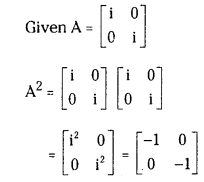
Question 5.
If A = [i00−i] ; B = [01−10] and C = [0ii0] and I is the unit matrix of order 2, then show that
i) A2 = B2 = C2 = – I
Answer:
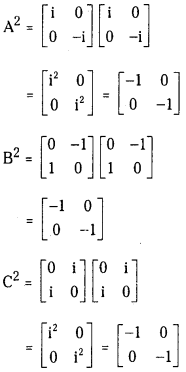
ii) AB = – BA = – C (March 2008)
Answer:
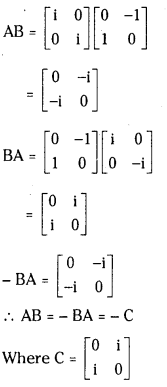
Question 6.
If A = [2113] and B = [312004] find AB. Find BA if it exists.
Answer:
Given A = [2113] and B = [312004] are matrices of 2 × 2 and 2 × 3. The resulting matrix AB is of the form 2 × 3.
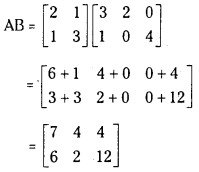
Question 7.
If A = [2−14K] and A2 = 0 then find the value of K. (May 2011, Mar. ’14, ’05)
Answer:
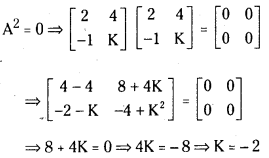
II.
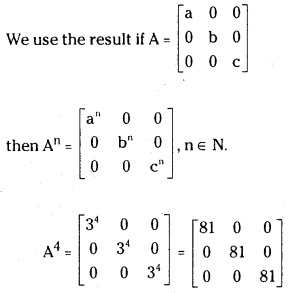
Question 1.
If A = ⎡⎣⎢300030003⎤⎦⎥ there find A4.
Answer:
Question 2.
If A = ⎡⎣⎢15−212−136−3⎤⎦⎥ then Find A3.
Answer:

Question 3.
If A = ⎡⎣⎢103−21−11−11⎤⎦⎥ then find A3 – 3A2 – A – 3I, where I is a unit matrix of order 3. (March 2011)
Answer:

Question 4.
If I = [1001] and E = [0010] show that (aI + bE) = a3I + 3a2bE, where I is a unit matrix of order 2. (Mar. 2015-A.P)(May ’05)|
Answer:
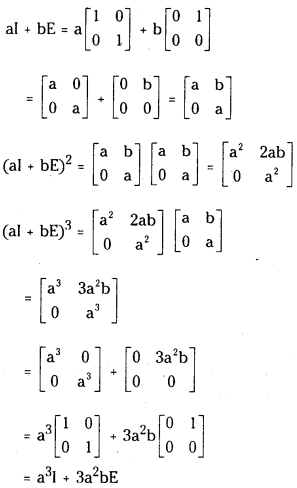
III.
Question 1.
If A = diag[a1 a2 a3] then for any Integer n ≥ 1 show that An = diag[an1,an2,an3]
Answer:
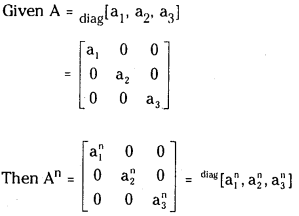
We prove this result by using mathematical induction suppose n = 1 then
A’ = ⎡⎣⎢a1000a2000a3⎤⎦⎥ = A
The result is true for n = 1.
Suppose the result for n = k then
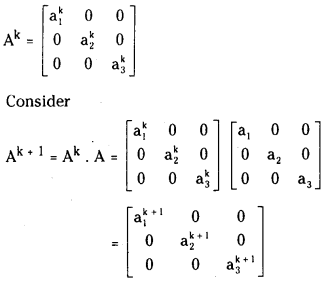
The result is true for n = k + 1.
So by the principle of mathematical induc-tion the statement is true ∀ n ∈ N.
Question 2.
If θ – Φ = π2 , then show that [cos2θcosθsinθcosθsinθsin2θ][cos2ϕcosϕsinϕcosϕsinϕsin2ϕ] = 0
Answer:
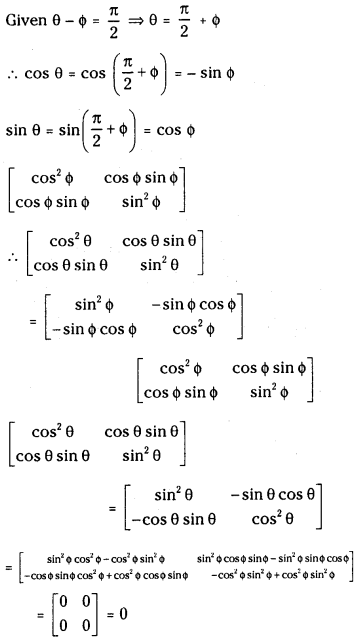
Question 3.
If A = [31−4−1] , then show that An = [1+2nn−4n1−2n] for any integer n ≥ 1, by using mathematical induction.
Answer:
We shall prove the result by mathematical induction.

∴ The given result is true for n = k + 1
∴ By Mathematical induction the given result is true for all positive integral values of n.
Question 4.
Given examples of two square matrices A and B of the same order for which AB = 0 but BA ≠ 0.
Answer:
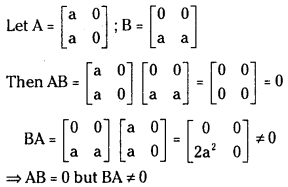
Question 5.
A trust fund has to invest Rs. 30,000 in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication determine how to divide Rs. 30,000 among the two types of bonds, if the trust fund must obtain an annual total interest of (a) Rs. 1800 and (b) Rs. 2,000.
Answer:
Let the first bond be ‘x’, then the second bond will be 30,000 – x.
Rate of interest are 5% and 7% means 0.05 and 0.07.
a) [x 30,000 – x][0.050.07] = [1800]
⇒ 0.05x + 0.07 (30,000 – x) = 1800
⇒ – 0.02x + 0.07 (30,000) = 1800
⇒ – 0.02x + 2100 = 1800
⇒ – 0.02x = – 300
⇒ x = 3000.02 = 300 × 1002 = 15, 000
First bond = 15, 000
Second bond = 30,000 – x
= 30,000 – 15,000 = 15,000
(b) [x 30,000 – x][0.050.07] = [2000]
⇒ 0.05x + 0.07 (30,000 – x) = 2000
⇒ – 0.02x + 0.07 (30,000) = 2000
⇒ – 0.02x + 2100 = 2000
⇒ x = 1000.02 = 5, 000
∴ Second bond = 30,000 – x
= 30,000 – 5,000
= 25,000
If A =
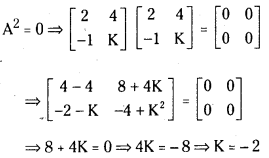
Question 1.
If A =

If A =

If A =

If I =
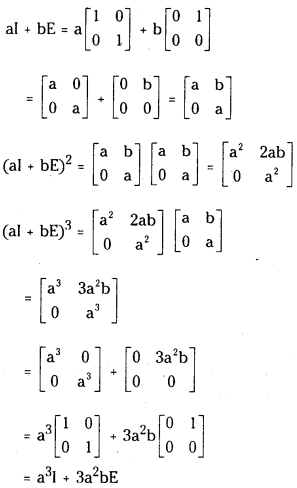
Question 1.
If A = diag[a1 a2 a3] then for any Integer n ≥ 1 show that An = diag
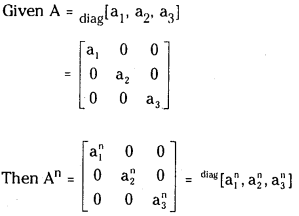
We prove this result by using mathematical induction suppose n = 1 then
A’ =
The result is true for n = 1.
Suppose the result for n = k then

The result is true for n = k + 1.
So by the principle of mathematical induc-tion the statement is true ∀ n ∈ N.
If θ – Φ =

If A =
We shall prove the result by mathematical induction.

Given examples of two square matrices A and B of the same order for which AB = 0 but BA ≠ 0.

A trust fund has to invest Rs. 30,000 in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication determine how to divide Rs. 30,000 among the two types of bonds, if the trust fund must obtain an annual total interest of (a) Rs. 1800 and (b) Rs. 2,000.
Let the first bond be ‘x’, then the second bond will be 30,000 – x.
Rate of interest are 5% and 7% means 0.05 and 0.07.
a) [x 30,000 – x]
⇒ 0.05x + 0.07 (30,000 – x) = 1800
⇒ – 0.02x + 0.07 (30,000) = 1800
⇒ – 0.02x + 2100 = 1800
⇒ – 0.02x = – 300
⇒ x =
First bond = 15, 000
Second bond = 30,000 – x
= 30,000 – 15,000 = 15,000
⇒ 0.05x + 0.07 (30,000 – x) = 2000
⇒ – 0.02x + 0.07 (30,000) = 2000
⇒ – 0.02x + 2100 = 2000
⇒ x =
∴ Second bond = 30,000 – x
= 30,000 – 5,000
= 25,000



