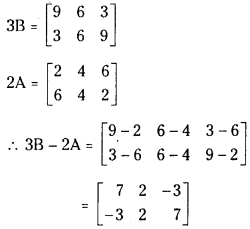Contents
- 1 TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(a)
- 1.1 Question 1. Write the following as a single matrix. (i) [2 1 3] + [0 0 0] Answer: [2 1 3] + [0 0 0] = [2 + 0 1 + 0 3 + 0] = [2 1 3] (ii) ⎡⎣⎢01−1⎤⎦⎥+⎡⎣⎢−110⎤⎦⎥ Answer: ⎡⎣⎢01−1⎤⎦⎥+⎡⎣⎢−110⎤⎦⎥ = ⎡⎣⎢0−11+1−1+0⎤⎦⎥ = ⎡⎣⎢−12−1⎤⎦⎥(iii) [31980−2]+[470124]
- 1.2 Question 2. If A = [−1432], B = [231−5], X = [x1x3x2x4] and A + B = X then find the values of x1, x2, x3 and x4.
- 1.3 Question 3. If A = ⎡⎣⎢−112−22−1343⎤⎦⎥ B = ⎡⎣⎢101−2−2252−3⎤⎦⎥ and C = ⎡⎣⎢−212110221⎤⎦⎥ then find A + B + C.
- 1.4 Question 4. If A = ⎡⎣⎢3212−23−101⎤⎦⎥, B = ⎡⎣⎢−324−11−1032⎤⎦⎥ and X = A + B then find X.
- 1.5 Question 5. If [x−3z+22y−86] = [5−22a−4] then find the values of x, y, z and a. [May 2006, Mar. 14]
- 1.6 II. Question 1. If ⎡⎣⎢x−1012z−105−y7a−5⎤⎦⎥ = ⎡⎣⎢101240370⎤⎦⎥ then find the values x, y, z and a. Answer: Given ⎡⎣⎢x−1012z−105−y7a−5⎤⎦⎥ = ⎡⎣⎢101240370⎤⎦⎥ we have x – 1 = 1, 5 – y = 3, z – 1 = 4, a – 5 = 0 ⇒ x = 2, y = 2, z = 5, a = 5 Question 2. Find the trace of ⎡⎣⎢1213−10−551⎤⎦⎥
- 1.7 Question 3. If A = ⎡⎣⎢02413524−6⎤⎦⎥ and B = ⎡⎣⎢−10021030−1⎤⎦⎥ find A – B and 4A – 5B.
- 1.8 Question 4. If A = [132231] and B = [312213] find 3B – 2A.
TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(a)
Question 1.
Write the following as a single matrix.
(i) [2 1 3] + [0 0 0]
Answer:
[2 1 3] + [0 0 0] = [2 + 0 1 + 0 3 + 0]
= [2 1 3]
📚 Top Question Papers & Study Materials
Get latest updates, guess papers and exam alerts instantly.
3,50,000+ Students Already Joined
(ii) ⎡⎣⎢01−1⎤⎦⎥+⎡⎣⎢−110⎤⎦⎥
Answer:
⎡⎣⎢01−1⎤⎦⎥+⎡⎣⎢−110⎤⎦⎥ = ⎡⎣⎢0−11+1−1+0⎤⎦⎥ = ⎡⎣⎢−12−1⎤⎦⎥
(iii) [31980−2]+[470124]
📚 Top Question Papers & Study Materials
Get latest updates, guess papers and exam alerts instantly.
3,50,000+ Students Already Joined
Answer:
Answer:
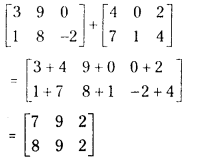
(iv)
Answer:
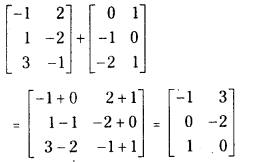
Question 2.
If A = [−1432] , B = [231−5] , X = [x1x3x2x4] and A + B = X then find the values of x1, x2, x3 and x4.
Answer:
A + B = X
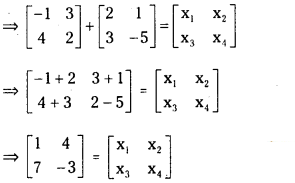
⇒ x1 = 1, x2 = 4, x3 = 7, x4 = – 3.
Question 3.
If A = ⎡⎣⎢−112−22−1343⎤⎦⎥ B = ⎡⎣⎢101−2−2252−3⎤⎦⎥ and C = ⎡⎣⎢−212110221⎤⎦⎥ then find A + B + C.
Answer:
A + B + C =
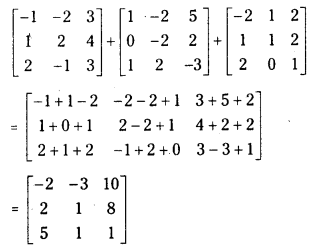
Question 4.
If A = ⎡⎣⎢3212−23−101⎤⎦⎥ , B = ⎡⎣⎢−324−11−1032⎤⎦⎥ and X = A + B then find X.
Answer:
X = A + B
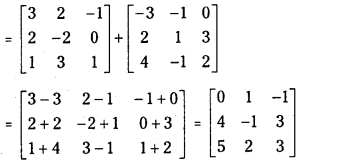
Question 5.
If [x−3z+22y−86] = [5−22a−4] then find the values of x, y, z and a. [May 2006, Mar. 14]
Answer:
Given
We have x – 3 = 5, 2y – 8 = 2, z + 2 = – 2, a – 4 = 6
⇒ x = 8, y = 5, z = – 4, a = 10
II.
Question 1.
If ⎡⎣⎢x−1012z−105−y7a−5⎤⎦⎥ = ⎡⎣⎢101240370⎤⎦⎥ then find the values x, y, z and a.
Answer:
Given ⎡⎣⎢x−1012z−105−y7a−5⎤⎦⎥ = ⎡⎣⎢101240370⎤⎦⎥
we have x – 1 = 1, 5 – y = 3, z – 1 = 4,
a – 5 = 0
⇒ x = 2, y = 2, z = 5, a = 5
Question 2.
Find the trace of ⎡⎣⎢1213−10−551⎤⎦⎥
Answer:
Trace of the given matrix
= 1 – 1 + 1 = sum of the diagonal elements
= 1
Question 3.
If A = ⎡⎣⎢02413524−6⎤⎦⎥ and B = ⎡⎣⎢−10021030−1⎤⎦⎥ find A – B and 4A – 5B.
Answer:

Question 4.
If A = [132231] and B = [312213] find 3B – 2A.
Answer:

Find the trace of
Trace of the given matrix
= 1 – 1 + 1 = sum of the diagonal elements
= 1
If A =

If A =