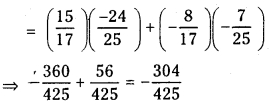TS Inter 1st Year Maths 1A Trigonometric Ratios upto Transformations Solutions Exercise 6(a)

I.
Question 1.
Convert the following into simplest form
(i) tan (θ – 14π)

Answer:
tan (θ – 14π) = tan [- (14π – θ)]
= – tan (14π – θ)
= – tan [ 2(7π) – θ)
= – tan (-θ) = tan θ

(ii) cot ($\frac{21 \pi}{2}$ – θ)
Answer:
cot ($\frac{21 \pi}{2}$ – θ) = cot[10π + ($\frac{\pi}{2}$ – θ)]
= cot ($\frac{\pi}{2}$ – θ) = tan θ

(iii) cosec (5π + θ)
Answer:
cosec (5π + θ) = cosec [4π + (π + θ)]
= cosec(π + θ) = – cosec θ

(iv) sec (4π – θ)
Answer:
sec (4π – θ) = sec [2(2π) – θ]
= sec (- θ) = sec θ

Question 2.
Find the values of each of the following
(i) sin (-405°)

Answer:
sin (-405°) = -sin 405° = -sin (360°+45°)
= – sin 45° = $-\frac{1}{\sqrt{2}}$

(ii) cos $\left(-\frac{7 \pi}{2}\right)$
Answer:
cos $\left(-\frac{7 \pi}{2}\right)$ = cos $\frac{7 \pi}{2}$ = cos (630°)
= cos (360 + 270°) = cos 270°
= cos (180 + 90) = -cos 90 = 0
(or) cos $\left(-\frac{7 \pi}{2}\right)$ = 0 (∵ cos(2n + 1)$\frac{\pi}{2}$ = 0)

(iii) sec (2100°)
Sol. sec (2100°) = sec [5 × 360° + 300°]
= sec 300° = sec (360° – 60°)
= sec 60° = 2

(iv) cot (-315°)
Answer:
cot (-315°) = – cot 315° = – cot (270 + 45°)
= cot 45° = 1

Question 3.
Evaluate
(i) cos² 45° + cos² 135° + cos² 225° + cos² 315°

Answer:
cos 45° = $\frac{1}{\sqrt{2}}$, cos 135° = cos (180 – 45°)
= – cos 45° = $-\frac{1}{\sqrt{2}}$

cos 225° = cos (180 + 45°)
= – cos 45° = –$\frac{1}{\sqrt{2}}$

cos 315° = cos(360 – 45°)
= cos 45° = $\frac{1}{\sqrt{2}}$

∴ cos² 45° + cos² 135° + cos² 225° + cos² 315°
= $\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}$ = 2

(ii) sin²$\frac{2 \pi}{3}$ + cos²$\frac{5 \pi}{6}$ – tan²$\frac{3 \pi}{4}$

Answer:

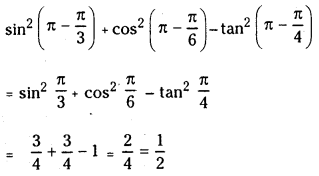
(iii) cos 225° – sin 225° + tan 495° – cot 495°
Answer:
cot (180 + 45) – sIn (180 + 45) + tan (360 + 135) – cot (360 + 135)
= – cot 45° + sin 45° + tan 135 – cot 135°
= – cos 45° + sin 45° +tan(180 – 45) – cot(180 – 45)
= – cos 45° + sin 45° – tan 45° + cot 45°
= $-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}$ – 1 + 1 = 0

(iv) (cos θ – sin θ) if
(a) θ = $\frac{7 \pi}{4}$
(b) θ = $\frac{11 \pi}{4}$
Answer:

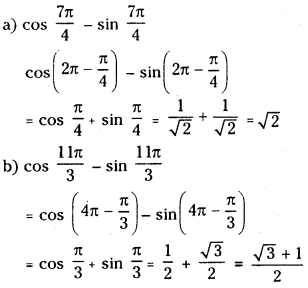
Question 4.
(i) If sin θ = –$\frac{1}{3}$ and 0 does not lie in the third 3 quadrant, find the values of (a) cos θ and (b) cot θ. (March 2013)

Answer:
sin θ = –$\frac{1}{3}$ and sin θ is negative and does not lie in third quadrant,
⇒ θ lies in fourth quadrant. In IVth quadrant cos θ is positive and cot θ is negative.
a) cos θ = $\sqrt{1-\sin ^2 \theta}=\sqrt{1-\frac{1}{9}}=\frac{2 \sqrt{2}}{3}$
b) cot θ = $\frac{\cos \theta}{\sin \theta}$ = -2√2

(ii) If cos θ = t (0 < t < 1) and θ does not lie in the first quadrant, find the values of a) sin θ b) tan θ
Answer:
cos θ = t, (0 < t < 1)
⇒ cos θ is positive and 0 does not lie in first quadrant
⇒ θ lies in IVth quadrant
a) sin θ = $-\sqrt{1-\cos ^2 \theta}=-\sqrt{1-t^2}$
b) tan θ = $\frac{\sin \theta}{\cos \theta}=-\frac{\sqrt{1-t^2}}{t}$

(iii) Find the value of sin 330°. cos 120° + cos 210°. sin 300°
Answer:
sin 330° cos 120° + cos 210° sin 300°
= sin (360 – 30) cos (180 – 60) + cos ( 180 + 30) sin (360 – 60)
= (-sin 30°) (-cos 60°) + (-cos 30°) (- sin 60°)
= sin 30 cos 60 + cos 30 sin 60 = sin (30 + 60)
= sin 90° = 1

(iv) If cosec θ + cot θ = $\frac{1}{3}$, find cos θ and determine the quadrant in which θ lies.
Answer:
we have coses²θ – cot² θ = 1
⇒ (cosec θ + cot θ) (cosec θ – cot θ) = 1

∴ sin θ is positive and cos θ is negative,
⇒ θ lies in IInd quadrant.

Question 5.
(i) If sin α + cosec α= 2, find the value of sinⁿ α + cosecⁿ α; n ∈ Z.

Answer:
Given sin α + cosec α = 2
Squaring both sides
sin² α = cosec² α + 2 = 4
⇒ sin α + cosec α = 2
cubing on both sides
sin³ α + cosec³ α + 3 sin α cosec α (sin α + cosec α) = 8
sin³ α + cosec³ α + 3 (2) = 8
⇒ sin³ α + cosec³ α = 2
In the same way sinⁿ α + cosecⁿ α = 2 (n ∈ z)

(ii) If sec θ + tan θ = 5, find the quadrant in which θ lies and find the value of sin θ
Answer:
We have sec² θ – tan² θ = 1
⇒ (sec θ + tan θ) (sec θ – tan θ) = 1
Also given sec θ + tan θ = 5 ………….(2)

Adding (1) and (2)

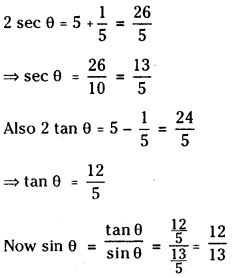
tan θ is +ve, sec θ is + ve
⇒ θ lies is first quadrant.

II.
Question 1.
Prove that
(i) $\frac{\cos (\pi-A) \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left(\frac{3 \pi}{2}+A\right) \sin (2 \pi-A)}$ = cos A

Answer:

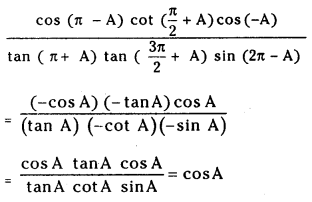
(ii) $\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}$
Answer:

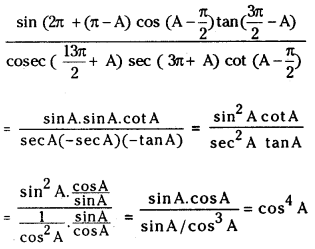
(iii) sin 780°. sin 480° + cos 240°. cos 300° = $\frac{1}{2}$
Answer:
sin [2 × 360 + 60] sin [360 + 120] + cos [180 + 60] cos [360-60]
= sin 60 sin 120 – cos 60 cos 60
= sin 60 sin 60 – cos 60. cos 60
= $\frac{\sqrt{3}}{2} \frac{\sqrt{3}}{2}-\frac{1}{2} \cdot \frac{1}{2}=\frac{3}{4}-\frac{1}{4}=\frac{1}{2}$

(iv) $\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}$ = -2
Answer:

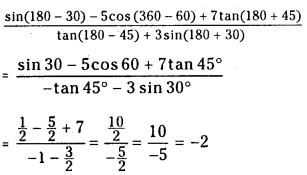
(v) cot$\left(\frac{\pi}{20}\right)$. cot$\left(\frac{3 \pi}{20}\right)$. cot$\left(\frac{5 \pi}{20}\right)$. cot$\left(\frac{7 \pi}{20}\right)$. cot$\left(\frac{9 \pi}{20}\right)$ = 1
Answer:
cot$\left(\frac{\pi}{20}\right)$. cot$\left(\frac{3 \pi}{20}\right)$. cot$\left(\frac{5 \pi}{20}\right)$. cot$\left(\frac{7 \pi}{20}\right)$. cot$\left(\frac{9 \pi}{20}\right)$
= cot 9°. cot 27°. cot 45°. cot 63°. cot 81°
= cot 9°. cot 27°. 1.cot (90 – 27) . cot (90 -9)
= cot 9°. cot 27°. 1. tan 27°. tan 9°
= 1

Question 2.
(i) Simplify $\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}$

Answer:

(ii) If tan 20 ° = p, prove that
$\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}$
Answer:
Given that tan 20° = p then

(iii) If α, β are complementary angles such that b sin α = a, then find the value of (sin α cos β – cos α sin β)
Answer:
Given α, β are complementary angles α + β = 90°
⇒ β = 90° – α
∴ sin α cos β – cos α sin β
= sin (α – β)
= sin[α – (90 – α)]
= sin [2α – 90°]
= -sin[90 – 2α]
= -cos 2α
= -(1 – 2sin²α) = -1 + 2sin²α
= -1 + 2$\left(\frac{a^2}{b^2}\right)$
= $\frac{2 a^2-b^2}{b^2}$

Question 3.
(i) If cos A = cos B = – $\frac{1}{2}$, A does not lie in the second quadrant and B does not lie in third quadrant, then find the value of $\frac{4 \sin B-3 \tan A}{\tan B+\sin A}$

Answer:
cos A = –$\frac{1}{2}$ and A does not lie in second quadrant
⇒ A lies in third quadrant
cos B = –$\frac{1}{2}$ and B does not lie in third quadrant
⇒ B lies in second quadrant
cos A = –$\frac{1}{2}$ and A lie in third quadrant
⇒ A = 240°
cos B = –$\frac{1}{2}$ and B lies in second quadrant.
⇒ B = 120°

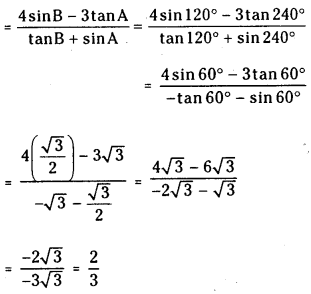
(ii) If 8 tan A = -15 and 25 sin B = -7 and neither A nor B is in the fourth quadrant, then show that sin A cos B + cos A sin B = $\frac{-304}{425}$
Answer:
8 tan A = -15 25 sin B = -7
⇒ tan A = $\frac{-15}{8}$ ⇒ sin B = $\frac{-7}{25}$
Given neither A nor B is in the fourth quadrant, clearly A is in second quadrant and B is in third quadrant,
sin A cos B + cos A sin B