TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(e)

TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(e)

I.
Question 1.
Find the adjoint and inverse of the following matrices. (March 2002)

i) $\left[\begin{array}{rr} 2 & -3 \\ 4 & 6 \end{array}\right]$
Answer:
If A = $\left[\begin{array}{ll} a & b \\ c & d \end{array}\right]$ then adj A = $\left[\begin{array}{rr} \mathrm{d} & -\mathrm{b} \\ -\mathrm{c} & \mathrm{a} \end{array}\right]$

ii) $\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]$
Answer:

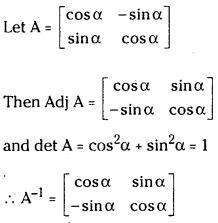
iii) Find the adjoint and inverse of the matrix $\left[\begin{array}{lll} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 3 & 2 & 1 \end{array}\right]$.
Answer:
Find cofactors of elements in the matrix as

iv) $\left|\begin{array}{lll} 2 & 1 & 2 \\ 1 & 0 & 1 \\ 2 & 2 & 1 \end{array}\right|$
Answer:

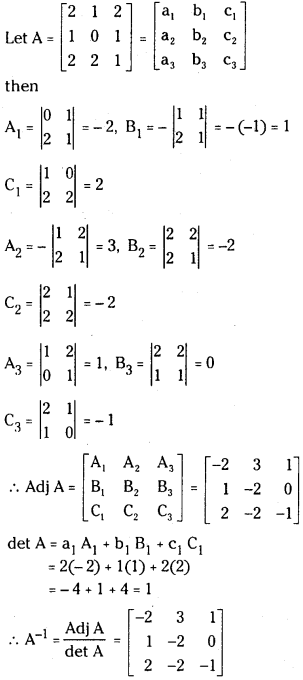
Question 2.
If A = $\left[\begin{array}{cc} \mathrm{a}+\mathrm{i b} & \mathrm{c}+\mathrm{i d} \\ -\mathrm{c}+\mathrm{i d} & \mathrm{a}-\mathrm{i b} \end{array}\right]$, a² + b² + c² + d² = 1

Answer:
det A = (a + ib) (a – ib) – (c + id) (- c + id)
= (a² – i² b²) – (- c² + i²d²)
= a² + b² + c² + d² (∵ i² = -1)
= 1
Adj A = $\left[\begin{array}{cc} a-i b & -c-i d \\ c-i d & a+i b \end{array}\right]$
A^-1 = $\frac{{Adj} A}{{det} A}=\left[\begin{array}{cc} a-i b & -c-i d \\ c-i d & a+i b \end{array}\right]$

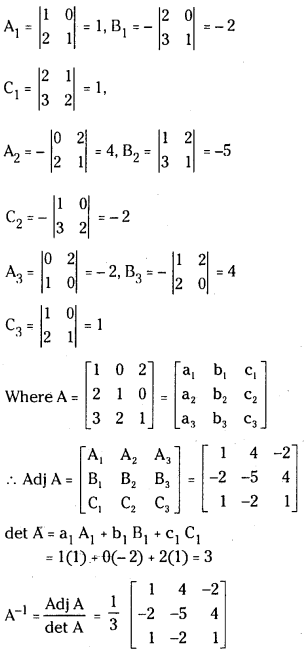
Question 3.
If A = $\left[\begin{array}{ccc} 1 & -2 & 3 \\ 0 & -1 & 4 \\ -2 & 2 & 1 \end{array}\right]$, then find (A’)^-1. (Board Model Paper)

Answer:

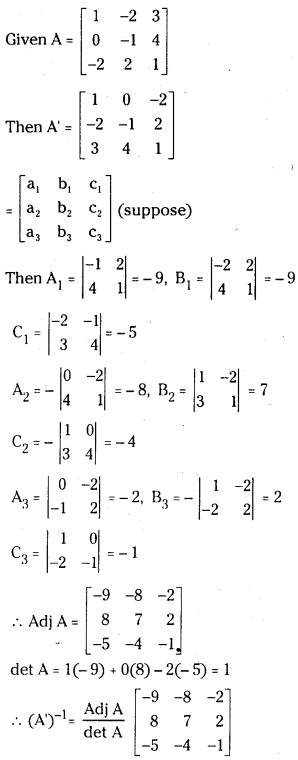
Question 4.
If A = $\left[\begin{array}{rrr} -1 & -2 & -2 \\ 2 & 1 & -2 \\ 2 & -2 & 1 \end{array}\right]$, then show that the adjoint of A = 3A, find A^-1

Answer:

Question 5.
If abc ≠ 0; find the inverse of $\left[\begin{array}{lll} \mathrm{a} & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{array}\right]$ (May 2006)

Answer:

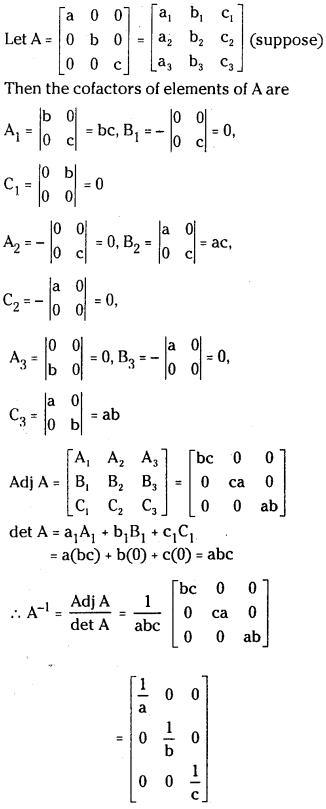
II.
Question 1.
If A = $\left[\begin{array}{lll} \mathrm{b}+\mathrm{c} & \mathrm{c}-\mathrm{a} & \mathrm{b}-\mathrm{a} \\ \mathrm{c}-\mathrm{b} & \mathrm{c}+\mathrm{a} & \mathrm{a}-\mathrm{b} \\ \mathrm{b}-\mathrm{c} & \mathrm{a}-\mathrm{c} & \mathrm{a}+\mathrm{b} \end{array}\right]$ and B = $\frac{1}{2}\left[\begin{array}{lll} \mathrm{b}+\mathrm{c} & \mathrm{c}-\mathrm{a} & \mathrm{b}-\mathrm{a} \\ \mathrm{c}-\mathrm{b} & \mathrm{c}+\mathrm{a} & \mathrm{a}-\mathrm{b} \\ \mathrm{b}-\mathrm{c} & \mathrm{a}-\mathrm{c} & \mathrm{a}+\mathrm{b} \end{array}\right]$, then show that ABA^-1 is a diagonal matrix.

Answer:

Question 2.
If 3A = $\left[\begin{array}{ccc} 1 & 2 & 2 \\ 2 & 1 & -2 \\ -2 & 2 & -1 \end{array}\right]$, then show that A^-I = A’.

Answer:

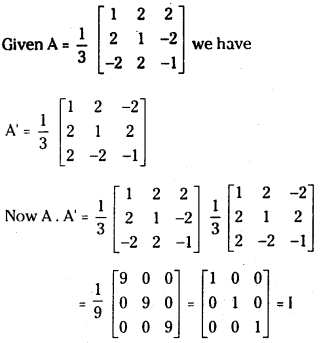
∴ A.A’ = I and by definition A’ = A^-1
similarly A’.A = I

Question 3.
If A = $\left[\begin{array}{rrr} 3 & -3 & 4 \\ 2 & -3 & 4 \\ 0 & -1 & 1 \end{array}\right]$, then show that A^-1 = A³

Answer:

So, the multiplicative inverse of A exists and it is A³.
∴ A^-1 = A³

Question 4.
If AB = I or BA = I, then prove that A is invertible and B = A^-1.
Answer:
Given AB = I
⇒ |AB| = |I|
⇒ |A| |B| = 1
⇒ |A| ≠ 0
∴ A is a non-singular matrix.
Also BA = I
⇒ |B| |A| = |I|
⇒ |A| |B| = 1
⇒ |A| *0
∴ A is a non-singular matrix.
⇒ A is invertible
⇒ A^-1 exists AB = I
⇒ A^-1 AB = A^-1I
⇒ (A^-1 A) B = A^-1I
⇒ IB = A^-1I
⇒ B = A^-1.