TS Inter 1st Year Maths 1A Solutions Chapter 2 Mathematical Induction Ex 2(a),TG Inter 1st Year Maths 1A Mathematical Induction Solutions Exercise 2(a)Using Mathematical Induction prove each of the following statement for all n ∈ N.

Question 1.
1² + 2²+ 3² + …………. + n² = n(n+1)(2n+1)/6

Answer:
Let S(n) be the given statement
1² + 2² + 3² + …………. + n² = n(n+1)(2n+1)/6
Since 1² = 1(1+1)(2+1)/6
⇒ 1 = 1; the statement is true for n = 1
Suppose the statement is true for n = k then
(1² + 2² + 3² + ………….. + k²) + k(k+1)(2k+1)/6
We have to prove that the statement is true for n = k + 1 also then
(1² + 2² + 3² + …………… + k²) + (k + 1)²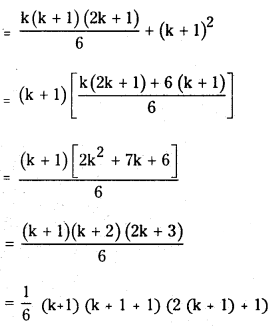

∴ The statement is true for n = k + 1 also.
∴ By the principle of Finite Mathematical Induction S(n) is true for all n ∈ N.
i.e., 1² + 2² + 3² + ……….. + n² = n(n+1)(2n+1)/6, ∀ n ∈ N

Question 2. 2.3 + 3.4 + 4.5 + ………………. upto n terms = n(n²+6n+11)/3 (March 13, May 06)

Answer:
Let S(n) be the statement.
The nth term of 2.3 + 3.4 + 4.5 + …………… is (n + 1) (n + 2)
∴ 2 . 3 + 3 . 4 + 4 . 5 + …………….. + (n + 1) (n + 2)
= n(n²+6n+11)/3
Now S(1) = 2 . 3 = 1(1²+6+11)/3 = 6
∴ The statement is true for n = 1.
Suppose that the statement is true for n = k, then 2.3 + 3.4 + 4.5 + …………….. + (k + 1) (k + 2)
= k(k²+6k+11)/3
Adding (k + 1) th term of L.H.S both sides
S(k + 1) = 2.3 + 3.4 + 4.5 + ……………. + k (k + 1) (k + 2) + (k + 2) (k + 3)

∴ S(k + 1) = 1/3 (k + 1) [k² + 2k + 1 + 6 (k + 1) + 11]
= 1/3 (k + 1) [(k + 1)2 + 6(k + 1) + 11]
∴ The statement is true for n = k + 1
So by the principle of Finite Mathematical Induction S(n) is true ∀ n ∈ N
∴ 2 . 3 + 3 . 4 + 4 . 5 + ……………. + (n + 1) (n + 2) = n(n²+6n+11)/3

Question 3. 1/1⋅3+1/3⋅5+1/5⋅7 + ……………. + 1/(2n−1)(2n+1) = n2n/+1 (May 2014)

Answer:
Let Sn be the statement
1/1⋅3+1/3⋅5+1/5⋅7 + ……………. + 1/(2n−1)(2n+1)
Then S(1) = 1/1⋅3=1/2(1)+1=1/3
∴ S(1) is true.
Suppose the statement is true for n = k, then
S(K) = 1/1⋅3+1/3⋅5+1/5⋅7+….+1(2k−1)(2k+1) = k/2k+1
We have to show that the statement is true for n = k + 1 also,

The statement S(n) is true for n = k + 1
∴ By the principle of Mathematical Induction S(n) is true for all n ∈ N.
∴ 1/1⋅3+1/3⋅5+1/5⋅7 + ……………. + 1/(2n−1)(2n+1) = n/2n+1

Question 4. 4³ + 8³ + 12³ + ………… + upto n terms = 16n² (n + 1)²

Answer:
4, 8, 12, are in A.P. and nth term of A.P. is = a + (n – 1) d
= 4 + (n – 1) 4 = 4n
Let S(n) be the statement
4³ + 8³ + 12³ + ……………… + (4n)³ = 16n² (n + 1)²
Let n = 1, then
S(1) = 4³ = 16 (1 + 1)² = 64
∴ The statement is true for n = 1 also.
Suppose the statement is true for n = k then
4³ + 8³ + 12³+ ……………… + (4k)³ = 16k² (k + 1)²
We have to prove that the result is true for n = k + 1 also. Adding (k + 1) th term
= [4 (k + 1)]³ = [4k + 4]³ both sides
4³ + 8³ + 12³ + ……………….. + (4k)³ + (4k + 4)³
= 16k³ (k + 1)2 + [4 (k + 1)]³
= 16 (k + 1)² [k² + 4k + 4]
= 16 (k + 1)² (k + 2)²
= 16 (k + 1)² [(k + 1) + 1]²
Hence the result is true for n = k + 1.
∴ By the principle of Mathematical Induction S(n) is true ∀ n ∈ N.
∴ 4³ + 8³ + 12³ + ……………….. + (4n)³ = 16n2 (n + 1)2

Question 5.
a + (a + d) + (a + 2d) + ……………… upto n terms = n/2 [2a + (n – 1) d]

Answer:
Let S(n) be the statement
a + (a + d) + (a + 2d) + + [a + (n – 1) d] = n/2 [2a + (n – 1) d]
Now S(1) is a = 1/2 [2a + 0 (d)] = a
∴ S(1) is true.
Assume that the statement is true for n = k
∴ S(k) = a + (a + d) + (a + 2d) + ……………….. + [a + (k – 1) d]
= k/2 [2a + (k – 1) d]
We have to prove that the statement is true for n = k + 1 also.
Adding a + kd both sides
a + (a + d) + ……………. + [a + (k – 1) d] + [a + kd]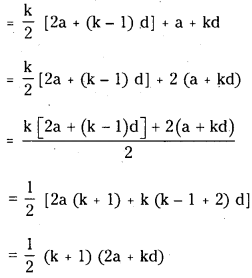

∴ The statement is true for n = k + 1 also
∴ By the principle of Mathematical Induction.
S(n) is true for all n ∈ N
∴ a + (a + d) + (a + 2d) + + [a + (n – 1) d] = n/2 [2a + (n -1) d]

Question 6.
a + ar + ar² + ………………… + n terms = a(rⁿ−1)/r−1, r ≠ 1 (March 2011)

Answer:
Let S(n) be the statement
a + ar + ar² + ………….. + arn – 1 = (rⁿ−1)/r−1, r ≠ 1
Then S(1) = a = a(r¹−1)/r−1 = a
∴ The result is true for n = 1
Suppose the statement is true for n = k then
a + ar + ar² + …………… + ar = a(r^k−1)/r−1, r ≠ 1
We have to prove that the result is true for n = k + 1 also.
Adding ark both sides
(a + ar + ar² + ………….. + ar^{k – 1} + ar^k)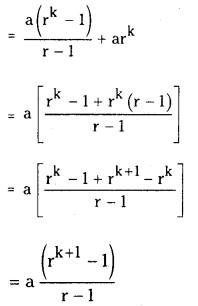

∴ The statement is true for n = k + 1 also
∴ By the principle of Mathematical Induction p(n) is true for all n ∈ N
a + ar + ar² + ………………… + n terms = a(rⁿ−1)/r−1, r ≠ 1

Question 7.
2 + 7 + 12 + ………. + (5n – 3) = n(5n−1)/2

Answer:
Let S(n) be the statement
2 + 7 + 12 + ………. + (5n – 3) = n(5n−1)/2 = 1(5−1)/2 = 2,
Since S(1) = 2,
S(1) is true.
Suppose the statement is true for n k then
(2 + 7 + 12 + ………….. + (5k – 3) = k(5k−1)/2
We have to show that S(n) is true for n = k + 1 also.
Adding (k + 1)th term 5 (k + 1) – 3 = 5k + 2 both sides
[2 + 7 + 12 + ……. + 5k – 3)] + (5k + 2)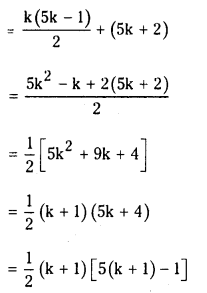

∴ S(n) is true for n = k + 1 also
∴ By the principal of Mathematical Induction
S(n) is true ∀ n ∈ N
∴ 2 + 7 + 12 + …………… + (5n – 3) = n(5n−1)/2.

Question 8.
(1 + 3/1)(1 + 5/4)(1 + 7/9)………(1 + 2n+1/n^{2) = (n + 1)2 (March 2015-A.P)}

<sup>Answer:
Let S_n be the statement

∴ S(n) is true for n = 1
Suppose Sn is true for n = k then
(1 + 3/1)(1 + 5/4)(1 + 7/9)……(1 + 2k+1/k2)
= (k + 1)2 ………………. (1)
We have to prove that the statement is true for n = k + 1 also
(k + 1) th term is

= k2 + 4k + 4
= (k + 2)2
∴ S(n) is true for n = k + 1 also
∴ By the principal of Mathematical Induction S(n) is true for ∀ n ∈ N</sup>

Question 9.
(2n + 1) < (n + 3)2

^{Answer:
Let S(n) be the statement
When n = 1, then 9 < 16 ∴ S(n) is true for n = 1 Suppose S(n) is true for n = k then(2k + 7) < (k + 3)2 …………….. (1)
We have to prove that the result is true for n = k + 1
i.e., 2(k + 1) + 7 < (k + 4)2
∴ 2 (k + 1) + 7 = 2k + 2 + 7 = (2k + 7) + 2 < (k + 3)2 + 2 (From (1))
= k2 + 6k + 9 + 2
= k2 + 6k + 11 < (k2 + 6k + 11) + (2k + 5)
= k2 + 8k + 16
= (k + 4)2
∴ S(n) is true for n = k + 1 also
By principle of Mathematical Induction
S(n) is true ∀ n ∈ N}

Question 10.
12 + 22 + ……………. + n2 > n3/3

<sup>Answer:
Let S(n) be the statement
When n = 1, then 1 > 1/3
∴ S(n) is true for n = 1
Assume S(n) to be true for n = k then
12 + 22 + ……………. + k2 > k3/3
We have to prove that the result is true for n = k + 1 also.

∴ S(n) is true for n = k + 1 also
∴ By principle of Mathematical Induction.
S(n) is true ∀ n ∈ N</sup>

Question 11.
4ⁿ – 3n – 1 is divisible by 9

Answer:
Let S(n) be the statement,
4ⁿ – 3n – 1 is divisible by 9
For n = 1, 4 – 3 – 1 = 0 is divisible by 9
∴ Statement S(n) is true for n = 1.
Suppose the statement S(n) is true for n = k
Then 4^k – 3k – 1 is divisible by 9.
∴ 4^k – 3k – 1 = 9t for t ∈ N ……………. (1)
We have to show that statement is true for n = k + 1 also.
From (1), 4^k = 9t + 3k + 1
∴ 4^{k + 1} – 3 (k + 1) – 1 = 4 . 4^k – 3 (k + 1) – 1
= 4 (9t + 3k + 1) – 3k – 3 – 1
= 4 (9t) + 9k
= 9 (4t + k) divisible by 9
(∵ 4t + k is an integer)
Hence, S(n) is true for n = k + 1 also.
∴ 4^{k + 1} – 3 (k + 1) – 1 is divisible by 9
∴ The statement is true for n = k + 1
∴ By the principle of Mathematical Induction.
S(n) is true for all n e K
∴ 4n – 3n – 1 is divisible by 9

Question 12.
3.5^{2n + 1} + 2^{3n + 1} is divisible by 17 (May 2012, 2008)

Answer:
Let Sn be the statement
3.5^{2n + 1} + 2^{3n + 1} is divisible by 17
S(1) is 3 . 5^{2(1) + 1} + 2^{3 (1)} + 1
= 3 . 5³ + 2⁴ = 3 (125) + 16
= 375 + 16 = 391 is divisible by 17
Hence, S(n) is true for n = 1.
Suppose that the statement is true for n = k, then
3.5^{2k + 1} + 2^{3k + 1} is divisible by 17 and
3.52^{k + 1} + 2^{3k + 1} = 17t for t ∈ N
then we have to show that the result is true for n = k + 1 also
Consider 3.5^{2(k + 1)} + 1 + 2^{3(k + 1)} + 1
= 3.5^{2k + 1} . 5² + 2^{3(k + 1)} . 2
= (17t – 2^{3k + 1}) 5² + 2^{3k + 3} . 2
= 17t (25) – 2^3k (50) + 2^3k (16)
= 17 t (25) + 2^3k (16 – 50)
= 17 t (25) – 34 2^3k
= 17 [25t – 2^{3k + 1}
25t – 2^{3k + 1} is an integer.
∴ 3.5^{2(k + 1)} + 1 + 2³ (k + 1) + 1 is divisible by 17.
∴ The statement S(n) is true for n = k + 1 also.
∴ By the principle of Mathematical induction S(n) is true for ∀n ∈ N
∴ 3.5^{2n + 1} + 2^{3n + 1} is divisible by 17

Question 13.
1.2.3 + 2.3.4 + 3.4.5 + ……………. upto n terms = n(n+1)(n+2)(n+3)/4. (March 2015-T.S) (Mar. 08)

Answer:
The n^th term of the given series is n (n + 1) (n + 2) and let Sn be the statement.
1.2.3 + 2.3.4 + 3.4.5 + ……………. + n (n + 1) (n + 2)
= n(n+1)(n+2)(n+3)/4
For n = 1
S(1) = 1.2.3 = 6
= 1(1+1)(1+2)(1+3)/4
= 2(3)(4)/4 = 6
∴ S(n) is true for n = 1
Let S(n) is true for n = k then
1.2.3 + 2.3.4 + 3.4.5 + ……………. + k (k + 1) (k + 2)
= k(k+1)(k+2)(k+3)/4 …………….. (1)
We have to prove that the result is true for n = k + 1 also.
Adding (k + 1) th term, (k + 1) (k + 2) (k + 3) both sides we get
1.2.3 + 2.3.4 + 3.4.5 + ……………. + k(k + 1)(k + 2) + (k + 1) (k + 2) (k + 3)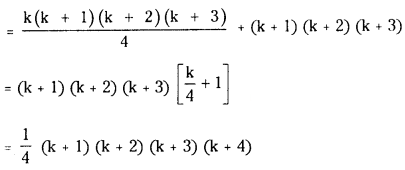

∴ S(n) is true for n = k + 1 also.
Hence by the principle of Mathematical Induction.
S(n) is true for ∀n ∈ N
∴ 1.2.3 + 2.3.4 + 3.4.5 + ……………. + n (n + 1) (n + 2) = n(n+1)(n+2)(n+3)4

Question 14.
1³/1 + 1³+2³/1+3 + 1³+2³+3³/1+3+5 + ……………… upto n terms = n/24 (2n2 + 9n + 13). (Mar. 14, 04, 05)

Answer:
The n^th term of the given series is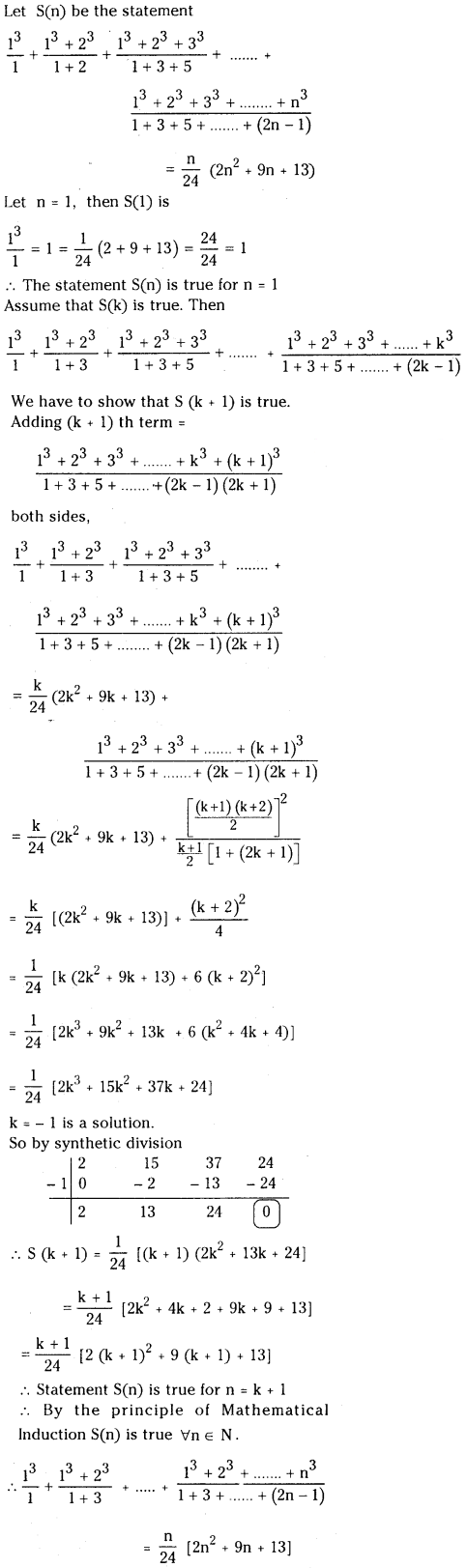

Question 15.
1² + (1² + 2²) + (1² + 2² + 3²) + ……………. upto n terms = n(n+1)²(n+2)/12. (March 2012)

Answer:
Let S(n) be the statement and
nth term of series is 1² + 2² + 3² + ……………… + n²
∴ S(n) = 1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + n²)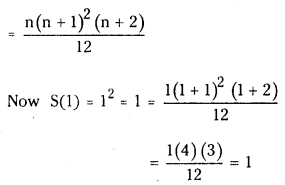

∴ S(n) is true for n = 1.
Suppose S(n) is true for n = k then
1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + k²) = k(k+1)2(k+2)/12
Now we have to prove that S(k + 1) is true.
So 1² + (1² + 2²) + (1² + 2² + 3²) + ……… + (1² + 2² + 3² + ………………. + k²) + (1² + 2² + 3² + ……………. + k² + (k + 1)²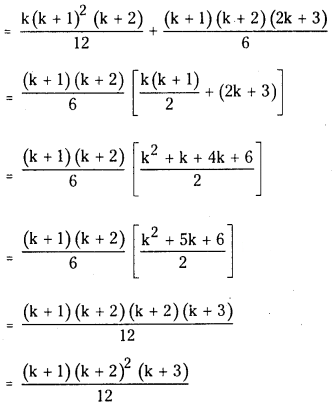

∴ The statement S(n) hold for n = k + 1 also
∴ By the principle of Mathematical Induction S(n)is true ∀n ∈ N.
∴ 1² + (1² + 2²) + (1² + 2² + 3²) + (1² + 2² + 3² + …………… + n²) = n(n+1)²(n+2)/12