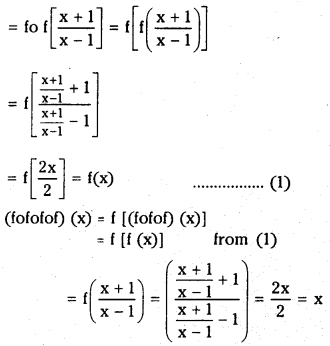TS Inter 1st Year Maths 1A Solutions Chapter 1 Functions Ex 1(b)

TS Inter 1st Year Maths 1A Functions Solutions Exercise 1(b)

I.

Question 1.
If f(x) = e^x, and g(x) = log_ex, then show that fog = gof and find f^-1 and g^-1.

Answer:
Given f(x) = ex and g(x) = log_ex
Now (fog) (x) = f[g(x)] = f [log_ex]
= e^logex = x
(gof) (x) = g [f(x)] = g [e^x] = log_ee^x = x
fog = gof
given f(x) = e^x = y
then x = f^-1 (y) and y = ex ⇒ x = log_ey
f-1(y) = logey ⇒ f^-1 (x) = log_ex
similarly y = g(x) = loge^x
then x = g^-1 (y) and y = log_ex
⇒ x = e^y
g^-1 (y) = e^y ⇒ g^-1(x) = ex

Question 2.
If f(y) = y/√1−y², g(y) = y/√1+y² then show that (fog)(y) = y.

Answer: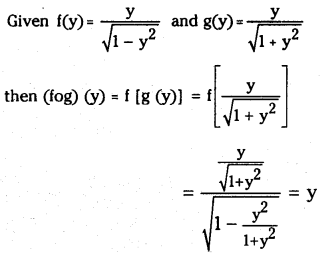

∴ (fog) (y) = y

Question 3. If R → R; g : R → R are defined by . f(x) = 2x² + 3 and g(x) = 3x – 2, then find
(i) (fog) (x)
(ii) (gof) (x)
(iii) (fof)(0)
(iv) go (fof) (3)

Answer:
f; R → R; g : R → R and
f(x) = 2x² + 3, g(x) = 3x – 2 then
(i) (fog) (x) = f [g (x)] = f (3x – 2)
= 2 [(3x – 2)²] + 3 (∵ f (x) = 2x² + 3)
= 2 [9x² – 12x + 4] + 3
= 18x² – 24x + 11
(ii) (gof) (x) = g [f (x)] = g (2x² + 3)
= 3 (2x² + 3) -2 = 6x² + 7

iii) (fof) (0) = f [f (0)] = f [3] = 2(3)² + 3 = 21

iv) go (fof) (3)
= go [f (f (3))] (v f (x) = 2x² + 3)
= go [f (2(3)² + 3)]
= go [f (21)]
= g [2 (21)² + 3]
= g [2 (441) + 3]
= g [885]
= 3 (885) – 2 = 2653 (∵ g(x) = 3x – 2)

Question 4.
If f:R → R, g:R → R are defined by f(x) = 3x – 1, g(x) = x² + 1, then find
(i) (fof) (x² + 1)
(ii) (fog) (2) (March 2012)
(iii) (gof)(2a – 3)

Answer:
Given f: R → R and g : R → R defined by f (x) = 3x – 1, g (x) = x² + 1
(i)(fof) (x² + 1 ) = f [f (x² + 1)]
= f [3 (x² + 1) – 1]
⇒ f [3x² + 2] (∵ f (x) = 3x – 1)
= 3 (3ײ + 2) – 1 = 9ײ + 5

(ii) (fog) (2) = f [g (2)] = f [2² + 1] = f [5]
= 3(5) – 1 = 14

(iii) (gof ) (2a – 3)
=g[f(2a – 3)]
= g[3(2a – 3) – 1] (∵ f(x) = 3x- 1)
= g [6a – 10]
= (6a – 10)² + 1 (∵ g(x)=x² + 1)
= 36a² – 120a + 101

Question 5.
If f(x) = 1/x, g(x) = √x ∀ x ∈ (0, ∞) then find (gof)(x).

Answer:
(gof)(x) = g[f(x)] = g[1/x]
= 1/√x (∵ g(x) = x)

Question 6.
f(x) = 2x – 1, g(x) = x+1/2 ∀ x ∈ R, find (gof)(x).

Answer:
(gof)(x) = g[f(x)] = g(2x – 1)
= 2x−1+1/2 = x (∵ g(x) = 2x−1+1/2)

Question 7.
If f(x) = 2, g(x) = x², h(x) = 2x ∀ x ∈ R, then find [fo(goh) (x)].

Answer:
fo(goh)= fog [h(x)]
= fog [2x]
= f [g(2x)]
= f [ (2x)² ] = f (4x²) = 2
∴ fo(goh) = 2

Question 8.
Find the inverse of the following functions.
(i) a, b ∈ R, f: R → R, defined by f(x) = ax + b, (a ≠ 0).

Answer:
a, b ∈ R, f : R → R and f(x) = ax + b
⇒ y = ax + b = f(x)
⇒ x = f^-1(y)
= y−b/a
∴ f-1(x) = x−b/a
(ii) f: R → (0, ∞) defined by 5^x (March 2011)
Answer:
f: R→ (0, ∞) and f(x) = 5^x
Let y = f (x) = 5^x ⇒ x = f^-1(y)
and x = log₅y
∴ f^-1(y) = log₅y ⇒ f^-1(x) = log₅x

(iii) f : (0, ∞) → R defined by f(x) = log₂x
Answer:
Gii’en f: (0, ∞) → R defined by f(x) = log₂x
Let y = f (x) = log₂x then x = f1 (y)
y = log₂x ⇒ x = 2^y
∴ f^-1(y) = 2y ⇒ f^-1(x) = 2^x

Question 9.
If f(x) = 1 + x + x² + ………….. for |x| < 1, then show that f-1(x) = x−1/x

Answer:
Given f(x) = 1 + x + x² + ………. for |x| < 1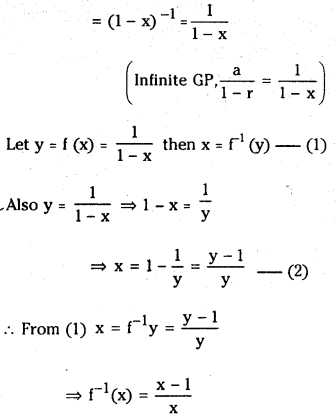

Question 10.
If f : [1, ∞] → [1, ∞] defined by f(x) = 2^{x(x – 1)}, then find f^-1(x)

Answer:
Given f : [1, ∞] → [1, ∞] defined by f(x) = 2^{x(x – 1)}
Let y = f(x) then x = f-1(y)
Also y = 2^{x(x – 1)} ⇒ x(x – 1) = log₂y
⇒ x² – x – log₂y = 0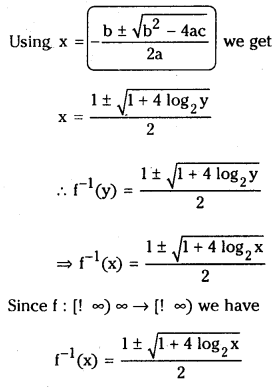

II.

Question 1.
If f(x) = x−1/x+1, x ≠ ±1, then verify (fof^-1)(x) = x

Answer:
Given f(x) = x−1/x+1, (x ≠ ±1)
and Let y = f(x) ⇒ x = f^-1(x)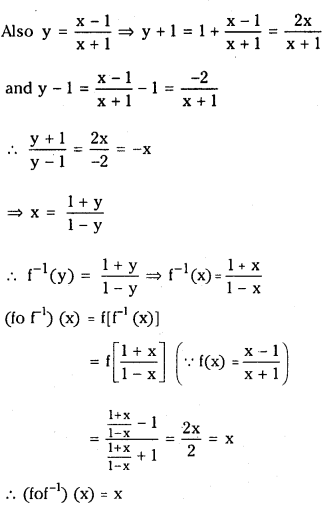

Question 2.
If A = (1, 2, 3), B = (α, β, γ), C = (p, q, r) and f : A → B, g : B → C are defined by f = {(1, α), (2, γ), (3, β)}, g = {(α, q), (β, r), (γ, p)}
then show that f and g are bijective functions and (gof)^-1 = f-1og^-1.

Answer:
Given A = {1, 2, 3}, B = (α, β, γ), c = {p, q, r) and f : A → B, g : B → C defined by f ={(1, α) (2, γ), (3, β)}and g = {(a, q), (β, r), (γ, p)}
From the definitions of f and g f (1) = α, f (2) = γ, f (3) = β and g (α) = q, g (β) = r, g (γ) = p
Distinct elements of A have distinct imagine in B. Hence f is an Injection. Also, range of f = (a, y, P) and f is a surjection.
∴ f is abijection = B similarly distinct elements of B have distinct images in c and g is an Injection.
Also range of ‘g’ = {q, γ, p} = C;
∴ g is a surjection.
Hence g is a bijection.
∴ f and g are bijective functions.
Also gof = {(1, q), (2, r), (3, p)}
and (gof-1) = {(q, 1), (r, 2), (p, 3)} …………….(1)
f-1 = {(α, 1), (γ, 2), (β, 3)}
and g-1 = {(q, α), (r, β), (p, γ)}
∴ f-1og-1 ={(q, 1), (r, 2), (p, 3)} ………………(2)
∴ From (1) and (2), (gof^-1) = f-1og^-1

Question 3.
If f:R → R; g:R → R defined by f(x) = 3x – 2, g(x) = x² + 1, then find
(i) (gof^-1) (2)
(ii)(gof)(x – 1) (March 2008, May 2006)

Answer:
Given f: R → R, g : R → R defined by f(x) = 3x – 2, g(x) = x² + 1
et y = f (x) then x = f^-1 (y)
y = 3x – 2 ⇒ 3x = y + 2
⇒ x = y+2/3
∴ f^-1(y) = 3+2/3 ⇒ f-1(x) = x+2/3
∴ (i)(gof^-1) (2) = g[f^-1(2)] = g[4/3]
= (4/3)² + 1 = 16/9 + 1 = 25/9
(ii)(gof) (x – 1) = g [f (x – 1)
= g [3 (x – 1) – 2] = g [3x – 5]
= (3x – 5)² + 1
= 9x² – 30x + 26
(∵ g(x) = x² + 1)

Question 4.
Let f = {(1, a), (2, c), (4, d), (3, b)} and g-1 = {(2, a) (4, b), (1, c), (3, d)} then show that (gof)^-1 = f^-1o g^-1

Answer:
Given f = {(1, a), (2, c), (4, d), (3, b)} and g-1 = {(2, a), (4, b), (1, c), (3, d)}
∴ g = {(a, 2), (b, 4), (c, 1), (d, 3)} gof = {(1, 2), (2, 1), (4, 3), (3, 4)}
∴ (gof)-1 = {(2, 1), (1, 2), (3, 4), (4, 3)}
f-1 = {(a, 1) (c, 2), (d, 4), (b, 3)}
g-1 = {(2, a), (4, b), (1, c), (3, d)}
f(x) = 3x – 2, g(x) = x² + 1
Let y = f (x) then x = f” (y)
∴ f^-1o g^-1 = {(2, 1), (1, 2), (4, 3), (3, 4)}
(gof)-1 = f-1o g-1

Question 5.
Let f:R → R; g:R → R be defined by f(x) = 2x – 3, g(x) = x³ + 5 then find (fog)-1(x)

Answer:
We have from the formula
(fog)^-1(x) = (g^-1of^-1) …………..(1)
where f: R → R and g : R → R are defined by
f(x) = 2x – 3 and g(x) = x³ + 5
Let y = f(x) = 2x – 3 : Then x = f^-1(y)
and 2x – 3 = y ⇒ x = y+3/2
f^-1(x)x+3/2 ………..(2)

Let y = g(x) = x³ + 5. Then x = g^-1(y) and x³ + 5 = y
⇒ x = (y – 5)^1/3
g^-1(y) = (y – 5)^1/3
g^-1(x) = (x – 5)^1/3 ……….(3)

From (1), (g^-1of^-1)(x)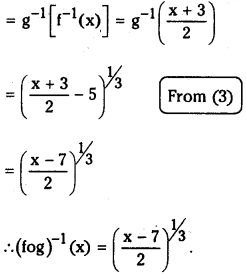

Question 6.
Let f(x) = x²,g(z) = 2^x. Then solve the equation (fog) (x) = (gof) (x)

Answer:
Given f(x) = x² and g(x) = 2^x
(fog) (x) = f [g(x)] = f [2^x] = (2^x)² = 2^2x ……………(1)
and (gof)(x) = g[f(x)] = g[x²] = 2^x2
∴ from (1) and (2), 2^2x = 2^x2
⇒ x² – 2x = 0
⇒ x(x – 2) =0
⇒ x = 0, 2

Question 7.
If f(x) = x+1/x−1,(x ≠ ±1),then find(fofof)(x) and (fofofof) (z)

Answer:
Given f(x) = x+1/x−1, (x ≠ ± 1)
then (fofof) (x) = fof(f(x)]