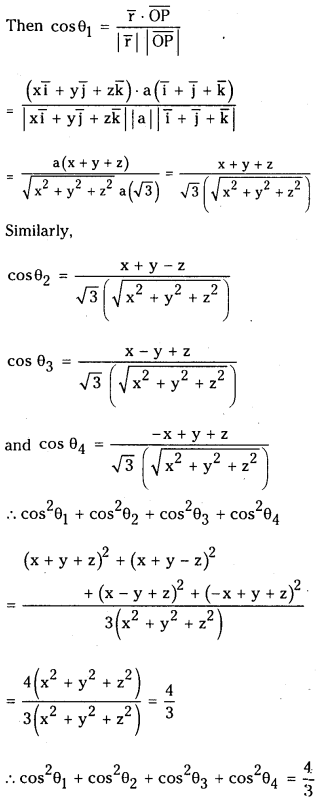TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(a)

Question 1.
Find the angle between the vectors i̅ + 2j̅ + 3k̅ and 3i̅ – j̅ + 2k̅. (Mar. ’14)

Answer:
Let a̅ = i̅ + 2j̅ + 3k̅ and b̅ = 3i̅ – j̅ + 2k̅ and θ be the angle between them. Then

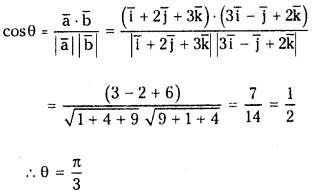
Question 2.
If the vectors 2i̅ + λ j̅ – k̅ and 4i̅ – 2j̅+ 2k̅ are perpendicular to each other then find λ. [March, May 2005]

Answer:
Let a̅ = 2i̅ + λ j̅ – k̅ and b̅ = 4i̅ – 2j̅+ 2k̅ and If a̅ is perpendicular to b̅ then a̅.b̅ = o
⇒ (2i̅ + λ j̅ – k̅).(4i̅ – 2j̅+ 2k̅) = o
⇒ 8 – 2λ – 2 = 0 ⇒ 6 – 2λ = 0 ⇒ λ = 3

Question 3.
For what values of , the vectors i̅ – j̅ + 2k̅ and 8i̅ + 6j̅ – k̅ are at right angles?

Answer:
Let a̅ = i̅ – j̅ + 2k̅ and b̅ = 8i̅ + 6j̅ – k̅
If a̅, b̅ are right angles then a̅.b̅ = o
⇒ 8 – 6λ – 2 = 0
⇒ -6λ + 6 = 0
⇒ λ = 1

Question 4.
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅. Find the vector c such that a, b and c form the sides of a triangle.

Answer:
a̅ = 2i̅ – j̅ + k̅, b̅ = i̅ – 3j̅ – 5k̅
∵ a̅, b̅, c̅ form the sides of a triangle a̅ + b̅ + c̅ = 0

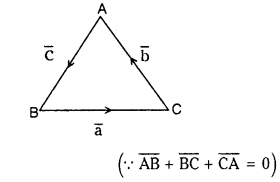
∴ c̅ = -a̅ – b̅
= -(2i̅ – j̅ + k̅) – (i̅ – 3 j̅ – 5k̅)
= -3i̅ + 4j̅ + 4k̅

Question 5.
Find the angle between the planes r̅ . (2i̅ – j̅ + 2k̅) = 3 and r̅ .(3i̅ + 6j̅ + k̅) =4 (March 2015-T.S)

Answer:
If the angle between planes

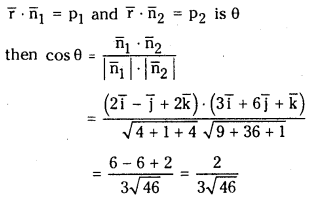
Question 6.
Let $\overline{\mathrm{e}}_1$ and $\overline{\mathrm{e}}_{\mathbf{2}}$ be unit vectors making angle θ. If $\frac{1}{2}\left|\overline{\mathrm{e}}_1-\overline{\mathrm{e}}_2\right|$ = sin λθ, then find λ.

Answer:

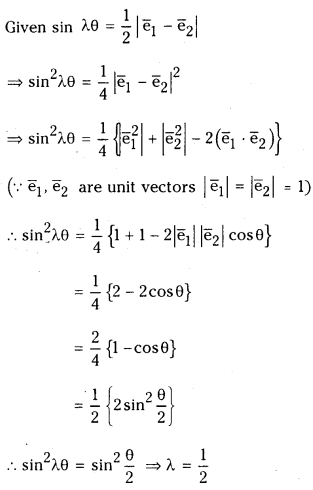
Question 7.
Let a̅ = i̅ + j̅ + k̅ and b̅ = 2 i̅ + 3j̅ + k̅. Find
(i) the projection vector of bona and its magnitude
(ii) The vector components of b̅ in the direction of a̅ and perpendicular to a̅. [May 2006]

Answer:
Orthogonal projection of a vector b̅ on a̅ is

(ii) The component vector b in the direction of –

Question 8.
Find the equation of the plane through the point (3, – 2, 1) and perpendicular to the vector (4, 7, – 4).

Answer:
The equation of the plane passing through a̅ and perpendicular to the vector n̅ is r̅. n̅ = a̅. n̅
Given n̅ = 4i̅ + 7j̅ – 4k̅ and a̅ = 3i̅ – 2j̅ + k̅
r̅ . (4i̅ + 7j̅ – 4k̅) – (3i̅ – 2j̅ + k̅) . (4i̅ + 7j̅ – 4k̅)
r . (4i̅ + 7j̅ – 4k̅) = 12 – 14 – 4 = – 6
⇒ r̅ . (-4i̅ – 7j̅ + 4k̅) = 6

Question 9.
If a̅ = 2i̅ + 2j̅ – 3k̅, b = 3i̅ – j̅ + 2k̅, then find the euigle between 2a̅ + b̅ and a̅ + 2b̅.

Answer:
Given a̅ = 2i̅ + 2j̅ – 3k̅ and b̅ = 3i̅ – j̅ + 2k̅
We have
2a̅ + b = 4i + 4j̅ – 6k̅ + 3i̅ – j̅ + 2k̅ = 7i̅ + 3j̅ – 4k̅
and a̅ + 2b̅ = (2i̅ + 2 j̅ – 3k̅) + 2(31-7 + 2k) = 8i̅ + k̅
Let ‘θ’ be the angle between the vectors 2a̅ + b̅ and a̅ + 2b̅

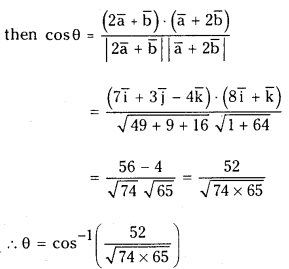
II.
Question 1.
Find the unit vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅.

Answer:
Any vector parallel to XOY plane will be of the form xi̅ + yj̅.
The vector parallel to the XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is 3i̅ + 4j̅
Its magnitudes |3i̅ + 4j̅| = $\sqrt{9+16}$ = 5
Unit vector parallel to XOY plane and perpendicular to the vector 4i̅ – 3j̅ + k̅ is
$\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{\sqrt{9+16}}\right)=\pm\left(\frac{3 \overline{\mathrm{i}}+4 \overline{\mathrm{j}}}{5}\right)$

Question 2.
If a̅ + b̅ + c̅ = 0, |a̅I|= 3, |b̅| = 5 and |c̅| = 5 then find the angle between a̅ and b̅.

Answer:
Given a̅ + b̅ + c̅ = 0
c̅ = -(a̅ + b̅)
⇒ |c̅|² = (a̅ + b̅)² = a̅² + b̅² + 2(a̅. b̅)
⇒ 49 = 9 + 25 + 2( .6)

Question 3.
If |a̅| = 2, |b̅| = 3 and |c̅| = 4 juid each of a̅, b̅, c̅ is perpendicular to the sum of the other two vectors, then find the magnitude of a̅ + b̅ + c̅.

Answer:
Given |a̅| = 2, |b̅| = 3 and |c̅| = 4
Since each of a̅, b̅, c̅ is perpendicular to the sum of other two vectors i.e., a̅ is perpendicular to b̅ + c̅
a̅ . (b̅ + c̅) = 0 ⇒ a̅ . b̅ + a̅ . c̅ = 0
Similarly
b̅.(c̅ + a̅) = 0 ⇒ b̅.c̅ + b̅.a̅ = 0
and c-(a + b) = 0 ⇒ c̅. a̅ + c̅. b̅ = 0 Adding we get
2 [(a̅ . b̅) + (b̅ . c̅) + (c̅ . a̅)] = 0 …….(1)
Also (a̅ + b̅ + c̅)
= |a̅|² + |b̅|² + |c̅|² + 2(a̅.b̅ + b̅.c̅ + c̅.a̅)
= 4 + 9 + 16 + 2(a̅.b̅ + b̅. c̅ + c̅.a̅)
= 4 + 9 + 16 + 2 (0) = 29
∴ |a̅ + b̅ + c̅| = $\sqrt{29}$

Question 4.
Find the equation of the plane passing through the point a̅ = 2i̅ + 3j̅ – k̅ and perpendicular to the vector 3i̅ – 2j̅ – 2k̅ and the distance of this plane from the origin.

Answer:
Equation of the plane passing through the point a, and perpendicular to the vector n̅ is (r̅ – a̅) . n̅ = 0
⇒ 7 . n̅ = a̅ . n̅
(liven a̅ = 2i̅ + 3 j̅ – k̅ and n̅ = 3i̅ – 2j̅ – 2k̅
We have r̅ . (3 i̅ – 2 j̅ – 2k̅)
= (2i̅ + 3j̅ – k̅) . (3i̅ – 2j̅ – 2k̅)
= 6 – 6 + 2 = 2
⇒ r̅ . (3i̅ – 2j̅ – 2k̅) = 2
The distance from origin to this plane is

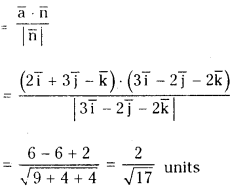
Question 5.
a̅, b̅, c̅ and d̅ are the position vectors of four coplanar points such that (a̅ – d̅) . (b̅ – c̅) = (b̅ – d̅) . (c̅ – a̅) = 0. Show that the point d represents the orthocentre of the triangle with a̅, b̅ and c̅ as its vertices.

Answer:

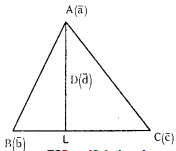
Position vectors of A, B, C, D are a̅, b̅, c̅, d̅ respectively.
$\overline{\mathrm{DA}}=\overline{\mathrm{OA}}-\overline{\mathrm{OD}}$ = a̅ – d̅
$\overline{\mathrm{CB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OC}}$ = b̅ – c̅
$\overline{\mathrm{DB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OD}}$ = b̅ – d̅
$\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}$ = c̅ – a̅
Given (a̅ – d̅) . (b̅ – c̅) = 0
⇒ $\overline{\mathrm{DA}} \cdot \overline{\mathrm{CB}}$ = 0
⇒ $\overline{\mathrm{DA}}$ is perpendicular to $\overline{\mathrm{BC}}$
∴ $\overline{\mathrm{AD}}$ is an altitude of ΔABC
and (b̅ – d̅) . (c̅ – a̅) = 0
⇒ $\overline{\mathrm{DB}} \cdot \overline{\mathrm{AC}}$ = 0
⇒ $\overline{\mathrm{DB}}$ is perpendicular to $\overline{\mathrm{AC}}$
$\overline{\mathrm{DB}}$ another altitude ΔABC
Altitudes AD and BD intersect at D
D(d) is the orthocentre of ΔABC.

III.
Question 1.
Show that the points (5, – 1, 1), (7, – 4, 7), (1,-6, 10) and (- 1, – 3, 4) are the vertices of a rhombus. (March 2013)

Answer:
Let A (5,-1, 1), B (7,-4, 7), C (1,-6, 10) and D (- 1, – 3, 4) are the given points.

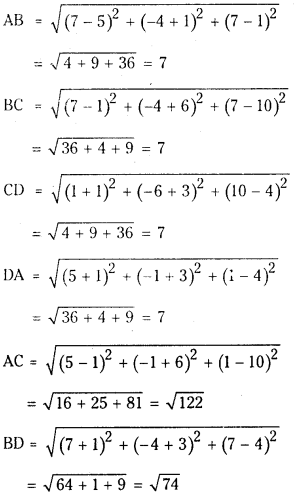
∴ AB = BC = CD = DA = 7 units and AC ≠ BD
∴ A, B, C, D are the points which are the vertices of a rhombus.

Question 2.
Let a̅ = 4i̅ + 5j̅ – k̅, b̅ = i̅ – 4j̅ + 5k̅ and c̅ = 3i̅ + j̅ – k̅. Find the vector which is perpendicular to both a and b and whose magnitude is twenty one times the magnitude of c̅.

Answer:
Given a̅ = 4 i̅ + 5 j̅ – k̅
b̅ = i̅ – 4 j̅ + 5k̅
and c̅ = 3 i̅ + j̅ – k̅
Let r̅ = xi̅ + yj̅ + zk̅ be the vector which is perpendicular to both a and b.
Then r̅. a̅ = 0 and r̅.b̅ = 0
⇒ 4x + 5y – z = 0 …………..(1)
and x – 4y + 5z = 0 ……….(2)

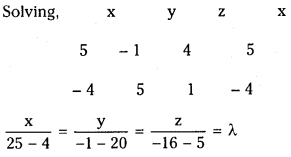
⇒ x = λ, y = -λ, z = -λ
∴ The vector which is perpendicular to both a̅ and b̅ is r̅ = λ(i̅ – j̅ – k̅)
Magnitude of c = $\sqrt{9+1+1}=\sqrt{11}$
∴ The vector which is perpendicular to both a̅ and b̅ whose magnitude is 21 times the
magnitude of c̅ is = ± $\frac{21 \sqrt{11}(\bar{i}-\bar{j}-\bar{k})}{|\bar{i}-\bar{j}-\bar{k}|}$
= ± 7$\sqrt{33}$ (i̅ – j̅ – k̅)

Question 3.
G is the centroid of ΔABC and a̅, b̅, c̅ are the lengths of the sides $\overline{\mathrm{B C}}, \overline{\mathrm{C A}}$ and $\overline{\mathrm{AB}}$ respectively. Prove that $\bar{a}^2+\bar{b}^2+\bar{c}^2=3\left(\overline{\mathrm{OA}}^2+\overline{\mathrm{OB}}^2+\overline{\mathrm{OC}}^2\right)-9(\overline{\mathrm{OG}})^2$. where ‘O’ is any point.

Answer:
Given that $\overline{\mathrm{BC}}=\overline{\mathrm{a}}, \overline{\mathrm{CA}}=\overline{\mathrm{b}}$ and $\overline{\mathrm{AB}}=\overline{\mathrm{c}}$.
Let O’ be the origin and let p.q.r be the position vectors of A, B, C then $\overline{\mathrm{OA}}=\overline{\mathrm{p}}$, $\overline{\mathrm{OB}}=\overline{\mathrm{q}}, \quad \overline{\mathrm{OC}}=\overline{\mathrm{r}}$ respectively.
Then the position vector of centroid

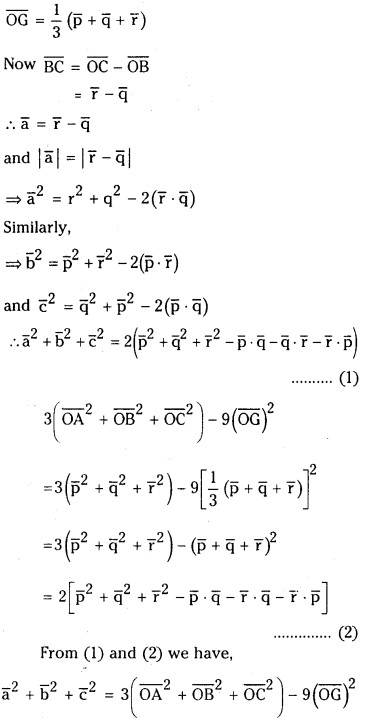
Question 4.
A line makes angles θ₁, θ₂, θ₃, and θ₄ with the diagonals of a cube. Show that cos²θ₁ + cos²θ₂ + cos²θ₃ + cos²θ₄ = $\frac{4}{3}$.

Answer:

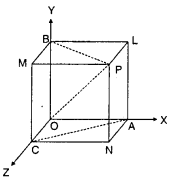
Let ‘O’ be the origin and ‘a’ be the length of the side of a cube.
i̅, j̅, k̅ are unit vectors along X, Y and Z axes respectively.

Let r̅ = xi̅ + yj̅ + zk̅ be the line makes angles θ₁, θ₂, θ₃, θ₄ with diagonals of a cube