TS Inter 1st Year Maths 1A Matrices Solutions Exercise 3(i)

Question 1.
2x + 3y – z = 0,
x – y – 2z = 0,
3x + y + 3z = 0

Answer:
The coefficient matrix obtained from the given equations is

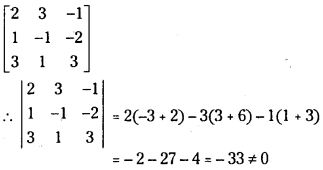
Since the determinant of the coefficient matrix ≠ 0 the system has a trivial solution, x = y = z = 0 and ρ(A) = 3.

Question 3.
x + y – 2z = 0,
2x + y – 3z = 0,
5x + 4y – 9z = 0

Answer:
The coefficient matrix is
A = $\left[\begin{array}{lll} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{array}\right]$
and $\left|\begin{array}{lll} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{array}\right|$
= 1(-9 + 12) – 1(-18 + 15) – 2
= 3 + 3 – 6 = 0
If $\left[\begin{array}{ll} 1 & 1 \\ 2 & 1 \end{array}\right]$ is any submatrix of order 2 x 2 and
$\left|\begin{array}{ll} 1 & 1 \\ 2 & 1 \end{array}\right|$ = 1 – 2 = -1 ≠ 0, ρ(A) < 3. Hence the system has a nontrival solution.

∴ System of equations is equivalent to
x + y – 2z = 0 and y – z = 0
Let z = k then y = k and x = k
∴ x = y = z = k for a real number k.

Question 4.
x + y – z= 0
x – 2y + z = 0
3x + 6y – 5z = 0

Answer:
Coefficient matrix
A = $\left[\begin{array}{ccc} 1 & 1 & -1 \\ 1 & -2 & 1 \\ 3 & 6 & -5 \end{array}\right]$
|A| = 1(10 – 6) – 1(-5 – 3) – 1(6 + 6)
= 4 + 8 – 12 = 0

∴ If $\left[\begin{array}{cc} 1 & 1 \\ 1 & -2 \end{array}\right]$ is a submatrix of order 2 and
$\left|\begin{array}{cc} 1 & 1 \\ 1 & -2 \end{array}\right|$ = -3 ≠ 0, ρ(A) = 2. System has a non-trivial solution ρ(A) < 3.
A = $\left[\begin{array}{rrr} 1 & 1 & -1 \\ 1 & -2 & 1 \\ 3 & 6 & -5 \end{array}\right]$
Use R₂ – R₁ and R₃ – 3R₁
A – $\left[\begin{array}{rrr} 1 & 1 & -1 \\ 0 & -3 & 2 \\ 0 & 3 & -2 \end{array}\right]$
System of equations is equivalent to x + y – z = 0
3y – 2z = 0
Let z = k, then 3y = 2k
⇒ y = $\frac{2 \mathrm{k}}{3}$
x = -y + z = –$\frac{2 \mathrm{k}}{3}$ + k = $\frac{k}{3}$
x = $\frac{k}{3}$, y = $\frac{2 \mathrm{k}}{3}$, z = k
for any real number of k.