NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities

Linear Inequalities Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities All Exercises were prepared by Experienced LearnCBSE.in Teachers.

Free download NCERT Solutions for Class 11 Maths Chapter 6 Linear Inequalities Ex 6.1, Ex 6.2, Ex 6.3 and Miscellaneous Exercise PDF in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.1

Ex 6.1 Class 6 Maths Question 1:

Solve 24x < 100, when (i) x is a natural number (ii) x is an integer

Ans:

The given inequality is 24x < 100.

(i) It is evident 1, 2, 3, nd 4 are the only natural numbers less than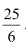

Thus, when x is a natural numbers, the solutiona of the given inequality are 1, 2, 3 and 4.

Hence, in this case, the solution set is {1, 2, 3, 4}.

(ii) The integers less than 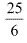are....-3, -2, -1, 0, 1, 2, 3, 4.

Thus, when x is an integer, the solutioins of the given inequality are ....-3, -2, -1, 0, 1, 2, 3, 4.

Hence, in this case, the solution set is {...-3, -2, -1, 0, 1, 2, 3, 4}.

Ex 6.1 Class 6 Maths Question 2:

Solve -12x > 30, when

(i) x is a natural numbers (ii) x is an integer

Ans:

The given inequality is -12x > 30.

(i) There is no natural numbers less than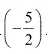

Thus, when x is natural numbers, there is no solution of the given inequality

(ii) The integers less than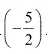 are ..., -5, -4, -3.

Thus, when x is an integer, the solutions of the given inequality are..., -5, -4, -3.

Hence, in the case, the solution set is {..., -5, -4, -3}.

Ex 6.1 Class 6 Maths Question 3:

Solve 5x - 3 < 7, when

(i) x is an integer (ii) x is real number

Ans:

The given inequalty is 5x - 3 < 7

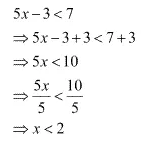
(i) The integers less than 2 are...,-4, -3, - 2,-1, 0,1.

Thus when x is an integrer, the solutions of the given inequality are

...,-4, -3, - 2,-1, 0,1.

Hence, in this case, the solution set is {...,-4, -3, - 2,-1, 0,1}

(ii) When x is a real number, the soulution of the given inequality are is, all real numbers x which are less than 2

Thus, the solution of the given inequality is x

Ex 6.1 Class 6 Maths Question 4:

Solve 3x + 8 > 2, when

(i) x is an integer (ii) x is a real number

Ans

The given inequality is 3x + 8 > 2

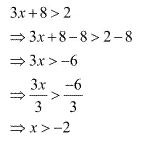
(i) The integers greater then - 2 are - 1, 0, 1, 2,...

Thus when x is an integer, the solutions of given inequality are - 1, 0, 1, 2,...

Hence, in this case, the solution set is { - 1, 0, 1, 2,...}

(ii) When x is a real number, the solutions of given inequality are all the real numbers, which are greater then - 2

Thus, in this case, the solution set is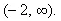

NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.2

Ex 6.2 Class 6 Maths Question 1:

Solve the given inequlity graphically in two-dimensional plane: x + y < 5

Ans:

The graphical represention of x + y = 5 is given as dotted line in the figure below

This line divides the xy-plane in two half planes, I and II

Select a point (not on the line), which line in one of the helf planes, to determine whether the point satisfies the given inquality or not

We select the point as (0,0)

It is observed that

0 + 0 < 5 or, 0 < 5, which is true

Therefore, half plane II is not the soulution of the given inequality. Also, it is evident that any point on the line does not satisfy the given strict inequality

Thus, the solution region of the given inequality is the shaded plane I excluding the point on the line.

This can be represented as follows.

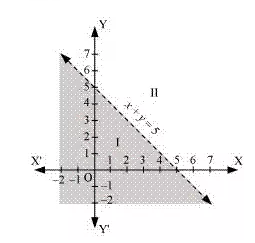
Ex 6.2 Class 6 Maths Question 2:

Solve the given inequlity graphically in two-dimensional plane: 2x + y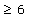

Ans:

The graphical represention of 2x + y = 6 is given as dotted line in the figure below

This line divides the xy-plane in two half planes, I and II

Select a point (not on the line), which line in one of the helf planes, to determine whether the point satisfies the given inquality or not

We select the point as (0,0)

It is observed that

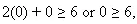which is false

Therefore, half plane II is not the soulution of the given inequality. Also, it is evident that any point on the line does not satisfy the given strict inequality

Thus, the solution region of the given inequality is the shaded plane I excluding the point on the line.

This can be represented as follows.

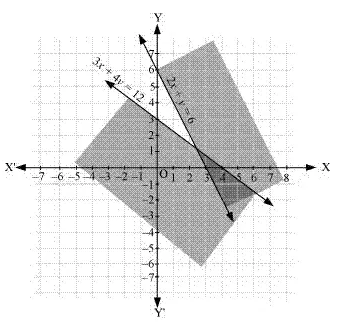
Ex 6.2 Class 6 Maths Question 3:

Solve the given inequlity graphically in two-dimensional plane: 3x + 4y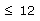

3x + 4y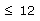

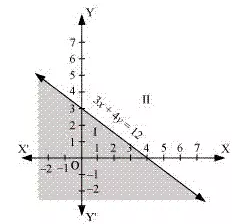
The graphical represention of 3x + 4y = 12 is given as dotted line in the figure below

This line divides the xy-plane in two half planes, I and II

Select a point (not on the line), which line in one of the helf planes, to determine whether the point satisfies the given inquality or not

We select the point as (0,0)

It is observed that

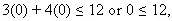which is true

Therefore, half plane II is not the soulution of the given inequality. Also, it is evident that any point on the line does not satisfy the given strict inequality

Thus, the solution region of the given inequality is the shaded plane I excluding the point on the line.

This can be represented as follows.

NCERT Solutions for Class 11 Maths Chapter 6 Exercise 6.3

Ex 6.3 Class 6 Maths Question 1:

Solve the following system of inequalities graphically: x ≥ 3, y ≥ 2

Ans:

x ≥ 3...(1)

y ≥ 2...(2)

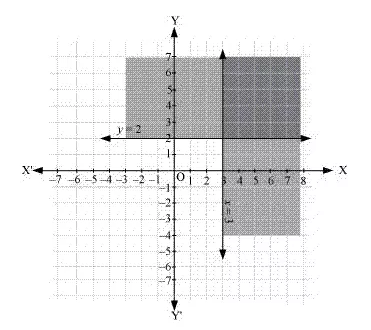
The graph of the lines, z = 3 and y = 2, are drawn in the figure below.

Inequality (1) represents the region on the right hand side of the line, x = 3 (including the line x = 3), and inequality (2) represents the region above the line, y = 2 (including the line y = 2).

Hence, the solution the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

Ex 6.3 Class 6 Maths Question 2:

Solve the following system of inequalities graphically: 3x + 2y ≤ 12, x ≥ 1, y ≥ 2

Ans:

3x + 2y ≤ 12...(1)

x ≥ 1...(2)

y ≥ 2...(3)

The graph of the lines, 3x +2y = 12,x = 1, and y = 2, are drawn in the figure below.

Inequality (1) represents the region below the line,3x + 2y = 12 (including the line 3x +2y = 12). Inequality (2) represents the region on the right side the line, x = 1 (including the line y = 1). Inequality (3) repesents the region above the line, y = 2 (including the line y = 2).

Hence, the solution the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

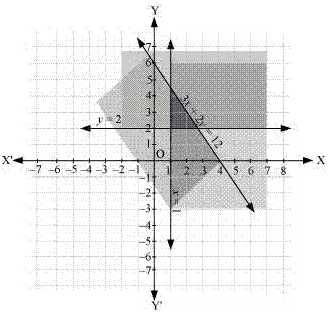
Ex 6.3 Class 6 Maths Question 3:

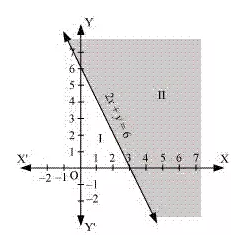
Solve the following system of inequalities graphically: 2x + y ≥ 6, 3x + 4y ≤ 12

Ans:

2x + 2y ≥ 6...(1)

3x + 4y ≤ 12...(2)

The graph of the lines, 2x +y = 6, and 3x + 4y = 12, are drawn in the figure below.

Inequality (1) represents the region above the line, 2x + y = 6 (including the line 2x +y = 6), and inequality (2) represents the region below the line, 3x + 4y = 12 (including the line 3x + 4y = 12).

Hence, the solution the given system of linear inequalities is represented by the common shaded region including the points on the respective lines as follows.

NCERT Solutions for Class 11 Maths Chapter 6 Miscellaneous Solutions

Miscellaneous Exercise Class 11 Maths Question 1:

Solve the inquality 2 ≤ 3x - 4 ≤ 5

Ans:

2 ≤ 3x - 4 ≤ 5

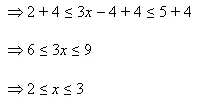
Thus, all the real numbers, x, which are greater or equal to 2 but less than or equal to 3, are the solutions of the given inequality. The solution set for the given inequality is [2,3].

Miscellaneous Exercise Class 11 Maths Question 2:

Solve the inquality 6 ≤ 3(2x - 4) < 12

Ans:

6 ≤ - 3(2x - 4) < 12

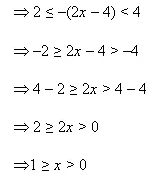
thus, the solution set for given inequality is [0,1]

Miscellaneous Exercise Class 11 Maths Question 3:

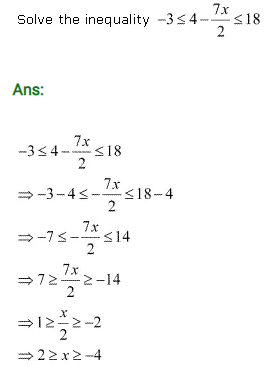
thus, the solution set for given inequality is [-4,2].