NCERT Maths Solutions Class 11th Chapter 7 Permutation and Combinations
NCERT Solutions Class 11 Maths Permutations and Combinations PDF
Download our free PDF of NCERT Solutions for Class 11 Maths Chapter 7 - Permutations and Combinations from www.manabadi.co.in. This resource includes all the questions from the NCERT books, prepared by expert mathematics teachers in accordance with CBSE NCERT guidelines. Use this PDF to enhance your preparation for board and competitive exams and boost your scores.
NCERT Solutions for Class 11 Maths Chapter 7 Exercise.7.1
Ex 7.1 Class 11 Maths Question-1
How many 3 - digit numbers can be formed from the digit 1, 2, 3, 4 and 5 assuming that
(i) repetition of the digits is allowed?
(ii) repetition of the digits is not allowed?
Ans:(i)
There will be as many ways as there are ways of filling 3 vacant places
 in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
in succession by the given five digits. In this case, repetition of digits is allowed. Therefore, the units place can be filled in by any given five digits. Similarly, tens and hundreds digits can be filled in by any of the given five digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed from the given digits is 5 x 5 x 5 = 125
(ii)
In this case, repetition of digts is not allowed. here, if units place is filled in first, then it can be filled by any of the given five digits. Therefore, the number of ways of filling the units place of the three-digit number is 5.
Then, the tens place can be filled with any of the remaining four digits and the hundreds place can be filled with any of the remaniing three digits.
Thus, by the multiplication principle, the number of ways in which three-digit numbers can be formed without repeating the given digits is 5 x 4 x 3 = 60
Ex 7.1 Class 11 Maths Question-2
How many 3 - digit even numbers can be formed from the digit 1, 2, 3, 4, 5, 6 if the digits can be repeated?
Ans:There will be as many ways as there are ways of filling 3 vacant places
 in succession by the given six digits. In this case, the units place can be filled in by 2 or 4 or 6 only i.e., the units place can be filled in 3 ways. The tens place can be filled by any of the 6 digits in 6 different ways and also the hundreds place can be filled by any of the 6 digits in 6 different ways, as the digits can be repeated.
in succession by the given six digits. In this case, the units place can be filled in by 2 or 4 or 6 only i.e., the units place can be filled in 3 ways. The tens place can be filled by any of the 6 digits in 6 different ways and also the hundreds place can be filled by any of the 6 digits in 6 different ways, as the digits can be repeated.
Therefore, by multiplication principle, the required number of three digit even numbers is 3 x 6 x 6 = 108
Ex 7.1 Class 11 Maths Question-3
How many 4- letter code can be formed using the first 10 letters of the English alphabet, if no letter can be repeated?
Ans:There are as many codes as there are ways of filling 4 vacant places  in succession by the first 10 letters of the English alphabet, keeping in mind that the repetition of letters is not allowed.
in succession by the first 10 letters of the English alphabet, keeping in mind that the repetition of letters is not allowed.
The first place can be filled in 10 different ways by any of the first 10 letters of the English alphabet follewing which, the second place can be filled in by any of the remaining letters in 9 different ways. The third place can be filled in by any of the remaining 8 letters in 8 different ways and the fourth place can be filled in by any of the remaining 7 letters in 7 different ways.
Therefore, by multiplication principle, the required numbers of ways in which 4 vacant places can be filled is 10 x 9 x 8 7 = 5040
Hence, 5040 four-letter codes can be formed using the first 10 letters of the English alphabet, if no letter is repeated
NCERT Solutions for Class 11 Maths Chapter 7 Exercise.7.2
Ex 7.2 Class 11 Maths Question-1
Evaluate
(i) 8! (ii) 4! - 3!
Ans:(i) 8! = 1 x 2 x 3 x 4 x 5 x 6 x 7 x 8 = 40320
(ii) 4! = 1 x 2 x 3 x 4 = 24
3! = 1 x 2 x 3 = 6
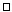 4! - 3! = 24 - 6 = 18
4! - 3! = 24 - 6 = 18
Ex 7.2 Class 11 Maths Question-2
Is 3! + 4! = 7!?
Ans:3! = 1 x 2 x 3 = 6
4! = 1 x 2 x 3 x 4 = 24
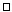 3! + 4! = 6 + 24 = 30
3! + 4! = 6 + 24 = 30
7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 = 5040
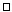 3! + 4! ≠ 7!
3! + 4! ≠ 7!
Ex 7.2 Class 11 Maths Question-3
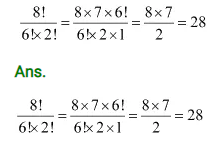
Ex 7.2 Class 11 Maths Question-4
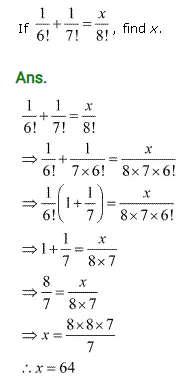
NCERT Solutions for Class 11 Maths Chapter 7 Exercise.7.3
Ex 7.3 Class 11 Maths Question-1
How many 3-digit numbers can be formed by using the digits 1 to 9 if no digit is repeated?
Ans:3 - digit numbers have to be formed using the digit 1 to 9.
Here, the order of the digits matters.
Therefore, there will be as many 3 - digit numbers as there are permutations of 9 different digits taken 3 at a time.
Therefore, required number of 3 - digit numbers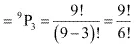
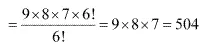
Ex 7.3 Class 11 Maths Question-2
How many 4-digit numbers are there with no digit repeated?
Ans:The thousands place of the 4-digit number is to be filled with any of the digits from 1 to 9 as the digit 0 cannot be included. Therefore, the number of ways in which thousands place can be filled is 9.
The hundreds, tens, and units place can be filled by any of the digits from 0 to 9. However, the digits cannot be repeated in the 4-digit numbers and thousands place is already occupied with a digit. The hundreds, tens, and units place is to be filled by the remaining 9 digits.
Therefore, there will be as many such 3-digit numbers as there are permutations of 9 different digits taken 3 at a time.
Number of such 3-digit numbers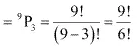
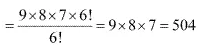
Thus, by multiplication principle, the required number of 3-digit numbers is 3 x 20 =60
NCERT Solutions for Class 11 Maths Chapter 7 Exercise.7.4
Ex 7.4 Class 11 Maths Question-1
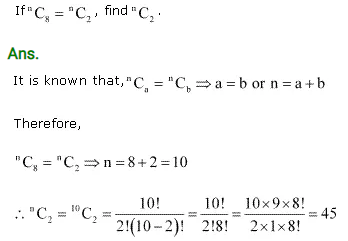
Ex 7.4 Class 11 Maths Question-2
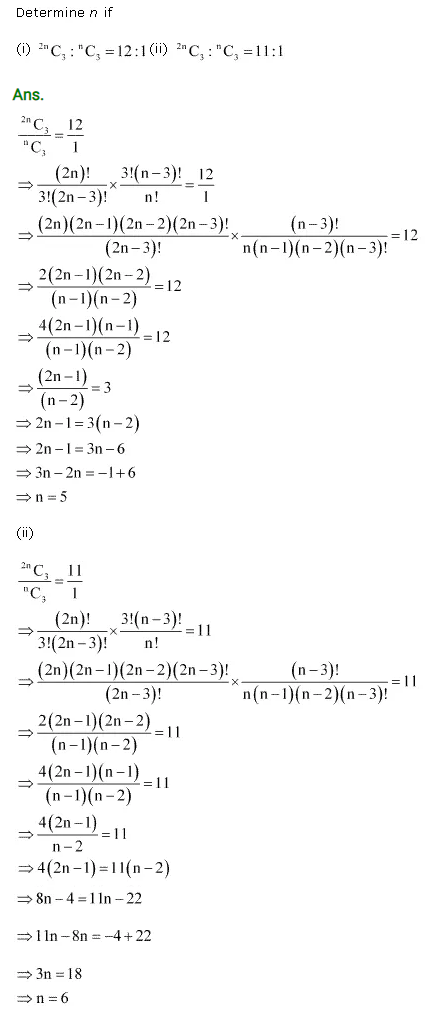
Ex 7.4 Class 11 Maths Question-3

NCERT Solutions for Class 11 maths Chapter Miscellaneous Solutions
Miscellaneous Question-1
How many words, with or without meaning, each of 2 vowels and 3 consonants can be formed from the letters of the word DAUGHTER?
Ans:In the word DAUGHTER, there arre 3 vowels namely, A, U, and E, and 5 consonants namely D, G, H, T, and R.
Number of ways of selecting 2 vowels out of 3 vowels = 3C2 = 3
Numbers of ways of selecting 3 consonant out of 5 consonants 5C3 = 10
Therefore, numbers of combinations of 2 vowel and 3 consonants = 3 x 10 = 30
Each of these 30 combinations of 2 vowels and 3 consonants can be arranged among themselves in 5! ways.
Hence, required number of different words = 30 x 5! = 3600
Miscellaneous Question-2
How many words, with or without meaning, can be formed using all the letters of the word EQUATION at a time so that the vowels and consonants occur together?
Ans:In the word EQUATION, there arre 5 vowels namely, A, E, I, O, and U, and 3 consonants namely Q, T, and N.
Since all the vowels and consonants have to occur together, both (AEIOU) and (QTN) can be assumed as single objects. then, the permutations of these 2 objects taken all at a time are counted. this number would be 2P2 = 2!
Corresponding to each of these permutations, these are 5! permurations of the five vowels taken all at time and 3! permutations of the 3 consonants taken all at a time.
Hence, by multiplication principle, required number of different words = 2! x 5! x 3! = 1440
