NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 10: Conic Sections, available in both English and Hindi Medium, updated for the CBSE term exams 2024-25. Access the revised solutions for Chapter 10 of Class 11 Mathematics, based on the rationalized textbooks and the updated syllabus for the academic year 2024-25.

NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.1

Ex 11.1 Class 11 NaQuestion 1

Find the equation of the circle with centre (0, 2) and radius 2

Ans:

The equation of the circle with center (h, k) and radius r is given as

(x – h)² + (y - k) ² = r ²

It is given that centre (h, k) = (0, 2) and radius (r) =2.

Therefore, the equation of the circle is

(x - 0) ² + (y - 2) ² = 2²

x² +y² + 4 – 4y = 4

x² + y² - 4y = 0

Ex 11.1 Class 11 NaQuestion 2

Find the equation of the circle with centre (-2, 3) and radius 4

Ans:

The equation of the circle with center (h, k) and radius r is given as

(x – h)² + (y - k) ² = r ²

It is given that centre (h, k) = ( -2, 3) and radius (r) =4.

Therefore, the equation of the circle is

(x +2) ² + (y - 3) ² =(4) ²

x² + 4x + 4 + y² - 6y + 9 = 16

x² + y² + 4x – 6y – 3 = 0

NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.2

Ex 11.2 Class 11 NaQuestion 1

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y² = 12x

Ans:

The given equation is y² = 12x

Here, the comparing of x is positive. Hence, the parabola opens towards the right.

On comparing this eqution with y ₂ = 4ax, we obtain

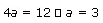
Coordinates of the focus – (a, 0) = (3, 0)

Since the given equation involves y ² , the axis of the parabola is the x – axis.

Equation of direcctrix, x = a I,e, x = - 3 I , e, x + 3 = 0

Length of latus rectum = 4a = 4 x 3 = 12

Ex 11.2 Class 11 NaQuestion 2

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x² = 6y Ans:

The given equation is x² = 6y.

Here, the comparing of y is positive. Hence, the parabola opens upwards.

On comparing this eqution with x ₂ = 4ax, we obtain

Ex 11.2 Class 11 NaQuestion 3

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for y² = 8x

Ans:

The given equation is y² = - 8x.

Here, the coefficient of x is negative. Hence, the parabola opens towards the left.

On comparing this equation with y² = -4ax, we obtain

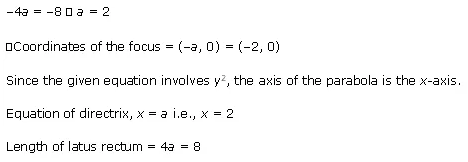
Ex 11.2 Class 11 NaQuestion 4

Find the coordinates of the focus, axis of the parabola, the equation of directrix and the length of the latus rectum for x² = 16y

Ans:

The given equation is x² = - 16y.

Here, the coefficient of x is negative. Hence, the parabola opens downwards.

On comparing this equation with x₂ = -4ay, we obtain

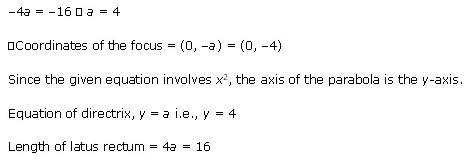
NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.3

Ex 11.3 Class 11 NaQuestion 1

Ex 11.3 Class 11 NaQuestion 2

Ex 11.3 Class 11 NaQuestion 3

NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.4

Ex 11.4 Class 11 NaQuestion 1

Ex 11.4 Class 11 NaQuestion 2

Class 11 Maths NCERT Solutions – Miscellaneous Questions

Miscellaneous Exercise class 11 Maths Question 1:

If a parabolic reflector is 20 cm diameter and 5 cm deep, find the focus.

Ans:

The origin of the coordinate plane is taken at the vertex of the parabolic reflector in such a way that axis of the reflector is along the positive x – axis.

This can be diagrammatically represented as

Miscellaneous Exercise class 11 Maths Question 1:

An arch in the form of parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Ans:

The origin of the coordinate plane is taken at the vertex of the arch in such a way that its vertical axis is along the positive y- axis

This can be diagrammatically represented as