MCQ Questions for Class 10 Maths Quadratic Equations with Answers
MCQ Questions for Class 10 Maths Quadratic Equations with Answers
Free PDF Download of CBSE Class 10 Maths Chapter 4 Quadratic Equations Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Quadratic Equations MCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 4 Quadratic Equations
1. Which of the following is not a quadratic equation
(a) x² + 3x - 5 = 0
(b) x² + x3 + 2 = 0
(c) 3 + x + x² = 0
(d) x² - 9 = 0
Answer/Explanation
Answer: b
Explaination:Reason: Since it has degree 3.
2. The quadratic equation has degree
(a) 0
(b) 1
(c) 2
(d) 3
Answer/Explanation
Answer: c
Explaination:Reason: A quadratic equation has degree 2.
3. The cubic equation has degree
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: c
Explaination:Reason: A cubic equation has degree 3.
4. A bi-quadratic equation has degree
(a) 1
(b) 2
(c) 3
(d) 4
Answer/Explanation
Answer: d
Explaination:Reason: A bi-quadratic equation has degree 4.
5. The polynomial equation x (x + 1) + 8 = (x + 2) {x - 2) is
(a) linear equation
(b) quadratic equation
(c) cubic equation
(d) bi-quadratic equation
Answer/Explanation
Answer: a
Explaination:Reason: We have x(x + 1) + 8 = (x + 2) (x - 2)
⇒ x² + x + 8 = x² - 4
⇒ x² + x + 8- x² + 4 = 0
⇒ x + 12 = 0, which is a linear equation.
6. The equation (x - 2)² + 1 = 2x - 3 is a
(a) linear equation
(b) quadratic equation
(c) cubic equation
(d) bi-quadratic equation
Answer/Explanation
Answer: b
Explaination:Reason: We have (x - 2)² + 1 = 2x - 3
⇒ x² + 4 - 2 × x × 2 + 1 = 2x - 3
⇒ x² - 4x + 5 - 2x + 3 = 0
∴ x² - 6x + 8 = 0, which is a quadratic equation.
9. The quadratic equation whose one rational root is 3 + √2 is
(a) x² - 7x + 5 = 0
(b) x² + 7x + 6 = 0
(c) x² - 7x + 6 = 0
(d) x² - 6x + 7 = 0
Answer/Explanation
Answer: d
Explaination:Reason: ∵ one root is 3 + √2
∴ other root is 3 - √2
∴ Sum of roots = 3 + √2 + 3 - √2 = 6
Product of roots = (3 + √2)(3 - √2) = (3)² - (√2)² = 9 - 2 = 7
∴ Required quadratic equation is x² - 6x + 7 = 0
10. The equation 2x² + kx + 3 = 0 has two equal roots, then the value of k is
(a) ±√6
(b) ± 4
(c) ±3√2
(d) ±2√6
Answer/Explanation
Answer: d
Explaination:Reason: Here a = 2, b = k, c = 3
Since the equation has two equal roots
∴ b² - 4AC = 0
⇒ (k)² - 4 × 2 × 3 = 0
⇒ k² = 24
⇒ k = ± √24
∴ k= ±
= ± 2√6
13. The sum of the roots of the quadratic equation 3×2 - 9x + 5 = 0 is
(a) 3
(b) 6
(c) -3
(d) 2
Answer/Explanation
Answer: c
Explaination:Reason: Here a = 3, b = -9, c = 5
∴ Sum of the roots
17. If a, p are the roots of the equation (x - a) (x - b) + c = 0, then the roots of the equation (x - a) (x - P) = c are
(a) a, b
(b) a, c
(c) b, c
(d) none of these
Answer/Explanation
Answer: a
Explaination:Reason: By given condition, (x - a) (x - b) + c = (x - α) (x - β)
⇒ (x - α) (x - β) - c = (x - a) (x - b)
This shows that roots of (x - α) (x - β) - c are a and b
18. Mohan and Sohan solve an equation. In solving Mohan commits a mistake in constant term and finds the roots 8 and 2. Sohan commits a mistake in the coefficient of x. The correct roots are
(a) 9,1
(b) -9,1
(c) 9, -1
(d) -9, -1
Answer/Explanation
Answer: a
Explaination:Reason: Correct sum = 8 + 2 = 10 from Mohan
Correct product = -9 x -1 = 9 from Sohan
∴ x² - (10)x + 9 = 0
⇒ x² - 10x + 9 = 0
⇒ x² - 9x - x + 9
⇒ x(x - 9) - 1(x - 9) = 0
⇒ (x-9) (x-l) = 0 .
⇒ Correct roots are 9 and 1.
19. If a and p are the roots of the equation 2x² - 3x - 6 = 0. The equation whose roots are
and
is
(a) 6x² - 3x + 2 = 0
(b) 6x² + 3x - 2 = 0
(c) 6x² - 3x - 2 = 0
(d) x² + 3x-2 = 0
Answer/Explanation
Answer: b
Explaination:
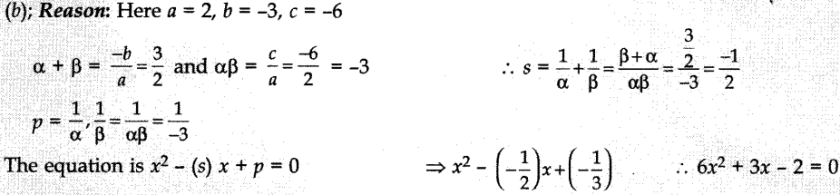
20. If the roots of px2 + qx + 2 = 0 are reciprocal of each other, then
(a) P = 0
(b) p = -2
(c) p = ±2
(d) p = 2
Answer/Explanation
Answer: d
Explaination:Reason: here α =
∴ αβ = 1
⇒
= 1
∴ p = 2
21. If one root of the quadratic equation 2x² + kx - 6 = 0 is 2, the value of k is
(a) 1
(b) -1
(c) 2
(d) -2
Answer/Explanation
Answer: b
Explaination:Reason: Scice x = 2 is a root of the equation 2x² + kx -6 = 0
∴ 2(2)² +k(2) - 6 = 0
⇒ 8 + 2k - 6 = 0
⇒ 2k = -2
∴ k = -1
22. The roots of the quadratic equation
![]()
(a) a, b
(b) -a, b
(c) a, -b
(d) -a, -b
Answer/Explanation
Answer: d
Explaination:
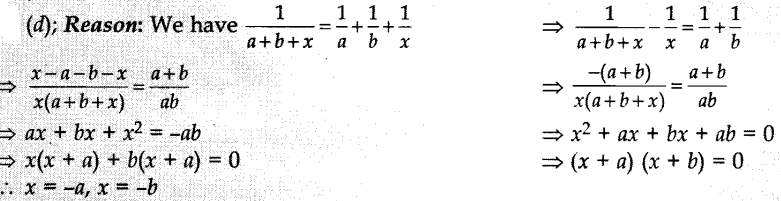
23. The roots of the equation 7x² + x - 1 = 0 are
(a) real and distinct
(b) real and equal
(c) not real
(d) none of these
Answer/Explanation
Answer: a
Explaination:Reason: Here a = 2, b = 1, c = -1
∴ D = b² - 4ac = (1)² - 4 × 2 × (-1) = 1 + 8 = 9 > 0
∴ Roots of the given equation are real and distinct.
24. The equation 12x² + 4kx + 3 = 0 has real and equal roots, if
(a) k = ±3
(b) k = ±9
(c) k = 4
(d) k = ±2
Answer/Explanation
Answer: a
Explaination:Reason: Here a = 12, b = 4k, c = 3
Since the given equation has real and equal roots
∴ b² - 4ac = 0
⇒ (4k)² - 4 × 12 × 3 = 0
⇒ 16k² - 144 = 0
⇒ k² = 9
⇒ k = ±3
25. If -5 is a root of the quadratic equation 2x² + px - 15 = 0, then
(a) p = 3
(b) p = 5
(c) p = 7
(d) p = 1
Answer/Explanation
Answer: c
Explaination:Reason: Since - 5 is a root of the equation 2x² + px -15 = 0
∴ 2(-5)² + p (-5) - 15 = 0
⇒ 50 - 5p -15 = 0
⇒ 5p = 35
⇒ p = 7
26. If the roots of the equations ax² + 2bx + c = 0 and bx² - 2√ac x + b = 0 are simultaneously real, then
(a) b = ac
(b) b2 = ac
(c) a2 = be
(d) c2 = ab
Answer/Explanation
Answer: b
Explaination:Reason: Given equations have real roots, then
D1 ≥ 0 and D2 ≥ 0
(2b)² - 4ac > 0 and (-2√ac)² - 4b.b ≥ 0
4b² - 4ac ≥ 0 and 4ac - 4b2 > 0
b² ≥ ac and ac ≥ b²
⇒ b² = ac
27. The roots of the equation (b - c) x² + (c - a) x + (a - b) = 0 are equal, then
(a) 2a = b + c
(b) 2c = a + b
(c) b = a + c
(d) 2b = a + c
Answer/Explanation
Answer: d
Explaination:Reason: Since roots are equal
∴ D = 0 => b² - 4ac = 0
⇒ (c - a)² -4(b - c) (a - b) = 0
⇒ c² - b² - 2ac -4(ab -b² + bc) = 0 =>c + a-2b = 0 => c + a = 2b
⇒ c² + a² - 2ca - 4ab + 4b² + 4ac - 4bc = 0
⇒ c² + a² + 4b² + 2ca - 4ab - 4bc = 0
⇒ (c + a - 2b)² = 0
⇒ c + a - 2b = 0
⇒ c + a = 2b
28. A chess board contains 64 equal squares and the area of each square is 6.25 cm². A border round the board is 2 cm wide. The length of the side of the chess board is
(a) 8 cm
(b) 12 cm
(c) 24 cm
(d) 36 cm
Answer
Answer: c
29. One year ago, a man was 8 times as old as his son. Now his age is equal to the square of his son's age. Their present ages are
(a) 7 years, 49 years
(b) 5 years, 25 years
(c) 1 years, 50 years
(d) 6 years, 49 years
Answer
Answer: a
30. The sum of the squares of two consecutive natural numbers is 313. The numbers are
(a) 12, 13
(b) 13,14
(c) 11,12
(d) 14,15
Answer
Answer: a
31. Which of the following is not a quadratic equation? [NCERT Exemplar Problems]
(a) 2(x - 1)² = 4x² - 2x + 1
(b) 2x - x² = x² + 5
(c) (√2x + √3 )² + x² = 3x² - 5x
(d) (x² + 2x)² = x4 + 3 + 4x3
Answer/Explanation
Answer: c
Explaination:
2x² + 3 + 2√6 x + x² = 3x² - 5x
2√6x + 5x + 3 = 0
32. If (x - a) is one of the factors of the polynomial ax² + bx + c, then one of the roots of ax² + bx + c = 0 is
(a) 1
(b) c
(c) a
(d) none of these
Answer/Explanation
Answer: c
Explaination:
∵ x - a is one of the factors one root = a.
33. Which of the following are the roots of the quadratic equation, x² - 9x + 20 = 0 by factorisation?
(a) 3, 4
(b) 4, 5
(c) 5, 6
(d) 6, 1
Answer/Explanation
Answer: b
Explaination:
Given equation is x² - 9x + 20 = 0
⇒ x² - 5x - 4x + 20 = 0
⇒ x(x - 5) - 4(x - 5) = 0
⇒ (x - 5) (x - 4) = 0
⇒ either x - 5 = 0 and x - 4 = 0
⇒ x = 5 and x = 4
∴ x = 4 and 5 are the roots/solution of the given quadratic equation.
34. If (1 - p) is a root of the equation x² + px + 1 -p = 0, then roots are
(a) 0, 1
(b) -1, 1
(c) 0, -1
(d) - 1, 2
Answer/Explanation
Answer: c
Explaination:
(1 -p) is a root
∴ (1 - p)² + p(1 - p)+ 1 - p = 0
⇒ (1 - p)[1 - p + p + 1] = 0
⇒ (1 - p)(2) = 0
⇒ p=1
x²+x = 0
One root = 0 and another root = - 1
∴ roots are 0 and - 1.
35. If a, P are roots of the equation x² + 5x + 5 = 0, then equation whose roots are a + 1 and p + 1 is
(a) x² + 5x - 5 = 0
(b) x² + 3x + 5 = 0
(c) x² + 3x + 1 = 0
(d) none of these
Answer/Explanation
Answer: c
Explaination:
α + β = -5, αβ = 5.
Required equation is x² - (α + 1 + β + 1)x + (α + 1) (β + 1) = 0
⇒ x² - (α + β + 2)x + (αβ + α + β +1) = 0
⇒ x² - (-5 + 2)x + (5 - 5 + 1) = 0
⇒ x² + 3x + 1 = 0
36. Which of the following equations has two distinct real roots? [NCERT Exemplar Problems]
(a) 2x² - 3√2x +
=0
(b) x² + x - 5 = 0
(c) x² + 3x + 2√2 = 0
(d) 5x² - 3x + 1 = 0
Answer/Explanation
Answer: b
Explaination: (b) D > 0
37. Which of the following equations has no real roots ? [NCERT Exemplar Problems]
(a) x² - 4x + 3√2 =0
(b) x² + 4x - 3√2 = 0
(c) x² - 4x - 3√2 = 0
(d) 3x² + 4√3x + 4 = 0
Answer/Explanation
Answer: a
Explaination: (a) D < 0
38. (x² + 1)² - x² = 0 has [NCERT Exemplar Problems]
(a) four real roots
(b) two real roots
(c) no real roots
(d) one real root
Answer/Explanation
Answer: c
Explaination: (c) no real roots
39. If the difference of the roots of the equation x² - bx + c = 0 be 1, then
(a) b² - 4c + 1 = 0
(b) b² + 4c = 0
(c) b² - 4c - 1 - 0
(d) b² - 4c = 0
Answer/Explanation
Answer: c
Explaination:
Let roots are α and β
⇒ α - β = 1
∵ (α - β)² = (α + β)² - 4αβ
⇒ 1 = b² - 4c
⇒ b² - 4c - 1 = 0
