MCQ Questions for Class 10 Maths Arithmetic Progressions with Answers
MCQ Questions for Class 10 Maths Arithmetic Progressions with Answers
Free PDF Download of CBSE Class 10 Maths Chapter 5 Arithmetic Progressions Multiple Choice Questions with Answers. MCQ Questions for Class 10 Maths with Answers was Prepared Based on Latest Exam Pattern. Students can solve NCERT Class 10 Maths Arithmetic ProgressionsMCQs with Answers to know their preparation level.
Class 10 Maths MCQs Chapter 5 Arithmetic Progressions
1. The nth term of an A.P. is given by an = 3 + 4n. The common difference is
(a) 7
(b) 3
(c) 4
(d) 1
Answer/Explanation
Answer: c
Explaination:Reason: We have an = 3 + 4n
∴ an+1 = 3 + 4(n + 1) = 7 + 4n
∴ d = an+1 - an
= (7 + 4n) - (3 + 4n)
= 7 - 3
= 4
2. If p, q, r and s are in A.P. then r - q is
(a) s - p
(b) s - q
(c) s - r
(d) none of these
Answer/Explanation
Answer: c
Explaination:Reason: Since p, q, r, s are in A.P.
∴ (q - p) = (r - q) = (s - r) = d (common difference)
3. If the sum of three numbers in an A.P. is 9 and their product is 24, then numbers are
(a) 2, 4, 6
(b) 1, 5, 3
(c) 2, 8, 4
(d) 2, 3, 4
Answer/Explanation
Answer: d
Explaination:Reason: Let three numbers be a - d, a, a + d
∴ a - d +a + a + d = 9
⇒ 3a = 9
⇒ a = 3
Also (a - d) . a . (a + d) = 24
⇒ (3 -d) .3(3 + d) = 24
⇒ 9 - d² = 8
⇒ d² = 9 - 8 = 1
∴ d = ± 1
Hence numbers are 2, 3, 4 or 4, 3, 2
4. The (n - 1)th term of an A.P. is given by 7,12,17, 22,... is
(a) 5n + 2
(b) 5n + 3
(c) 5n - 5
(d) 5n - 3
Answer/Explanation
Answer: d
Explaination:Reason: Here a = 7, d = 12-7 = 5
∴ an-1 = a + [(n - 1) - l]d = 7 + [(n - 1) -1] (5) = 7 + (n - 2)5 = 7 + 5n - 10 = 5M - 3
5. The nth term of an A.P. 5, 2, -1, -4, -7 ... is
(a) 2n + 5
(b) 2n - 5
(c) 8 - 3n
(d) 3n - 8
Answer/Explanation
Answer: c
Explaination:Reason: Here a = 5, d = 2 - 5 = -3
an = a + (n - 1)d = 5 + (n - 1) (-3) = 5 - 3n + 3 = 8 - 3n
6. The 10th term from the end of the A.P. -5, -10, -15,..., -1000 is
(a) -955
(b) -945
(c) -950
(d) -965
Answer/Explanation
Answer: a
Explaination:Reason: Here l = -1000, d = -10 - (-5) = -10 + 5 = - 5
∴ 10th term from the end = l - (n - 1 )d = -1000 - (10 - 1) (-5) = -1000 + 45 = -955
7. Find the sum of 12 terms of an A.P. whose nth term is given by an = 3n + 4
(a) 262
(b) 272
(c) 282
(d) 292
Answer/Explanation
Answer: a
Explaination:Reason: Here an = 3n + 4
∴ a1 = 7, a2 - 10, a3 = 13
∴ a= 7, d = 10 - 7 = 3
∴ S12 =
[2 × 7 + (12 - 1) ×3] = 6[14 + 33] = 6 × 47 = 282
8. The sum of all two digit odd numbers is
(a) 2575
(b) 2475
(c) 2524
(d) 2425
Answer/Explanation
Answer: b
Explaination:Reason: All two digit odd numbers are 11,13,15,... 99, which are in A.P.
Since there are 90 two digit numbers of which 45 numbers are odd and 45 numbers are even
∴ Sum =
[11 + 99] =
× 110 = 45 × 55 = 2475
9. The sum of first n odd natural numbers is
(a) 2n²
(b) 2n + 1
(c) 2n - 1
(d) n²
Answer/Explanation
Answer: d
Explaination:Reason: Required Sum = 1 + 3 + 5 + ... + upto n terms.
Here a = 1, d = 3 - 1 = 2
Sum =
[2 × 1 + (n - 1) × 2] =
[2 + 2n - 2] =
× 2n = n²Reason: All two digit odd numbers are 11,13,15,... 99, which are in A.P.
Since there are 90 two digit numbers of which 45 numbers are odd and 45 numbers are even
∴ Sum =
[11 + 99] =
× 110 = 45 × 55 = 2475
10. If (p + q)th term of an A.P. is m and (p - q)tn term is n, then pth term is

Answer/Explanation
Answer: d
Explaination:Reason: Let a is first term and d is common difference
∴ ap + q = m
ap - q = n
⇒ a + (p + q - 1)d = m = ...(i)
⇒ a + (p - q - 1)d = m = ...(ii)
On adding (i) and (if), we get
2a + (2p - 2)d = m + n
⇒ a + (p -1)d =
...[Dividing by 2
∴ an =
15. nth term of the sequence a, a + d, a + 2d,... is
(a) a + nd
(b) a - (n - 1)d
(c) a + (n - 1)d
(d) n + nd
Answer/Explanation
Answer: a
Explaination:Reason: an = a + (n - 1)d
16. The 10th term from the end of the A.P. 4, 9,14, ..., 254 is
(a) 209
(b) 205
(c) 214
(d) 213
Answer/Explanation
Answer: a
Explaination:Reason: Here l - 254, d = 9-4 = 5
∴ 10th term from the end = l - (10 - 1 )d = 254 -9d = 254 = 9(5) = 254 - 45 = 209
17. If 2x, x + 10, 3x + 2 are in A.P., then x is equal to
(a) 0
(b) 2
(c) 4
(d) 6
Answer/Explanation
Answer: d
Explaination:Reason: Since 2x, x + 10 and 3x + 2 are in A.P.
∴ 2(x + 10) = 2x + (3x + 2)
⇒ 2x + 20 - 5x + 2
⇒ 2x - 5x = 2 - 20
⇒ 3x = 18
⇒ x = 6
18. The sum of all odd integers between 2 and 100 divisible by 3 is
(a) 17
(b) 867
(c) 876
(d) 786
Answer/Explanation
Answer: b
Explaination:Reason: The numbers are 3, 9,15, 21, ..., 99
Here a = 3, d = 6 and an = 99
∴ an = a + (n - 1 )d
⇒ 99 = 3 + (n - 1) x 6
⇒ 99 = 3 + 6n - 6
⇒ 6n = 102
⇒ n = 17
Required Sum =
[a + an] =
[3 + 99] =
× 102 = 867
19. If the numbers a, b, c, d, e form an A.P., then the value of a - 4b + 6c - 4d + e is
(a) 0
(b) 1
(c) -1
(d) 2
Answer/Explanation
Answer: a
Explaination:Reason: Let x be the common difference of the given AP
∴ b = a + x, c = a + 2x, d = a + 3x and e = a + 4x
∴ a - 4b + 6c - 4d + e = a - 4 (a + x) + 6(a + 2x) - 4(a + 3x) + (a + 4x)
= a - 4a - 4x + 6a + 12x - 4a - 12x + a + 4x = 8a - 8a + 16x - 16x = 0
20. If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then 18th term is
(a) 18
(b) 9
(c) 77
(d) 0
Answer/Explanation
Answer: d
Explaination:Reason: We have 7a7 = 11a11
⇒ 7[a + (7 - 1)d] = 11[a + (11 - 1 )d]
⇒ 7(a + 6d) = 11(a + 10d)
⇒ 7a + 42d = 11a + 110d
⇒ 4a = -68d
⇒ a = -17d
∴ a18 = a + (18 - 1)d = a + 17d = -17d + 17d = 0
21. If p, q, r are in AP, then p3 + r3 - 8q3 is equal to
(a) 4pqr
(b) -6pqr
(c) 2pqr
(d) 8pqr
Answer/Explanation
Answer: b
Explaination:
∵ p, q, r are in AP.
∴ 2q = p + r
⇒ p + r - 2q = 0
∴ p3 + r3 + (-2p)3 = 3 × p × r × -2q
[Using ifa + 6 + c = 0 ⇒ a3 + b3 + c3 = 3 abc]
⇒ p3 + r3 - 8q3 = -6pqr.
22. In an AP, if a = 3.5, d = 0, n = 101, then a will be [NCERT Exemplar Problems]
(a) 0
(b) 3.5
(c) 103.5
(d) 104.5
Answer/Explanation
Answer: b
Explaination: (b) a101 = 3.5 + 0(100) = 3.5
23. The list of numbers -10, -6, -2, 2, ... is [NCERT Exemplar Problems]
(а) an AP with d = -16
(b) an AP with d = 4
(c) an AP with d = -4
(d) not an AP
Answer/Explanation
Answer: b
Explaination: (b) An AP with d = 4.
24. Two APs have the same common difference. . The first term of one of these is -1 and that of the other is -8. Then the difference between their 4th terms is [NCERT Exemplar Problems]
(a) -1
(b) -8
(c) 7
(d) -9
Answer/Explanation
Answer: c
Explaination:
a4 - b4 = (a1 + 3d) - (b1 + 3d)
= a1 - b1= - 1 - (-8) = 7
25. In an AP, if d = -2, n = 5 and an = 0, the value of a is
(a) 10
(b) 5
(c) -8
(d) 8
Answer/Explanation
Answer: d
Explaination:
d = - 2, n = 5, an = 0
∵ an = 0
⇒ a + (n - 1)d=0
⇒ a + (5 - 1)(- 2) = 0
⇒ a = 8
Correct option is (d).
26. If the common difference of an AP is 3, then a20 - a15 is
(a) 5
(b) 3
(c) 15
(d) 20
Answer/Explanation
Answer: c
Explaination:
Common difference, d = 3
a20 - a15 = (a + 19d) - (a+ 14d)
= 5d=5 × 3 = 15
27. The next term of the AP √18, √50, √98, ........ is
(a) √146
(b) √128
(c) √162
(d) √200
Answer/Explanation
Answer: c
Explaination:
(c) √18, √50, √98, ..... = 3√2, 5√2, 7√2, ......
∴ Next term is 9√2 = √162
28. The common difference of the AP
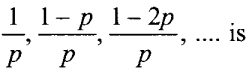
(a) p
(b) -p
(c) -1
(d) 1
Answer/Explanation
Answer: c
Explaination: (c) Common difference = a2 - a1
29. If the nth term of an AP is (2n +1), then the sum of its first three terms is
(a) 6n + 3
(b) 15
(c) 12
(d) 21
Answer/Explanation
Answer: b
Explaination:
a1= 2 × 1 + 1 = 3,
a2 = 2 × 2 + 1 = 5,
a3 = 2 × 3 + l= 7
∴ Sum = 3 + 5 + 7 = 15
30. An AP consists of 31 terms. If its 16th term is m, then sum of all the terms of this AP is
(a) 16 m
(b) 47 m
(c) 31 m
(d) 52 m
Answer/Explanation
Answer: c
Explaination:
S31 =
(2a + 30d)
a16 = a + 15d = zw
⇒ S31 =
× 2(a + 15d)
⇒ S31 = 31m
31. The first term of an AP of consecutive integers is p² + 1. The sum of 2p + 1 terms of this AP is
(a) (p + 1)²
(b) (2p + 1) (p + 1)²
(c) (p+1)3
(d) p3 + (p + 1)3
Answer/Explanation
Answer: d
Explaination:
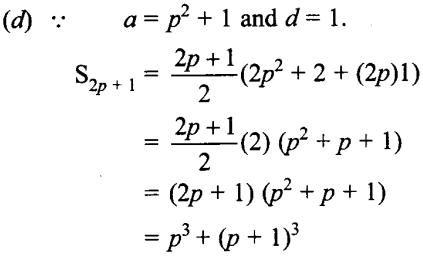
32. If the sum of first n terms of an AP is An + Bn² where A and B are constants, the common difference of AP will be
(a) A + B
(b) A - B
(c) 2A
(d) 2B
Answer/Explanation
Answer: d
Explaination:
Sn = An + Bn²
S1 = A × 1 +B × 1²
= A + B
∵ S1 = a1
∴ a1 = A + B ... (1)
and S2 = A × 2 + B × 2²
⇒ a1 + a2 = 2A + 4B
⇒ (A + B) + a2 = 2A + 4B[Using (i)]
⇒ a2 = A + 3B
∴ d = a2 - a1 = 2B
33. If p - 1, p + 3, 3p - 1 are in AP, then p is equal to ______ .
Answer/Explanation
Answer:
Explaination:
∵ p - 1, p + 3 and 3p - 1 are in AP.
∴ 2(p + 3) = p - 1 + 3p - 1
⇒ 2p + 6 = 4/> -2.
⇒ -2p = -8
⇒ p = 4.
34. Write down the first four terms of the sequences whose general terms are
(i) Tn = 2n + 3
(ii) Tn =3n + 1
(iii) T1 = 2, Tn = Tn-1+ 5, n ≥ 2
Answer/Explanation
Answer:
Explaination:
(i) Tn= 2n + 3
T1 = 2 × 1 + 3 = 5,
T2 = 2 × 2 + 3 = 7,
T3 = 2 × 3 + 3 = 9,
T4 = 2 × 4 + 3 = 11
∴ Ist four terms are 5, 7, 9 and 11.
(ii) Tn = 3n+1
⇒ T1 = 31+1 = 9,
T2 = 32+1 = 27,
T3= 33+1 = 81,
T4 = 34+1 = 243
∴ Ist four terms are 9, 27, 81 and 243
(iii) T1 = 2, Tn = Tn-1 + 5, n ≥ 2
⇒ T2 = T2-1 + 5
= T1 + 5 = 2 + 5 = 7
T3 = T3-1 + 5
= T2 + 5 = 7 + 5 = 12
and T4=T4-1 + 5
= T3 + 5 = 12 + 5 = 17
∴ Ist four terms are 2, 7, 12 and 17.
35. Find:
The 10th term of 10.0, 10.5, 11.0, 11.5, .....
Answer/Explanation
Answer:
Explaination:
a=10, d = 10.5 - 10 = 0.5
a10 = a + 9d= 10 + 9 × 0.5 = 14.5
36. In an A.P., if the common difference (d) = - 4 and the seventh term (a7) is 4, then find the first term. [CBSE 2018]
Answer/Explanation
Answer:
Explaination:
Let a = first term,
Given, d = - 4, a7 = 4
⇒ a + (7 - 1)d = 4
[ ∵ nth term of an AP = an = a + (n - 1)d]
⇒ a + 6d = 4
⇒ a + 6 × (-4) = 4
⇒ a - 24 = 4.
⇒ a = 4 + 24 = 28
∴ First term, a = 28
38. Which term of the AP 21, 18, 15, ... , is zero?
Answer/Explanation
Answer:
Explaination:
Here, a = 21, J= 18-21 = -3
Let an = 0
⇒ a + (n - 1 )d = 0
⇒ 21 +(n - 1)(-3) = 0
⇒ (n - 1)(- 3) = -21
⇒ n - 1 =
⇒ n = 8
∴ 8th term is zero.
39. For what value ofp, are 2p+ 1, 13, 5p - 3 three consecutive terms of an AP?
Answer/Explanation
Answer:
Explaination:
If terms are in AP, then
13 - (2p + 1) = (5p - 3) - 13
⇒ 13 - 2p - 1 = 5p - 3 - 13
⇒ 28 = 7p
⇒ p = 4.
40. What is the common difference of an A.P. in which a21 - a7 = 84? [AI 2017]
Answer/Explanation
Answer:
Explaination:
Let ‘cf be the common difference of the AP whose first term is ‘a’
Now, a21 - a7 = 84
⇒ (a + 20d) - (a + 6d)= 84
⇒ 20d - 6d = 84
⇒ 14d = 84
⇒ d = 6
