NCERT Solutions for Class 9 Maths Chapter 2 Polynomials

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.1 are part of NCERT Solutions for Class 9 Maths . Here we have given NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.1.

• Polynomials
• Introduction
• Polynomials In One Variable
• Zeroes Of A Polynomial
• Remainder Theorem
• Factorisation Of Polynomials
• Algebraic Identities
• Summary

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.1

Ex 2.1 Class 9 Maths Question 1.

Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.
(i) 4x² – 3x + 7
(ii) y² + √2
(iii) 3 √t + t√2
(iv) y+2/y
(v) x¹⁰+ y³+t⁵⁰
Solution:
(i) We have 4x² – 3x + 7 = 4x² – 3x + 7x⁰
It is a polynomial in one variable i.e., x
because each exponent of x is a whole number.

(ii) We have y² + √2 = y² + √2y⁰
It is a polynomial in one variable i.e., y
because each exponent of y is a whole number.

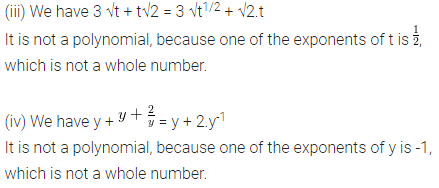
(v) We have x¹⁰+  y³ + t⁵⁰
Here, exponent of every variable is a whole number, but x¹⁰ + y³ + t⁵⁰ is a polynomial in x, y and t, i.e., in three variables.
So, it is not a polynomial in one variable.

Ex 2.1 Class 9 Maths Question 2.
Write the coefficients of x² in each of the following
(i) 2 + x² + x
(ii) 2 – x² + x³
(iii)π/2 x² + x
(iv) v2 x – 1
Solution:
(i) The given polynomial is 2 + x² + x.
The coefficient of x² is 1.
(ii) The given polynomial is 2 – x² + x³.
The coefficient of x² is -1.
(iii) The given polynomial is π/2 x²+ x.
The coefficient of x² is π/2.
(iv) The given polynomial is v2 x – 1.
The coefficient of x² is 0.

Ex 2.1 Class 9 Maths Question 3.
Give one example each of a binomial of degree 35, and of a monomial of degree 100.
Solution:
(i) Abmomial of degree 35 can be 3x³⁵ -4.
(ii) A monomial of degree 100 can be √2y¹⁰⁰.

NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.2

Ex 2.2 Class 9 Maths Question 1.

Find the value of the polynomial 5x – 4x² + 3 at
(i) x = 0
(ii) x = – 1
(iii) x = 2
Solution:
1et p(x) = 5x – 4x² + 3
(i) p(0) = 5(0) – 4(0)² + 3 = 0 – 0 + 3 = 3
Thus, the value of 5x – 4x² + 3 at x = 0 is 3.
(ii) p(-1) = 5(-1) – 4(-1)² + 3
= – 5x – 4x² + 3 = -9 + 3 = -6
Thus, the value of 5x – 4x² + 3 at x = -1 is -6.
(iii) p(2) = 5(2) – 4(2)² + 3 = 10 – 4(4) + 3
= 10 – 16 + 3 = -3
Thus, the value of 5x – 4x² + 3 at x = 2 is – 3.

Ex 2.2 Class 9 Maths Question 2.

Find p (0), p (1) and p (2) for each of the following polynomials.
(i) p(y) = y² – y +1
(ii) p (t) = 2 +1 + 2t² -t³
(iii) P (x) = x³
(iv) p (x) = (x-1) (x+1)
Solution:
(i) Given that p(y) = y² – y + 1.
∴ P(0) = (0)² – 0 + 1 = 0 – 0 + 1 = 1
p(1) = (1)² – 1 + 1 = 1 – 1 + 1 = 1
p(2) = (2)² – 2 + 1 = 4 – 2 + 1 = 3
(ii) Given that p(t) = 2 + t + 2t² – t³
∴p(0) = 2 + 0 + 2(0)² – (0)³
= 2 + 0 + 0 – 0=2
P(1) = 2 + 1 + 2(1)² – (1)³
= 2 + 1 + 2 – 1 = 4
p( 2) = 2 + 2 + 2(2)² – (2)³
= 2 + 2 + 8 – 8 = 4
(iii) Given that p(x) = x³
∴ p(0) = (0)³ = 0, p(1) = (1)³ = 1
p(2) = (2)³ = 8
(iv) Given that p(x) = (x – 1)(x + 1)
∴ p(0) = (0 – 1)(0 + 1) = (-1)(1) = -1
p(1) = (1 – 1)(1 +1) = (0)(2) = 0
P(2) = (2 – 1)(2 + 1) = (1)(3) = 3

NCERT So1utions for C1ass 9 Maths Chapter 2 Polynomials Ex 2.3

Ex 2.3 Class 9 Maths Question 1.

Find the remainder when x³ + 3x² + 3x + 1 is divided by
(i) x + 1
(ii) x – 1/2
(iii) x
(iv) x + π
(v) 5 + 2x
Solution:
Let p(x) = x³ + 3x² + 3x +1
(i) The zero of x + 1 is -1.
∴ p(-1) = (-1)3 + 3(-1)2 + 3(-1) +1
= -1 + 3- 3 + 1 = 0
Thus, the required remainder = 0

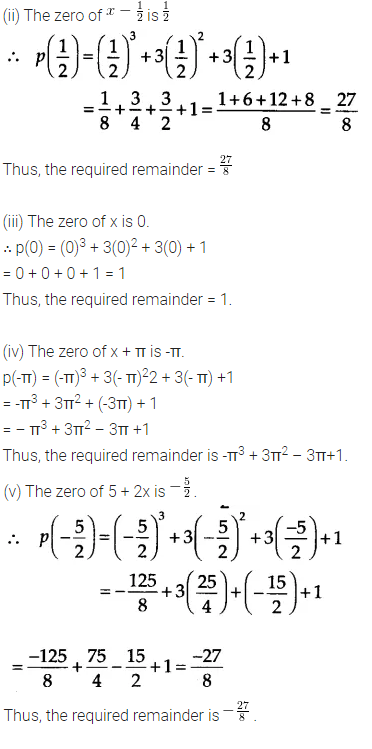
Ex 2.3 Class 9 Maths Question 2.

Find the remainder when x³ – ax² + 6x – a is divided by x – a.
Solution:
We have, p(x) = x³ – ax² + 6x – a and zero of x – a is a.
∴ p(a) = (a)³ – a(a)² + 6(a) – a
= a³ – a³ + 6a – a = 5a
Thus, the required remainder is 5a.

NCERT So1utions for Class 9 Maths Chapter 2 Polynomials Ex 2.4

Ex 2.4 Class 9 Maths Question 1.

Determine which of the following polynomials has (x +1) a factor.
(i) x³+x²+x +1
(ii) x⁴ + x³ + x² + x + 1
(iii) x⁴ + 3x³ + 3x² + x + 1
(iv) x³ – x² – (2 +√2 )x + √2
Solution:
The zero of x + 1 is -1.
(i) Let p (x) = x³ + x² + x + 1
∴ p (-1) = (-1)³ + (-1)² + (-1) + 1 .
= -1 + 1 – 1 + 1
⇒ p (- 1) = 0
  So, (x+ 1) is a factor of x³ + x² + x + 1.

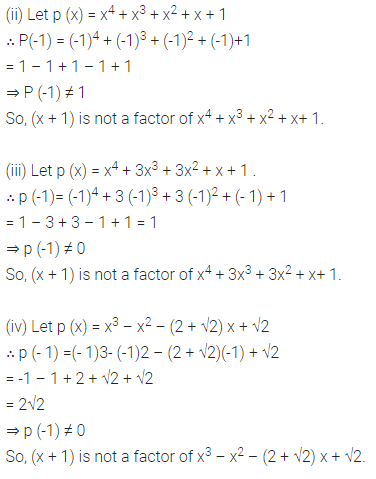
Ex 2.4 Class 9 Maths Question 2.

Use the Factor Theorem to determine whether g (x) is a factor of p (x) in each of the following cases
(i) p (x)= 2x³ + x² – 2x – 1, g (x) = x + 1
(ii) p(x)= x³ + 3x² + 3x + 1, g (x) = x + 2
(iii) p (x) = x³ – 4x² + x + 6, g (x) = x – 3
Solution:
(i) We have, p (x)= 2x³ + x² – 2x – 1 and g (x) = x + 1
∴ p(-1) = 2(-1)³ + (-1)² – 2(-1) – 1
= 2(-1) + 1 + 2 – 1
= -2 + 1 + 2 -1 = 0
⇒ p(-1) = 0, so g(x) is a factor of p(x).

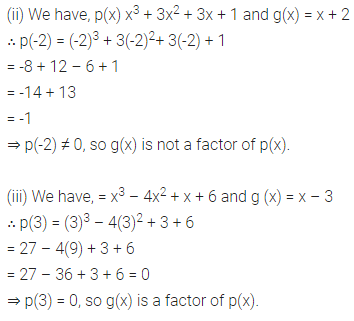
NCERT Solutions for Class 9 Maths Chapter 2 Polynomials Ex 2.5

Ex 2.5 Class 9 Maths Question 1.

Use suitable identities to find the following products
(i) (x + 4)(x + 10)
(ii) (x+8) (x -10)
(iii) (3x + 4) (3x – 5)

Ex 2.5 Class 9 Maths Question 2.

Evaluate the following products without multiplying directly
(i) 103 x 107
(ii) 95 x 96
(iii) 104 x 96
Solution:
(i)We have, 103 x 107 = (100 + 3) (100 + 7)
= ( 100)² + (3 + 7) (100)+ (3 x 7)
[Using (x + a)(x + b) = x² + (a + b)x + ab]
= 10000 + (10) x 100 + 21
= 10000 + 1000 + 21=11021

(ii) We have, 95 x 96 = (100 – 5) (100 – 4)
= ( 100)² + [(- 5) + (- 4)] 100 + (- 5 x – 4)
[Using (x + a)(x + b) = x² + (a + b)x + ab]
= 10000 + (-9) + 20 = 9120
= 10000 + (-900) + 20 = 9120

(iii) We have 104 x 96 = (100 + 4) (100 – 4)
= (100)²-4²
[Using (a + b)(a -b) = a²– b²]
= 10000 – 16 = 9984