TS Inter 1st Year Maths 1A Solutions Chapter 1 Functions Ex 1(c)

TS Inter 1st Year Maths 1A Functions Solutions Exercise 1(c)
I.
Question 1.
Find the domains of the following real valued functions. (May 2014, Mar. 14)
(i) f(x) = 1/(x²−1)(x+3)
Answer:
Domain of f is the value of all real x for which (x² – 1) (x + 3) ≠ 0
⇔ (x + 1) (x – 1) (x + 3) ≠ 0
⇔ x ≠ – 1, 1, -3
∴ Domain of f is, R – {-1, 1, – 3}
(ii) f(x) = 2x²−5x+7/(x−1)(x−2)(x−3)
Answer:
Here (x – 1) (x – 2) (x – 3) + 0
⇔ x ≠ 1, x ≠ 2, x ≠ 3.
Domain of f is, R – {1, 2, 3}
(iii) f(x) = 1/log(2−x)
Answer:
f(x) = 1/log(2−x) ∈ R
⇔ log (2 – x) ≠ 0 and 2 – x > 0
⇔ 2 – x ≠ 1 and 2 > x
⇔ x ≠ 1 and x < 2
⇔ x ∈ (-∞, 1) U (1, 2)
(or) x ∈ (-∞, 2) – {1}
Domain of f = x ∈ {∞, 2} – {1}

(iv) f(x) = |x – 3|
Answer:
f(x) = |x – 3| ∈ R
⇔ x ∈ R
∴ Domain of f = R
(v) f(x) = √4x−x². (May 2005)
Answer:
f(x) = √4x−x² ∈ R
⇔ 4x – x² ≥ 0
⇔ x(4 – x) ≥ 0
⇔ x ∈ [0, 4]
∴ Domain of f = [0, 4]
(vi) f(x) = 1/√1−x²
Answer:
f(x) = 1/√1−x²2 0 ⇔ (1 – x)(1 – x) > 0 ⇔ x ∈ (-1, 1) ∴ Domain of f = {x/x ∈ (-1, 1)} (vii) f(x) = 3^x/x+1
Answer:
f(x) = 3^x/x+1 ∈ R
⇔ 3x ∈ R, ∀ x ∈ R and x + 1 ≠ 0
⇔ x ≠ – 1
∴ Domain of f = R – {-1}
(viii) f(x) = √x²−25 (May 2012)
Answer:
f(x) = √x²−25 ∈ R
⇔ x2 – 25 ≥ 0
⇔ (x + 5)(x – 5) ≥ 0
⇔ x ∈ (-∞, -5] ∪ [5, ∞)
⇔ x ∈ R – (-5, 5)
∴ Domain of f is R – (-5, 5)

(ix) f(x) = √x−[x]
Answer:
f(x) = √x−[x] ∈ R
⇔ x – [x] ≥ 0
⇔ x ≥ [x]
⇔ x ∈ R
∴ Domain of f is R
(x) f(x) = √[x]−x
Answer:
f(x) = √[x]−x ∈ R
⇔ [x] – x ≥ 0
⇔ [x] ≥ x
⇔ x ≤ [x]
⇔ x ∈ z
∴ Domain of f is Z (Set of injection)

Question 2.
Find the ranges of the following real valued functions,
(i) log |4 – x²|

Answer:
Let y = f(x) = log |4 – x²| ∈ R
⇔ 4 – x² ≠ 0 ⇒ x ≠ ± 2
y = log|4 – x²|
⇒ |4 – x²| = e^y
e^y > 0 ∀ y ∈ R
∴ Range of f is R.
(ii) √[x]−x
Answer:
Let y = f(x) = √[x]−x ∈ R
⇔ [x] – x > 0
⇔ [x] ≥ x ⇔ x ≤ [x]
∴ Domain of f is z
Then Range of f is {0}
∴ The Range of f = [1, ∞]
(iii) sinπ[x]/1+[x]²
Answer:
Let y = f(x) = sinπ[x]/1+[x]² ∈ R
⇔ x ∈ R
∴ Domain of f is R
For x ∈ R, [x] is an integer and sin n [x]= 0 ∀ n ∈ R Range of f is {0}
(iv) x²−4/x−2
Answer:
Let y = f(x) = x²−4/x−2 = (x + 2) ⇔ x – 2 ≠ 0
∴ Domain of f is R – {2}
Then y = x + 2 ∴ x ≠ 2, we have y ≠ 4
∴ Range of f is R – {4}.
(v) √9+x²
Answer:
Let y = √9+x² f(x) ∈ R
Domain of f is R.
When x = 0, f (0) = √9 = ± 3, But when f(0) = 3,
For all values of x e R – {0}, f (x) > 3
Range of f = {3, ∞).

Question 3.
If f and g are real valued functions defined by f(x) – 2x – 1 and g(x) = x², then find
(i) (3f – 2g)(x)

Answer:
(3f – 2g) (x) = 3 f(x) – 2 g(x)= 3 (2x – 1) – 2(x²)
= -2x² + 6x – 3

(ii) (fg) (x)
Answer:
(fg)(x) = f(x) g(x) = (2x – 1)(x²) = 2x³ – x²

(iii) (√f/g)(x)
Answer:
√f(x)/g(x)=√2x−1/x²

(iv) (f + g + 2)(x)
Answer:
(f + g + 2) (x) = f(x) + g(x) + 2
= 2x – 1 + x² + 2
= x² + 2x + 1 = (x + 1)²

Question 4.
If f = {(1, 2), (2, -3), (3, -1)}, then find
(i) 2f
(ii) 2 + f
(iii) f²
(iv) √f
[May 2012, May 2008]

Answer:
Given f = {(1, 2), (2, -3), (3, -1)} we have f(1) = 2, f(2) = -3 and f(3) = -1
(i) 2f = {(1, 2 x 2), (2, 2 (-3), (3, 2(-1))}
= {(1. 4). (2, – 6). (3, -2)}
(ii) 2 + f = {(1, 2+2), (2, 2+(-3), (3, 2+(-1))}
= {(1, 4), (2, -1), (3. 1)}

(iii) f² = {(1, 22), (2, (-3)2), (3, (-1)2)]
= {(1, 4), (2, 9), (3, 1)}

(iv) √f = {(1, √2)| (∵ √-3 and √-1 are not real)

II.

Question 1.
Find the domains of the following real valued functions
(i) f(x)= √x²−3x+2

Answer:
f(x) = √x²−3x+2 ∈ R
Domain of f is x² -3x + 2 > 0
⇒ (x – 2) (x – 1) > 0
⇒ x ∈ [-∞, 1] u [2, ∞]
∴ Domain of f = R – [1, 2]

(ii) f (x) = log (x² – 4x + 3)
Answer:
f(x) = log (x² – 4x + 3) ∈ R
⇔ x² – 4x + 3 > 0
⇔ (x – 3) (x – 1) > 0
x ∈ (-∞, 1) ∪ (3, ∞)
Domain f = R – (1, 3)

(iii) f(x) = √2+x+√2−x/x
Answer:
f(x) = √2+x+√2−x/x ∈ R
⇔ 2 + x > 0 2 – x > 0, x ≠ 0
⇔ x > -2, x < 2 x ≠ 0 ⇔ -2 < x < 2, x ≠ 0 Domain of f is [-2, 2] – {0} (iv) f(x) = 1/3√x−2 log (4−x)¹⁰ Answer: f(x) = 1/3√x−2log(4−x)¹⁰ ∈ R ⇔ 4 – x > 0, 4 – x ≠ 1 and x – 2 ≠ 0
⇔ x < 4, x ≠ 3, x ≠ 2 Domain of f is [-∞, 4] – {2, 3} (v) f(x) = √4−x²/[x]+2 Answer: f(x) = √4−x²/[x]+2 ∈ R ⇔ 4 – x > 0, [x] + 2 > 0 or
4 – x² < 0 and [x] > + 2 < 0 When 4 – x² > 0, and [x] + 2 > 0
we have (2 – x) (2 + x) > 0 and [x] > – 2
⇔ x ∈ [-2, 2] and x ∈ [-1, ∞)
⇔ x ∈ [-1, 2] …………….(1)
When 4 – x2 < 0, and [x] + 2 < 0 ⇔ (2 + x) (2 – x) < 0 and [x] + 2 < 0 ⇔ x ∈ [-∞, -2] ∪ [2, ∞] and [x] < – 2 ⇔ x ∈ [- ∞, -2] ∪ [2, ∞] and x ∈ (- ∞,-2) ⇔ x ∈ [-∞, -2] ………………(2) ∴ from (1) and (2) ∴ Domain of f is [-∞, -2] ∪ {-1, 2} (vi) f(x) = √log_0.3(x−x²) Answer: f(x) = √log_0.3(x−x²) ∈ R ⇔ log_0.3 (x – x2) > 0 .
⇒ x – x² < (0.3) 0 ⇒ x – x² < 1 ⇒ -x² + x < 1 ⇒ -x² + x – 1 < 0 ⇒ x² – x + 1 > 0
This is true for all x ∈ R …..(1)
and x – x² > 0
⇒ x² – x < 0
⇒ x (x – 1) < 0
⇒ x ∈ (0, 1) ……….(2)
∴ Domain of f is R n (0, 1) = (0, 1)
∴ Domain of f = (0, 1)
(vii) f(x) = 1/x+|x|
Answer:
f(x) = 1/x+|x| ∈ R
⇔ x + |x| ≠ 0 ⇒ x ∈ (0, ∞)
(∵ |x| = x if x ≥ 0
= -x if x < 0)
∴ Domain of f = (0, ∞)

Question 2.
Prove that the real valued function f(x) = x/e^x−1 + x/2 + 1 is an even function on R – {0} –

Answer:
f (x) ∈ R, ex – 1 ≠ 0
⇒ ex ≠ 1 ⇒ x ≠ 0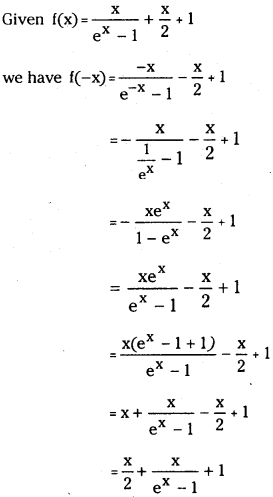

Since f(-x) = f(x), the function f is even function on R – {0}.

Question 3.
Find the domain and range of the following functions.
(i) f(x) = tanπ[x]/1+sinπ[x]+[x²]

Answer:
f(x) = tanπ[x]/1+sinπ[x]+[x²] ∈ R
⇔ x ∈ R; since [x] is an integar so that tan π [x] and sin π [x] are zero. ∀ x ∈ R
Domain of f is R and Range = {0}
(ii) f(x) = x/2−3x
Answer:
f(x) = x/2−3x ∈ R
⇔ 2 – 3x ≠ 0 ⇒ x ≠ 2/3
∴ Domain of f = R – {2/3}
Let y = f(x) = x/2−3x
⇒ 2y – 3xy = x
⇒ 2y = x(1 + 3y)
⇒ x = 2y/1+3y
∴ x ∈ R – {2/3}, 1 + 3y ≠ 0
⇒ y ≠ −1/3
∴ Range of f = R – {−1/3}
(iii) f(x) = |x| + |1 + x|
Answer:
f(x) ∈ R ⇔ x ∈ R
Domain of f = R
∴ |x| = x if x > 0
= – x if x < 0 |1 + x| = 1 + x if 1 + x > 0 ie., x > -1
= – (1 + x) if 1 + x < 0 ie., x < – 1
For x = 0, f(0) = 1,
x= 1, f(1) = |1| + |1 + 1| = 3
x = 2, f(2) = |2| + |1 + 2| = 2 + 3 = 5
x = -2, f(-2) = |-2| + |1 +(-2)| = 2 + 1 = 3
x = -1, f(-1) = |-1| + |1 + (-1)| = 1