TS Inter 1st Year Maths 1A Products of Vectors Solutions Exercise 5(C)

I.
Question 1.
Compute [i̅ – j̅ j̅ – k̅ k̅ – i̅]

Answer:
[i̅ – j̅ j̅ – k̅ k̅ – i̅] = $\left|\begin{array}{rrr} 1 & -1 & 0 \\ 0 & 1 & -1 \\ -1 & 0 & 1 \end{array}\right|$
= 1 (1) + 1 (- 1) = 1 – 1 = 0

Question 2.
If a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then compute a̅ . (b̅ × c̅)

Answer:
Given a̅ = i̅ – 2j̅ – 3k̅, b̅ = 2i̅ + j̅ – k̅, c̅ = i̅ + 3j̅ – 2k̅ then
a̅.(b̅ × c̅) = (a̅ b̅ c̅) = $\left|\begin{array}{ccc} 1 & -2 & -3 \\ 2 & 1 & -1 \\ 1 & 3 & -2 \end{array}\right|$
= 1 (- 2 + 3) + 2 (- 4 + 1) – 3 (6 – 1)
= 1 – 6 – 15 = – 20

Question 3.
If a̅ = (1, -1, -6), b̅ = (1, -3, 4) and c̅ = (2, -5, 3), then compute the following.
(i) a̅ . (b̅ × c̅)

Answer:
a̅ × (b̅ × c̅) = (a̅ . c̅) b̅ – (a̅ . b̅) c̅
= (2 + 5 – 18) b̅ – (1 + 3 – 24) c̅
= -11b̅ + 20c̅
= — 11 (i̅ – 3j̅ + 4k̅) + 20(2i̅ – 5j̅ + 3k̅)
= 29i̅ – 67j̅ + 16k̅

(ii) a̅ × (b̅ × c̅)
Answer:
a̅ × (b̅ × c̅) = (a̅.c̅)b̅ – (a̅.b̅)c̅
= (2 + 5 – 18)b̅ – (1 + 3 – 24)c̅
= -11b̅ + 20c̅
= -11(i̅ – 3j̅ + 4k̅) + 20(2i̅ – 5j̅ + 3k̅)
= 29i̅ – 67j̅ + 16k̅

iii) (a̅ × b̅) × c̅
Answer:
(a̅ × b̅) × c̅
= (a̅ . c̅)b̅ – (b̅ . c̅)a̅
= (2 + 5 – 18) b̅ – (2 + 15 + 12) a̅
= -11 (i̅ – 3j̅ + 4k̅) – 29 (i̅ – j̅ – 6k̅)
= -40i̅ + 62j̅ + 130k̅

Question 4.
Simplify the following :
i) (i̅ – 2j̅ + 3k̅) × (2i̅ + j̅ – k̅) – (j̅ + k̅)

Answer:
(i̅ – 2j̅ + 3k̅) × (2i̅ + j̅ – k̅) – (j̅ + k̅)
= $\left|\begin{array}{rrr} 1 & -2 & 3 \\ 2 & 1 & -1 \\ 0 & 1 & 1 \end{array}\right|$
= 1 (2) + 2(2) + 3(2)
= 2 + 4 + 6
= 12

ii) (2i̅ – 3j̅ + k̅) – (i̅ – j̅ + 2k̅) × (2i̅ + j̅ + k̅)
Answer:
(2 i̅ – 3j̅ + k̅) . (i̅ – j̅ + 2k̅) × (2i̅ + j̅ + k̅)
= $\left|\begin{array}{rrr} 2 & -3 & 1 \\ 1 & -1 & 2 \\ 2 & 1 & 1 \end{array}\right|$
= 2 (- 1 – 2) + 3 (1 – 4) + 1 (1 + 2)
= – 6 – 9 + 3
= -12

Question 5.
Find the volume of the parallelopiped having coterminus edges i̅ + j̅ + k̅, i̅ – j̅ and i̅ + 2j̅ – k̅

Answer:
Let a̅ = i̅ + j̅ + k̅, b̅ = i̅ – j̅ and c̅ = i̅ + 2j̅ – k̅ then the volume of parallelopiped =
| (a̅ b̅ c̅)|
= $\left|\begin{array}{rrr} 1 & 1 & 1 \\ 1 & -1 & 0 \\ 1 & 2 & -1 \end{array}\right|$
= 1 (1) – 1 (- 1) + 1 (2 + 1)
= 1 + 1 + 3 = 5 cubic units.

Question 6.
Find ‘t’ for which the vectors 2i̅ – 3j̅ + k̅, i̅ + 2j̅ – 3k̅ and j̅ – tk̅ are coplanar.

Answer:
Denote the given vectors by a, b, c .and if the vectors are coplanar then [a̅ b̅ c̅] = 0
⇒ $\left|\begin{array}{rrr} 2 & -3 & 1 \\ 1 & 2 & -3 \\ 0 & 1 & -t \end{array}\right|$ = 0
⇒ 2 (- 2t + 3) + 3 (- t) + 1 (1) = 0
⇒ – 7t + 7 = 0
⇒ t = 17.

Question 7.
For non coplanar vectors a̅,b̅ and c̅, determine p for which the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar.

Answer:
Given a,b,c are non coplanar vectors We have [a̅ b̅ c̅] = 0 If the vectors a̅ + b̅ + c̅, a̅ + pb̅ + 2c̅ and -a̅ + b̅ + c̅ are coplanar.
Then $\left|\begin{array}{ccc} 1 & 1 & 1 \\ 1 & p & 2 \\ -1 & 1 & 1 \end{array}\right|$[a̅ b̅ c̅] = 0
⇒ $\left|\begin{array}{rrr} 1 & 1 & 1 \\ 1 & p & 2 \\ -1 & 1 & 1 \end{array}\right|$ = 0 (∵ [a̅ b̅ c̅] = 0)
⇒ 1 (p – 2) – 1 (1 + 2) + 1 (1 + p) = 0
⇒ 2p = 4 ⇒ p = 2

Question 8.
Determine λ for which the volume of the parallelopiped having coterminus edges i̅ + j̅, 3i̅ – j̅ and 3j̅ + λ.k̅ is 16 cubic units.

Answer:
Denoting the coterminus edges by a̅,b̅,c̅ the volume of the parallelopiped =
|[a̅ b̅ c̅]| = ±16
∴ $\left|\begin{array}{rrr} 1 & 1 & 0 \\ 3 & -1 & 0 \\ 0 & 3 & \lambda \end{array}\right|$ = ±16
⇒ 1(-λ) – 1(3λ) = ±16
⇒ – 4λ = ±16
⇒ λ = ±4

Question 9.
Find the volume of the tetrahedron having the edges i̅ + j̅ + k̅; i̅ – j̅ and i̅ + 2j̅ + k̅.

Answer:
Denoting the edges by a̅, b̅, c̅ of tetrahedron, then its volume is = $\frac{1}{6}$[a̅ b̅ c̅]

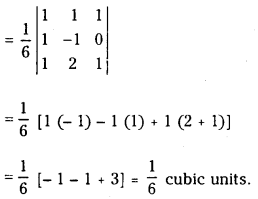
Question 10.
Let a̅, b̅ and c̅ be non coplanar vectors and α = a̅ + 2b̅ + 3c̅, β = 2a̅ + b̅ – 2c̅ and γ = 3a̅ – 7c̅, then find [α̅ β̅ γ̅].

Answer:
Given α = a̅ + 2b̅ + 3c̅
β = 2a̅ + b̅ – 2c̅
γ = 3a̅ – 7c̅
and a̅, b̅, c̅ are non coplanar ⇒ [a̅ b̅ c̅] ≠ 0
then [α̅ β̅ γ̅] = $\left|\begin{array}{rrr} 1 & 2 & 3 \\ 2 & 1 & -2 \\ 3 & 0 & -7 \end{array}\right|$[a̅ b̅ c̅]
= [ 1 (- 7) – 2 (- 14 + 6) + 3 (- 3)] [a̅ b̅ c̅]
= (- 7 + 16 – 9) [a̅ b̅ c̅] = 0

Question 11.
Let a̅, b̅ and c̅ be non coplanar vectors. If [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅] = λ [a̅ b̅ c̅] then find the value of λ.

Answer:
Given a,b,c as non coplanar vectors We have [a̅ b̅ c̅] ≠ 0
∴ $\left|\begin{array}{ccc} 2 & -1 & 3 \\ 1 & 1 & -2 \\ 1 & 1 & -3 \end{array}\right|$[a̅ b̅ c̅]
= [2 (- 3 + 2) + 1 (- 3 + 2) + 3 (1 – 1)][a̅ b̅ c̅]
= [-2 – 1] [a̅ b̅ c̅]
= -3[a̅ b̅ c̅]
Given [2a̅ – b̅ + 3c̅, a̅ + b̅ – 2c̅, a̅ + b̅ – 3c̅]
= λ [a b c]
We have -3[a̅ b̅ c̅] = λ [a̅ b̅ c̅]
⇒ λ = -3

Question 12.
Let a̅, b̅ and c̅ be non coplanar vectors.
If [a̅ + 2b̅ 2b̅ + c̅ 5c̅ + a̅] = λ [a̅ b̅ c̅], then find λ.

Answer:
Given a̅, b̅ and c̅ as non coplanar vectors. We have [a̅ b̅ c̅] ≠ 0. Given that
∴ $\left|\begin{array}{lll} 1 & 2 & 0 \\ 0 & 2 & 1 \\ 1 & 0 & 5 \end{array}\right|$[a̅ b̅ c̅] = λ[a̅ b̅ c̅]
⇒ [1 (10 – 0) – 2 (0 – 1)] [a̅ b̅ c̅] = λ[a̅ b̅ c̅]
⇒ 12 [a̅ b̅ c̅] = λ [a̅ b̅ c̅]
⇒ λ = 12

Question 13.
If a̅, b̅, c̅ are non coplanar vectors, then find the value of $\frac{(\overline{\mathrm{a}}+2 \overline{\mathrm{b}}-\overline{\mathrm{c}}) \cdot[(\overline{\mathrm{a}}-\overline{\mathrm{b}}) \times(\overline{\mathrm{a}}-\overline{\mathrm{b}}-\overline{\mathrm{c}})]}{[\overline{\mathrm{a}} \overline{\mathrm{b}} \overline{\mathrm{c}}]}$

Answer:
Given a̅, b̅, c̅ are non coplanar we have [a̅ b̅ c̅] ≠ 0, then

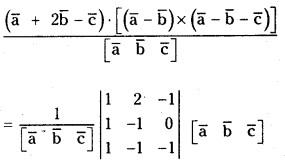
= 1 (1) – 2 (- 1) – 1 (- 1 + 1) = 3

Question 14.
If a̅, b̅, c̅ are mutually perpendicular unit vectors, then find the value of [a̅ b̅ c̅]².

Answer:
Given a̅, b̅, c̅ are mutually perpendicular unit vectors.
We have |a̅| = |b̅| = |c̅| = 1
and taking a̅ = i̅, b̅ = j̅, c̅ = k̅
We have [a̅ b̅ c̅] = [i̅ j̅ k̅]
= i̅ . (j̅ × k̅) = i̅.i̅ = 1
∴ [a̅ b̅ c̅]² = 1

Question 15.
a̅, b̅, c̅ are non zero vectors and a̅ is perpendicular to both b̅ and c̅. If |a̅|= 2, |b̅|= 3, |c̅| = 4 and (b̅, c̅) = $\frac{2 \pi}{3}$ then find |[a̅ b̅ c̅]|. (May 2008)

Answer:
Given a̅, b̅, c̅ are non zero vectors and a is perpendicular to both b̅ and c̅
⇒ a̅ is parallel to (b̅ × c̅)
⇒ (a̅, b̅ × c̅) = 0 (or) 180°
∴ [a̅ b̅ c̅] = [a̅ . b̅ × c̅]

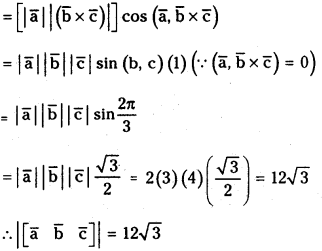
Question 16.
If a̅, b̅, c̅ are unit coplanar vectors, then find [2a̅ – b̅ 2b̅ – c̅ 2c̅ – a̅].

Answer:
Given |a̅| = |b̅| = |c̅| = 1
[2a̅ – b̅ 2b̅ – c̅ 2c̅ – a̅]
= $\left|\begin{array}{rrr} 2 & -1 & 0 \\ 0 & 2 & -1 \\ -1 & 0 & 2 \end{array}\right|$[a̅ b̅ c̅]
= [2 (4) + 1 (- 1)] [a̅ b̅ c̅]
= 7 [a̅ b̅ c̅] = 7 (0) = 0 (∵ a̅, b̅, c̅ are coplanar vectors [a̅ b̅ c̅] = 0 ]

II.
Question 1.
If [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅] = [a̅ b̅ c̅], then show that the points with position vectors a̅, b̅, c̅ and d̅ are coplanar. (May 2014)

Answer:
Given [b̅ c̅ d̅] + [c̅ a̅ d̅] + [a̅ b̅ d̅]
= [a̅ b̅ c̅] ………..(1)
Let OA = a̅, OB = b̅, OC = c̅ and OD = d̅ with respect to a fixed origin ‘O’. Then
AB = b̅ – a̅,
AC = c̅ – a̅,
AD = d̅ – a̅ if the points A, B, C, D are coplanar then
[AB AC AD] = 0
⇒ [b̅ – a̅ c̅ – a̅ d̅ – a̅] = 0
⇒ (b̅ – a̅) . [(c̅ – a̅) × (d̅̅ – a̅)] = 0
⇒ (b̅ – a̅) . [c̅ × d̅ – (c̅ × a̅) – (a̅ × d̅) + (a̅ × a̅)] = 0
⇒ (b̅ – a̅) – [(c̅ × d̅) – (a̅ × d̅) – (c̅ × a̅)] = 0
⇒ [b̅ c̅ d̅] – (b̅ a̅ d̅) – [b̅ c̅ a̅] – [a̅ c̅ d̅] + [a̅ a̅ d̅] + [a̅ c̅ a̅] = 0
⇒ [b̅ c̅ d̅] – [b̅ a̅ d̅] – [b̅ c̅ a̅] – [a̅ c̅ d̅] = 0
⇒ [b̅ c̅ d̅] + [a̅ b̅ a̅] – [a̅ b̅ c̅] + [c̅ a̅ d̅] = 0
⇒ [b̅ c̅ d̅] + [a̅ b̅ d̅] + [c̅ a̅ d̅] = [a̅ b̅ c̅]

Question 2.
If a̅, b̅ and c̅ are non coplanar vectors, then prove that the four points with position vectors 2a̅ + 3b̅ – c̅, a̅ – 2b̅ + 3c̅, 3a̅ + 4b̅ – 2c̅ and a̅ – 6b̅ + 6c̅ are coplanar.

Answer:
Suppose A, B, C, D are the given points with respect to a fixed origin ‘O’ and given that
$\overline{\mathrm{OA}}$ = 2a̅ + 3b̅ – c̅, $\overline{\mathrm{OB}}$ = a̅ – 2b̅ + 3c̅
$\overline{\mathrm{OC}}$ = 3a̅ + 4b̅ – 2c̅ and $\overline{\mathrm{OD}}$ = a̅ – 6b̅ + 6c̅
∴ $\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}$
= (a̅ – 2b̅ + 3c̅) – (2a̅ + 3b̅ – c̅)
= -a̅ – 5b̅ + 4c̅

$\overline{\mathrm{AC}}=\overline{\mathrm{OC}}-\overline{\mathrm{OA}}$
= (3a̅ + 4b̅ – 2c̅) – (2a̅ + 3b̅ – c̅)
= a̅ + b̅ – c̅

$\overline{\mathrm{AD}}=\overline{\mathrm{OD}}-\overline{\mathrm{OA}}$
= (a̅ – 6b̅ + 6c̅) – (2a̅ + 3b̅ – c̅)
= -a̅ – 9b̅ + 7c̅

∴ $\left[\begin{array}{lll} \overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}} \end{array}\right]=\left|\begin{array}{rrr} -1 & -5 & 4 \\ 1 & 1 & -1 \\ -1 & -9 & 7 \end{array}\right|\left[\begin{array}{lll} \overline{\mathbf{a}} & \overline{\mathrm{b}} & \overline{\mathrm{c}} \end{array}\right]$
= [ – 1 (7 – 9) + 5 (7 – 1) + 4 (- 9 + 1)] [a̅ b̅ c̅]
= [- 1 (- 2) + 5 (6) + 4 (- 8)] [a̅ b̅ c̅]
= (2 + 30 – 32) [a̅ b̅ c̅] = 0
Hence the given points A, B, C, D are coplanar.

Question 3.
a̅, b̅ and c̅ are non zero and non collinear vectors and θ ≠ 0, is the angle between b̅ and c̅. If (a̅ × b̅) × c̅ = $\frac{1}{3}$|b̅||c̅||a̅| find sin θ.

Answer:
Given |a̅| ≠ 0, |b̅| ≠ 0, |c̅| ≠ 0 and (b̅, c̅) = θ
and (a̅ × b̅) × c̅ = $\frac{1}{3}$|b̅||c̅|a̅
⇒ (a̅ . c̅) b̅ – (b̅ . c̅) a̅ = $\frac{1}{3}$|b̅||c̅|a̅
∵ a,b, c are non collinear vectors

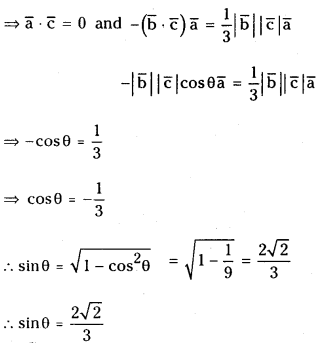
Question 4.
Find the volume of the tatrahedron whose vertices are (1, 2, 1), (3, 2, 5), (2. – 1, 0) and (- 1, 0, 1). (Mar. 2015-T.S) [May 2007]

Answer:
Let O be the origin with A, B, C, D as vertices of tetrahedron.

Question 5.
Show that (a̅ + b̅) . (b̅ + c̅) × (c̅ + a̅) = 2 [a̅ b̅ c̅]

Answer:
(a̅ + b̅) .(b̅ + c̅) × (c̅ + a̅)
= $\left|\begin{array}{lll} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{array}\right|$[a̅ b̅ c̅]
= [1(1) – 1(-1)][a̅ b̅ c̅] = 2[a̅ b̅ c̅]

Question 6.
Show that the equation of the plane passing through the points with position vectors 3i̅ – 5j̅ – k̅, -i̅ + 5j̅ + k̅ and parallel to the vector 3i̅ – j̅ + 7k̅ is 3x + 2y – z = 0.

Answer:
Let $\overline{\mathrm{OA}}$ = (3i̅ – 5 j̅ – k̅), $\overline{\mathrm{OB}}$ = – i̅ + 5j̅ + 7k̅
The given plane passes through the points A, B and parallel to the vector
$\overline{\mathrm{OC}}$ = 3i̅ – j̅ + 7k̅,
$\overline{\mathrm{AB}}=\overline{\mathrm{OB}}-\overline{\mathrm{OA}}$ = -4i̅ + 10j̅ + 8k̅
∴ Equation of the plane is

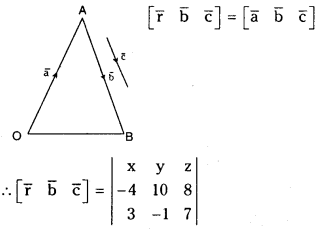
= x (70 + 8) – y (- 28 – 24) + z (4 – 30)
= 78x + 52y – 26z
= 26 (3x + 2y – z)

$\left[\begin{array}{lll} \bar{a} & \bar{b} & \bar{c} \end{array}\right]=\left|\begin{array}{rrr} 3 & -5 & -1 \\ -4 & 10 & 8 \\ 3 & -1 & 7 \end{array}\right|$
= 3 (70 + 8) + 5 (- 28 – 24) – 1 (4 – 30)
= 234 – 260 + 26 = 0
Equation of the required plane is
26 (3x + 2y – z) = 0
⇒ 3x + 2y – z = 0

Question 7.
Prove that a̅ × [a̅ × (a̅ × -(a̅ . a̅) (b̅ × a̅)

Answer:
L.H.S = a × [a̅ × (a̅ × b̅)]
= a̅ × [(a̅ . b̅)a – (a̅. a̅)b̅]
= (a̅. b̅) (a̅ × a̅) – (a̅. a̅) (a̅ × b̅)
= (a̅. b̅) (0) – (a̅. a̅) (a̅ × b̅)
= (a̅. a̅) (b̅ × a̅)
= R.H.S.

Question 8.
If a̅, b̅, c̅ and d̅ are coplanar vectors, then show that (a̅ × b̅) × (c̅ × d̅) = 0.

Answer:
Given a̅, b̅, c̅, d̅ are coplanar vectors
⇒ a̅ × b̅ is perpendicular to the plane S.
In the similar way c̅ × d̅ is perpendicular to the plane S.
a̅ × b̅ and c̅ × d̅
are parallel vectors.
⇒ (a̅ × b̅) × (c̅ × d̅) = 0 (or)
(a̅ × b̅) × (c̅ × d̅) = [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅
= 0b̅ – 0a̅ = 0 (∵ a̅, b̅, c̅, d̅ are coplanar)

Question 9.
Show that [(a̅ × b̅) × (a̅ × c̅)] d̅ = (a̅ . d̅) [a̅ b̅ c̅]

Answer:
We have (a̅ × b̅) × (c̅ × d̅)
= [a̅ c̅ d̅]b̅ – [b̅ c̅ d̅]a̅
(a̅ × b̅) × (a̅ × c̅) = [a̅ a̅ c̅] b̅ – [b̅ a̅ c̅]a̅
= 0(b̅) – [b̅ a̅ c̅] a̅ = (a̅ b̅ c̅)a̅
[(a̅ × b̅) × (a̅ × c̅)] d̅ = [a̅ b̅ c̅](a̅.d̅)

Question 10.
Show that a̅.[(b̅ + c̅) × [a̅ + b̅ + c̅]] = 0

Answer:

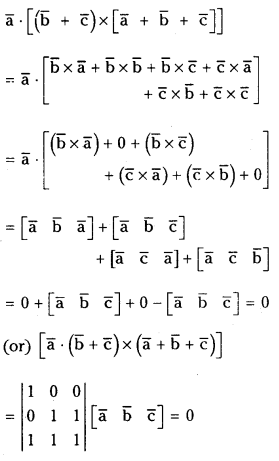
Question 11.
Find λ in order that the four points A (3, 2, 1), B (4, λ, 5), C (4, 2, – 2) and D (6, 5, – 1) are coplanar.

Answer:

⇒ 1(9) – (λ – 2) (- 2 + 9) + 4 (3) = 0
⇒ 21 – (λ – 2)(7) = 0
⇒ λ – 2 = 3
⇒ λ = 5

Question 12.
Find the vector equation of the plane passing through the intersection of planes.
r̅ -(2i̅ + 2j̅ – 3k̅) = 7, r̅ = (2i̅ + 5j̅ + 3k̅) = 9 and through the point (2, 1, 3).

Answer:
The planes are of the form
r̅.n̅₁ = d₁ and r̅.n̅₂ = d₂
The vector equation of the plane passing through the intersection of above plane is of the form
r̅ . (n̅₁ + λn̅₂) = d₁ + λd₂
∴ r̅ . [(2i̅ + 2j̅ – 3k̅) + λ(2i̅ + 5j̅ + 3k̅)]
= 7 + 9λ

Denote r̅ = xi̅ + yj̅ + zk̅ ………..(1)
then (2x + 2y – 3z) + λ (2x + 5y + 3z)] = 7 + 9λ
⇒ (2x + 2y – 3z – 7) + λ (2x + 5y + 3z – 9) = 0 …..(2)
Since this plane passes through the point (2, 1, 3)
We have
(4 + 2 – 9 – 7) + λ (4 + 5 + 9 – 9) = 0
⇒ – 10 + 9λ = 0
⇒ λ = $\frac{10}{9}$
From (2), (2 + 2λ) x + (2 + 5λ) y + (3λ – 3) z – (7 + 9λ) = 0

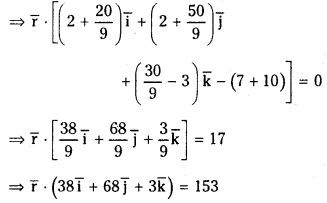
Question 13.
Find the equation of the plane passing through (a̅, b̅, c̅) and parallel to the plane r̅. (i̅ + j̅ + k̅) = 2.

Answer:
Given equation of the plane is
r̅ . (i̅ + j̅ + k̅) = 2
Suppose r̅ = xi̅ + yj̅ + zk̅ then
(xi̅ + yj̅ + zk̅) . (i̅ + j̅ + k̅) = 2
⇒ x + y + z = 2
Equation of parallel plane is x + y + z = k
Since this passes through (a, b, c) we have a + b + c = k
Equation of the required plane is x + y + z = a + b + c

Question 14.
Find the shortest distance between the lines r̅ = 6i̅ + 2j̅ + 2k̅ + λ(i̅ – 2j̅ + 2k̅) and r̅ = -4i̅ – k̅ + μ(3i̅ – 2j̅ – 2k̅).

Answer:
Given lines are

Shortest distance between the lines = 9 units.

Question 15.
Find the equation of the plane passing through the line of intersection of the planes
r̅.(i̅ + j̅ + k̅) = l and r̅.(2i̅ + 3j̅ – k̅) + 4 = 0 and parallel to X – axis.

Answer:
Cartesian form of the given plane is x + y + z = 1 and 2x + 3y – z + 4 = 0
Equation of required plane will be of the form
(x + y + z – 1) + λ (2x + 3y – z + 4) = 0 …………(i)
⇒ (1 + 2λ)x + (1 + 3λ)y + (1 – λ)z – (1 – 4λ) = 0
Since this is parallel to X-axis coefficient of x = 0
⇒ 1 + 2λ = 0 ⇒ λ = $\frac{1}{2}$
Required plane equation from (1) is
(x + y + z – 1) –$\frac{1}{2}$(2x + 3y – z + 4) = 0
⇒ 2x + 2y + 2z – 2 – 2x – 3y + z – 4 = 0
⇒ y – 3z + 6 = 0

Question 16.
Prove that the four points 4i̅ + 5j̅ + k̅, -(j̅ + k̅), 3i̅ + 9j̅ + 4k̅ and -4i̅ + 4j̅ + 4k̅ are coplanar.

Answer:

= – 4 (12 + 3) + 6 (- 3 + 24) – 2(1 + 32)
= -60 + 126 – 66 = 126 – 126 = 0
Given points are coplanar.

Question 17.
If a̅, b̅, c̅ are non coplanar, then show that the vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.

Answer:
Given that a̅, b̅, c̅ are non coplanar
we have [a̅ b̅ c̅] ^O
∴ [a̅ – b̅ b̅ + c̅ c̅ + a̅]
= $\left|\begin{array}{ccc} 1 & -1 & 0 \\ 0 & 1 & 1 \\ 1 & 0 & 1 \end{array}\right|$[a̅ b̅ c̅]
= [1 + 1 (-1)][a̅ b̅ c̅]
= 0 [a̅ b̅ c̅] = 0
∴ Vectors a̅ – b̅, b̅ + c̅, c̅ + a̅ are coplanar.

Question 18.
If a̅, b̅, c̅ are the position vectors of the points A, B and C respectively, then prove that the vector a̅ × b̅ + b̅ × c̅ + c̅ × a̅ is perpendicular to the plane of ΔABC.

Answer:
Let O be the origin and

= (b̅ × c̅) – (b̅ × a̅) – (a̅ × c̅) + (a̅ × a̅)
= (b̅ × c̅) + (a̅ × b̅) + (c̅ × a̅) (∵ (a̅ × a̅) = 0)
= (a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅)
Hence (a̅ × b̅) + (b̅ × c̅) + (c̅ × a̅) is perpendicular to the plane of ΔABC.