I.
Question 1.
If |p̅| = 2, |q̅| = 3 and (p, q) = π/6 , then find |p̅ × q̅|².

Answer:
p̅ × q̅ = |p̅| |q̅| sinθn̂
Given p̅ = 2, q̅ = 3 and (p̅. q̅) = π/6
|p̅ × q̅| = (2) (3)sin π/6 =3
∴ |p̅ × q̅|² = 9

Question 2.
If a̅ = 2i̅ – j̅ + k̅ and b̅ = i̅ – 3j̅ – 5k̅, then find |a̅ × b̅|. (March 2013)

Answer:
a̅ = 2 i̅ – j̅ + k̅ and b̅ = i̅ – 3 j̅ – 5k̅

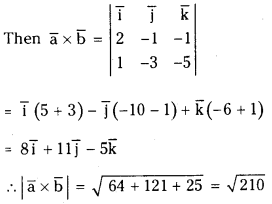
Question 3.
If a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅, then find (a̅ + b̅) × (a̅ – b̅).

Answer:
Given a̅ = 2i̅ – 3j̅ + k̅ and b̅ = i̅ + 4j̅ – 2k̅
Then a̅ + b̅ = 3 i̅ + j̅ – k̅ and a̅ – b̅ = i̅ – 7j̅ + 3k̅
(a + b) × (a – b) = $\left|\begin{array}{rrr} \overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\ 3 & 1 & -1 \\ 1 & -7 & 3 \end{array}\right|$
= i̅(3 – 7) – j̅(9 + l) + k̅ (- 21 – 1)
= -4i̅ – 10j̅ – 22k̅
= -2 (2i̅ + 5j̅ + 11k̅)

Question 4.
If 4i̅ + $\frac{2 p}{3}$ j̅ + pk̅ is parallel to the vector 3 i̅ + 2j̅ + 3k̅, find p.

Answer:
Given 4i̅ + $\frac{2 p}{3}$ j̅ + pk̅ is parallel to
i̅ + 2j̅ + 3k̅
∴ $\frac{4}{1}=\frac{\frac{2 p}{3}}{2}=\frac{p}{3}$
⇒ $\frac{2 p}{3}$ = -4 ⇒ p = 12

Question 5.
Compute
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)

Sol.
a̅ × (b̅ + c̅) + b̅ × (c̅ + a̅) + c̅ × (a̅ + b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) + (b̅ × a̅) + (c̅ × a̅) + (c̅ × b̅)
= (a̅ × b̅) + (a̅ × c̅) + (b̅ × c̅) – (a̅ × b̅) – (a̅ × c̅) – (b̅ × c̅)
= 0

Question 6.
If p̅ = xi̅ + yj̅ + zk̅, then find |p̅ × k̅|².

Answer:
p̅ × k̅ = (xi̅ + yj̅ + zk̅) × k̅
= x(i̅ × k̅) + y(j̅ × k̅) + z(k̅ × k̅)
= -xj̅ + yi̅ + z(0)
= yi̅ – xj̅
|p̅ × k̅|² = x² + y²

Question 7.
Compute 2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅

Sol.
2j̅ × (3i̅ – 4k̅) + (i̅ + 2j̅) × k̅
= 6(j̅ × i̅) – 8(j̅ × k̅) + (i̅ × k̅) + 2(j̅ × k̅)
= -6k̅ – 8i̅ – j̅ + 2i̅
= -6i̅ – j̅ – 6k̅

Question 8.
Find unit vector perpendicular to both i̅ + j̅ + k̅ and 2i̅ + j̅ + 3k̅.

Answer:
Given a̅ = i̅ + j̅ + k̅ and b̅ = 2i̅ + j̅ + 3k̅
then a̅ × b̅ = $\left|\begin{array}{lll} \overline{\mathrm{i}} & \overline{\mathrm{j}} & \overline{\mathrm{k}} \\ 1 & 1 & 1 \\ 2 & 1 & 3 \end{array}\right|$
= i̅(3 – 1) – j̅(3 – 2) + k̅(1 – 2)
= 2i̅ – j̅ – k̅
|a̅ × b̅| = $\sqrt{4+1+1}=\sqrt{6}$
Unit vector perpendicular to both a̅ and b̅
= ±$\frac{\overline{\mathrm{a}} \times \overline{\mathrm{b}}}{|\overline{\mathrm{a}} \times \overline{\mathrm{b}}|}=\pm\left(\frac{2 \overline{\mathrm{i}}-\overline{\mathrm{j}}-\overline{\mathrm{k}}}{\sqrt{6}}\right)$

Question 9.
If θ is the angle between the vectors i̅ + j̅ and j̅ + k̅, then find sin θ.

Answer:
Let a̅ = i̅ + j̅ and b̅ = j̅ + k̅

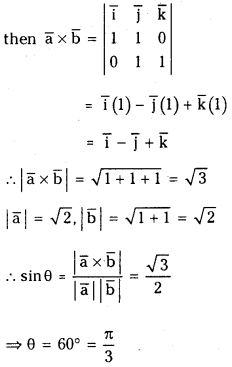
Question 10.
Find the area of the parallelogram having a̅ = 2j̅ – k̅ and b̅ = – i̅ + k̅ as adjacent sides.

Answer:
Vector area of the parallelogram having
a̅ = 2j̅ – k̅ and b̅ = -i̅ + k̅ as adjacent sides = a̅ × b̅
= $\left|\begin{array}{rrr} \bar{i} & \bar{j} & \bar{k} \\ 0 & 2 & -1 \\ -1 & 0 & 1 \end{array}\right|$ = 2 i̅ + j̅ + 2k̅
Area of the parallelogram
= |a̅ × b̅| = $\sqrt{4+1+4}$ = 3 sq. units.

Question 11.
Find the area of the parallelogram whose diagonals are 3i̅ + j̅ – 2k̅ and i̅ – 3j̅ + 4k̅.