Contents
- 1 I. Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions, Question 1. x + y + z = 4 2x + 5y – 2z = 3 x + 7y – 7z = 5 Answer: Augmented matrix of the above system is Rank of the matrix ρ(A) = 2 and ρ(AB) = 3. Since ρ(A) ≠ ρ(AB), the given system of equa¬tions are inconsistent. Question 2. x + y + z = 6 x – y + z = 2 2x – y + 3z = 9
- 2 Question 3. x + y + z = 1 2x + y + z = 2 x + 2y + 2z = 1 (March 2015-T.S)
- 3 Question 5. x + y + z = 6 x + 2y + 3z = 10 x + 2y + 4z = 1
- 4 Question 6. x – 3y – 8z = – 10 3x + y – 4z = 0 2x + 5y + 6z = 13
- 5 Question 7. 2x + 3y + z = 9 x + 2y + 3z = 6 3x + y + 2z = 8
- 6 Question 8. x + y + 4z = 6 3x + 2y – 2z = 9 5x + y + 2z = 13
I.
Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions,
Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Answer:
Augmented matrix of the above system is

Rank of the matrix ρ(A) = 2 and ρ(AB) = 3.
Since ρ(A) ≠ ρ(AB), the given system of equa¬tions are inconsistent.
📚 Top Question Papers & Study Materials
Get latest updates, guess papers and exam alerts instantly.
3,50,000+ Students Already Joined
Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Answer:
Augmented matrix [AB] = ⎡⎣⎢1121−1−1113629⎤⎦⎥
Apply operations R2 – R1, R3 – 2R1, we get

Here ρ(A) = 3 and ρ(AB) = 3
Since ρ(A) = ρ(AB), the given system is consistent and has a unique solution.

Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1 (March 2015-T.S)
Answer:
Augmented matrix of the system is

ρ(AB) = 2 and ρ(A) = 2 and ρ(A) = ρ(AB) < 3
The given system of equations is consis¬tent and has infinitely many solutions.
The given system is equivalent to x + y + z = 1 and y + z = 0.
Solution set is

Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Answer:
Augmented matrix of the system

Here ρ(A) = ρ(AB) = 3; and the system of given equations is consistent; and has a unique solution.
Also x = 1, y = 3, z = 5 form the solution.
Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Answer:
Augmented matrix of the system is

Question 6.
x – 3y – 8z = – 10
3x + y – 4z = 0
2x + 5y + 6z = 13
Answer:
The augmented matrix of the above system is

Since ρ(A) = 2 = ρ(AB) < 3, given system of equations is consistent with infinitely many solutions.
The given system is equivalent to
x – 3y – 8z = – 10,
y + 2z = 3
Put z = t then y = 3 – 2t
∴ x = – 10 + 3(3 – 2t) + 8t
= -10 + 9 – 6t + 8t
= 2t – 1
Hence the solutions are given by
x = 2t – 1, y = 3 – 2t and z = t
Where t is any scalar.
Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Answer:
Augmented matrix of the above system is

ρ(A) = ρ(AB) = 3; system is consistent and has a unique solution given by
x = 3518 , y = 2918 , z = 518
Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Answer:
Augmented matrix of the system

ρ(A) = ρ(AB) = 3;
Hence the system is consistent and has a unique solution given by
x = 2, y = 2, z = 12 .
Augmented matrix of the above system is
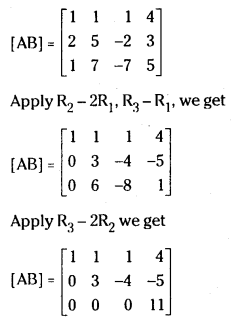
Rank of the matrix ρ(A) = 2 and ρ(AB) = 3.
Since ρ(A) ≠ ρ(AB), the given system of equa¬tions are inconsistent.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Augmented matrix [AB] =
Apply operations R2 – R1, R3 – 2R1, we get

Here ρ(A) = 3 and ρ(AB) = 3
Since ρ(A) = ρ(AB), the given system is consistent and has a unique solution.

x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1 (March 2015-T.S)
Augmented matrix of the system is

ρ(AB) = 2 and ρ(A) = 2 and ρ(A) = ρ(AB) < 3
The given system of equations is consis¬tent and has infinitely many solutions.
The given system is equivalent to x + y + z = 1 and y + z = 0.
Solution set is
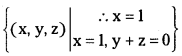
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Augmented matrix of the system

Here ρ(A) = ρ(AB) = 3; and the system of given equations is consistent; and has a unique solution.
Also x = 1, y = 3, z = 5 form the solution.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Augmented matrix of the system is

x – 3y – 8z = – 10
3x + y – 4z = 0
2x + 5y + 6z = 13
The augmented matrix of the above system is

Since ρ(A) = 2 = ρ(AB) < 3, given system of equations is consistent with infinitely many solutions.
The given system is equivalent to
x – 3y – 8z = – 10,
y + 2z = 3
Put z = t then y = 3 – 2t
∴ x = – 10 + 3(3 – 2t) + 8t
= -10 + 9 – 6t + 8t
= 2t – 1
Hence the solutions are given by
x = 2t – 1, y = 3 – 2t and z = t
Where t is any scalar.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Augmented matrix of the above system is
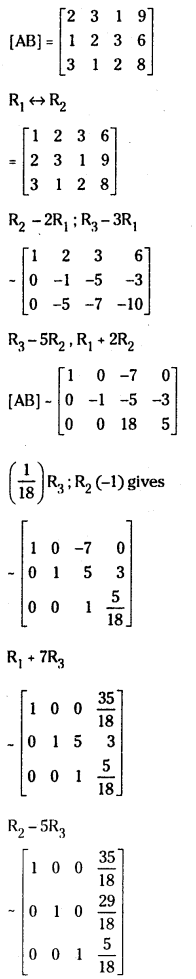
ρ(A) = ρ(AB) = 3; system is consistent and has a unique solution given by
x =
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Augmented matrix of the system
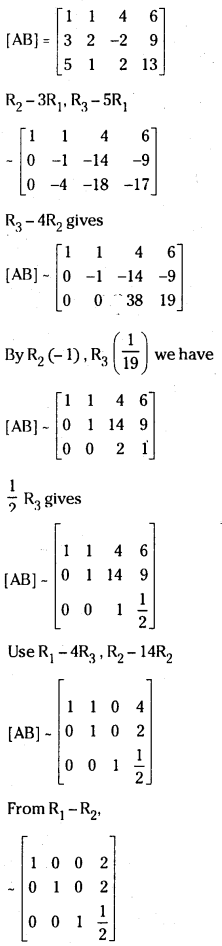
ρ(A) = ρ(AB) = 3;
Hence the system is consistent and has a unique solution given by
x = 2, y = 2, z =



