TS Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(b)

I.
Question 1.
Find the vector equation of the line passing through the point 2i̅ + 3j̅ + k̅ and parallel to the vector 4i̅ – 2j̅ + 3k̅.(March 2015-A.P) (May, March ’01) (V.S.A)

Answer:
Let a = 2i̅ + 3j̅ + k̅ and b = 4i̅ – 2 j̅ + 3k̅
The vector equation of the line passing through the point a̅ and parallel to the vector b̅ is
r̅ = a̅ + tb̅ where t is a scalar.
r̅ = (2i̅ + 3j̅ + k̅) + t (4i̅ – 2j̅ + 3k̅)
⇒ r̅ = (2 + 4t) i̅ + (3 – 2t) j̅ + (1 + 3t) k̅

Question 2.
OABC is a parallelogram. If $\overline{\mathrm{OA}}=\overline{\mathrm{a}}$ and $\overline{\mathrm{OC}}=\overline{\mathrm{c}}$. Find the vector equation of the side BC. (March 2015-T.S) (V.S.A)

Answer:
OABC is a parallelogram.

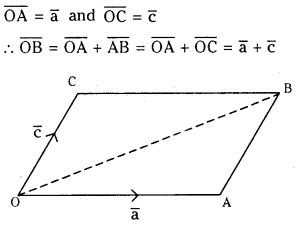
∴ The vector equation of side BC is r̅ = (1 – t)c̅ + t(a̅ + c̅)
= (1 – t + t)c̅ + ta̅
= c̅ + t a̅ where t ∈ R.

Question 3.
If a̅, b̅, c̅ are the position vectors of the vertices A, B and C respectively of a ΔABC, then find the vector equation of the median through the vertex A. (March 2013) (V.S.A)

Answer:

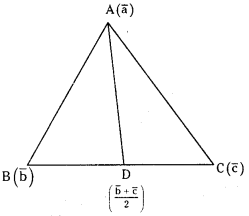
Let $\overline{\mathrm{OA}}=\overline{\mathrm{a}}, \overline{\mathrm{OB}}=\overline{\mathrm{b}}$, and $\overline{\mathrm{OC}}=\overline{\mathrm{c}}$
Vector equation of the median AD is (1 – t)
a̅ + tb̅ = r̅
r̅ = (1 – t)a̅ + t$\left(\frac{\overline{\mathrm{b}}+\overline{\mathrm{c}}}{2}\right)$

Question 4.
Find the vector equation of the line joining the points 2i̅ + j̅ + 3k̅ and – 4i̅ + 3j̅ – k̅.(V.S.A)

Answer:
Let a = 2i̅ + j̅ + 3k̅ and b = -4i̅ + 3 j̅ – k̅
The vector equation of the line passing through the points a,b is
r̅ = (1 – t)a̅ + tb̅, t ∈ R
= a̅ + t (b̅ – a̅)
= (2i̅ + j̅ + 3k̅) + t (-4i̅ + 3j̅ – k̅ – 2i̅ – j̅ – 3k̅)
= (2i̅ + j̅ + 3k̅) +t(-6i̅ + 2j̅ – 4k̅)

Question 5.
Find the vector equation of the plane passing through the points i̅ – 2j̅ + 5k̅, – 5j̅ – k̅ and -3 i̅ + 5j̅. (V.S.A)

Answer:
Let a̅ = i̅ – 2 j̅ + 5k̅, b̅ = -5 j̅ – k̅, c = -3i̅ + 5j̅. (May 2014)
The vector equation of the plane passing through the points a̅, b̅, c̅ is r = (1 – s – t)a̅ + sb̅ + tc̅ where s, t ∈ R
= a̅ + s(b̅ – a̅) + t(c̅ – a̅)
= (i̅ – 2j̅ + 5k̅) + s(-5j̅ – k̅ – i̅ + 2j̅ – 5k̅) + t(-3i̅ + 5j̅ – i̅ + 2j̅ – 5k̅)
= i̅ – 2j̅ + 5k̅ + s(-i̅ – 3j̅ – 6k̅) + t(-4i̅ + 7j̅ – 5k̅)

Question 6.
Find the vector equation of the plane passing through the points (0,0, 0), (0, 5, 0) and (2, 0, 1). (V.S.A)

Answer:
The vector equation of the plane through a, b,c is
r̅ = (1 – s – t)a̅ + sb̅ + tc̅ where s, t ∈ R
⇒ r̅ = (1 – s – t) 0 + s(5j̅) + t(2i̅ + k̅)
= (5s) j̅ + t(2i̅ + k̅);s, t ∈ R

II.
Question 1.
If a, b, c are noncoplanar find the point of intersection of the line passing through the points 2a̅ + 3b̅ – c̅, 3a̅ + 4b̅ – 2c̅ with the line joining points a̅ – 2b̅ + 3c̅, a̅ – 6b̅ + 6c̅. (S.A)

Answer:
The vector equation of the straight line passing through the points 2a̅ + 3b̅ – c̅ and 3a̅ + 4b̅ – 2c̅ is
r̅ = (1 – t) (2a̅ + 3b̅ – c̅) + t(3a̅ + 4b̅ – 2c̅) where t ∈ 1
⇒ r̅ = (2 + t)a̅ + (3 + t) b̅ + (-1 – t)c̅
= (2a̅ + 3b̅ – c̅) + t (a̅ + b̅ – c̅) ……………(1)
The vector equation of the straight line passing through the points a̅ – 2b̅ + 3c̅ and a̅ – 6b̅ + 6c̅ is
r̅ = (a̅ – 2b̅ + 3c̅) (1 – s) + s (a̅ – 6b̅ + 6c̅) where s ∈ R
⇒ r̅ = a̅ + (-2 – 4s) b̅ + (3 + 3s)c̅
= (a̅ – 2b̅ + 3c̅) + s (-4b̅ + 3c̅) …………..(2)
Equating coefficients a̅, b̅, c̅ in (1) and (2) we have
2 + t = 1 ………..(3)
3 + t = – 2 – 4s ……….(4)
and – 1 – t = 3 + 3s ………..(5)
Solving equations (3), (4) and (5) we get t = – 1, and s = – 1
Hence from (1) and (2) the point of intersection of lines (1) and (2) is a̅ + 2b̅
Also line (1) is parallel to a + b – c ancl (2) is parallel to -4b̅ + 3c̅
If a̅ + b̅ – c̅ and 3c̅ – 4b̅ are parallel then two lines are same since they have common point otherwise they have only one point of intersection a̅ + 2b̅

Question 2.
ABCD is a trapezium in which AB and CD are parallel. Prove by vector methods that the mid points of the sides AB, CD and the intersection of the diagonals are collinear. (E.Q)

Answer:
Let A be the origin and $\overline{\mathrm{AB}}$ = b̅
∴ $\overline{\mathrm{DC}}$ = sb̅ (∵ $\overline{\mathrm{DC}} \| \overline{\mathrm{AB}}$)
$\overline{\mathrm{DC}}$ = c̅ – d̅ = sb
⇒ d̅ = c̅ – sb̅
⇒ c̅ – d̅ = sb̅

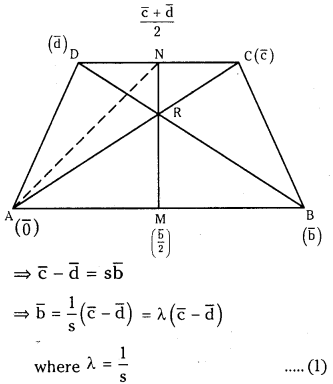
Equation of diagonal AC is
r̅ = (1 – t)o + tc̅
= tc̅ for t ∈ R …………..(2)
Equation of diagonal BD is
r̅ = (1 – s)b̅ + sd̅ for s ∈ R …………(3)

Let R be the point of intersection of diagonals AC and BD.
From (2) and (3) t c = (1 – s) b̅ + s d̅
⇒ t c̅ = (1 – s) b̅ + s (c – sb̅) from (1)
⇒ tc̅ = (1 – s)λ (c – d̅) + sd̅
= (1 – s) λc̅ – [λ(1 – s) – s]d̅
Equating coefficients of c̅ and d̅ on both sides
t = (1 – s) λ and λ (1 – s) – s = 0
⇒ s = λ (1 – s)
⇒ s(1 + λ) = λ
⇒ s = $\frac{\lambda}{1+\lambda}$
∴ t = (1 – s)λ = (1 – $\frac{\lambda}{1+\lambda}$)λ
= $\frac{\lambda}{1+\lambda}$
Position vector of the point of intersection ‘R’ is

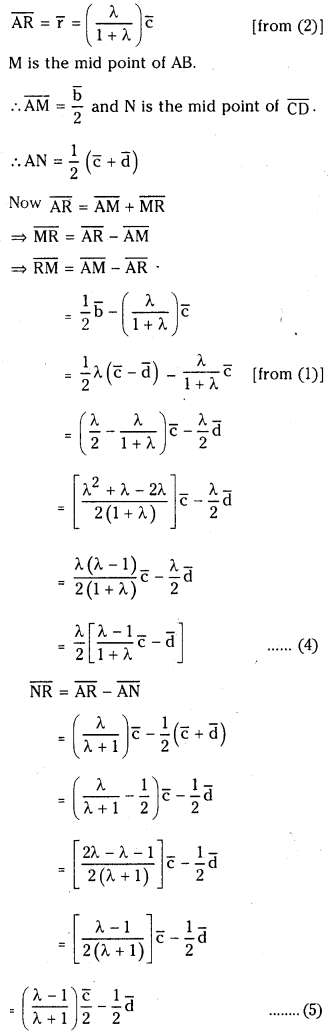
From (4) and (5)
$\overline{\mathrm{RM}}$ = λ $\overline{\mathrm{NR}}$
⇒ M, R, N are collinear.
So the mid points of parallel sides of a trapezium and the point of intersection of the diagonals are collinear.

Question 3.
In a quadrilateral ABCD, if the midpoints of one pair of opposite sides and the point of intersection of the diagonals are collinear, using vector methods, prove that the quadrilateral ABCD is a trapezium. (S.A)

Answer:

$\overline{\mathrm{AB}}=\overline{\mathrm{b}}, \overline{\mathrm{AC}}=\overline{\mathrm{c}}$ and $\overline{\mathrm{AD}}=\overline{\mathrm{d}}$
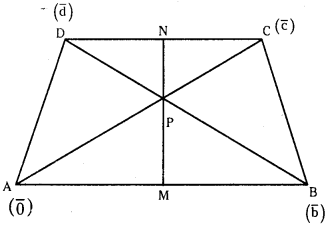
Let M, N be the mid points of one pair of opposite sides AB and CD of a quadrilateral ABCD.
$\overline{\mathrm{AM}}=\frac{\overline{\mathrm{b}}}{2}$
$\overline{\mathrm{AN}}=\frac{\overline{\mathrm{c}}+\overline{\mathrm{d}}}{2}$
Let P be the point of intersection of mid points of sides AB, CD and pair of diagonals AC, BD respectively.
Let $\overline{\mathrm{AP}}=\overline{\mathrm{r}}$. Then equation of $\overline{\mathrm{AC}}$ is
r̅ = t c̅ where t is a scalar ………….(1)
Equation of BD is
r̅ = (1 – s)b̅ + sd̅ for some scalars ………..(2)
and equation of line MN is
r̅ = (1 – α)$\frac{\bar{b}}{2}$ + α$\left(\frac{\bar{c}+\bar{d}}{2}\right)$
where α is a scalar
⇒ 2r̅ = (1 – α)b̅ + a(c̅ + d̅)
⇒ r̅ + r̅ = (1 – α)b̅ + a(c̅ + d̅)
From (1) and (2)
tc̅ + (1 – s)b̅ + sd̅ = (1 – α)b̅ + α(c̅ + d̅)
Equating coefficients of b, c, d we get
1 – s = 1 – oc ⇒ s = a and .
t = a ⇒ s = t = a
From (1) and (2),
t c̅ = (1 – s) b̅ + s d̅
⇒ sc̅ = (1 – s) b̅ + s d̅ (‘- t = s)
⇒ (1 -s) b̅ =s(c̅ – d̅)
⇒ b is parallel to c̅ – d̅
⇒ AB is parallel to CD
∴ ABCD is a trapezium.

III.
Question 1.
Find the vector equation of the plane which passes through the points 2i̅ + 4j̅ + 2k̅, 2i̅ + 3j̅ + 5k̅ and parallel to the vector 3 i̅ – 2 j̅ + k̅. Also find the point where this plane meets the line joining the points 2 i̅ + j̅ + 3k̅ and 4 i̅ – 2 j̅ + 3k̅. (March 2012) (E.Q)

Answer:
Vector equation of the plane which passes through the points a̅ = 2i̅ + 4j̅ + 2k̅, b̅ = 2i̅ + 3j̅ + 5k̅ and parallel to vector c̅ = 3i̅ – 2j̅ + k̅ is
r̅ = (1 – t)a̅ + tb̅ + sc̅ where t, s e R
⇒ r̅ = (1 – t) (2i̅ + 4j̅ + 2k̅) + t(2i̅ + 3j̅ + 5k̅) + s(3i̅ – 2j̅ + k̅)
⇒ r̅ = (2 – 2t + 2t + 3s) i̅ + (4 – 4t + 3t – 2s) j̅ + (2 – 2t + 5t + s) k̅
⇒ r̅ = (2 – 2t + 2t + 3s) i̅ + (4 – 4t + 3t – 2s) j̅ + (2 – 2t + 5t + s) k̅
⇒ r̅ = (2 + 3s) i̅ + (4 – t – 2s) j̅ + (2 + 3t + s)k̅ …………(1)
Vector equation of the line passing through the points c̅ = 2i̅ + j̅ + 3k̅ and d̅ = 4 i̅ – 2 j̅ + 3k̅ is r̅ = (1 – a)d̅ + ac̅ where a e R
⇒ r̅ = (1 – α)(2i̅ + j̅ + 3k̅) + α(4i̅ – 2j̅ + 3k̅)
⇒ r̅ = (2 – 2α + 4α) i̅ + (1 – α – 2α) j̅ + (3 – 3α + 3α)k̅
⇒ r̅ = (2 + 2α) i̅ + (1 – 3α) j̅ + 3k̅ (2)
Let 7 be the point of intersection of (1) and (2)
(2 + 3s)i̅ + (4 – t – 2s) j̅ + (2 + 3t + s) k̅
= (2 + 2α) i̅ + (1 – 3α) j̅ + 3k̅
v Since i̅, j̅, k̅ are non coplanar,
2 + 3s = 2 + 2α ⇒ 2α – 3s = 0 ………………(3)
4 – 1 – 2s = 1 – 3α ⇒ 3α – 2s -1 = – 3 …………(4)
2 + 3t + s = 3 ⇒ s + 3t = 1 ………………(5)
From (5), t = $\frac{1-\mathrm{s}}{3}$
∴ From (4) 3α – 2s – $\left(\frac{1-s}{3}\right)$ = -3
⇒ 9α – 6s – 1 + s = -9
9α – 5s + 8 = 0 (6)
Solving (6) & (3) equations

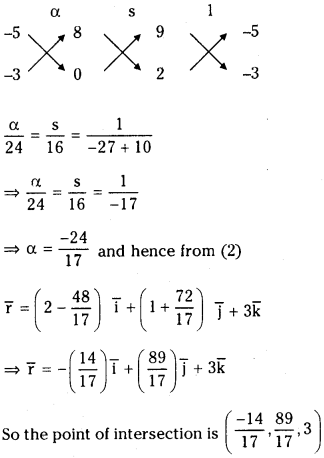
Question 2.
Find the vector equation of the plane passing through the points 4 i̅ – 3 j̅ – k̅ , 3i̅ + 7j̅ – 10k̅ and 2i̅ + 5j̅ – 7k̅ and show that the point i̅ + 2 j̅ – 3k̅ lies in the plane. (March 2013) (S.A.Q.)

Answer:
Vector equation of the plane passing through
A(4i̅ – 3j̅ – k̅ ), B (3i̅ + 7j̅ – 10k̅ ) and C(2i̅ + 5j̅ – 7k̅ ) is
r̅ = (1 – s – t) (4i̅ – 3 j̅ – k̅ ) + s(3i̅ + 7j̅ – 10k̅ ) + t(2i̅ + 5j̅ – 7k̅ )
Let D (i̅ + 2j̅ – 3k̅ ) lies on the plane, then
(i̅ + 2j̅ – 3k̅ ) = (1 – s – t)(4i̅ – 3j̅ – k̅ ) + s (3i̅ + 7j̅ – 10k̅ ) + t (2i̅ + 5j̅ – 7k̅ )
Since i̅ , j̅ ,k̅ are non coplanar, equating coefficients of i̅ , j̅ , k̅ both sides.
4(1 – s – t) + 3s + 2t = 1
⇒ 4 – 4s – 4t + 3s + 2t = 1
⇒ s + 2t = 3 …………(1)
– 3 (1 – s – t) + 7s + 5t = 2
⇒ -3 + 3s + 3t + 7s + 5t = 2
⇒ 10s + 8t = 5
Also – (1 – s – t) – 10s – 7t = – 3
⇒ – 1 + s + t – 10s – 7t = – 3
⇒ 9s + 6t = 2
From (1), 3s + 6t = 9
Solving (1) & (3) equations 6s = – 7
⇒ s = – 7/6

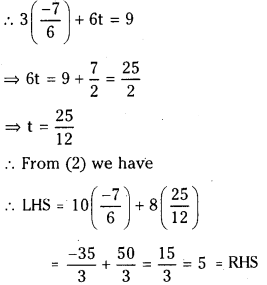
s = $\frac{-7}{6}$ t = $\frac{25}{12}$. satisfy (1), (2), (3).
and D lies on the plane passing through A, B, C.