Microorganisms Friend and Foe
Microorganisms Friend and Foe
NCERT TEXTBOOK EXERCISES
Question 1.
Fill in the blanks.
- Microorganisms can be seen with the help of a………………
- Blue-green algae fix………….. directly from the air and enhance the fertility of the soil.
- Alcohol is produced with the help of……………….
- Cholera is caused by………………….
Answer.
- microscope
- nitrogen
- yeast
- bacteria.
Question 2.
Tick the correct answer.
(a) Yeast is used in the production of
- (i) sugar
- (ii) alcohol
- (iii) hydrochloric acid
- (iv) oxygen
Answer.
(ii) alcohol
(b) The following is an antibiotic
- (i) Sodium bicarbonate
- (ii) Streptomycin
- (iii) Alcohol
- (iv) Yeast
Answer.
(ii) Streptomycin
(c) Carrier of malaria-causing protozoan is
- (i) female Anopheles mosquito
- (ii) cockroach
- (iii) housefly
- (iv) butterfly
Answer.
(i) female Anopheles mosquito
(d) The most common carrier of communicable diseases is
- (i) ant
- (ii) housefly
- (iii) dragonfly
- (iv) spider
Answer.
(ii) housefly
(e) The bread or idli dough rises because of
- (i) heat
- (ii) grinding
- (iii) growth of yeast cells
- (iv) kneading
Answer.
(iii) growth of yeast cells
(f) The process of conversion of sugar into alcohol is called
- (i) nitrogen fixation
- (ii) moulding
- (iii) fermentation
- (iv) infection
Answer.
(iii) fermentation.
Question 3.
Match the organisms in Column A with their action in Column B.
| Column A |
Column B |
|
(i) Bacteria
(ii) Rhizobium
(iii) Lactobacillus
(iv)Yeast
(v) A protozoan
(vi) A virus
|
(a) Fixing nitrogen
(b) Setting of curd
(c) Baking of bread
(d) Causing malaria
(e) Causing cholera
(f) Causing AIDS
(g) Producing antibodies
|
Answer.
| Column A |
Column B |
| (i) Bacteria |
(e) Causing cholera |
| (ii) Rhizobium |
(a) Fixing nitrogen |
| (iii) Lactobacillus |
(b) Setting of curd |
| (iv) Yeast |
(c) Baking of bread |
| (v) A protozoan |
(d) Causing malaria |
| (vi) A virus |
(f) Causing AIDS |
Question 4.
Can microorganisms be seen with the naked eye? If not, how can they be seen?
Answer.
No, we cannot see microorganisms with unaided eyes. They can be seen with the help of a microscope.
Question 5.
What are the major groups of microorganisms?
Answer.
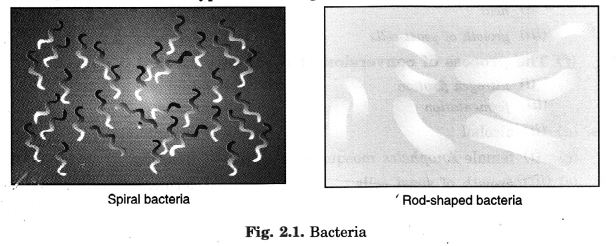
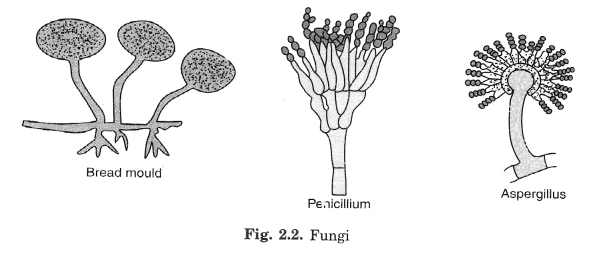
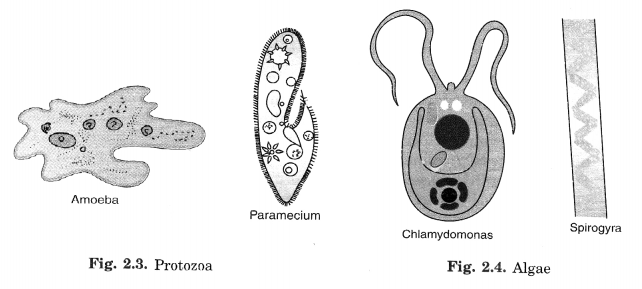
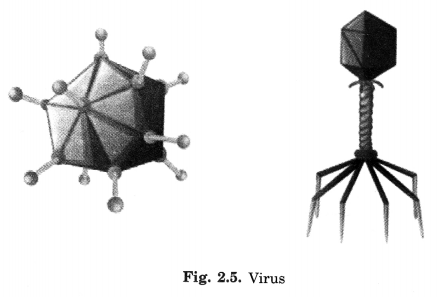
Microorganisms are classified into four major groups based on their size. These are:
- Bacteria
- Fungi
- Protozoa
- Some algae.
Viruses are another type of microorganisms.
Question 6.
Name the microorganisms which can fix atmospheric nitrogen in the soil.
Answer.
They are
- Rhizobium
- Azobhcter
- blue-green algae (such as Anabaena and Nostoc), etc..
Question 7.
Write 10 lines on the usefulness of microorganisms in our lives.
Answer.
Microorganisms are useful for us in many ways e.g.,
- the bacterium, lactobacillus converts milk into curd.
- bacteria are also involved in the making of cheese.
- Acetobacter acetic is used for the production of acetic acid from alcohol.
- Yeast is used for the commercial production of alcohol and wine.
- Antibiotics are manufactured by growing specific microorganisms.
- Some bacteria fix atmospheric nitrogen and increase soil fertility.
- Bacteria are used in the preparation of medicines like antibiotics and vaccines.
- Bacteria are used in the preservation of pickles and many other food items.
- Yeast is also used in the baking industry for making bread, pastries, and cakes.
- They act as cleansing agents and decompose the waste products into manure.
Question 8.
Write a short paragraph on the harmful effects of microorganisms.
Answer.
The harms caused by microorganisms are as follows:
- Many communicable diseases, such as cholera, common cold, chickenpox, tuberculosis, etc., are caused by microorganisms.
- Malaria is caused by a microorganism called Plasmodium carried by the female Anopheles mosquito.
- The Female Aedes mosquito acts as a carrier of the dengue virus.
- Anthrax is a dangerous human and cattle disease caused by a bacterium called Bacillus anthracis.
- Several microorganisms cause diseases in plants like wheat, rice, potato, sugarcane, orange, apple, etc., and reduce the yield of the crops.
- Food poisoning is also caused by microorganisms. They make food poisonous by producing toxic substances in the food.
Question 9.
What are antibiotics? What precautions must be taken while taking antibiotics?
Answer.
The medicines, that kill or stop the growth of the disease-causing microorganisms, are called antibiotics. Streptomycin, tetracycline, erythromycin, etc. are some of the commonly known antibiotics which are made from fungi and bacteria.
The precautions to be taken while taking antibiotics are as follows :
- These medicines should be taken only on the advice of a qualified doctor.
- One must complete the course prescribed by the doctor.
- If anybody takes antibiotics when not needed, his/her body may develop resistance against that antibiotic.